Envision Geometry Answer Key for Quick Solutions

Understanding complex mathematical problems can be a challenge for many learners. Accessing reliable resources that provide accurate solutions is essential to improving problem-solving skills and boosting confidence. Whether you are working through homework assignments or preparing for exams, the right materials can make a significant difference in your performance.

Effective study tools offer clear, step-by-step solutions that help students grasp important concepts and enhance their understanding of difficult topics. By referring to trusted materials, learners can check their work, correct errors, and gain insights into various solving techniques. This process not only aids in completing exercises but also promotes deeper learning and retention of key principles.

Step-by-step guides allow students to track their progress and refine their problem-solving approaches. With consistent practice and the right guidance, overcoming even the most challenging tasks becomes more manageable. Whether for quick reference or in-depth study, the correct support is crucial in achieving academic success in mathematics.

Envision Geometry Answer Key Overview

For students seeking assistance with their mathematical assignments, accessing reliable resources that offer accurate solutions is crucial. These tools provide a systematic breakdown of problems, helping learners comprehend the steps involved in reaching the correct results. Whether tackling complex equations or reviewing basic concepts, having the right solutions at hand can clarify doubts and reinforce understanding.

Importance of Step-by-Step Guides

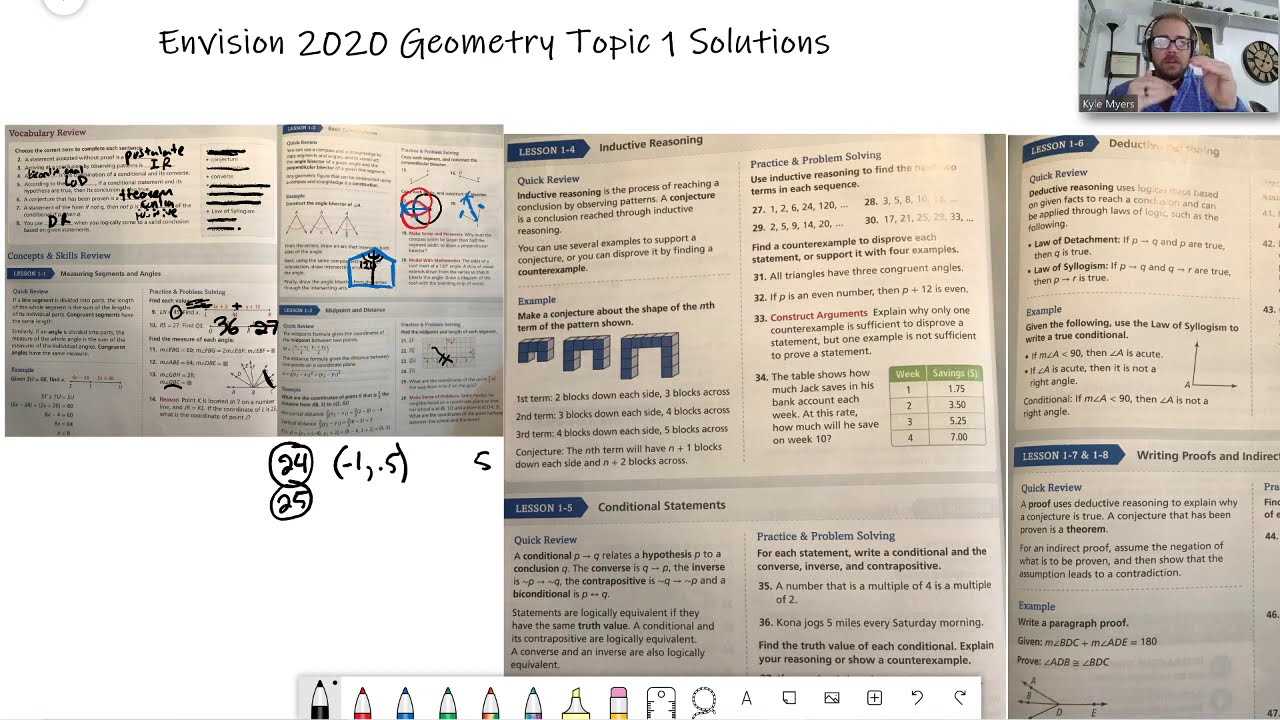
Providing clear instructions for each problem allows students to follow the correct approach. Step-by-step solutions not only show the final answer but also explain how to reach it, highlighting essential techniques and strategies along the way. This approach fosters deeper understanding and enables learners to apply similar methods to other problems independently.

Utilizing Resources for Effective Learning

When used correctly, these resources serve as valuable learning aids, helping students identify mistakes and correct them. They offer more than just solutions; they guide users through the problem-solving process, building critical thinking skills that extend beyond the classroom. With consistent use, students can gain confidence and improve their mathematical proficiency.

How to Use Envision Geometry Answers

To effectively utilize problem-solving resources, it’s essential to follow a structured approach. These materials are designed to guide students through each step of the process, ensuring they understand how to reach the correct conclusions. Below are several strategies to make the most out of these tools:

Start with the basics: Before jumping to the solutions, carefully review the problem to identify what is being asked. Make sure you understand the key concepts involved.
Follow step-by-step instructions: Carefully study each step provided in the solution guide. These instructions are designed to help you understand the reasoning behind each calculation and technique.
Check your work: After completing the steps on your own, compare your results with the provided solutions. If there are discrepancies, analyze the steps to find where the error occurred.
Learn from mistakes: If you find that your answer is incorrect, use the resource to pinpoint the exact mistake and correct it. This process helps reinforce learning and improves problem-solving skills.
Practice regularly: The more you practice with these materials, the more confident you will become in your ability to tackle similar problems independently.

By incorporating these steps into your study routine, you can build a strong foundation and improve your ability to solve problems effectively and accurately.

Benefits of Accurate Answer Keys

Having reliable resources that provide correct solutions is essential for effective learning. When students have access to precise solutions, they are better equipped to identify their mistakes, understand the steps involved, and improve their problem-solving abilities. These tools serve as an invaluable guide for both self-study and homework review.

Enhanced Learning and Understanding: Accurate solutions not only provide the right answer but also offer detailed explanations of the process. This helps learners understand the logic behind each step, making complex concepts easier to grasp and apply in future problems.

Boosted Confidence: When students are able to verify their work and see that their methods align with the correct solutions, it builds confidence. This reassurance encourages them to tackle more difficult problems with a greater sense of assurance.

Efficient Problem-Solving: By referring to well-structured resources, learners can avoid time-consuming errors. This efficiency allows them to solve problems more quickly, which is especially beneficial during exams or when managing multiple assignments.

Identification of Mistakes: Mistakes are an inevitable part of the learning process. Accessing accurate resources enables students to pinpoint errors, understand why they occurred, and learn how to avoid them in the future.

Common Geometry Questions Explained

Many students encounter recurring challenges when solving mathematical problems, especially in areas involving shapes, measurements, and spatial reasoning. Addressing these common questions helps to build a clearer understanding and improves overall problem-solving skills. Below are some frequently asked questions and their solutions, which can help clarify key concepts and provide guidance.

How to Calculate the Area of Shapes

One of the most common areas of confusion is determining the area of various shapes. The formulas vary depending on the type of figure, but understanding the principles behind them is crucial for solving problems quickly and accurately.

Rectangle: Multiply length by width.
Triangle: Multiply the base by the height, then divide by two.
Circle: Multiply pi by the square of the radius.

Understanding Angles and Their Properties

Another frequent question revolves around angles–specifically how to find unknown angles in different types of shapes, such as polygons or circles. Here are some general rules that can help:

Sum of interior angles in a polygon: The sum of the interior angles of a polygon is given by the formula (n-2) × 180°, where n is the number of sides.
Complementary and supplementary angles: Complementary angles add up to 90°, and supplementary angles add up to 180°.
Angles in a circle: The total of all angles around a point is 360°.

Understanding these basic principles provides a solid foundation for solving more complex problems involving angles and shapes. By practicing these calculations and strategies, learners can increase their confidence and ability to tackle similar questions in the future.

Step-by-Step Solutions for Homework

When tackling assignments, it’s essential to break down each problem into smaller, manageable steps. This method ensures clarity and reduces the risk of errors. By following a structured approach, students can effectively solve complex questions, gaining a deeper understanding of the material in the process. Below is an example of how to approach problems using detailed, methodical solutions.

Step 1: Read the Problem Carefully – Before starting any calculations or operations, make sure to fully understand the problem. Identify the key information and what needs to be solved. Pay attention to units, values, and any additional instructions provided.

Step 2: Organize the Information – Once the problem is understood, organize the given data. Write down the known values and identify what needs to be found. This will help in visualizing the steps ahead and ensure you don’t miss any important details.

Step 3: Apply Relevant Formulas – Use the appropriate formulas or methods needed to solve the problem. This could involve applying basic arithmetic, algebraic operations, or more advanced techniques, depending on the task.

Step 4: Solve Step-by-Step – Work through each part of the problem slowly and carefully. Avoid skipping steps, as each one is important for ensuring the final result is correct. If you encounter any obstacles, review previous steps to check for mistakes.

Step 5: Verify the Solution – After obtaining the final result, take a moment to double-check your work. Ensure that the units are correct, the calculations are accurate, and that the solution makes sense in the context of the problem.

By following these steps for each homework question, students will improve their problem-solving skills and achieve greater success in completing assignments.

Understanding Geometry Concepts through Answers

Grasping fundamental concepts in mathematics becomes easier when students can review how each step of a problem is solved. By following through with well-explained solutions, learners can uncover the logic behind key concepts and learn the techniques required to apply them in different contexts. This process is essential for building a solid foundation and progressing to more complex topics.

Breaking Down Complex Problems

In many cases, mathematical problems can seem overwhelming at first. However, when solutions are broken down step-by-step, the process becomes much clearer. Each phase of the solution builds upon the previous one, revealing how concepts such as shapes, angles, and measurements work together to form a complete understanding.

Identifying key components: Before diving into solving, understanding what each part of the problem represents helps clarify what is being asked.
Using foundational principles: Many complex problems rely on basic concepts that can be applied in multiple situations. Recognizing these allows for faster, more accurate solutions.

How Solutions Help in Concept Retention

By reviewing correct solutions, students reinforce their learning and enhance retention. Understanding why a particular method or formula is used in each instance ensures that similar problems can be solved independently in the future. This repeated exposure to logical problem-solving also improves critical thinking and strengthens mathematical intuition.

How Envision Geometry Helps Students Learn

Educational resources that provide clear, step-by-step solutions play a key role in helping students understand complex mathematical concepts. These tools not only show the correct answers but also guide learners through the problem-solving process, enabling them to see the logic and reasoning behind each step. This method supports students in developing critical thinking skills and improving their ability to approach similar problems in the future.

Fostering a Deeper Understanding: When students have access to structured solutions, they can connect abstract concepts to practical applications. By following detailed explanations, they gain insight into why specific formulas or techniques are used, which deepens their understanding and enhances retention of the material.

Encouraging Independent Problem-Solving: With the guidance of these resources, students learn how to break down problems into manageable parts. This approach not only boosts their confidence but also encourages independent thinking. Over time, as students apply these techniques to new challenges, they become more capable of solving problems on their own.

Building Confidence and Mastery: As students work through problems and compare their methods with provided solutions, they develop a sense of accomplishment. The ability to verify their work and understand where they went wrong helps build confidence, turning challenges into learning opportunities.

Why Answer Keys are Essential for Success

Having access to comprehensive solutions is critical in the learning process, especially when tackling complex subjects. These resources not only provide the correct results but also show the reasoning behind each step. This approach enables learners to understand the methodology used and helps them apply the same principles to similar problems in the future. The ability to check and verify solutions fosters confidence and reinforces learning, making it an essential tool for academic success.

Understanding Mistakes and Correcting Them

One of the main benefits of using detailed solutions is the opportunity it provides to learn from mistakes. When students can compare their work with the correct methods, they can pinpoint where they went wrong and understand why a particular approach is more effective. This process promotes deeper learning and helps avoid repeating the same errors in the future.

Clarifying concepts: Checking solutions helps students better grasp complex ideas by showing them how each step connects.
Building problem-solving skills: By analyzing the steps taken in a solution, students improve their ability to break down problems systematically.

Boosting Confidence and Independence

When students have access to reliable solutions, they can approach their work with more confidence. They are more likely to attempt challenging problems, knowing that they can verify their progress and ensure accuracy. Over time, this helps build independence as students become more comfortable solving problems on their own.

Reinforcing knowledge: Regularly reviewing solutions boosts retention of key concepts and improves overall understanding.
Developing critical thinking: By evaluating and applying solutions, students develop better reasoning skills that extend beyond the subject at hand.

Exploring Geometry Solution Guide Features

Comprehensive solution guides provide a range of valuable features designed to support students in mastering mathematical concepts. These resources are structured to break down complex problems into clear, manageable steps, making it easier for learners to follow along and grasp the underlying principles. From detailed explanations to visual aids, these guides offer a variety of tools that help strengthen problem-solving skills and enhance understanding.

Step-by-Step Breakdown

One of the standout features of these resources is the step-by-step breakdown of each problem. This structured approach allows students to see how to approach a problem methodically, ensuring that they understand each part of the process. Whether it involves identifying key components or applying specific formulas, each stage is explained in detail.

Clarity: Each solution is explained in a straightforward, easy-to-follow manner.
Comprehensive details: No step is left out, helping students avoid confusion and make connections between concepts.

Visual Aids and Examples

Visual aids, such as diagrams and graphs, play a crucial role in helping students visualize mathematical concepts. These tools make abstract ideas more tangible and easier to comprehend. By combining text explanations with visual representations, learners can see how theoretical concepts are applied in practice, which aids in their retention and understanding.

Diagrams: Diagrams help students visualize geometric shapes and relationships, making abstract concepts more accessible.
Worked-out examples: Examples show how to apply the learned techniques to new problems, reinforcing the methods in practice.

Encouraging Independent Learning: With these features, students are better equipped to solve problems on their own, as they can refer to the solutions for guidance and build confidence in their abilities. The combination of detailed instructions, visual aids, and comprehensive examples fosters a deeper understanding and empowers students to approach new challenges with greater ease.

Tips for Effective Geometry Study

Mastering mathematical subjects requires a combination of consistent practice, clear understanding, and strategic learning techniques. To succeed, it’s essential to break down complex problems, reinforce concepts through regular practice, and apply critical thinking to each task. By following a structured approach to studying, students can enhance their problem-solving abilities and achieve better results in their coursework.

Break Down Complex Problems

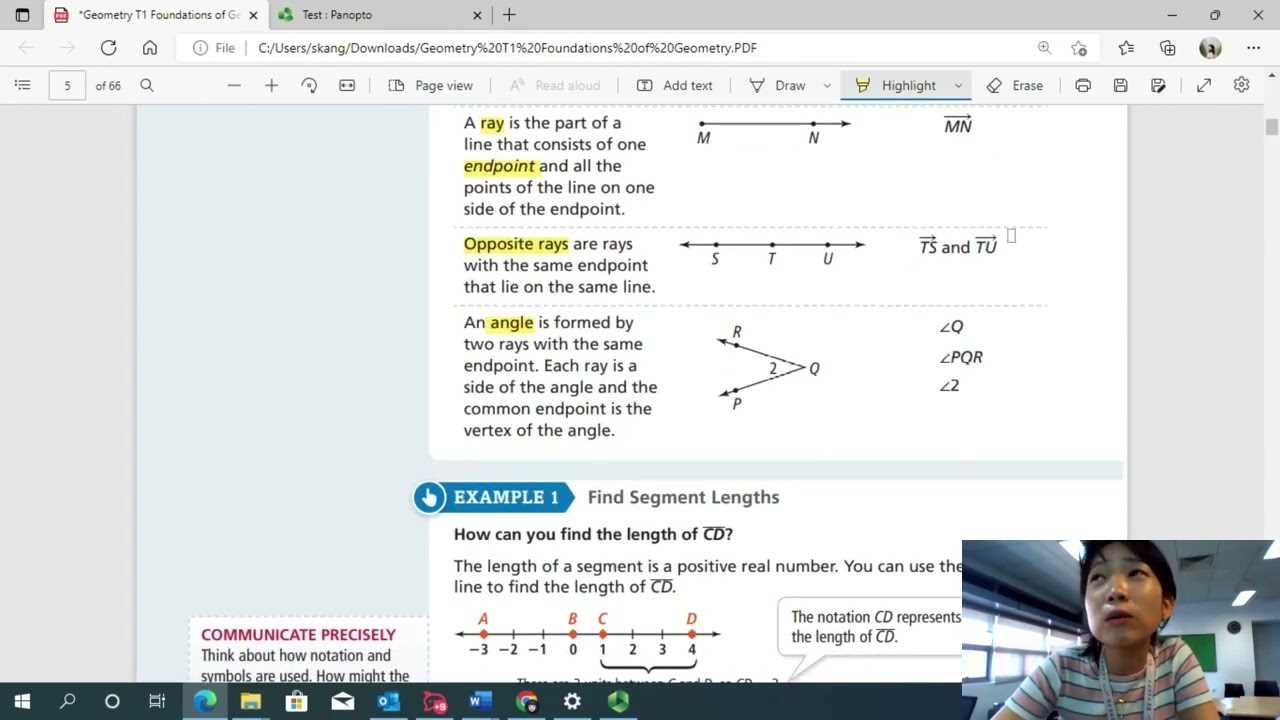
One of the most effective study techniques is breaking down difficult problems into smaller, manageable parts. This approach not only makes the task seem less overwhelming but also allows for a clearer understanding of each individual step. As you work through each component, you’ll gain a better grasp of the larger picture and improve your ability to handle more complex problems.

Focus on one concept at a time: Isolate individual topics to fully grasp the material before moving on.
Work through examples: Practice with solved problems to see how each step is executed before attempting similar tasks on your own.

Review and Reinforce Key Concepts

Regular review of key concepts is essential to long-term retention. The more frequently you revisit important formulas, methods, and techniques, the more solid your foundation will become. Utilize various resources, such as practice worksheets, guides, and visual aids, to reinforce these ideas and ensure a deeper understanding.

Use visual aids: Diagrams and charts can help clarify abstract concepts and make them easier to remember.
Practice consistently: Regularly solving problems helps strengthen your grasp of the material and improves your ability to recall solutions under pressure.

Stay Consistent and Focused: Success in any subject, especially one as challenging as mathematics, requires consistent effort and concentration. By creating a study schedule and sticking to it, students can maintain steady progress and avoid last-minute cramming. With the right approach, every problem becomes an opportunity to learn and grow.

Key Geometry Topics Covered in Envision

In any comprehensive math curriculum, certain fundamental topics serve as the foundation for a deeper understanding of the subject. These essential areas are introduced progressively, allowing students to build upon their knowledge. The following table outlines the key topics typically covered, helping students focus on the most important concepts and prepare for more advanced material.

Topic	Description
Angles and Their Properties	Understanding different types of angles (acute, obtuse, right) and how they relate to one another.
Shapes and Figures	Study of various two- and three-dimensional shapes, including their properties and measurements.
Area and Perimeter	Learning how to calculate the area and perimeter of different shapes like squares, triangles, and circles.
Congruence and Similarity	Exploring the conditions under which two shapes are congruent or similar, and applying those principles to solve problems.
Pythagorean Theorem	A key theorem used to solve problems involving right-angled triangles, connecting the lengths of the sides.
Transformations	Understanding geometric transformations such as translations, rotations, reflections, and dilations.
Volume and Surface Area	Calculating the volume and surface area of three-dimensional shapes such as cubes, spheres, and pyramids.
Coordinate Geometry	Working with coordinates and graphing points, lines, and curves to solve geometric problems.

Each of these topics builds on the previous one, providing students with a structured approach to mastering key mathematical concepts. By focusing on these core areas, learners develop a deeper understanding that can be applied to more complex scenarios in both academic and real-world situations.

How to Find the Right Answer Guide

When tackling mathematical problems, having access to the right solution guide is essential for understanding the material and improving problem-solving skills. Finding a reliable resource can help verify answers, clarify concepts, and guide students through complex steps. However, it’s crucial to ensure that the guide you use aligns with the content you are studying and helps you learn effectively.

Check the Source of the Guide

One of the most important factors in selecting the right solution guide is the source. Reliable materials often come from trusted educational publishers, academic websites, or teachers who are experts in the subject. Be sure to verify the credibility of the guide to ensure that it is accurate and up-to-date with current curriculum standards.

Look for reputable educational sites: These resources often provide verified solutions and clear explanations.
Check with instructors: Teachers can often recommend the best guides that align with the course content.

Ensure It Matches Your Curriculum

Not all solution guides are created equal, and not all of them will address the specific topics you are studying. It’s essential to choose one that matches the content of your lessons. This will ensure that the solutions provided are relevant and that the explanations are applicable to the exercises you need help with.

Review the topics covered: Make sure the guide includes the areas you’re studying in class.
Look for step-by-step solutions: Guides that break down each problem into manageable steps can be especially helpful for understanding the methodology.

By choosing the right solution guide, students can enhance their understanding of the subject and improve their ability to solve complex problems independently.

Common Mistakes in Geometry Solving

Mathematical problem-solving can be challenging, especially when dealing with concepts that require both analytical thinking and spatial reasoning. While working through problems, students often encounter common errors that can hinder their progress. Recognizing these mistakes is the first step toward improving problem-solving skills and achieving better results.

Misinterpreting the Problem Statement

One of the most frequent mistakes is misunderstanding the problem itself. Sometimes, the wording of a question can be confusing, leading to incorrect assumptions about what is being asked. It’s important to carefully read each problem and identify the key information, such as given values, unknowns, and relationships between geometric elements.

Take time to analyze the problem: Read the question multiple times to ensure that all details are understood.
Highlight key terms: Mark important pieces of information that will guide your solution.

Forgetting to Apply Necessary Theorems

In many cases, students fail to apply essential geometric principles or theorems, leading to incomplete or incorrect solutions. Whether it’s the Pythagorean theorem, properties of angles, or rules about shapes, neglecting these important tools can result in errors. It’s crucial to remember and use the correct formulas or reasoning steps to solve the problem accurately.

Review key theorems: Make sure you are familiar with the most relevant formulas for the specific problem.
Apply theorems systematically: Ensure each step follows logically from the previous one to avoid skipping essential calculations.

Overlooking Units of Measurement

Another common mistake is neglecting to account for units when solving problems. Whether dealing with lengths, areas, or volumes, it’s important to keep track of the units used in the problem and ensure that the final answer is expressed correctly. Failure to do so can lead to miscalculations and incorrect results.

Check units regularly: Pay attention to the units given in the problem and make sure they match your final answer.
Convert units when necessary: If the problem requires converting between different units, do so carefully to avoid mistakes.

By being aware of these common pitfalls and actively working to avoid them, students can improve their understanding and problem-solving skills, leading to more successful results in mathematical tasks.

Why Accuracy Matters in Geometry Answers

In any mathematical discipline, precision is essential. In the context of spatial reasoning and mathematical problem solving, even a small mistake can lead to significantly incorrect results. Whether it’s calculating dimensions, areas, or volumes, ensuring the accuracy of each step is critical to achieving the correct solution.

Accurate solutions not only reflect a student’s understanding but also help in building a solid foundation for more advanced concepts. Each geometric figure, angle, or equation follows a set of logical steps, and errors at any stage can cause confusion, making the learning process harder to navigate.

Impact of Inaccurate Solutions

Incorrect results can have far-reaching consequences, especially when geometric principles are applied in real-life situations such as architecture, engineering, and design. Even a minor miscalculation in dimensions or angles can lead to significant discrepancies, causing costly mistakes. In academic settings, accuracy in solving geometric problems is also vital to maintaining grades and improving overall mathematical proficiency.

How to Ensure Accuracy

To achieve accurate results, one must pay attention to detail and follow systematic methods. Here are some tips for improving precision:

Double-check calculations: Always review each step of the process to identify possible errors.
Understand the concepts: A deep understanding of the underlying principles reduces the chance of making mistakes.
Use tools correctly: Rely on calculators, rulers, or compasses appropriately to ensure accurate measurements.

In conclusion, accuracy is not just important for achieving the correct solution but is also an essential skill that builds mathematical competence and confidence. By prioritizing precision, students can enhance their problem-solving abilities and develop a deeper understanding of mathematical concepts.

How Answer Keys Improve Learning Speed

In any educational process, timely feedback is crucial for faster comprehension and mastery of new material. Having access to solutions allows students to quickly identify mistakes, understand the correct approach, and reinforce their learning. By examining the correct answers and the steps that led to them, students can accelerate their learning process and avoid repeating errors.

Immediate correction of misunderstandings helps in minimizing confusion, giving learners the opportunity to adjust their thinking and improve their problem-solving skills. This process not only aids in mastering the current topic but also builds a foundation for understanding more complex concepts in the future.

Benefits of Using Solutions for Learning Speed

Faster Error Detection: Students can pinpoint mistakes right away and address them before they become ingrained habits.
Clarification of Concepts: Seeing the correct approach helps clarify difficult concepts and methods that might be confusing initially.
Reinforced Learning: Repetition of the correct steps strengthens retention and boosts confidence in solving similar problems.

Effective Use of Solutions for Better Speed

To maximize the learning benefits of solutions, it is essential to use them strategically:

Review after each practice: After attempting a problem, compare your solution to the provided one to see where improvements can be made.
Understand the reasoning: Don’t just memorize the correct solution. Take time to understand the logic behind each step.
Practice consistently: The more you practice with feedback, the faster you will become at identifying and correcting mistakes on your own.

In conclusion, having access to well-organized solutions not only helps students correct errors faster but also enhances their overall learning experience, making the entire process more efficient and rewarding.

Maximizing Your Geometry Study with Answers

To make the most of your study sessions, it’s essential to incorporate solutions as a tool for understanding and reinforcing concepts. Simply attempting problems without feedback can limit your progress. By reviewing solutions, you gain insight into the correct methods and reasoning behind each step. This process not only helps correct mistakes but also strengthens your understanding of the material and speeds up the learning process.

Maximizing your study efficiency means knowing when and how to use provided solutions effectively. It’s not just about finding the right answers, but understanding the path that leads to them. This approach helps you recognize patterns, improve problem-solving techniques, and build confidence in your abilities.

Ultimately, combining practice with the right feedback creates a solid foundation for mastering more complex topics and achieving long-term academic success. Use solutions strategically to optimize your study time and develop a deeper comprehension of the subject.