Eureka Math Grade 3 Module 4 Answer Key

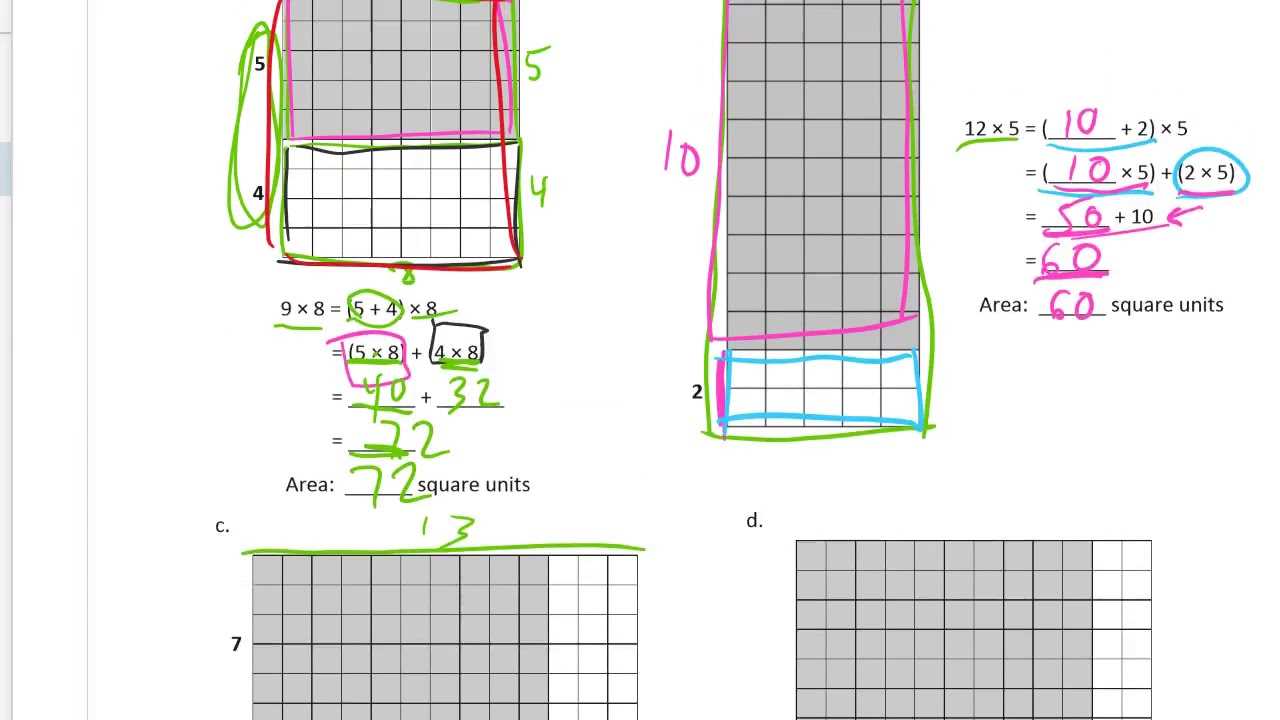
In third grade, students are introduced to more complex concepts that lay the foundation for future learning. As they begin to understand the relationships between numbers and various operations, it’s essential to have a structured approach to mastering these skills. This section provides guidance and explanations that help clarify key topics students encounter throughout their studies.

The focus here is on enhancing problem-solving abilities through practical exercises. Understanding how to approach challenges step-by-step is crucial for building confidence and competence. By following the provided examples and explanations, learners will be able to develop a solid understanding of the material, ensuring better outcomes both in class and at home.

With the right resources and support, students can thrive in this crucial phase of their education. Clear solutions and detailed breakdowns of each topic can make all the difference in simplifying complex ideas and encouraging further exploration of mathematics.

Eureka Math Grade 3 Module 4 Answer Key

This section is designed to provide a comprehensive guide for students and parents working through the core concepts in third-grade mathematics. By offering detailed solutions to the exercises, learners can check their understanding and identify areas where further review may be needed. Clear explanations accompany each solution, ensuring students grasp the essential principles before moving on to more advanced topics.

Step-by-Step Solutions for Key Topics

The exercises in this section cover a wide range of fundamental topics, from basic operations to more complex problem-solving methods. Each problem is broken down into manageable steps, which helps students see how different mathematical concepts are connected. By following the step-by-step breakdown, students can improve their ability to solve similar problems independently.

Additional Tips for Success

While working through the problems, it is important for students to pay close attention to each step. Careful practice and repeated review will build a solid foundation for future learning. Additionally, parents can assist by encouraging their children to explain their thought processes aloud, which reinforces understanding and confidence. With consistent practice, students will find it easier to tackle new challenges and make meaningful progress.

Overview of Eureka Math Module 4

This section focuses on building critical skills necessary for students to understand key number operations and problem-solving strategies. The content aims to strengthen their ability to perform calculations and interpret mathematical information in a structured and meaningful way. The main objective is to equip students with the tools they need to handle more complex concepts and apply them in real-world situations.

Core Concepts Covered

Throughout this section, learners will encounter a variety of important topics designed to enhance their understanding of numbers and relationships. Key concepts include:

• Understanding place value and its significance in arithmetic operations
• Multiplication and division strategies, including the use of arrays and number lines
• Problem-solving approaches for word problems involving basic operations
• Exploring the relationships between different mathematical operations

Application of Skills

The knowledge gained through this unit is crucial for developing a deeper understanding of mathematical concepts. Students will have opportunities to:

1. Practice solving problems with increasing difficulty
2. Apply their skills to real-world scenarios to see how math is used in daily life
3. Reinforce concepts through a variety of interactive exercises and challenges

By mastering these foundational topics, students will be well-prepared to tackle more advanced material in future lessons.

Key Concepts Covered in Module 4

This section introduces fundamental ideas that form the backbone of students’ understanding of numbers and operations. The concepts presented aim to develop critical thinking skills, helping students recognize patterns and relationships between numbers. These principles are essential for solving both simple and complex problems, and they lay the groundwork for more advanced mathematical thinking.

The following table summarizes the key ideas covered in this section:

Concept	Description
Place Value	Understanding the value of each digit in a number based on its position, crucial for performing calculations and comparing numbers.
Multiplication Strategies	Methods for efficiently multiplying numbers, including using arrays and skip counting.
Division Techniques	Learning how to divide numbers by understanding division as the inverse of multiplication.
Word Problems	Applying learned operations to solve real-world scenarios through structured problem-solving methods.

By mastering these essential concepts, students will gain the necessary skills to solve increasingly complex problems with confidence and clarity.

Understanding the Operations in Module 4

This section delves into the essential operations that students need to master in order to build a solid foundation for future learning. By focusing on understanding how different operations work together, students will be able to perform calculations more efficiently and solve problems with greater ease. The goal is to help learners develop a deeper understanding of how numbers interact in various mathematical contexts.

The following table outlines the primary operations covered and their key characteristics:

Operation	Explanation
Addition	The process of combining two or more numbers to find a total, a fundamental concept for solving a wide range of problems.
Subtraction	Removing one quantity from another to determine the difference, often used to compare or find the remainder in real-world scenarios.
Multiplication	A method of adding a number to itself multiple times, an essential skill for working with larger numbers and understanding patterns.
Division	Splitting a number into equal parts or groups, helping to understand how quantities can be distributed or shared equally.

By fully understanding these operations, students can confidently approach more complex problems, applying the right strategies to achieve accurate results.

Step-by-Step Guide for Module 4 Answers

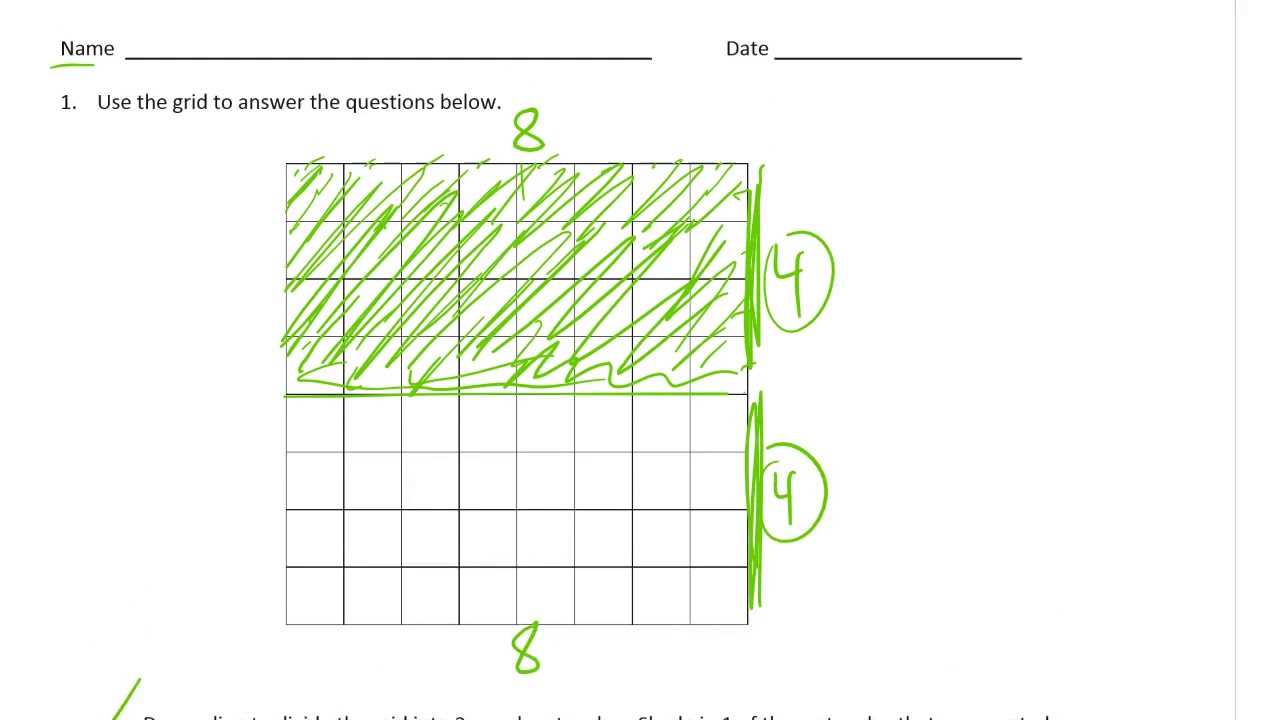
This section offers a detailed walkthrough of how to approach and solve the exercises presented in this section. By breaking down each problem into clear steps, students can follow a logical process to arrive at the correct solutions. The goal is to build confidence in problem-solving and reinforce the understanding of key concepts through practice.

Understanding the Process

Each problem is approached systematically, ensuring that students follow the correct sequence of operations. Below is an outline of the general approach for solving the exercises:

• Step 1: Read the problem carefully and identify the key information.
• Step 2: Determine which operations are required to solve the problem (addition, subtraction, multiplication, division).
• Step 3: Break the problem down into smaller, manageable parts to avoid confusion.
• Step 4: Solve each part step by step, checking each calculation for accuracy.
• Step 5: Re-read the problem to ensure the solution makes sense in the context of the question.

Example Problems and Solutions

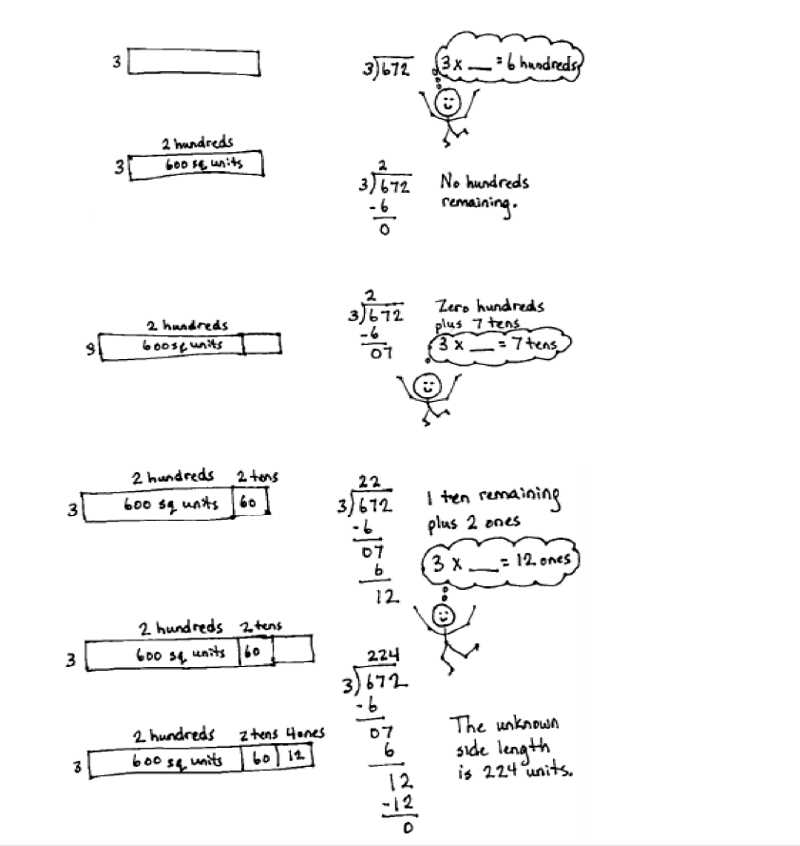
To better understand how the process works, consider the following example:

1. Problem: If there are 24 apples and they need to be divided into 4 equal groups, how many apples will be in each group?
2. Step 1: Read the problem: We are asked to divide apples into equal groups.
3. Step 2: Identify the operation: Division is required.
4. Step 3: Break the problem down: 24 apples divided by 4 groups.
5. Step 4: Perform the division: 24 ÷ 4 = 6 apples per group.
6. Step 5: Verify the solution: If we group 6 apples four times, we get 24 apples, confirming the answer is correct.

Following these steps helps ensure that each problem is tackled efficiently, making it easier to check and understand the solution.

Common Mistakes and How to Avoid Them

When working through mathematical problems, students often make certain errors that can affect their understanding and the accuracy of their solutions. These mistakes are usually a result of misunderstandings, miscalculations, or overlooking important details in the problem. Recognizing and correcting these common errors is key to improving problem-solving skills and building confidence in handling more complex tasks.

Here are some frequent mistakes and tips on how to avoid them:

• Misreading the Problem: Many students make the mistake of rushing through the problem without fully understanding what is being asked. Always take time to read the question carefully and underline key information.
• Incorrectly Applying Operations: Mixing up operations, such as using addition instead of subtraction, can lead to incorrect answers. Be sure to identify the correct operation based on the wording of the problem and the numbers involved.
• Skipping Steps: Trying to solve a problem too quickly can lead to skipping important steps in the calculation process. Make it a habit to solve problems step-by-step, writing each part of the process down for clarity.
• Forgetting to Check Work: Many errors can be avoided by simply double-checking the work. After solving a problem, take a moment to review each step and ensure the solution makes sense.
• Overlooking Place Value: Confusion with place value is a common issue, especially when working with larger numbers. Pay attention to the position of each digit and ensure the correct value is assigned to each part of the number.

By being aware of these common mistakes and actively working to avoid them, students can improve their accuracy and confidence in solving problems.

Strategies for Mastering Module 4 Topics

Mastering the concepts in this section requires both understanding the theory behind the topics and developing practical skills through consistent practice. By using effective strategies, students can deepen their comprehension, improve problem-solving abilities, and feel more confident in applying these concepts in various scenarios. The following strategies will guide learners through the process of mastering these essential skills.

Key Approaches for Success

To achieve mastery, students can use a variety of approaches that reinforce learning and improve retention:

• Practice Regularly: Consistent practice is essential. The more problems students solve, the better they understand how to apply the concepts in different contexts.
• Use Visual Aids: Diagrams, charts, and number lines can help visualize operations and reinforce understanding of relationships between numbers.
• Break Down Problems: Breaking down complex problems into smaller, manageable steps can help students avoid feeling overwhelmed and ensure they follow a clear, logical process.
• Work with Others: Collaborating with peers allows students to discuss strategies, explain concepts, and learn from different perspectives, which can enhance understanding.
• Review Mistakes: Reviewing errors is an important part of the learning process. Analyzing mistakes helps identify where misunderstandings occurred and provides an opportunity to correct them.

Additional Tips for Mastery

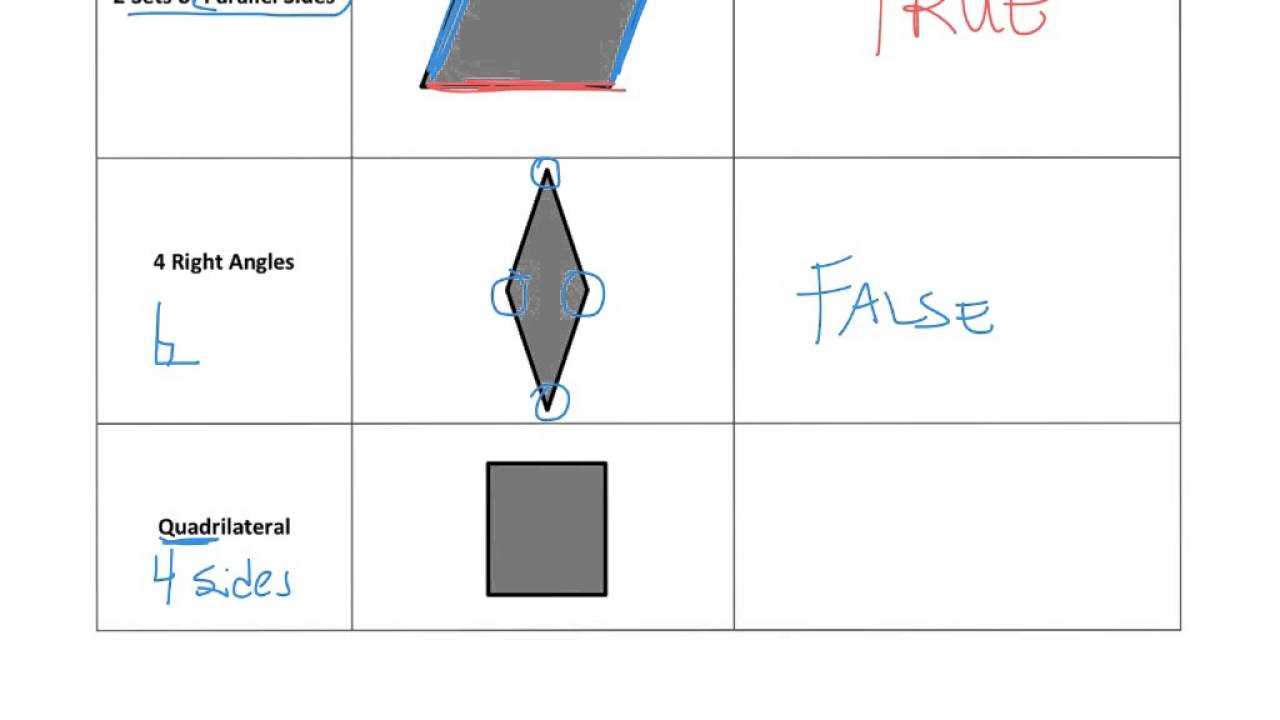
In addition to the core strategies, the following tips can help students further improve their skills:

1. Stay Organized: Keep notes and solutions organized for easy reference. This helps track progress and provides a clear overview of key concepts.
2. Apply Real-World Examples: Relate the concepts to real-life situations, such as shopping or sharing items, to make learning more relevant and engaging.
3. Ask for Help: If certain topics are difficult to understand, asking for clarification from a teacher or tutor can provide additional support and guidance.

By applying these strategies, students will be well-equipped to master the concepts in this section and build a strong foundation for more advanced topics in the future.

How to Use the Answer Key Effectively

An answer guide can be an invaluable tool for checking your work, but it’s important to use it in a way that enhances your learning rather than simply providing quick fixes. The key to using a solution guide effectively lies in understanding the reasoning behind the answers and applying that knowledge to similar problems. By approaching the guide thoughtfully, students can strengthen their problem-solving abilities and improve their overall comprehension.

Step-by-Step Approach for Maximizing the Guide

Instead of immediately referring to the provided solutions, follow this method to gain the most benefit:

• Attempt the Problem First: Always try solving the problem on your own before looking at the solution. This helps identify areas where you need improvement and builds critical thinking skills.
• Use the Solution to Check Your Work: After solving a problem, check the guide to see if your answer matches. If it doesn’t, review each step and compare your process with the solution to identify any mistakes.
• Understand the Reasoning: Don’t just memorize the answer. Focus on understanding the logic behind each step in the solution. This will help you apply the same approach to similar problems in the future.
• Ask Questions: If you don’t understand why a particular method was used or why the answer is what it is, seek clarification. Understanding the method behind the solution is crucial to mastering the topic.

Common Pitfalls to Avoid

While using a solution guide is helpful, there are a few common mistakes to be aware of:

• Relying Too Much on the Guide: Using the guide too frequently can prevent you from fully developing problem-solving skills. It’s important to rely on it only as a tool for verification, not as a crutch.
• Skipping Steps: Simply looking at the final answer without reviewing the steps can prevent you from understanding the process. Always review the entire solution.
• Not Reflecting on Mistakes: If the answer doesn’t match, take the time to analyze what went wrong. Understanding why a mistake happened is just as important as finding the right solution.

By using the solution guide as a learning tool rather than just a reference, you can reinforce key concepts, enhance your problem-solving skills, and ensure that your understanding of the material is solid.

Support Materials for Grade 3 Learning

In any educational journey, having access to additional resources can greatly enhance understanding and provide the support needed to succeed. When working through the concepts in this course, various supplementary materials are available to reinforce key topics, clarify difficult areas, and offer further practice. These tools serve as a valuable asset for both students and educators, ensuring a comprehensive grasp of the material.

Types of Support Materials

To facilitate learning, several types of resources are commonly used:

• Workbooks and Practice Sheets: These offer students extra problems to solve, reinforcing the lessons learned in class. They help solidify understanding and provide an opportunity to practice at their own pace.
• Interactive Learning Tools: Websites and apps can provide interactive exercises, making learning engaging and allowing students to get instant feedback on their progress.
• Teacher Guides and Lesson Plans: Educators can benefit from detailed lesson plans and guides that offer structured approaches to teaching each topic, including tips on how to explain complex concepts in simple terms.
• Online Video Lessons: Video tutorials can visually explain concepts, offering students the chance to see problem-solving methods step by step, often with visual aids like diagrams or animations.

How to Utilize These Resources Effectively

To make the most of these support materials, it’s essential to use them in conjunction with regular study routines:

• Supplement Regular Learning: Use workbooks and interactive tools alongside regular lessons to reinforce understanding and give students extra practice opportunities.
• Review Difficult Topics: If a particular concept is challenging, turn to video lessons or teacher guides to gain a deeper understanding. These resources often provide additional examples or alternative explanations.
• Track Progress: Many online platforms allow students to track their progress over time, providing valuable insights into areas that need further attention.
• Collaborate with Peers: Study groups and online discussion forums can provide peer-to-peer support, where students can share tips, solve problems together, and help each other overcome challenges.

Using these supplementary materials effectively can make a significant difference in a student’s ability to grasp new concepts and perform well in their coursework. These resources not only support learning but also foster a deeper understanding and greater confidence in applying the skills gained.

Practice Problems for Module 4

Practicing problems is an essential part of mastering any topic. By working through various exercises, students can reinforce their understanding, identify weak areas, and become more confident in their ability to solve similar problems independently. In this section, we will explore a range of problems that target the key concepts covered in this unit, providing both challenge and support for learners at different levels.

These practice exercises are designed to help solidify the foundational skills needed for success in the unit. They range from straightforward problems that test basic comprehension to more complex tasks that require deeper problem-solving strategies. The goal is to provide a variety of scenarios that encourage critical thinking and promote active learning.

Example Problems

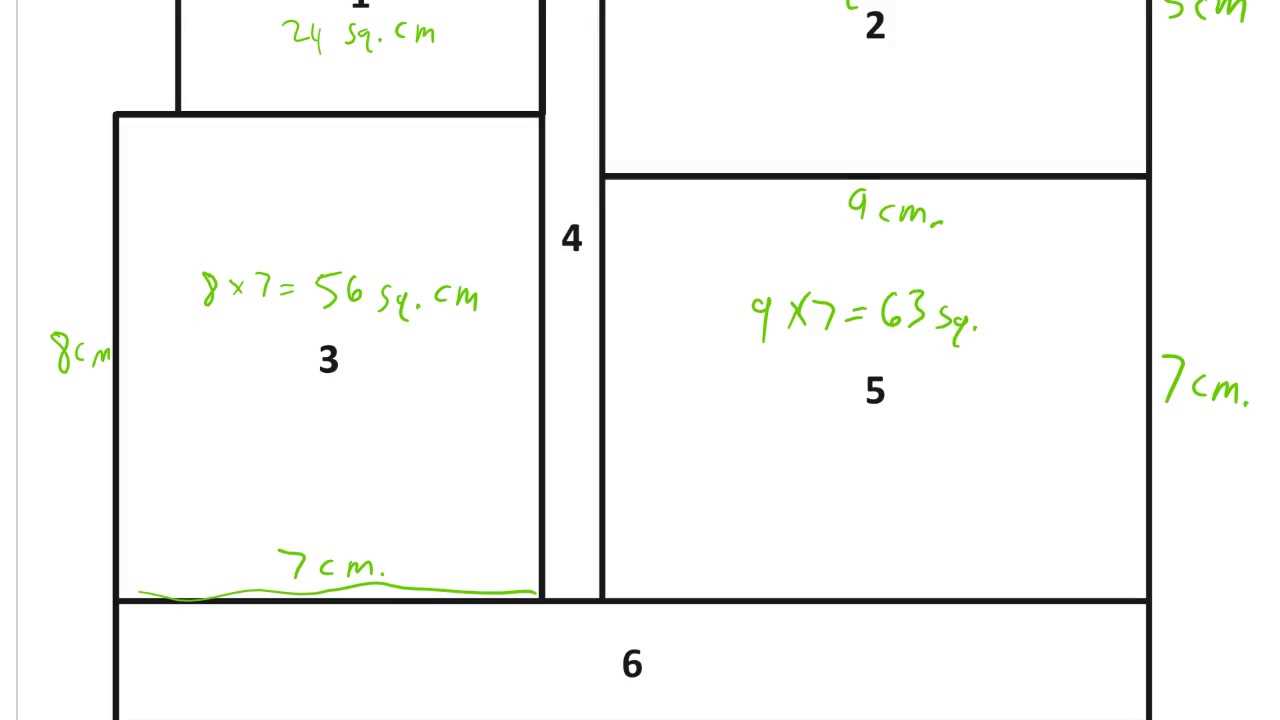
Below are some example problems for practice:

• Problem 1: Solve the following addition problem: 356 + 249 = ?
• Problem 2: Subtract: 572 – 198 = ?
• Problem 3: Multiply: 23 × 6 = ?
• Problem 4: Divide: 144 ÷ 12 = ?
• Problem 5: Word problem: If you have 5 boxes, each containing 24 items, how many items are there in total?

Tips for Solving Problems

To make the most of these exercises, keep these tips in mind:

• Read Carefully: Make sure to fully understand each problem before starting to solve it. This can help prevent unnecessary mistakes.
• Work Step-by-Step: Break down each problem into manageable steps. This will help you stay organized and ensure accuracy.
• Check Your Work: After solving a problem, always go back and verify your answer. Checking your calculations can prevent simple errors.
• Seek Help When Needed: If you’re struggling with a particular problem, don’t hesitate to ask for help. Practice makes perfect, but sometimes extra guidance is necessary to move forward.

By consistently practicing these problems, students can build a strong foundation of skills and be well-prepared for more complex challenges in the future. Remember, the more you practice, the more confident and proficient you will become.

Exploring Word Problems in Module 4

Word problems are an excellent way to apply mathematical concepts to real-life situations. They encourage critical thinking, help develop problem-solving skills, and allow students to connect abstract ideas with tangible scenarios. In this section, we will explore several word problems that reinforce the key concepts of this unit. These problems are designed to challenge students while providing opportunities to practice different strategies for finding solutions.

Types of Word Problems

Word problems often come in various forms, each requiring different approaches to solve. Below are some common types found in this section:

Problem Type	Description
Addition and Subtraction	These problems involve adding or subtracting numbers to find the total, difference, or part of a whole.
Multiplication and Division	In these problems, students must use multiplication or division to solve for a missing number in a given scenario.
Mixed Operations	These problems require a combination of addition, subtraction, multiplication, and division to find the correct solution.

Example Word Problems

Here are some example word problems for practice:

• Problem 1: If Sarah has 12 apples and she gives 3 to her friend, how many apples does she have left?
• Problem 2: A box contains 6 rows of 5 pencils. How many pencils are in the box?
• Problem 3: A baker baked 48 muffins. If each box can hold 6 muffins, how many boxes will the baker need?
• Problem 4: Jenny bought 3 packs of stickers. Each pack contains 8 stickers. How many stickers did Jenny buy in total?

By practicing word problems like these, students can develop a stronger understanding of how mathematical concepts work in real-world contexts. These exercises encourage logical reasoning and help improve overall problem-solving abilities.

Reviewing the Answer Key Solutions

Reviewing solutions to problems is a vital part of the learning process. It allows students to understand the reasoning behind each step, identify any mistakes, and gain clarity on how to approach similar challenges in the future. This section focuses on walking through the solutions, providing detailed explanations, and offering insights into common strategies used to reach the correct outcomes.

By analyzing the solutions thoroughly, students can better grasp the techniques and approaches necessary to solve problems independently. It’s important not only to check if the final answer is correct, but also to understand the method used to arrive at it. This deeper understanding will reinforce learning and help students avoid repeating the same mistakes in future exercises.

Step-by-Step Breakdown

For each problem, the solution will be broken down into smaller, manageable steps. This will help clarify the thought process behind each calculation and ensure a clear understanding of the methodology. Here is a general approach to reviewing solutions:

• Check the operations: Ensure the correct mathematical operation (addition, subtraction, multiplication, division) was applied.
• Verify calculations: Double-check the computations to confirm they were performed correctly.
• Examine units and context: Ensure that the solution makes sense in the context of the problem, especially when dealing with word problems.
• Compare with expected outcome: Compare the solution to the expected result, and ensure it aligns with the problem’s context.

By following these steps, students can develop a stronger sense of accuracy and become more confident in their problem-solving abilities. The more often you review and understand the solutions, the more effective your learning will be.

Understanding Module 4 Assessment Criteria

To effectively evaluate progress in the learning process, it’s essential to understand the criteria used for assessment. These criteria help measure a student’s ability to apply various concepts and techniques learned throughout the lessons. Knowing what is expected allows students to focus on the right areas and prepares them for achieving success in their evaluations.

Assessment typically involves examining both the accuracy of the results and the reasoning behind the methods used. Whether solving simple or complex problems, students must demonstrate a clear understanding of the operations, logic, and procedures required to reach a solution. This section will explore the key elements that teachers focus on when assessing student performance.

Key Assessment Focus Areas

Criteria	Description
Conceptual Understanding	How well the student grasps the key principles and applies them in different situations.
Accuracy of Solutions	Correctness of the answers produced, including both calculations and final results.
Problem-Solving Skills	Ability to approach and solve problems logically, considering all relevant steps and methods.
Application of Procedures	How well the student can use specific techniques to solve various types of problems.
Communication of Reasoning	Clarity in explaining the thought process and reasoning behind each solution.

Each of these criteria plays a crucial role in determining whether a student has mastered the material and can effectively apply it in real-world contexts. Understanding the focus of assessments helps students prepare better, ensuring they can showcase both their knowledge and their ability to think critically and solve problems efficiently.

How Module 4 Prepares for Future Learning

Building a strong foundation in the early stages of education is crucial for tackling more advanced topics in the future. The lessons and concepts covered in this section help develop essential skills that will be useful as students move on to more complex subjects. By mastering the principles taught here, students are equipped with tools they can apply to a variety of disciplines and real-life situations.

Each lesson is designed to not only reinforce basic concepts but also to encourage deeper critical thinking. This prepares students for future learning by fostering analytical skills and problem-solving techniques that are essential for success in advanced studies.

Skills Developed for Future Learning

• Problem-Solving Strategies: Students learn to break down complex problems into manageable steps, a skill crucial for tackling higher-level challenges.
• Logical Thinking: The lessons promote clear and structured thinking, enabling students to approach unfamiliar situations with confidence and precision.
• Critical Reasoning: Students practice analyzing information critically, which is important for understanding and solving problems in more advanced topics.
• Conceptual Connections: The ability to link new ideas to existing knowledge is emphasized, allowing for a more integrated understanding of future material.

Preparing for Advanced Concepts

The foundation set in this section serves as a stepping stone for tackling more intricate concepts in the coming years. By mastering the essential skills and techniques now, students are better prepared to handle the increasing complexity of future topics, ensuring a smoother and more successful educational journey.

How Parents Can Assist with Homework

Parental involvement plays a crucial role in a child’s academic success. When it comes to homework, parents can offer support in a way that enhances their child’s learning experience without doing the work for them. By providing the right kind of help, parents can foster independence, boost confidence, and encourage a positive attitude toward learning.

Helping with homework doesn’t mean giving answers or solving problems directly. Instead, it’s about guiding children through the process and creating a supportive environment where they feel comfortable tackling challenges on their own. With the right approach, parents can equip their children with valuable skills that will benefit them throughout their education.

Practical Tips for Parents

• Create a Consistent Study Routine: Set aside a regular time and quiet space for homework, helping your child stay focused and organized.
• Encourage Problem-Solving: Rather than providing solutions, ask guiding questions that encourage your child to think critically and work through problems independently.
• Break Down Complex Tasks: If the homework is overwhelming, help your child break it into smaller, more manageable steps to avoid frustration.
• Provide Positive Reinforcement: Celebrate small victories along the way, reinforcing effort and persistence, which can motivate your child to keep working hard.

Creating an Effective Homework Environment

Aside from offering guidance, it’s essential to establish an environment that supports focus and concentration. Make sure your child has all the materials they need, eliminate distractions, and encourage breaks when needed. A well-structured environment helps students stay on track and be more productive while completing assignments.

Benefits of Completing Module 4 Exercises

Engaging with the exercises provided in this educational unit offers numerous advantages for students, not only enhancing their knowledge but also developing key skills that will support future learning. By actively participating in the exercises, learners deepen their understanding of fundamental concepts and improve their ability to apply them to real-world situations. The repetitive nature of the tasks encourages mastery and boosts overall confidence in problem-solving abilities.

These exercises are designed to challenge students and push their cognitive limits, promoting critical thinking and perseverance. Additionally, completing the tasks helps students build a strong foundation for more advanced topics they will encounter later in their academic journey. The benefits of consistent practice are vast, ranging from skill development to increased academic motivation.

Key Advantages

• Enhanced Understanding: Regular practice strengthens comprehension, ensuring that students grasp essential concepts more effectively.
• Improved Problem-Solving: The exercises encourage students to think critically and develop strategies for solving complex problems independently.
• Increased Confidence: Successfully completing tasks fosters a sense of accomplishment, boosting self-confidence in students’ abilities to tackle new challenges.
• Better Retention: Repetition helps to solidify the knowledge learned, making it easier for students to retain and recall key information when needed.

Building Skills for the Future

By focusing on consistent practice and applying learned concepts to new situations, students can significantly enhance their preparedness for future academic challenges. The skills developed through these exercises are not just useful for current coursework, but also essential for continued growth and success in later learning stages. Completing these tasks lays the groundwork for more advanced subjects and helps students build lifelong learning habits.

Next Steps After Completing Module 4

After finishing the tasks in this unit, students are encouraged to continue building on the knowledge they’ve gained and take the next steps to reinforce and expand their understanding. This process involves applying newly acquired skills to more complex problems, revisiting key concepts for deeper comprehension, and preparing for the challenges ahead. It is essential to approach the subsequent stages with a mindset of growth and curiosity, ensuring that the foundation laid in this unit supports future learning experiences.

The next steps focus on further strengthening the concepts learned, broadening the scope of the material, and exploring real-world applications. By engaging with new challenges and reviewing the work done, students can solidify their grasp on the subject and improve their ability to approach diverse topics with confidence.

Consolidating Knowledge

• Review Key Concepts: Go back to areas that were challenging and review them to ensure full comprehension. Use additional resources or seek help if necessary.
• Practice Application: Solve new problems that build on the skills developed in this unit, applying them to different contexts to deepen understanding.
• Collaborative Learning: Engage with peers to discuss different approaches to problem-solving and share strategies. Collaborative discussions can reveal new perspectives.

Preparing for Future Learning

• Explore New Topics: Start exploring upcoming subjects that are connected to the current material. Understanding how the concepts fit into the larger curriculum helps make connections.
• Set Personal Goals: Set clear, achievable learning goals to ensure that future work is focused and targeted. This will help maintain momentum and progress.
• Seek Additional Resources: Look for supplementary materials such as online tutorials, books, or videos that reinforce the concepts covered in the current unit.

By following these next steps, students can enhance their learning experience, ensuring that the knowledge gained in this unit becomes an integral part of their educational journey. The key is to stay engaged, remain curious, and continue pushing the boundaries of what they can achieve.