
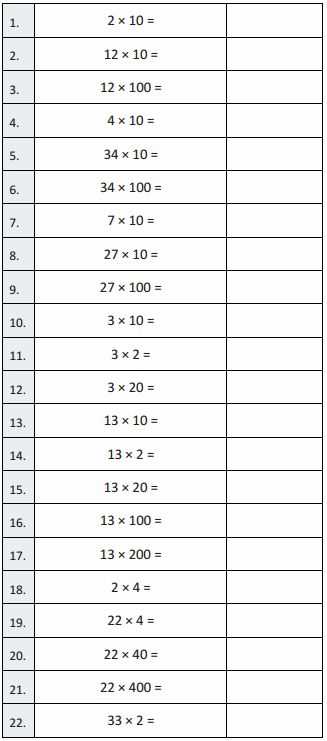
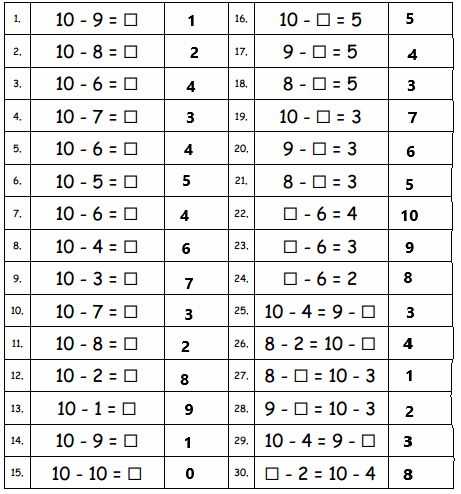
In this section, we will explore the essential topics and methods that are central to solving complex problems typically found in elementary-level math curricula. The focus is on helping students develop a deeper understanding of mathematical operations and strategies, fostering problem-solving abilities that are applicable in various contexts.
Clear explanations and practical examples will guide learners through each step, providing them with the tools to tackle similar challenges independently. By breaking down the content into manageable pieces, students can enhance their comprehension and confidence in the subject.
Through this process, it becomes easier to grasp new concepts and improve performance on future assignments. This guide is designed to assist both students and educators in navigating the material with clarity and effectiveness.
Complete Guide to Elementary-Level Mathematics
This section serves as a comprehensive resource for mastering core concepts in the early stages of advanced numerical learning. It emphasizes developing a strong foundation through structured problem-solving techniques, which are critical for overcoming challenges encountered in various mathematical topics. Students will gain the necessary skills to tackle increasingly complex tasks with confidence and clarity.
Building a Strong Foundation
At this level, students are introduced to more intricate concepts that require logical reasoning and attention to detail. By breaking down problems into simpler steps and focusing on fundamental principles, learners can better understand how to approach and solve various types of exercises. This method not only supports their current studies but also prepares them for future mathematical endeavors.
Improving Problem-Solving Skills
Fostering problem-solving abilities is at the heart of this approach. By guiding students through step-by-step solutions and offering clear explanations, they are equipped to solve even the most challenging problems on their own. This section provides both strategies and practice problems, ensuring that learners develop the skills needed to excel in future tasks and assessments.
Understanding Module 2 Lesson 15
This section focuses on mastering essential concepts that help students approach more advanced numerical operations with ease. By exploring various techniques and strategies, learners can deepen their understanding of the material and apply their knowledge to real-world problems. The content is designed to enhance logical thinking and foster a solid grasp of core principles that are vital for academic success.
Through detailed explanations and practical examples, students will be able to break down complex problems and recognize patterns that make solving them more straightforward. This part of the curriculum aims to strengthen critical thinking and reinforce the ability to tackle challenging exercises with confidence.
Key Concepts in Lesson 15 Answer Key
This section highlights the fundamental principles covered in this part of the curriculum, designed to help students grasp essential techniques and strategies. Understanding these concepts is crucial for progressing through the material and solving related problems with confidence. Each concept is broken down into smaller, manageable steps to ensure clarity and better comprehension.
Core Principles
- Understanding numerical relationships and patterns
- Applying arithmetic operations to real-world situations
- Developing problem-solving strategies for multi-step exercises
Step-by-Step Problem Solving
Breaking down problems into smaller steps helps students navigate complex tasks. By focusing on one aspect at a time, learners can improve their ability to solve similar problems independently. Here are some steps that make the process more effective:
- Identify the key information in the problem
- Determine which operations are required
- Execute each step carefully and check the result
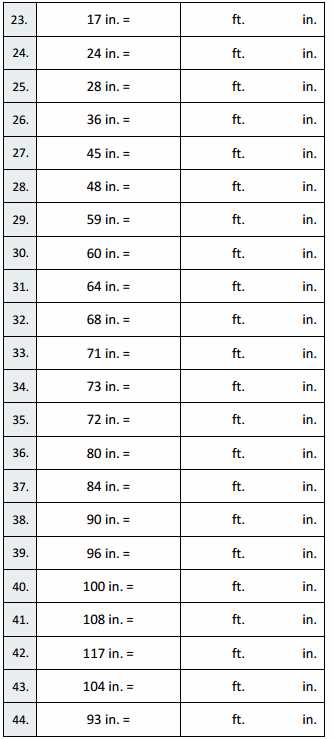
Step-by-Step Solution for Students
This section provides a clear and structured approach to solving complex problems, breaking them down into simple, manageable steps. Each problem-solving strategy is explained in detail, ensuring that students can follow along and apply the same method to similar tasks. The goal is to build confidence by guiding learners through the process, helping them understand the logic behind each step.
Breaking Down the Problem
To tackle any challenging task, it’s essential to first identify the key elements and determine the most effective strategy. Here’s how to approach each problem methodically:
| Step | Action | Explanation |
|---|---|---|
| 1 | Read the problem carefully | Understand the context and identify important information |
| 2 | Break it into smaller parts | Divide the task into manageable sections to simplify the process |
| 3 | Apply the correct operations | Use the appropriate mathematical operations to solve each section |
| 4 | Check your work | Review each step to ensure accuracy and consistency |
Practicing with Examples
Students should practice with examples similar to the ones in the guide to reinforce their understanding. By applying these steps to a variety of problems, they can master the process and become more proficient in handling complex challenges.
How to Approach Math Problems
Approaching complex numerical tasks requires a strategic mindset and a clear understanding of the underlying principles. Instead of feeling overwhelmed by the challenge, it’s essential to break the problem into manageable steps. This process helps to identify the key elements and determine the best method for finding the solution. With the right approach, even the most difficult problems become more approachable and solvable.
One effective strategy is to start by carefully reading the problem to identify what is being asked. Once the problem is understood, students can organize the information and decide which operations or formulas will lead to the correct answer. A systematic approach ensures that each step is completed accurately and logically.
Another key element is practicing consistently. The more problems students tackle, the more confident they become in using the strategies and techniques they’ve learned. This consistent practice helps build problem-solving skills and strengthens mathematical reasoning.
How to Approach Math Problems
Approaching complex numerical tasks requires a strategic mindset and a clear understanding of the underlying principles. Instead of feeling overwhelmed by the challenge, it’s essential to break the problem into manageable steps. This process helps to identify the key elements and determine the best method for finding the solution. With the right approach, even the most difficult problems become more approachable and solvable.
One effective strategy is to start by carefully reading the problem to identify what is being asked. Once the problem is understood, students can organize the information and decide which operations or formulas will lead to the correct answer. A systematic approach ensures that each step is completed accurately and logically.
Another key element is practicing consistently. The more problems students tackle, the more confident they become in using the strategies and techniques they’ve learned. This consistent practice helps build problem-solving skills and strengthens mathematical reasoning.
Practical Tips for Solving Math Problems
Solving numerical challenges can be made easier with the right strategies. By focusing on key approaches and staying organized, students can improve their problem-solving skills and reduce the likelihood of mistakes. These tips are designed to help learners approach tasks with confidence and clarity, making even the most complex problems more manageable.
Break Problems Into Manageable Steps
A great way to tackle any problem is by breaking it down into smaller, more manageable parts. Instead of trying to solve everything at once, focus on one step at a time. This not only simplifies the task but also allows you to catch mistakes early before they become bigger issues.
Double-Check Your Work
After completing each step, always take the time to double-check your calculations and logic. It’s easy to overlook small errors, but by reviewing your work, you can ensure that each part is correct before moving on to the next. This simple habit can save a lot of time and frustration in the long run.
Lesson 15 Key Learning Objectives
In this section, we will focus on the main goals and learning targets for this stage of the curriculum. These objectives are designed to help students strengthen their understanding of key concepts, develop problem-solving strategies, and enhance their ability to apply these skills in practical situations. By the end of this lesson, students should have a clearer grasp of the essential techniques needed to solve complex numerical challenges.
| Learning Objective | Description |
|---|---|
| Understand Key Concepts | Master the foundational principles behind the problem-solving methods introduced in this stage. |
| Apply Problem-Solving Strategies | Learn how to break down complex tasks into manageable steps and apply the correct operations to find solutions. |
| Build Confidence in Techniques | Gain confidence in using these techniques to tackle more advanced problems independently. |
Strategies for Mastering Module 2
To succeed in this section of the curriculum, students need to develop a deep understanding of core concepts and strategies. Mastering these skills requires a combination of practice, careful attention to detail, and effective problem-solving techniques. By approaching the material systematically and building on each concept, students can enhance their ability to solve complex tasks and perform well in assessments.
One effective strategy is to focus on the basics first. Ensure that each foundational concept is well understood before moving on to more difficult problems. This ensures that students have a solid grasp of the material and can build confidence in their abilities. Regular practice with similar problems will reinforce these concepts and help students recognize patterns that will make solving future problems easier.
Additionally, students should learn to approach each task with a clear plan. Breaking problems into smaller, more manageable steps can prevent confusion and help maintain focus throughout the process. It’s important to review the work periodically to ensure that each step is completed correctly, reinforcing the overall learning experience.
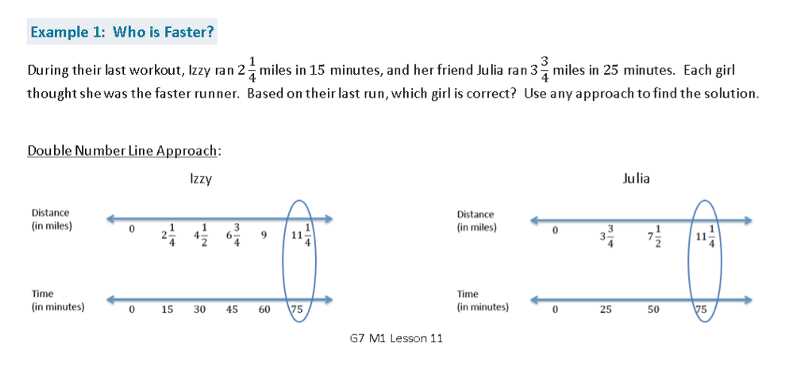
Answer Breakdown and Explanation
In this section, we will break down the solutions provided and explain the steps involved in reaching the correct answers. Understanding the process behind each solution is just as important as getting the right result. This approach helps build critical thinking skills and reinforces the concepts learned throughout the task. By carefully analyzing each step, students can gain a deeper understanding of the methods used and how to apply them in future challenges.
Step-by-Step Solution Breakdown
The first step in solving these problems is to identify the information given and determine what needs to be solved. This often involves organizing the data in a clear and logical manner. Once the information is organized, it’s important to choose the correct operations to apply. Each operation should be performed carefully, ensuring that no details are missed. After completing the necessary steps, it’s crucial to double-check the result to confirm that the calculations align with the problem’s requirements.
Common Mistakes to Avoid
While solving these problems, it’s common to make small errors, such as misinterpreting the question or applying the wrong operation. These mistakes can be easily avoided by reviewing the steps carefully and ensuring that each operation is applied correctly. Pay special attention to units of measurement, as they can sometimes cause confusion. By practicing these steps and learning from past mistakes, students can improve their accuracy and problem-solving skills.
Real-Life Applications of Math Concepts
The skills and techniques learned through problem-solving exercises are not just useful in the classroom but also have practical applications in everyday life. From budgeting and planning to measuring and organizing, these concepts play a vital role in various real-world scenarios. Understanding how to apply these skills in practical situations helps students see the value of what they’re learning and how it can be used beyond academics.
For example, understanding basic operations is essential when managing personal finances, whether it’s calculating expenses or saving for a goal. Similarly, measuring areas and volumes is important in tasks such as home renovation or cooking. Recognizing these connections between classroom learning and real-life situations enhances both engagement and comprehension.
| Application | Concepts Used | Example |
|---|---|---|
| Budgeting and Financial Planning | Addition, Subtraction, Multiplication | Tracking monthly expenses and calculating savings |
| Cooking and Baking | Fractions, Multiplication, Measurement | Adjusting recipes and measuring ingredients |
| Home Renovation | Geometry, Measurement, Division | Calculating areas of rooms for flooring or paint |
How Eureka Math Enhances Problem-Solving Skills
The approach to learning in this curriculum emphasizes developing strong problem-solving abilities. By encouraging students to understand the underlying principles of each concept, it fosters critical thinking and analytical skills. These methods help learners not only solve problems but also approach new challenges with confidence. The curriculum’s structured yet flexible approach ensures that students build the necessary skills to tackle increasingly complex tasks.
One of the key ways this approach enhances problem-solving skills is by focusing on step-by-step methods. Each problem is broken down into manageable parts, making it easier for students to comprehend and apply different strategies. This process ensures that students are well-equipped to solve problems independently, using logical reasoning and previously learned concepts.
- Critical Thinking Development: Encourages deeper understanding of problems before solving.
- Strategic Approach: Teaches students how to break down complex problems into smaller steps.
- Real-World Connections: Helps students see the relevance of problem-solving skills in everyday life.
- Confidence Building: Reinforces skills and fosters independence in solving problems.
Furthermore, this method supports continuous improvement. By regularly practicing problem-solving techniques and applying them in different contexts, students develop flexibility in their thinking. This adaptability is key when approaching unfamiliar problems or tasks in the future, ensuring long-term success in various disciplines.
Important Vocabulary for Lesson 15
Mastering key terms is essential for understanding and solving problems effectively. In any learning environment, a clear grasp of terminology helps students follow concepts more easily and apply the correct strategies. In this section, we will highlight some of the most important vocabulary terms related to the topic at hand, which are crucial for comprehending the material and excelling in problem-solving tasks.
Key Terms
Below are some essential terms that learners should familiarize themselves with to better navigate the content and its related tasks:
- Operation: A mathematical process such as addition, subtraction, multiplication, or division used to solve problems.
- Expression: A combination of numbers, symbols, and operations that represent a particular value or relationship.
- Equation: A mathematical statement that shows two expressions are equal, typically involving variables.
- Factor: A number or algebraic expression that divides another number evenly.
- Product: The result of multiplying two or more numbers or terms together.
Application of Terms
Understanding how these terms apply in various contexts is crucial for developing problem-solving skills. For example, recognizing the difference between an expression and an equation allows students to identify whether they are dealing with a statement of equality or a simplifiable relationship. By practicing the use of these terms in different problems, learners will gain a deeper understanding of their meaning and how to use them to solve complex tasks effectively.
Preparing for Upcoming Math Challenges
As students advance through their studies, they will encounter increasingly complex tasks that require both conceptual understanding and practical problem-solving skills. Preparing for these challenges involves not only reviewing previous material but also developing strategies that can help tackle new and unfamiliar topics. In this section, we will explore effective methods for preparing for upcoming challenges and how students can build confidence in their abilities.
Review Key Concepts
One of the most effective ways to prepare for future challenges is to solidify understanding of fundamental concepts. Revisiting earlier topics ensures that students have a strong foundation to build upon. Regular practice with previous material helps reinforce key skills and makes it easier to approach new topics. Focus on the following strategies:
- Identify weak areas: Review past problems to spot areas where additional practice may be needed.
- Practice regularly: Consistent practice helps maintain proficiency and build confidence.
- Apply concepts in real-world situations: Understanding how concepts are used in practical applications can make them more relatable and easier to grasp.
Develop Problem-Solving Strategies
Being able to apply learned concepts effectively requires good problem-solving strategies. It’s important for students to have a clear approach when tackling each new challenge. Here are some helpful strategies:
- Break down the problem: Divide complex tasks into smaller, more manageable steps.
- Look for patterns: Identifying patterns can often lead to quicker solutions.
- Check work: Always review the solution to ensure it makes sense and meets the criteria.
By reviewing concepts and applying these problem-solving strategies, students can approach upcoming challenges with greater confidence and skill, setting themselves up for success in future tasks.
Teacher’s Guide to Module 2 Lesson 15
This section provides an overview and key strategies for instructors preparing to guide students through the concepts in this particular segment of their studies. It is designed to help educators ensure that students understand the core ideas and develop the skills necessary to successfully complete the tasks. The following guidance will cover lesson preparation, teaching strategies, and tips for assessing student progress.
Lesson Preparation
Before diving into the material, it is crucial to review the objectives and the specific concepts to be taught. A clear understanding of the goals allows teachers to create a structured approach to instruction and ensure that students grasp the key ideas. Some useful steps to consider:
- Review the learning objectives: Ensure that the goals are clearly outlined for both the teacher and the students.
- Prepare materials: Organize resources such as worksheets, visual aids, and any supplementary materials that may support learning.
- Anticipate common student challenges: Be prepared to address any areas where students may struggle, such as complex problem-solving or unfamiliar terminology.
Effective Teaching Strategies
Once the preparation is complete, it’s time to focus on delivering the material in a way that is engaging and accessible to students. Here are a few strategies that can help enhance learning:
- Encourage active participation: Ask questions and involve students in discussions to maintain engagement and reinforce understanding.
- Break down complex ideas: Divide challenging tasks into smaller, manageable steps to avoid overwhelming students.
- Use real-world examples: Relate the concepts to real-life situations to help students see the relevance of what they’re learning.
- Provide instant feedback: Offer feedback during activities to address mistakes and reinforce correct understanding.
With careful preparation and a well-organized teaching approach, educators can create a productive learning environment that helps students master the material and build confidence in their abilities.
Engaging Students with Math Exercises
Keeping students actively engaged in learning can be a challenge, especially when the exercises become more complex. It’s essential to use techniques that not only capture their attention but also encourage deep thinking and problem-solving. By incorporating a variety of strategies, educators can make exercises more enjoyable and stimulating, fostering a positive learning experience.
One effective way to engage students is by incorporating interactive elements into the exercises. This can include hands-on activities, real-world examples, or even technology that allows students to visualize abstract concepts. Additionally, encouraging collaboration through group activities helps students learn from each other, fostering a sense of teamwork and improving their problem-solving skills.
Another key aspect is providing timely and constructive feedback. This helps students understand their mistakes and learn from them, which is essential for their development. Also, varying the types of problems, such as incorporating games or challenges, can make the process more dynamic and reduce the monotony often associated with traditional exercises.
Lastly, connecting the exercises to real-life scenarios helps students see the practical applications of what they are learning, making the material more relevant and engaging. By using these strategies, educators can help students stay motivated and improve their understanding of the concepts.
Improving Math Skills with Structured Exercises
Strengthening mathematical abilities requires a systematic approach that reinforces key concepts and challenges students to think critically. A structured curriculum that integrates both foundational principles and complex problem-solving exercises can significantly enhance a student’s proficiency. With a clear progression of topics and continuous practice, learners are better prepared to tackle more difficult challenges.
Effective learning tools incorporate both theoretical knowledge and practical application, offering students opportunities to apply concepts to real-world scenarios. This balanced approach helps learners grasp difficult topics more easily and boosts their confidence in problem-solving.
Key Strategies for Enhancing Problem-Solving Skills
- Consistent Practice: Regular exposure to various problem types improves fluency and enhances retention.
- Step-by-Step Solutions: Breaking down problems into manageable steps helps students grasp complex ideas more clearly.
- Interactive Learning: Using visual aids, manipulatives, and technology creates a dynamic learning environment.
- Real-Life Connections: Relating exercises to everyday situations helps students see the value of their learning.
Tracking Progress and Providing Feedback
Assessing student progress through ongoing evaluation helps identify areas of difficulty, allowing for targeted interventions. Timely and constructive feedback is essential for fostering growth, enabling students to understand their mistakes and learn from them. This personalized approach not only supports learning but also encourages self-reflection and independence in solving problems.