Go Math Chapter 4 Answer Key

In this section, we will explore the solutions to various problems and exercises presented in the fourth unit of the learning material. The focus will be on helping students understand the key concepts and develop problem-solving strategies for more effective learning.

Step-by-step explanations will guide you through the most challenging questions, highlighting methods to approach different types of tasks. By breaking down each problem, learners can strengthen their skills and gain confidence in tackling similar exercises.

The provided solutions are designed to clarify any doubts and assist in mastering the subject. Whether you’re preparing for a test or simply reviewing the material, these explanations will make the learning process easier and more efficient.

Go Math Chapter 4 Answer Key

This section provides detailed solutions and explanations for the exercises in the fourth unit. The goal is to guide learners through problem-solving processes, helping them fully grasp the concepts and methodologies needed to succeed in their studies.

Understanding the Concepts

In this unit, students will encounter a variety of tasks designed to strengthen their abilities. It’s important to focus on both the process and the final solution. By following clear and logical steps, students can confidently address even the most challenging problems.

Step-by-Step Solutions

The following solutions break down each problem into manageable steps. By studying these explanations, learners will better understand how to approach similar tasks in the future.

• Step 1: Carefully read the problem to identify key information.
• Step 2: Apply the relevant formulas or techniques to solve the problem.
• Step 3: Double-check the solution to ensure accuracy.

These methods will help develop strong problem-solving habits and make tackling new challenges easier. Whether reviewing or preparing for assessments, these solutions are an essential tool for mastering the material.

Understanding Key Concepts of Chapter 4

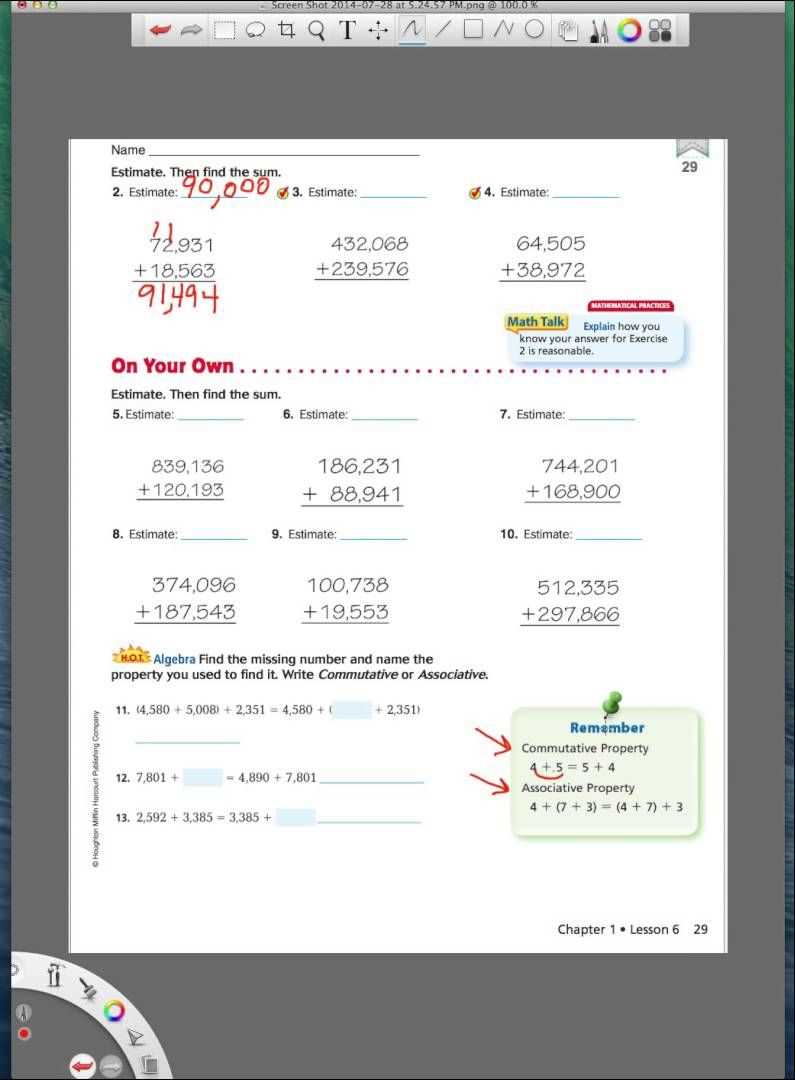
This section explores the essential ideas and principles presented in the fourth unit, focusing on providing a solid understanding of the topics covered. Mastery of these fundamental concepts is crucial for successfully solving related problems and applying the knowledge effectively in various situations.

Core Principles to Focus On

Several core principles are vital for tackling the tasks in this unit. Recognizing the relationship between these concepts will help build a strong foundation for future learning.

• Concept 1: Understanding basic operations and their application.
• Concept 2: The role of patterns in solving problems efficiently.
• Concept 3: How to break down complex tasks into simpler steps.

Applying These Concepts in Practice

Once these ideas are understood, applying them in practice becomes much easier. Here’s how to effectively use them when solving exercises:

1. Analyze the problem carefully to identify which concept applies.
2. Use appropriate strategies and steps to find the solution.
3. Check the results to ensure they align with the expected outcome.

With these key concepts in mind, learners can approach each task with confidence and a clearer understanding of the material.

How to Approach Go Math Problems

Approaching problems effectively requires a strategic mindset. In this section, we will explore techniques to help you break down tasks, understand the steps involved, and apply logical methods to find the solution. A structured approach to problem-solving will not only make tasks more manageable but also improve your understanding of the material.

Steps to Solve Complex Problems

By following a series of organized steps, learners can address each problem more efficiently. These steps can be applied to a wide range of questions and provide a consistent method for tackling new challenges.

• Step 1: Read the problem carefully and highlight key information.
• Step 2: Identify the method or formula that fits the situation.
• Step 3: Break the problem into smaller, easier-to-manage steps.
• Step 4: Perform the necessary calculations or logical steps.
• Step 5: Double-check your work and ensure the solution makes sense.

Tips for Effective Problem-Solving

In addition to following the steps above, these tips can help further streamline the process:

• Stay organized: Keep track of your work and calculations.
• Look for patterns: Identifying recurring patterns can simplify complex problems.
• Don’t rush: Take your time to think through each step carefully.

By practicing these techniques regularly, you will become more efficient and confident in solving a variety of tasks.

Step-by-Step Solutions for Chapter 4

This section provides a detailed, methodical approach to solving the exercises presented in the fourth unit. By breaking down each problem into smaller, more manageable steps, learners can develop a deeper understanding of the processes involved and improve their problem-solving skills.

Breaking Down Each Problem

Each solution follows a clear progression that starts with understanding the problem and ends with verifying the results. This structured approach ensures that learners grasp the logic behind each solution and gain confidence in their ability to tackle similar tasks in the future.

• Step 1: Carefully read the problem to identify the essential information.
• Step 2: Choose the appropriate method or strategy based on the problem type.
• Step 3: Execute the necessary calculations or logical steps to find the solution.
• Step 4: Review your results to ensure they align with the expected outcome.

Applying the Method to Practice

Once the process is understood, learners can apply it to new challenges. With regular practice, these solutions will help develop a strong foundation for solving problems more independently and efficiently.

• Tip 1: Take time to check each step for accuracy.
• Tip 2: Use visual aids like diagrams or tables if necessary.
• Tip 3: Don’t hesitate to revisit earlier steps for clarification if needed.

By following this step-by-step approach, students will gain the skills required to solve a variety of problems and excel in their studies.

Common Mistakes in Chapter 4 Exercises

As students work through the problems in this unit, certain errors tend to arise frequently. These mistakes, though common, can be easily avoided with careful attention to detail and a clear understanding of the concepts involved. Recognizing these pitfalls is an essential step in mastering the material.

Many learners struggle with misinterpreting the problem, rushing through calculations, or neglecting to check their work. Identifying these frequent mistakes helps students improve their problem-solving skills and avoid unnecessary confusion in the future.

• Misunderstanding key information: Failing to identify important details or misinterpreting the problem’s question.
• Skipping steps: Jumping ahead in the process without verifying earlier calculations.
• Rushing through solutions: Trying to finish quickly can lead to careless errors and missed opportunities for deeper understanding.
• Overcomplicating the process: Sometimes, students use unnecessary methods or try to solve problems in a more complex way than required.
• Not reviewing work: Failing to double-check results, which can lead to simple yet avoidable mistakes.

By being aware of these common mistakes, learners can focus on developing more effective strategies and refine their approach to solving problems with confidence.

Mastering Word Problems in Go Math

Word problems can often seem challenging, but with the right approach, they become much easier to solve. This section is dedicated to helping students develop strategies for interpreting and solving word problems effectively. By breaking down the text and identifying key information, students can tackle these exercises with confidence.

Breaking Down the Problem

The first step in solving any word problem is to thoroughly read and understand the question. Identify the key elements and information that will guide you to the solution. Here are some tips to help you break down the problem:

• Identify the question: What exactly is being asked? Look for key phrases like “how many,” “what is,” or “find the total.”
• Highlight important numbers: Underline or note the figures that will help in calculations.
• Understand the relationships: Pay attention to how the numbers and information are connected.

Steps to Solve Word Problems

Once you have a clear understanding of the problem, follow these steps to solve it systematically:

1. Step 1: Read the problem carefully and underline or highlight key information.
2. Step 2: Translate the words into mathematical expressions or operations.
3. Step 3: Perform the necessary calculations, one step at a time.
4. Step 4: Review your solution to ensure it makes sense in the context of the problem.

By practicing these strategies, learners can improve their ability to solve word problems and approach each task with a clear, logical mindset.

Tips for Solving Difficult Go Math Problems

When faced with challenging exercises, it’s important to approach them with a clear strategy. These types of problems can be intimidating at first, but with the right mindset and techniques, they can become manageable. The following tips are designed to help students break down complex problems, stay focused, and find the correct solutions with confidence.

• Take Your Time: Avoid rushing through the problem. Carefully read through the instructions and make sure you understand what is being asked before proceeding.
• Break the Problem into Smaller Parts: Divide the task into smaller, more manageable steps. This will make it easier to focus on one part at a time and reduce feelings of overwhelm.
• Look for Patterns: Many difficult problems have underlying patterns that can simplify the process. Identifying these patterns can save time and lead to quicker solutions.
• Revisit the Basics: If you’re stuck, review basic concepts that might be needed to solve the problem. Often, returning to fundamental principles helps clarify the approach.
• Check Your Work: After solving the problem, always take a moment to double-check your calculations and reasoning. Ensuring accuracy can prevent simple mistakes from affecting the final answer.

By following these strategies, students can build confidence in their problem-solving skills and approach difficult exercises with a structured and effective method.

Interactive Activities for Better Learning

Engaging with material through hands-on activities can significantly enhance understanding and retention. In this section, we explore different interactive exercises that allow students to apply what they’ve learned in a practical, enjoyable way. These activities not only reinforce key concepts but also make learning more dynamic and memorable.

By participating in interactive exercises, students can solidify their grasp of various concepts, practice problem-solving in real-time, and develop critical thinking skills. Whether through online tools, group tasks, or individual challenges, these activities offer an opportunity to learn actively rather than passively absorbing information.

• Interactive Quizzes: Create quizzes based on recent lessons. These can help test knowledge in a fun, competitive way.
• Collaborative Group Challenges: Working in teams allows students to discuss strategies and share problem-solving techniques.
• Visual Aids and Games: Using diagrams, charts, and online games makes abstract concepts easier to visualize and understand.
• Real-Life Scenarios: Apply concepts to everyday situations to demonstrate how they are relevant in the real world.

Incorporating these interactive methods into study routines can provide a deeper, more practical understanding of the material and make learning more engaging and effective.

Understanding Fractions in Chapter 4

Fractions can often be a challenging concept, but with the right approach, they become much easier to understand. This section focuses on the fundamentals of fractions, how they are represented, and how to manipulate them in various exercises. By mastering these concepts, students will gain a stronger foundation for working with fractional numbers in different contexts.

What Are Fractions?

At its core, a fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts are being considered, while the denominator shows how many equal parts the whole is divided into.

• Numerator: The number of parts being taken from the whole.
• Denominator: The total number of equal parts that the whole is divided into.

How to Simplify Fractions

Simplifying fractions is an important skill in working with them. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator and divide both by this number.

• Step 1: Find the greatest common divisor of the numerator and denominator.
• Step 2: Divide both the numerator and denominator by the GCD.
• Step 3: The result is the simplified fraction.

By understanding these basic concepts and practicing the steps for simplification, students will feel more confident working with fractions in exercises and real-world scenarios.

Detailed Explanation of Chapter 4 Answers

In this section, we will go through the solutions to some of the most challenging problems, breaking down each step and explaining the reasoning behind the correct responses. Understanding how to approach and solve each problem is crucial for reinforcing key concepts and improving problem-solving skills. By following these detailed explanations, students can better understand the processes involved and avoid common mistakes in similar exercises.

Problem	Solution Steps	Final Result
Problem 1: Adding Fractions	Find a common denominator. Add the numerators. Simplify the resulting fraction.	3/4
Problem 2: Subtracting Fractions	Ensure the denominators are the same. Subtract the numerators. Simplify the resulting fraction.	1/6
Problem 3: Multiplying Fractions	Multiply the numerators. Multiply the denominators. Simplify if possible.	2/15

By following the systematic approach to solving each problem, students can develop a deeper understanding of the methods used and feel more confident in tackling similar exercises. The key is practicing each type of problem to master the process and achieve accuracy in every step.

Why Practice is Essential for Success

Repetition and consistent effort are key components to mastering any skill. In this section, we will explore why regular practice is necessary for achieving long-term success. Whether it’s for reinforcing learned concepts, building confidence, or improving problem-solving abilities, practice helps solidify knowledge and creates a deeper understanding of complex ideas.

The Role of Repetition in Learning

When students engage in repetitive exercises, they not only reinforce the material they’ve learned but also become more comfortable with applying concepts in different contexts. The more they practice, the more they begin to recognize patterns and develop strategies to solve problems more effectively.

Benefit	Explanation
Improved Retention	Regular practice strengthens memory and helps retain information over time.
Increased Confidence	Frequent practice builds self-assurance, allowing students to approach problems with less fear of failure.
Faster Problem-Solving	Through repeated practice, students become quicker at recognizing solutions and implementing effective strategies.

How Practice Leads to Mastery

As students practice consistently, they start to see improvements not only in accuracy but in efficiency. This mastery comes from understanding the underlying principles and being able to apply them without hesitation. Therefore, continued practice is vital for ensuring lasting success in any learning endeavor.

Go Math Chapter 4 Review for Students

This section provides a comprehensive overview of key concepts and skills learned in the fourth unit. It’s designed to help students consolidate their understanding and prepare for assessments by reviewing important topics, practice strategies, and common pitfalls to avoid. Reinforcing these ideas will enable students to approach future problems with confidence and clarity.

Key Topics Covered

Throughout this section, students will have encountered various mathematical concepts and operations. The main focus areas are as follows:

• Fractions: Understanding parts of a whole and operations with fractions.
• Decimals: Converting between fractions and decimals, as well as performing calculations.
• Word Problems: Applying mathematical concepts to solve real-life situations.
• Measurement: Units of measurement and their conversions.

Study Tips for Mastery

To make the most of this review, students should focus on the following strategies:

1. Practice regularly: Consistent practice is essential for retaining information and improving problem-solving speed.
2. Review mistakes: Take time to go over incorrect answers and understand where the errors occurred.
3. Ask for help: When stuck, seek clarification from teachers or peers to gain a better understanding.
4. Use visual aids: Draw diagrams or use objects to represent fractions and other concepts for better visualization.

By focusing on these strategies and revisiting key topics, students can solidify their knowledge and enhance their performance in upcoming tasks and assessments.

How to Use the Answer Key Effectively

Using a solution guide can be a helpful tool when navigating through exercises, but it’s important to approach it with a strategy that maximizes its benefits. Simply checking answers is not enough–engaging with the material thoughtfully ensures that the learning process is productive. By understanding how to utilize these resources correctly, students can strengthen their grasp of the material and enhance their problem-solving skills.

To use the solution guide effectively, follow these steps:

• Attempt the Problem First: Always try to solve the problem on your own before referring to the guide. This encourages independent thinking and helps identify areas where you need further understanding.
• Analyze the Solution: Once you check the provided solution, take time to break it down step-by-step. Understanding how the problem was approached is crucial to learning the underlying concepts.
• Learn from Mistakes: If your solution differs from the one in the guide, don’t just move on. Review where you went wrong and understand the reasoning behind the correct steps.
• Reattempt Similar Problems: After reviewing the solution, work on similar problems to reinforce the concepts. Practice helps to solidify knowledge and improve problem-solving skills.
• Ask for Clarification: If you still don’t understand a solution, seek help from a teacher or peer to clarify any confusion. Understanding the ‘why’ behind each step is essential for mastery.

By using the solution guide as a learning tool rather than just a shortcut, students can make meaningful progress in mastering the material and building confidence in their abilities.

Test Preparation with Go Math Answers

Preparing for an assessment involves more than just memorizing formulas or solutions–it’s about understanding the principles behind each concept and practicing how to apply them. Using a solution guide effectively can help reinforce this understanding by providing clarity on how to approach different types of problems. When used thoughtfully, these guides can be a crucial part of your test preparation routine, helping you identify weak spots and build confidence.

To prepare for your upcoming tests, follow these strategies:

• Review Key Concepts: Before diving into solutions, take time to revisit important topics. Focus on understanding the core principles and techniques that are likely to appear on the test.
• Practice Problems: Use the problems from your exercises as practice. Work through them without looking at the solutions immediately to test your ability to recall and apply concepts on your own.
• Check Your Work: After solving a problem, refer to the solution guide to verify your approach and answer. Take note of any differences in the method you used and the one presented in the guide.
• Understand Mistakes: Mistakes are valuable learning opportunities. When you encounter errors, carefully analyze what went wrong and how the correct solution was derived.
• Simulate Test Conditions: Create a timed environment to solve a set of problems. This helps you get used to working under pressure and improves your speed and accuracy during the test.

Using a solution guide strategically can transform it into a powerful tool for mastering concepts and excelling in assessments. By actively engaging with the material and learning from each problem, you’ll be well-prepared for success.

Improving Your Math Skills with Chapter 4

Enhancing your problem-solving abilities involves more than just learning techniques; it’s about understanding the underlying principles and being able to apply them in different contexts. By working through exercises and reviewing solutions, you can strengthen your skills and gain confidence in your ability to tackle various types of problems. Chapter 4 offers valuable opportunities to refine your skills and deepen your understanding.

To make the most of this section, consider the following strategies:

• Master Basic Concepts: Begin by ensuring you have a strong grasp of the foundational ideas. These form the building blocks for more complex problems.
• Focus on Step-by-Step Problem Solving: Break down each problem into manageable steps. This method helps you stay organized and minimizes errors.
• Practice Regularly: Repetition is key to improvement. Set aside time each day to work on problems, even if you feel confident in the material.
• Learn from Mistakes: When you make an error, take the time to understand why it happened. This is where true learning happens–by identifying gaps and correcting them.
• Challenge Yourself: Don’t shy away from more difficult problems. Pushing yourself to solve tougher questions can accelerate your growth and increase your problem-solving efficiency.

By consistently practicing and applying the strategies outlined in this section, you’ll be well on your way to mastering essential skills and becoming more proficient in solving problems. The key is persistence and an active approach to learning.

What to Do After Completing the Exercises

Once you have finished working through the exercises, the next step is to reflect on what you’ve learned and ensure that you fully understand the concepts. It’s important to review your work and evaluate how well you’ve grasped the material. The process doesn’t stop at simply completing the tasks; the true value comes from reflecting on your performance and reinforcing what you’ve learned.

Review Your Solutions

Go through each solution carefully to identify any mistakes or areas of confusion. If you found some questions difficult, take the time to break them down step by step again. Understanding why a mistake was made is a powerful way to avoid repeating it in the future.

Identify Areas for Improvement

Even if you completed most of the exercises correctly, there may still be areas where you can improve. Focus on topics or problem types that you found challenging. Practicing these areas repeatedly will help solidify your understanding and make you more confident in your abilities.

Additionally, it can be helpful to seek additional resources or ask for help from a teacher or peer if you continue to struggle with certain concepts. This extra support can offer new perspectives and techniques for mastering difficult material.

Finally, review the overall progress you’ve made. With each set of problems, you should notice an improvement in both speed and accuracy. This continuous practice and self-evaluation will contribute to long-term success and mastery of the material.