Go Math Standards Practice Book Grade 3 Answer Key

Effective learning requires more than just completing exercises; it involves understanding the reasoning behind each solution. By breaking down problems step-by-step, students can develop a deeper understanding of key concepts. This approach not only enhances problem-solving skills but also builds confidence in tackling more complex challenges.

The resources provided for this educational section are designed to assist learners in mastering fundamental principles. With detailed solutions and explanations, students can review their work and identify areas that require more focus. This method encourages self-assessment and allows learners to progress at their own pace.

By leveraging these materials, learners can strengthen their skills, clarify any confusion, and improve their overall performance in mathematics. The ability to cross-reference solutions ensures that students gain a solid grasp of essential topics while also learning strategies to overcome common obstacles.

Go Math Standards Practice Book Grade 3 Answer Key

This section provides a comprehensive guide to solving exercises found in the third-level learning materials. It includes step-by-step instructions that explain the approach to each problem, helping students navigate through their assignments with clarity. By reviewing the solutions, learners can develop a stronger grasp of important concepts and improve their problem-solving abilities.

Through detailed breakdowns, this guide highlights essential methods and techniques, ensuring that students can see the process behind each solution. With these explanations, common difficulties are addressed, making it easier for students to understand where they went wrong and how to correct their mistakes.

By regularly referencing these resources, students can reinforce their knowledge, gain confidence, and achieve mastery in essential skills. This guide serves as a valuable tool for anyone seeking to improve their understanding and performance in key areas of study.

Understanding Go Math Grade 3 Format

The structure of the third-level learning materials is designed to introduce students to essential concepts in a logical and engaging way. Each section focuses on specific skills, building on previous knowledge while gradually increasing in complexity. The format is structured to ensure that students can follow along easily, developing a solid understanding of core topics.

Key components of the layout include:

• Clear Instructions: Step-by-step guides that explain each process in detail.
• Variety of Exercises: A mix of problems that range in difficulty to challenge learners at every stage.
• Visual Aids: Diagrams and illustrations that help clarify difficult concepts and demonstrate problem-solving methods.
• Practice Questions: Opportunities for students to apply what they’ve learned and reinforce their understanding.

This structure allows students to work at their own pace while developing both their analytical and practical skills. It fosters independence and critical thinking, empowering learners to solve problems confidently and effectively.

How to Use the Answer Key Effectively

To get the most out of the solution guide, it’s important to approach it strategically. Simply looking at the final results without understanding the steps can limit learning. Instead, focus on using the guide to reinforce concepts and identify areas that require further attention.

Start by attempting the exercises on your own. Afterward, compare your approach with the solutions provided. Pay close attention to the reasoning and methods used to reach each conclusion. This will help you recognize any mistakes and understand the correct process. Additionally, try to solve similar problems on your own before checking the solutions again to ensure your understanding is solid.

Using the resource as a learning tool rather than a shortcut allows you to track progress, build confidence, and ultimately improve your skills. Consistently reviewing your work and referring to the guide will make it easier to tackle future challenges and gain a deeper comprehension of core topics.

Key Concepts in Go Math Grade 3

At the third level of learning, students are introduced to essential ideas that lay the foundation for future studies. These concepts build upon previous knowledge and deepen understanding in various areas. Mastering these topics equips learners with the skills they need to approach more complex challenges in the future.

Core Areas of Focus

• Number Operations: Understanding addition, subtraction, multiplication, and division of whole numbers and fractions.
• Place Value: Recognizing the value of digits in multi-digit numbers and understanding how to round numbers.
• Measurement: Learning about units of measurement, time, and comparing lengths, weights, and volumes.
• Geometry: Identifying shapes, understanding their properties, and calculating perimeter and area.
• Data Analysis: Collecting, interpreting, and representing data in various formats, such as bar graphs and tables.

Mathematical Thinking Development

• Problem-Solving Skills: Learning how to approach and solve real-world problems using the concepts taught.
• Logical Reasoning: Developing the ability to make connections between different mathematical ideas and applying them to new situations.
• Patterns and Relationships: Recognizing and using patterns to solve problems more efficiently.

These key ideas are not only critical for success in later education but also for applying logical thinking in everyday life. Building a strong understanding of these concepts ensures that students have a solid foundation for tackling future academic challenges.

Detailed Solutions for Math Problems

Having clear and thorough explanations for each problem is essential for mastering essential skills. By breaking down each task into manageable steps, students can understand the logic behind every solution, making it easier to apply similar techniques in future exercises. Detailed solutions not only clarify how to get the correct result but also provide insight into the thought process required for problem-solving.

Steps to Approach Problems

• Understand the Question: Begin by carefully reading the problem to determine what is being asked and identify the key information.
• Choose the Right Method: Select an appropriate strategy based on the type of problem, whether it’s calculation, comparison, or pattern recognition.
• Break It Down: Simplify the task by breaking it into smaller steps, which makes it easier to solve progressively.
• Check Your Work: Once the solution is found, review each step to ensure accuracy and make corrections if necessary.

Examples of Detailed Solutions

• Problem-Solving Approach: For a word problem, identify keywords that guide the method to use and apply logical reasoning to arrive at the solution.
• Visual Aids: Use diagrams or charts when needed to visualize the problem and help in understanding complex concepts.
• Step-by-Step Calculations: Each calculation should be explained clearly, showing every step in the process to help students understand how the result was achieved.

By following these guidelines and referring to the solutions provided, learners can strengthen their understanding and develop the skills needed to tackle similar problems with confidence and ease.

Common Mistakes to Avoid in Go Math

When working through exercises, it’s easy to make errors that can derail understanding and progress. Recognizing and avoiding these common mistakes is crucial for improving performance and building a solid foundation for more advanced concepts. By identifying frequent pitfalls, students can take proactive steps to ensure accuracy and strengthen their problem-solving skills.

Typical Errors and How to Avoid Them

Common Mistake	How to Avoid It
Misunderstanding the Question	Read the problem carefully, highlight key information, and ensure you understand what is being asked before proceeding.
Skipping Steps in Calculation	Break down the problem into smaller steps and follow through each one methodically to avoid missing important details.
Rushing Through Exercises	Take your time with each question, double-check your work, and make sure every part of the problem is addressed.
Overlooking Units of Measurement	Always pay attention to units and convert them when necessary to ensure accurate results.
Failing to Check Results	After finding a solution, review each step to confirm its correctness and ensure no errors were made along the way.

Tips for Avoiding Mistakes

• Stay Organized: Keep your work neat and organized to minimize the chance of making small errors.
• Use Visual Aids: Draw diagrams or use models to help visualize problems, especially for geometry-related questions.
• Practice Regularly: The more familiar you become with different types of problems, the less likely you are to make simple mistakes.

By being mindful of these common mistakes and following these strategies, students can improve their accuracy and confidence in solving problems, leading to better results and a stronger grasp of the material.

Understanding Math Standards for Grade 3

In third-level education, students are introduced to a set of essential skills and concepts that form the foundation for their future learning. These guidelines outline the key areas of focus that are necessary for building a strong understanding of fundamental principles. Knowing these expectations helps both students and educators align their efforts to achieve mastery in critical areas of study.

Focus Area	Description
Number Operations	Understanding how to perform basic operations, including addition, subtraction, multiplication, and division with whole numbers and simple fractions.
Place Value and Number Patterns	Recognizing the value of digits in multi-digit numbers and identifying patterns to make calculations easier and faster.
Measurement and Data	Learning to measure length, weight, volume, and time, and understanding how to collect and interpret data using charts and graphs.
Geometry	Identifying shapes and understanding their properties, such as symmetry, perimeter, and area.
Problem Solving	Applying the learned concepts to solve real-world problems and making connections between different mathematical ideas.

These key areas provide a roadmap for student development, ensuring that learners gain a comprehensive understanding of foundational concepts. By focusing on these skills, students are better equipped to tackle more complex challenges as they progress in their education.

Strategies for Mastering Go Math Lessons

To achieve proficiency in core concepts, students need to develop effective strategies for tackling each lesson. Success comes from understanding key principles, staying organized, and applying a systematic approach to problem-solving. These strategies help students retain information and confidently handle challenges that come their way.

One of the most effective ways to master the material is to break down complex tasks into smaller, manageable steps. This approach makes it easier to digest and reduces the feeling of being overwhelmed. Additionally, reinforcing learned concepts through consistent practice helps to strengthen comprehension and retention.

Active participation in learning, whether through individual study or group work, is another crucial strategy. Engaging with the content, asking questions, and discussing solutions with peers or teachers can clarify doubts and improve understanding. It’s also important to review previous lessons regularly, as this reinforces knowledge and enhances long-term memory.

Visualization techniques, such as drawing diagrams or using models, can be extremely helpful in making abstract concepts more tangible. When dealing with word problems, interpreting the question and identifying the relevant information is key to applying the correct solution methods. Above all, patience and perseverance are essential. Each concept takes time to master, and consistent effort leads to improvement.

How the Answer Key Supports Learning

Having access to correct solutions is an essential tool for reinforcing learning. It allows students to verify their work, identify errors, and understand the reasoning behind each solution. This not only builds confidence but also enhances comprehension, helping students connect theoretical knowledge with practical application.

Immediate Feedback and Self-Assessment

By referring to the solutions, learners can immediately assess their understanding of the concepts. This instant feedback helps them identify any gaps in their knowledge and correct mistakes quickly, preventing misconceptions from solidifying. Self-assessment encourages students to reflect on their problem-solving process and make improvements where necessary.

Understanding the Problem-Solving Process

The solution guide provides more than just the final result–it highlights the steps taken to reach the answer. This is crucial for developing a deeper understanding of the problem-solving process. By reviewing these steps, students can learn different strategies and approaches that can be applied to similar challenges in the future.

Incorporating solutions as part of the learning process fosters a sense of autonomy in students. They can independently navigate through their mistakes and successes, ultimately strengthening their overall skill set. This encourages continuous growth and helps learners gain confidence in their abilities.

Benefits of Practicing with Go Math

Consistent practice is a fundamental part of mastering any subject, and it plays a crucial role in building confidence and improving problem-solving skills. Engaging with exercises that align with core concepts helps solidify foundational knowledge and prepares students to tackle more complex challenges. This approach encourages deeper understanding, strengthens retention, and enhances overall performance.

Benefit	Explanation
Reinforced Concept Mastery	Regular engagement with exercises helps to internalize essential concepts, making them second nature and easier to recall when needed.
Increased Confidence	Repetition builds confidence by allowing students to feel more comfortable with the material, reducing anxiety and promoting a positive learning experience.
Improved Problem-Solving Skills	Working through a variety of problems helps students develop critical thinking and analytical skills, enabling them to approach new challenges with greater ease.
Faster Learning Progression	As students become more proficient through regular exercises, they begin to grasp advanced concepts at a faster pace, accelerating their overall academic development.
Better Retention	Practice allows students to revisit and reinforce concepts periodically, aiding long-term retention and making it easier to apply knowledge in real-world scenarios.

By incorporating frequent practice into the learning process, students not only become more adept at solving problems but also develop a more comprehensive understanding of the material. The benefits of practice extend beyond simply achieving better grades–they foster lifelong learning habits and the ability to approach challenges with confidence and resilience.

How to Track Progress with Answer Key

Tracking progress is a vital part of the learning process, allowing students to evaluate their strengths and identify areas that need improvement. With the right tools, it’s easier to monitor advancement and adjust study strategies accordingly. Reviewing the provided solutions after completing exercises helps determine how well concepts are being grasped and where more attention may be required.

Evaluating Accuracy and Identifying Mistakes

By comparing their work with the provided solutions, learners can check for errors and understand why certain answers are incorrect. This immediate feedback highlights where mistakes are being made, allowing students to pinpoint specific areas where they may need more practice or a deeper understanding. Regularly assessing these discrepancies helps them learn from errors and avoid repeating them in the future.

Setting Learning Goals

Tracking progress also involves setting goals based on performance. After each round of exercises, students can identify which concepts they have mastered and which ones still need work. Setting measurable goals for improvement–such as mastering a certain skill or reducing mistakes in specific areas–provides motivation and direction. Revisiting these goals periodically ensures that learners stay on track and continue to advance steadily.

Using the solution guide as a tool for progress tracking enables learners to become more self-aware, helps to build confidence, and encourages a proactive approach to learning. With each review, students gain a better understanding of their learning journey and are better equipped to take the necessary steps to improve further.

Step-by-Step Solutions for Each Topic

Breaking down complex problems into manageable steps is essential for mastering any subject. By following clear, detailed instructions for each concept, students can understand the process behind the solution, rather than just memorizing the final result. This structured approach helps build a stronger foundation and promotes critical thinking, allowing learners to apply their knowledge to new challenges.

Guided Process for Understanding Concepts

Each topic can be approached by first understanding the underlying principles. By following a step-by-step breakdown, students can visualize how to tackle problems systematically. This method ensures that no part of the problem is overlooked and that each step contributes to the overall solution. With each step carefully explained, learners can internalize the process and replicate it independently.

Strengthening Problem-Solving Skills

Breaking down problems into smaller steps also enhances problem-solving abilities. As students work through each step, they not only learn the correct method but also gain insight into how to approach similar problems in the future. This strengthens their analytical skills and equips them with strategies to handle challenges across different topics.

Step-by-step solutions provide clarity and structure, making learning more accessible and effective. By following these detailed explanations, students can build confidence and develop a deeper understanding of the material, ensuring long-term academic success.

Improving Skills with Go Math

Enhancing skills in any subject requires consistent practice, focused strategies, and the right resources. By engaging with structured exercises, learners can build a strong foundation and develop their abilities over time. Whether through solving problems step by step or applying concepts in various scenarios, students can see measurable progress as they refine their approach and understanding.

Effective Strategies for Skill Enhancement

To effectively improve proficiency, it is important to adopt a few proven strategies that encourage deep understanding:

• Start with the Basics: Begin by mastering foundational concepts before moving on to more complex problems. This ensures that each new lesson builds on a solid understanding.
• Consistent Review: Regularly revisit previously learned material to reinforce knowledge and identify areas that may need additional focus.
• Apply Learning to Real-Life Situations: Practice applying what has been learned to real-world scenarios, which helps solidify skills and make the learning process more relevant.
• Work through Problems Systematically: Approach each problem in a structured manner, breaking it into smaller steps to better understand the process and reduce errors.

Tracking Progress and Success

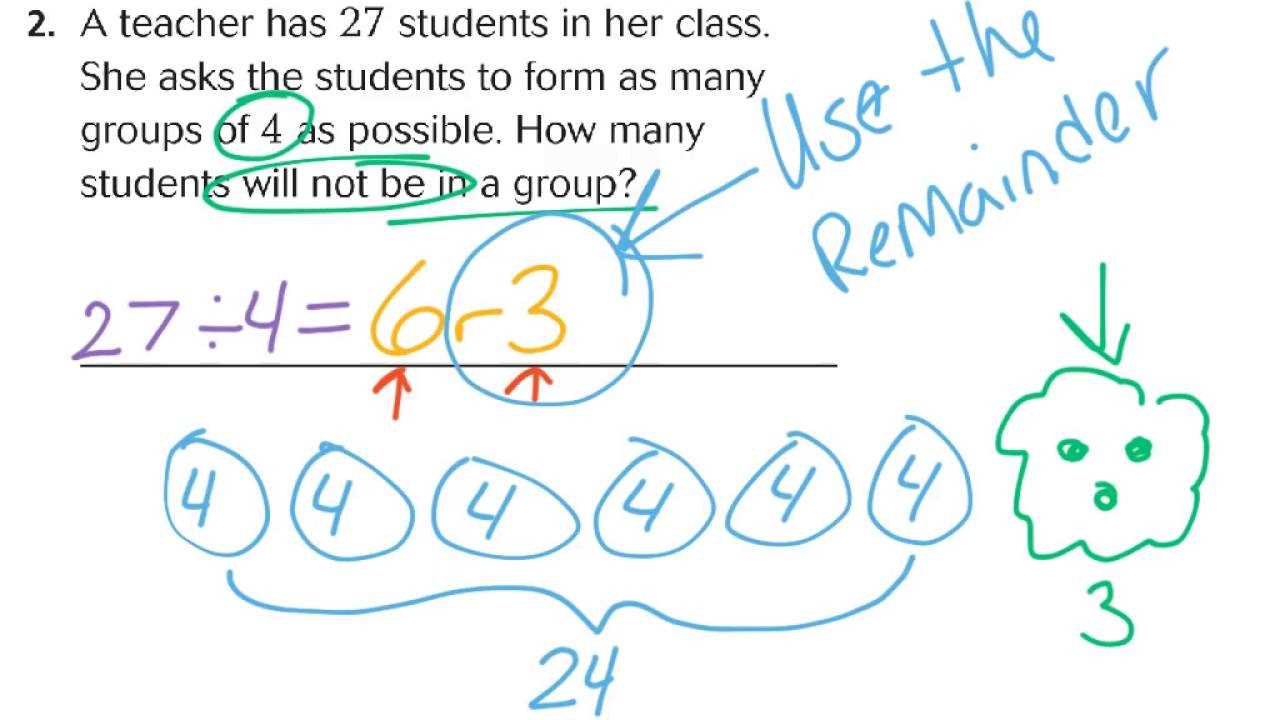
As students progress, it’s important to monitor their achievements and areas for improvement. Setting goals, reviewing progress regularly, and celebrating small victories can keep students motivated. Tracking performance allows learners to reflect on their strengths and identify areas that need further attention.

With dedication and the right approach, improving skills becomes an ongoing process of growth. By engaging with structured content and strategies, students can not only improve their performance but also build confidence in their abilities.

How to Review Mistakes in Go Math

Identifying and analyzing mistakes is a crucial part of the learning process. When errors are made, they present opportunities for improvement and deeper understanding. By systematically reviewing mistakes, students can pinpoint where their approach went wrong and how to correct it, ultimately leading to better results in future exercises.

Start by carefully looking at each mistake and understanding why it occurred. Was it a misinterpretation of the problem? A calculation error? Or perhaps a misunderstanding of a concept? By answering these questions, learners can isolate the root cause and take targeted action to avoid repeating the same mistakes.

Steps for Effective Mistake Review

Here are some steps to follow when reviewing errors:

• Revisit the Question: Reread the question carefully to ensure the problem was fully understood. Pay attention to key details and requirements.
• Check for Miscalculations: Double-check any calculations made during the process. Often, a simple misstep in arithmetic can lead to an incorrect result.
• Understand the Concept: If a concept was misunderstood, take time to review the relevant lesson or resources. Understanding the underlying principle is key to avoiding future mistakes.
• Practice Similar Problems: Once the mistake is identified, practice similar problems to reinforce understanding and build confidence.

Turning Mistakes into Learning Opportunities

Rather than feeling discouraged by errors, use them as tools for improvement. Keeping a record of frequent mistakes and tracking progress over time can provide valuable insights into areas that need more attention. Remember, every mistake is a chance to grow and develop a stronger grasp of the material.

Go Math vs Other Math Programs

When choosing a program to support learning, it’s essential to compare different options and understand their unique approaches. Each program offers a variety of methods and resources to help students grasp essential concepts. By understanding the strengths and weaknesses of different curricula, parents and educators can select the best fit for their students’ needs.

Go Math stands out for its structured approach, emphasizing problem-solving and critical thinking. However, it’s useful to compare it against other popular programs to assess how they cater to the learning needs of young learners.

Key Differences Between Go Math and Other Programs

Several aspects distinguish Go Math from other educational resources:

• Focus on Real-World Applications: Go Math often integrates real-life scenarios, encouraging students to apply learned concepts to practical situations. Other programs may focus more on abstract theory without connecting to everyday experiences.
• Interactive Learning: Go Math includes interactive elements like digital tools and online exercises, promoting a hands-on approach to learning. Many other programs, however, rely more heavily on textbooks and worksheets.
• Progressive Skill Building: Go Math follows a systematic progression, where students gradually build on prior knowledge. Some programs might present material in a more fragmented manner, making it harder for students to connect concepts.

What Other Programs Offer

Other educational curricula may emphasize different learning techniques:

• Traditional Methods: Many programs focus on rote learning, where students memorize facts and formulas, which can be helpful for certain learners but might not engage critical thinking as much.
• Hands-On Learning: Some programs place a greater emphasis on physical manipulatives or visual aids, helping students learn through tactile experiences, which can be beneficial for kinesthetic learners.
• Integrated Technology: While Go Math integrates technology through its digital tools, other programs may offer more immersive learning environments, such as gamified platforms or virtual tutoring sessions.

Ultimately, the best program depends on the individual learner’s preferences, strengths, and areas for growth. By comparing these options, educators and parents can ensure they select a curriculum that supports students’ development effectively.

Engaging Activities to Supplement Lessons

Enhancing the learning experience with engaging activities can make concepts more accessible and enjoyable for students. While structured lessons provide foundational knowledge, supplementary activities encourage active participation, creativity, and critical thinking. These activities allow students to apply what they’ve learned in a variety of fun and practical ways, deepening their understanding of key concepts.

Incorporating interactive exercises and games can be especially effective in reinforcing ideas. These activities promote problem-solving skills and encourage students to think outside the box while maintaining their interest in the subject matter.

Activity Ideas to Support Learning

Here are a few creative ways to supplement lessons:

• Interactive Games: Design games that reinforce specific concepts, such as matching games, puzzles, or digital quizzes that challenge students to solve problems quickly and correctly.
• Group Projects: Encourage collaboration through group assignments where students work together to solve a larger problem, such as creating a project, making a presentation, or performing an experiment.
• Hands-On Activities: Use everyday materials to demonstrate concepts, such as measuring ingredients for a recipe to teach measurement or creating graphs with real-world data.

Table of Suggested Activities

Activity	Description	Skills Developed
Math Bingo	A fun bingo game where students answer questions to fill out their cards.	Problem-solving, quick thinking
Puzzle Challenges	Students complete puzzles that require them to apply previously learned skills to solve.	Logic, critical thinking
Scavenger Hunt	A classroom or outdoor hunt where students look for objects related to the lesson theme.	Exploration, application of concepts
Creative Storytelling	Students create stories incorporating specific learning points, helping them connect abstract ideas to real-life situations.	Creativity, communication

These activities can not only reinforce key concepts but also spark enthusiasm for learning. By supplementing lessons with creative and interactive exercises, educators can foster a more engaging and dynamic learning environment that supports diverse learning styles and encourages a deeper connection with the material.

Preparing for Tests with Go Math

Effective preparation is crucial for performing well on assessments. With the right approach, students can build confidence and improve their problem-solving abilities. The key to successful test preparation lies in mastering the material, practicing skills, and developing strategies for approaching various question types. This process not only helps in achieving good test scores but also deepens overall understanding.

When preparing for an evaluation, reviewing previously learned concepts, identifying areas of weakness, and working on reinforcing those areas can make a significant difference. By using supplemental tools that align with the curriculum, students can approach tests with a clear strategy and the ability to tackle challenges efficiently.

Strategies for Effective Preparation

• Review Core Concepts: Start by revisiting the main ideas taught throughout the lessons. Understanding the foundational concepts is critical for solving complex problems.
• Practice with Sample Problems: Solve a variety of sample questions similar to those that may appear on the test. This helps students get comfortable with the format and the types of challenges they might face.
• Time Management: Simulate test conditions by practicing under time constraints. This teaches students to manage their time effectively and avoid rushing through questions.

Tracking Progress

Tracking progress is an essential part of test preparation. By regularly assessing strengths and weaknesses, students can focus their efforts on areas that require improvement. Keeping track of scores on practice tests and identifying patterns of mistakes will help in refining problem-solving strategies and enhancing test-taking skills.

Preparing for an assessment involves more than just reviewing information–it is about developing a mindset that helps students perform at their best. By combining targeted practice, time management, and progress tracking, learners will be ready to face any challenge confidently.

Where to Find Additional Resources

In order to supplement lessons and improve understanding, it is important to access a variety of resources beyond regular classroom materials. Whether you’re looking to deepen your knowledge of specific topics or seeking different approaches to problem-solving, there are many avenues to explore. Utilizing additional tools can provide a comprehensive understanding and support continued growth in the subject matter.

Various websites, platforms, and offline resources offer valuable content that aligns with educational objectives. These resources can range from interactive tutorials to detailed guides and exercises, ensuring a well-rounded educational experience. Whether you’re a student seeking extra help or a teacher looking for enrichment activities, there are plenty of options to explore.

Online Resources

• Interactive Learning Platforms: Websites like Khan Academy and IXL provide interactive lessons and practice activities for a wide range of topics, offering both free and paid options.
• Educational YouTube Channels: Many channels, such as Crash Course and Math Antics, provide clear explanations and engaging content that can help clarify complex ideas in a fun way.
• Printable Worksheets: Websites like Teachers Pay Teachers and Education.com offer a variety of printable worksheets that are designed to reinforce key concepts with hands-on practice.

Offline Resources

• Library Books: Many libraries carry educational books and guides on different subjects. These resources often include exercises, explanations, and examples that are useful for deepening understanding.
• Study Groups: Joining a study group or forming one with classmates can provide peer support and an opportunity to discuss difficult topics collaboratively.
• Tutoring Services: Local tutoring centers or online tutoring services offer personalized assistance for students who need additional help with specific concepts.

By exploring these additional resources, students can reinforce their learning, gain a deeper understanding of topics, and improve their overall academic performance. With access to both online and offline materials, there is no shortage of ways to enhance the educational experience.