
In the realm of mathematics education, the first step toward mastering concepts lies in having a clear understanding of problem-solving techniques. Whether you’re tackling complex equations or exploring logical patterns, having access to comprehensive support materials can significantly enhance your learning experience. This guide is designed to provide essential insights and resources for students seeking to reinforce their knowledge and build a solid foundation.
Learning and practice go hand in hand. By examining detailed explanations and following a systematic approach to solving various types of exercises, learners can improve their ability to think critically and solve challenges efficiently. The solutions provided here serve as a helpful reference to ensure that key principles are understood and applied correctly.
Through effective practice and careful analysis, students can strengthen their skills and gain confidence in their ability to handle more advanced topics. Whether you’re preparing for an exam or simply looking to improve your overall understanding, this guide offers the tools needed to succeed.
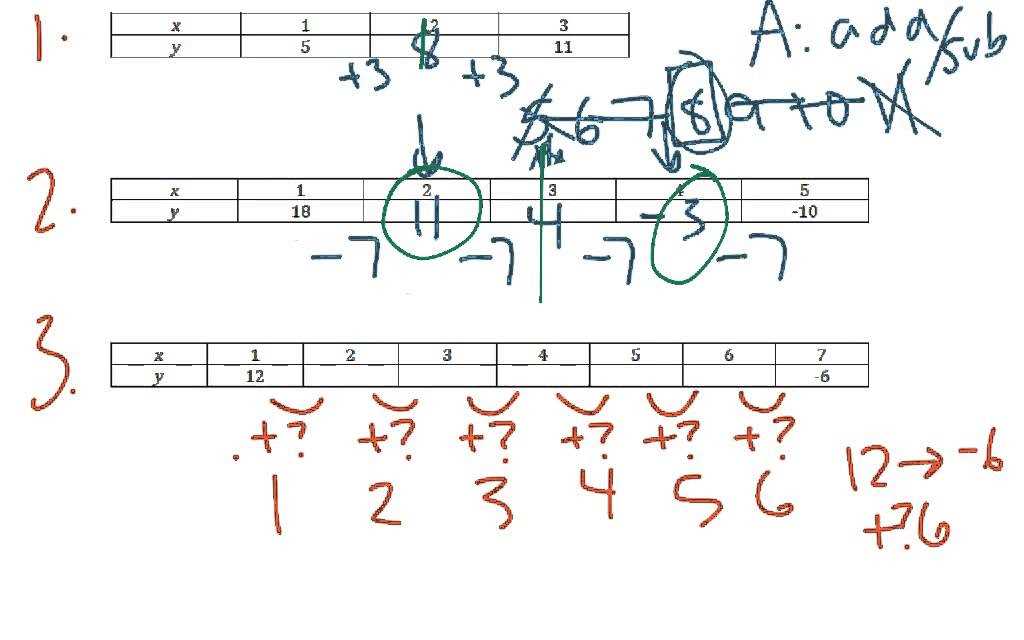
Mathematics Vision Project Module 1 Answer Key
In the learning process, understanding the steps and reasoning behind solving various problems is crucial for building a strong foundation. By reviewing carefully detailed solutions and methodologies, students gain insight into how to approach and solve complex exercises effectively. This section offers guidance that supports the application of essential techniques and ensures clarity when facing challenging problems.
The solutions provided here highlight the best practices for tackling key exercises. By analyzing the steps, students can see how to logically break down each question and reach the correct conclusion. This approach helps in strengthening both problem-solving skills and overall comprehension.
- Review step-by-step procedures to grasp core concepts.
- Understand the reasoning behind each solution to build critical thinking.
- Use the provided solutions as a reference for similar problems.
By following this guide, learners can refine their understanding of fundamental concepts and gain confidence in their ability to solve progressively difficult tasks. The resources presented here aim to equip students with the tools they need for academic success.
Overview of Mathematics Vision Project
This educational initiative aims to transform the way students engage with core mathematical concepts. By integrating practical problem-solving techniques with theoretical knowledge, the curriculum is designed to build critical thinking and analytical skills. The focus is on fostering deep understanding, encouraging exploration, and promoting active learning across a range of topics.
Focus on Conceptual Understanding
The program prioritizes a strong conceptual foundation, encouraging students to grasp the “why” behind mathematical principles, not just the “how.” This approach ensures that learners can apply their knowledge to real-world situations, strengthening both their practical and theoretical grasp of the subject.
Enhancing Problem-Solving Skills
Another key objective of the curriculum is to enhance students’ ability to tackle complex problems. By working through a variety of challenges, learners develop strategies for approaching problems with confidence and clarity. The goal is to cultivate a mindset that is adaptable and capable of addressing problems from multiple angles.
Importance of Module 1 in the Curriculum
The first section of the learning path plays a pivotal role in setting the foundation for more advanced topics. It is designed to introduce essential concepts and develop critical skills that will be built upon in later stages. By focusing on core principles and practical applications, this section ensures that students are well-equipped for the challenges ahead.
- Establishes fundamental knowledge that supports future learning.
- Fosters a deeper understanding of core techniques and methods.
- Helps students develop logical reasoning and problem-solving abilities.
By mastering the content of this initial stage, learners are able to approach more complex material with greater confidence and competence. This early mastery is crucial for both academic success and real-world application of the concepts learned.
How to Use the Answer Key
Having access to a comprehensive solution guide is an essential tool for reinforcing your understanding and improving problem-solving skills. It is not simply a resource for checking the correctness of your work, but a valuable guide that can help you understand the steps and reasoning involved in reaching the correct conclusion. Proper use of this resource can significantly enhance your learning process.
Step 1: Review Your Work First
Before consulting the solutions, attempt the problems independently. This practice will help identify areas where you may need further explanation or where your approach may require adjustment.
Step 2: Compare and Analyze
Once you’ve completed an exercise, refer to the solutions to compare your work. Focus on understanding the methods used to arrive at the answer. Pay attention to the logical steps taken and any specific techniques employed that you might have missed.
Step 3: Learn from Mistakes
If your solution differs from the guide, carefully analyze where the mistake occurred. Understanding why your approach was incorrect is just as important as understanding the correct approach. This reflection helps solidify your knowledge and improves your ability to solve similar problems in the future.
Step 4: Reinforce with Practice
Use the guide as a resource for repeated practice. The more you revisit problems and apply the correct methods, the more confident and proficient you will become in using the concepts you’ve learned.
Step-by-Step Problem Solving Approach
A systematic approach to tackling complex challenges ensures that problems are solved efficiently and effectively. By breaking down each problem into smaller, manageable steps, students can avoid feeling overwhelmed and focus on addressing each part methodically. This approach not only helps with accuracy but also enhances understanding by clarifying the logic behind each decision made during the process.
Understand the Problem
The first step is to clearly understand the problem at hand. Read through the question carefully, noting the key information and identifying what is being asked. Recognize any given values or constraints, and determine what is missing or needs to be solved. Clarifying these elements helps create a strong foundation for the next steps.
Plan and Solve
Once the problem is understood, plan your approach. Decide which techniques or methods are most appropriate for solving the problem. Break the problem into smaller steps, and apply the chosen strategies to solve each part. Always double-check intermediate results to ensure accuracy before proceeding to the next stage.
By following these steps, the process becomes more organized, reducing the likelihood of mistakes and allowing for a deeper understanding of the problem-solving methods employed.
Key Concepts Covered in Module 1
The first stage of the curriculum introduces a variety of essential principles that form the foundation for more advanced topics. These concepts focus on strengthening students’ understanding of core techniques, ensuring they have the necessary skills to tackle more complex challenges in the future. The focus is on building both conceptual clarity and practical application, enabling learners to approach problems with confidence.
Fundamental Techniques and Strategies
In this section, students are introduced to basic methods that are essential for solving problems efficiently. Mastering these techniques allows learners to approach various challenges with a clear, organized approach.
- Understanding relationships between numbers and variables.
- Applying systematic approaches to problem-solving.
- Using visual aids, such as graphs and charts, to represent data.
Critical Thinking and Logical Reasoning
Another major focus is on developing the ability to reason logically and make decisions based on available information. This helps students strengthen their critical thinking and improve their analytical skills.
- Breaking down complex problems into simpler steps.
- Identifying patterns and making connections between different concepts.
- Evaluating multiple approaches to solve a single problem.
These foundational concepts are designed to enhance overall mathematical understanding and create a solid base for more advanced studies.
Common Mistakes in Module 1
While learning new concepts, students often encounter challenges that can lead to common errors. These mistakes typically arise from misunderstandings or misapplications of fundamental principles. Identifying and addressing these errors early in the learning process can help build stronger problem-solving skills and ensure better overall understanding.
Misunderstanding Key Concepts
One of the most frequent mistakes is not fully grasping the core ideas before attempting more complex tasks. Without a clear understanding of the basics, it becomes difficult to apply those concepts correctly in different contexts.
- Confusing different mathematical operations–mixing up addition and subtraction or multiplication and division.
- Overlooking units or variables–failing to account for the correct units of measurement or misunderstanding the role of variables in equations.
- Assuming shortcuts without verification–jumping to conclusions without checking if each step logically follows the previous one.
Incorrect Application of Strategies

Another common mistake is misapplying problem-solving strategies or failing to follow a logical sequence of steps. This can result from rushing through tasks or neglecting to review all the necessary information before proceeding.
- Skipping intermediate steps–attempting to solve problems without fully understanding the process required for each step.
- Using inappropriate methods–applying strategies that are not suited to the particular problem type or context.
- Forgetting to check work–failing to double-check calculations and solutions can lead to avoidable mistakes.
By being aware of these common mistakes and taking the time to review the material carefully, students can avoid unnecessary errors and improve their overall comprehension and accuracy.
Understanding the Problem-Solving Strategies
Effective problem-solving involves using structured approaches to break down complex challenges into smaller, more manageable steps. By following a clear set of strategies, learners can tackle difficult problems with confidence and clarity. The goal is to identify the most appropriate method for each situation and apply it consistently for the best results.
Step-by-Step Breakdown
One key strategy is to divide the problem into smaller parts. This helps in organizing thoughts and ensures that no aspect of the problem is overlooked. By focusing on one step at a time, students can make steady progress and reduce the chances of making errors.
Identifying Patterns
Another effective strategy is recognizing patterns or similarities with previously solved problems. This allows for the reuse of known solutions or approaches, saving time and effort. Patterns can often provide shortcuts that simplify the problem-solving process.
Logical Deduction and Reasoning
Problem-solving also relies heavily on logical reasoning. This involves drawing conclusions based on evidence and known facts, and eliminating incorrect possibilities. Using logical deduction helps ensure that each step in the process is grounded in solid reasoning.
By mastering these strategies, students improve their ability to approach challenges systematically, leading to more efficient and effective problem resolution.
Tips for Mastering Module 1 Content
To truly master the content in the initial section, it’s essential to approach the material with a focused and disciplined mindset. Success comes from not just completing the exercises but fully understanding the concepts behind them. Below are some practical tips to help strengthen your grasp on the subject and set a strong foundation for future learning.
Practice Consistently
Consistent practice is one of the most effective ways to solidify your understanding. Repetition helps reinforce concepts and improves retention. Set aside dedicated time each day to work through problems, and make sure to revisit topics you find challenging. Regular practice builds confidence and sharpens problem-solving skills.
Seek Clarification When Needed
It’s important to ask questions and seek clarification when you’re unsure about a concept. Don’t wait until confusion builds up–address doubts immediately. You can refer to additional resources, ask a peer, or consult an instructor for help. Understanding every step of the process is crucial to mastering the content.
By following these tips, you’ll not only increase your understanding of the material but also develop stronger problem-solving abilities that will serve you in more advanced topics.
Assessment of Module 1 Learning Outcomes
Evaluating how well learners have understood the material covered is crucial for identifying areas of strength and those that need further development. Assessments allow both students and instructors to measure progress, ensuring that key concepts have been fully grasped. A well-structured assessment helps guide future learning and can pinpoint specific topics for review.
Methods of Evaluation
There are various ways to assess the understanding of the content, each focusing on different aspects of learning. Common methods include quizzes, problem-solving tasks, and reflective exercises, which test both comprehension and application of concepts.
| Assessment Method | Purpose | Skills Tested |
|---|---|---|
| Quizzes | Measure knowledge retention and recall | Memory, comprehension |
| Problem-Solving Tasks | Test the ability to apply concepts in practice | Application, critical thinking |
| Reflection Exercises | Encourage deeper understanding and analysis | Self-assessment, analytical thinking |
Interpreting the Results
Once the assessment is complete, it’s important to analyze the results to understand learning gaps. High scores indicate a strong grasp of the material, while lower scores highlight areas for review. Regular assessments ensure continuous improvement and reinforce the foundational concepts that are essential for progressing to more complex topics.
Why Module 1 is Crucial for Success
The first section of any learning journey lays the foundation for everything that follows. Mastery of the core concepts introduced early on is essential for long-term success, as they serve as the building blocks for more advanced material. Understanding the fundamental ideas thoroughly ensures that students are prepared to tackle increasingly complex challenges with confidence.
Foundational Knowledge and Skills
The early lessons are not just introductory–they are vital for establishing the essential skills and knowledge needed for all subsequent topics. A solid grasp of these concepts helps learners approach new material with greater ease and reduces the likelihood of struggles later in the course.
| Key Concept | Importance | Impact on Future Learning |
|---|---|---|
| Basic Problem-Solving Techniques | Provides methods for tackling new challenges | Essential for applying more advanced strategies |
| Conceptual Understanding | Helps form connections between ideas | Supports deeper learning in future topics |
| Critical Thinking | Fosters analytical thinking and reasoning | Encourages effective decision-making in complex problems |
Building Confidence for Advanced Topics
When students master the initial content, they feel more confident as they progress. Success in the first section often leads to a more positive attitude toward learning, as students develop the belief that they can overcome challenges. This confidence is crucial when approaching more difficult topics, as it encourages persistence and a proactive mindset.
Challenges Students Face in Module 1
While the initial section of any course is designed to introduce foundational concepts, it can also present a variety of challenges for students. These challenges often arise from unfamiliarity with the material, difficulty grasping new techniques, or struggles with applying theoretical knowledge in practical situations. Identifying these obstacles early is essential for overcoming them and ensuring continued progress.
One common difficulty students face is understanding abstract concepts that may feel disconnected from real-world applications. For some learners, this can make the content seem daunting or irrelevant. Another challenge is the transition from passive learning to active problem solving, which requires not only knowledge but also critical thinking and analytical skills.
Additionally, students often encounter problems when trying to connect new ideas with prior knowledge. Without a clear understanding of how these concepts build on one another, it becomes difficult to see the bigger picture and apply the material effectively. These hurdles can hinder the learning process if not addressed properly.
How to Improve Your Math Skills
Enhancing your abilities in this subject requires a combination of consistent practice, understanding underlying concepts, and applying problem-solving techniques. Improvement doesn’t come overnight, but with dedication and the right strategies, you can build a strong foundation and gain confidence in tackling complex problems.
Effective Study Techniques
To make steady progress, it’s important to incorporate the following methods into your study routine:
- Practice Regularly: The more problems you solve, the more familiar you will become with different types of questions and approaches.
- Understand Concepts: Focus on truly grasping the fundamental principles behind each problem, rather than memorizing formulas.
- Break Problems into Steps: Tackling a large problem by dividing it into smaller, manageable parts can help you approach it systematically.
- Seek Help When Needed: Don’t hesitate to ask for assistance from a tutor, peer, or online resources if you’re struggling with specific topics.
Building Confidence through Practice
Confidence comes with practice and perseverance. As you become more familiar with the material, you’ll notice that solving problems becomes easier. The key is not to get discouraged by initial struggles–every challenge is an opportunity to learn and grow.
Teacher’s Guide to Module 1 Answer Key
This section is designed to assist educators in effectively guiding students through the initial section of the course. By utilizing a detailed reference guide, teachers can provide better support to learners, help them navigate complex problems, and ensure they understand the core concepts being introduced. A structured approach to teaching is essential for fostering a deeper understanding and a positive learning experience.
How to Use the Reference Guide
Educators can use this reference guide in several ways to enhance classroom instruction:
- Provide Clear Explanations: Use the guide to clarify key concepts and common problem-solving strategies, ensuring that students understand both the “how” and “why” behind each step.
- Offer Targeted Support: Identify areas where students typically struggle and focus on those sections during class discussions or one-on-one sessions.
- Encourage Independent Practice: Encourage students to first attempt problems on their own, then refer to the guide for self-checking and additional clarification.
- Monitor Progress: Use the reference to track each student’s understanding and identify any persistent areas of difficulty.
Common Pitfalls and How to Address Them
It’s important to be aware of the common challenges students face in this section and know how to effectively address them:
- Misunderstanding Core Concepts: If students are confused about the foundational ideas, take time to revisit these areas using different teaching methods, such as visual aids or hands-on examples.
- Difficulty with Application: Encourage students to practice applying concepts in various contexts to strengthen their problem-solving skills.
- Lack of Confidence: Some students may hesitate to attempt problems independently. Providing positive reinforcement and gradual challenges will help build their confidence over time.
Using the Answer Key Effectively for Practice
Utilizing a reference guide for self-study can significantly improve understanding and mastery of complex concepts. Rather than simply looking at the solutions, it is essential to approach the material strategically to maximize learning. By following a structured process, students can not only check their work but also deepen their comprehension of the underlying principles.
Steps to Use the Guide for Effective Practice
Here are some practical steps to follow when using a reference guide to enhance your practice:
- Attempt Problems First: Always try to solve problems on your own before consulting the guide. This helps reinforce critical thinking and problem-solving skills.
- Compare Your Solution: After attempting the problem, review the solution in the guide. Check for accuracy and ensure that you understand the reasoning behind each step.
- Identify Gaps in Understanding: If your solution differs from the guide, take the time to understand where your thought process went wrong. Focus on those specific areas to build a stronger foundation.
- Revisit Difficult Problems: Rework problems you find challenging, using the guide as a tool for clarification and further practice. Repetition helps to solidify concepts.
- Test Yourself Without Assistance: Once you feel confident, try solving problems without referring to the guide. This will help evaluate how well you’ve internalized the material.
Common Mistakes to Avoid When Using the Guide
While the reference guide is a valuable tool, there are some common pitfalls to avoid to ensure it is used most effectively:
- Relying Too Much on the Guide: Constantly checking the guide after every step can hinder independent thinking. Use it as a backup, not a crutch.
- Skipping Over the Steps: It’s essential to not only check the final solution but also review each step to ensure a complete understanding of the process.
- Overlooking Small Mistakes: Small errors can often lead to bigger misunderstandings. Pay attention to detail and correct even minor mistakes to avoid developing bad habits.
Advanced Tips for Excelling in Module 1
Achieving mastery in complex topics requires more than basic understanding. To excel, students must apply advanced strategies that promote deep learning and critical thinking. These tips are designed to enhance problem-solving abilities and ensure long-term retention of the material. By integrating these techniques, learners can tackle even the most challenging problems with confidence.
Effective Study Habits for Advanced Learners
Building effective study habits is crucial for excelling in any learning process. Here are some advanced techniques for refining your study routine:
| Tip | Benefit | How to Implement |
|---|---|---|
| Active Recall | Enhances memory retention and reinforces understanding. | After reading a concept, test yourself on the material without referring to notes. |
| Spaced Repetition | Prevents forgetting by reinforcing learning over time. | Review concepts periodically at increasing intervals. |
| Teach What You Learn | Helps clarify concepts and strengthens retention. | Explain complex topics to others or teach them out loud to yourself. |
| Contextual Learning | Links theoretical knowledge with practical applications. | Relate new concepts to real-world situations or personal experiences. |
Critical Problem-Solving Strategies
To truly master the subject, applying critical problem-solving strategies is essential. These approaches go beyond the basics, helping learners tackle problems efficiently and creatively:
- Break Down Complex Problems: Divide larger problems into smaller, more manageable parts. This makes it easier to identify patterns and apply solutions.
- Work Backwards: Starting from the end result can sometimes offer clearer insights into how to approach the problem, especially in calculation-heavy tasks.
- Use Multiple Approaches: Approach problems from different angles. If one method doesn’t work, try an alternative approach to find a solution.
- Analyze Mistakes Carefully: After encountering a mistake, understand why the error occurred. Identifying the root cause ensures that the