Mathematics Vision Project Module 3 Answer Key Guide

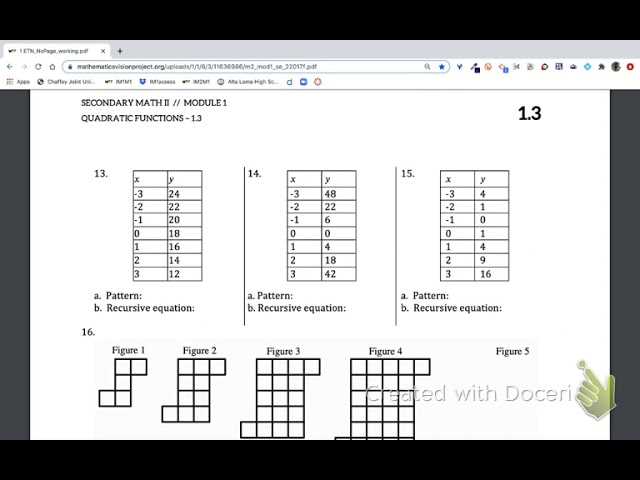
In the realm of advanced learning, mastering key topics is crucial for academic growth and proficiency. This section is designed to provide learners with the necessary resources to navigate through complex problems and strengthen their skills. The focus is on enhancing comprehension and ensuring that every step in the learning process is clear and achievable.

To excel, it is important to develop a systematic approach to solving exercises. By following a structured path, students can not only improve their problem-solving abilities but also gain a deeper understanding of the underlying principles. This guide will offer insights and solutions that serve as valuable aids, helping to clarify challenging concepts and provide clear directions for learners.

With the right tools and strategies, learners can approach any topic with confidence, ensuring that each hurdle becomes an opportunity for growth. This resource is intended to empower individuals, enabling them to engage with the content more effectively and develop a comprehensive understanding of the subject matter.

Mathematics Vision Project Overview

This learning initiative is designed to enhance students’ problem-solving abilities and critical thinking skills. It offers a comprehensive curriculum aimed at fostering a deeper understanding of core mathematical concepts through structured, step-by-step exercises. The primary goal is to equip learners with the tools necessary to approach complex tasks with confidence and clarity.

Core Principles of the Curriculum

Focus on conceptual understanding rather than rote memorization.
Emphasis on real-world applications and problem-solving skills.
Development of mathematical reasoning and logical thinking.
Encouragement of collaborative learning and peer interaction.

Learning Approach

The approach centers on presenting challenges that are both engaging and thought-provoking. Each exercise builds upon previous knowledge, encouraging students to explore concepts from different perspectives. The curriculum integrates both individual and group activities, fostering a balanced learning environment that supports diverse learning styles.

Individual tasks focus on personal mastery of topics.
Collaborative activities promote discussion and teamwork.
Hands-on problem-solving exercises strengthen comprehension.

Understanding Module 3 Concepts

This section focuses on deepening your comprehension of essential concepts that form the foundation for advanced problem-solving in the subject. It covers critical topics that require both theoretical understanding and practical application. By mastering these concepts, students can build a solid base to tackle more complex challenges with confidence.

Key Ideas and Principles

Grasping the relationship between different mathematical elements.
Understanding how abstract concepts are applied in real-world scenarios.
Developing the ability to break down problems into smaller, manageable parts.
Recognizing patterns and relationships within data sets.

Approaching Problems Effectively

When tackling exercises within this section, it is crucial to approach each problem methodically. Breaking down the problem, identifying key variables, and applying the correct strategies will lead to more accurate solutions. The process encourages logical thinking and helps learners stay organized throughout the problem-solving journey.

Start with identifying the key information in each problem.
Use diagrams or visual aids to clarify concepts where needed.
Apply relevant techniques to solve each step sequentially.

Key Objectives of Module 3

The purpose of this section is to ensure that learners acquire a deep understanding of fundamental principles, enabling them to approach increasingly complex problems with clarity and precision. Through targeted learning goals, this section emphasizes both conceptual mastery and the application of problem-solving techniques to real-life scenarios. By achieving these objectives, students will be prepared to progress to higher levels of study with a solid foundation.

Primary Learning Goals

Enhance ability to analyze and interpret complex problems.
Strengthen logical reasoning and critical thinking skills.
Apply learned strategies to solve real-world tasks.
Develop a structured approach to problem decomposition.

Skills Developed

Throughout this section, learners will refine skills necessary for tackling challenging tasks. These include identifying key information, selecting the appropriate methods, and systematically solving problems. The focus is on building confidence in applying theoretical knowledge to practical situations.

Improving precision in mathematical reasoning.
Building resilience when solving difficult problems.
Expanding understanding of abstract concepts through hands-on practice.

Step-by-Step Problem Solving Approach

A methodical approach to solving challenges is crucial for developing a clear understanding of complex topics. By breaking down each problem into manageable steps, learners can identify key concepts, apply the right techniques, and reach a solution in a systematic way. This process helps avoid errors and ensures that each step contributes to the overall solution.

Steps to Solve Problems Effectively

Read and Understand: Begin by carefully reading the problem to identify what is being asked. Ensure you understand all the variables involved.
Identify Key Information: Extract the important data points or relationships that are essential to solving the problem.
Plan a Strategy: Decide which methods or formulas are needed to tackle the problem. Break the task down into smaller parts.
Execute the Plan: Carry out each step, applying the chosen methods and keeping track of the calculations.
Review the Solution: Once the problem is solved, check the work for any errors and ensure the solution makes sense in the context of the question.

Tips for Success

Always double-check the initial assumptions to ensure accuracy.
Visual aids like diagrams or graphs can simplify complex problems.
Break down larger problems into smaller, more manageable tasks.
Review any mistakes to learn from them and improve future problem-solving.

Benefits of the Answer Key

Having access to a comprehensive guide for solving problems brings significant advantages for learners. It acts as a valuable tool for verifying calculations, confirming the correctness of solutions, and gaining insights into different problem-solving techniques. By reviewing the provided solutions, students can identify areas of strength and weakness, fostering improvement and a deeper understanding of the concepts involved.

Improved Understanding and Efficiency

Clarifies the correct approach to complex tasks.
Helps reinforce the learning process by reviewing each step.
Facilitates quicker identification of mistakes, allowing for more efficient correction.
Serves as a useful reference for future exercises.

How it Supports Learning Progress

The solution guide not only helps in completing exercises correctly but also contributes to long-term academic growth. It offers students the opportunity to reflect on their work, compare their approach to the suggested one, and understand the reasoning behind each step.

Benefit	Explanation
Confidence Boost	Provides assurance that the solutions are accurate and that the methods used are effective.
Time-Saving	Speeds up the learning process by quickly identifying errors and correcting them without wasting time.
Enhanced Conceptual Clarity	Deepens understanding by showing the correct application of techniques and concepts.

How to Use the Answer Key Effectively

While having a guide to check your solutions is valuable, it is essential to use it in a way that enhances your understanding rather than simply relying on it for quick fixes. Proper utilization of a solution guide can lead to better comprehension, improved problem-solving skills, and a more thorough grasp of the concepts involved. The key is to approach it as a learning tool, not just a way to confirm results.

Step-by-Step Review Process

Work through the problem independently first to engage your thinking process.
Once you have your solution, compare it with the provided steps to ensure accuracy.
If your solution differs, review each step to identify where the error occurred.
Understand why the correct method works and how it applies to similar problems.
Use the guide to reinforce the concepts rather than memorizing answers.

Common Mistakes to Avoid

Relying on the guide before attempting the problem yourself.
Using the solution to skip over important steps in the process.
Not reflecting on why the provided solution works the way it does.
Overlooking patterns or techniques that could help in future exercises.

Common Mistakes in Module 3 Exercises

When working through exercises, students often make errors that can hinder their understanding of the material. These mistakes can stem from misinterpreting the problem, skipping steps, or overlooking key concepts. Recognizing and addressing these common pitfalls is essential to improving performance and building a solid grasp of the material. By being aware of these typical mistakes, learners can avoid them and refine their problem-solving skills.

Common Mistake	Explanation	How to Avoid
Misreading the Problem	Rushing through the question can lead to missing important details.	Carefully read the problem and underline key information before starting.
Skipping Steps	Jumping directly to the solution without breaking the problem into smaller steps can lead to errors.	Work through each part methodically, ensuring no step is overlooked.
Incorrect Application of Methods	Using the wrong technique or formula for a given problem can lead to incorrect results.	Double-check the method required for each problem and ensure it’s applied correctly.
Overlooking Units or Labels	Forgetting to consider units or labels can lead to mismatched or incorrect answers.	Always note the units and labels for every calculation, and ensure they match throughout.
Failing to Verify the Solution	Not reviewing the final answer for logical consistency and accuracy.	After solving, always recheck the solution and ensure it aligns with the original question.

How Module 3 Builds Mathematical Skills

This section is designed to enhance critical thinking and problem-solving abilities by focusing on a range of core concepts. By engaging with progressively challenging tasks, learners not only deepen their understanding but also develop the necessary skills to approach new and unfamiliar problems. The exercises are structured to foster a methodical approach to problem-solving, helping students refine their logical reasoning and analytical skills.

Through a combination of guided practice and real-world application, students are encouraged to think strategically and work through problems step by step. This process reinforces essential skills, such as identifying patterns, formulating strategies, and applying mathematical principles to practical situations. As learners progress, they gain the confidence and expertise needed to tackle more advanced concepts.

The approach emphasizes active learning, where students gain hands-on experience and reinforce their knowledge by applying it to different contexts. By focusing on key skills and gradually increasing the difficulty level of the exercises, the section ensures that students are well-equipped to build on their foundation and continue developing their problem-solving abilities.

Strategies for Module 3 Success

Achieving success in this section requires a combination of effective strategies that not only help students complete exercises but also deepen their understanding of the material. By developing a strong approach, learners can improve their problem-solving skills and boost their overall performance. The key is consistency, focus, and a structured method of tackling each problem step by step.

One of the most important strategies is breaking down complex tasks into smaller, manageable parts. This allows students to understand the underlying principles more clearly and avoid feeling overwhelmed. Additionally, reviewing each step thoroughly and identifying common mistakes can significantly enhance learning. Regular practice and self-assessment are also crucial in mastering the concepts.

Strategy	Description	Benefits
Break Down Problems	Divide complex problems into smaller sections to understand each part clearly.	Helps reduce overwhelm and provides a clearer understanding of the process.
Review Mistakes	After solving a problem, go over it again to identify any errors or misunderstandings.	Fosters better retention and prevents the same mistakes from happening in the future.
Practice Consistently	Regularly work through problems to strengthen knowledge and build confidence.	Improves familiarity with concepts and increases efficiency over time.
Ask for Help	If stuck, seek clarification from a teacher, tutor, or peer to ensure correct understanding.	Encourages deeper understanding and provides alternative explanations when necessary.
Use Visual Aids	Incorporate diagrams, charts, or graphs to visualize the problem.	Helps make abstract concepts more tangible and easier to comprehend.

Exploring Key Formulas in Module 3

This section highlights essential equations and expressions that are central to solving the problems in this area. Understanding these formulas is crucial for building a strong foundation in mathematical reasoning and problem-solving. Each formula serves as a tool to approach and simplify complex tasks, allowing students to apply proven methods effectively. Grasping the underlying principles behind these formulas not only helps in completing exercises but also fosters a deeper comprehension of the subject as a whole.

Important Equations to Remember

Linear Equation: A foundational concept that represents relationships with a straight line. Example: y = mx + b, where m is the slope and b is the y-intercept.
Quadratic Formula: Used to solve second-degree equations. Example: x = (-b ± √(b² – 4ac)) / 2a, where a, b, and c are the coefficients of the equation.
Area and Perimeter of Shapes: These formulas help calculate the area and perimeter of geometric figures such as rectangles, triangles, and circles.

Applications of Formulas in Real-Life Situations

Problem Solving: Using the right formula allows you to break down complex problems into manageable parts, making it easier to arrive at a solution.
Modeling Real-World Situations: Many real-life scenarios, such as financial planning, engineering, and physics, can be modeled using the appropriate formulas, making them invaluable tools beyond the classroom.
Checking Work: Once a formula is applied correctly, it serves as a verification tool to ensure that the results are accurate.

Answer Key for Practice Problems

This section provides solutions to the practice exercises, offering a comprehensive guide to understanding how each problem can be tackled effectively. By reviewing these solutions, learners can confirm their approach, identify any mistakes, and improve their problem-solving strategies. It’s an essential resource for reinforcing the concepts learned and gaining confidence in applying them to similar challenges.

Solutions to Common Problems

Problem 1: Given a set of linear equations, find the value of x. The solution follows the step-by-step process of isolating variables and applying the correct operations.
Problem 2: A geometric shape’s area is determined using the standard formula, ensuring that dimensions are correctly substituted into the equation.
Problem 3: Solving for the unknown in a quadratic equation involves applying the quadratic formula and simplifying each step to find the roots.

How to Use the Provided Solutions

Step-by-Step Review: Carefully compare your method with the provided solutions to ensure you are following the correct procedures.
Identify Mistakes: If your results differ from the solutions, identify where the mistake occurred and correct it.
Practice Regularly: Use the solutions to practice similar problems, strengthening your understanding and refining your approach to solving challenges.

Real-World Applications of Module 3

The concepts and skills explored in this section are not only essential for academic success but also have practical applications in various fields. Understanding how to apply these principles can lead to solutions for real-world problems, ranging from everyday calculations to complex engineering challenges. By linking theoretical knowledge with practical use, learners gain a deeper understanding of how to make informed decisions based on mathematical reasoning.

Applications in Engineering and Architecture

In fields like engineering and architecture, the ability to apply formulas and problem-solving strategies is crucial. For example, calculating material requirements, determining structural integrity, and designing efficient systems all rely heavily on the concepts explored in this section. Whether it’s calculating the dimensions of a building or optimizing a mechanical design, the skills developed here are directly applicable to real-world challenges.

Finance and Budgeting

In finance, understanding the principles of equations and functions plays a key role in areas such as budgeting, investments, and financial planning. By using the correct formulas, individuals and organizations can accurately forecast costs, calculate interest rates, and analyze financial data. These skills help professionals make sound financial decisions, whether for personal or corporate finance.

Everyday Problem Solving

Budget Management: Using basic mathematical models to track expenses, savings, and investments.
Travel Planning: Applying calculations to determine travel time, cost, and routes for optimal planning.
Home Improvements: Estimating materials and costs required for DIY projects, ensuring efficiency and budget adherence.

How Module 3 Prepares for Future Topics

The foundation built in this section serves as a stepping stone for more advanced concepts encountered in later studies. By mastering the essential techniques and strategies introduced here, learners develop the critical thinking and problem-solving skills necessary to tackle more complex topics in the future. This preparation ensures that students are not only ready to progress but also able to integrate new knowledge seamlessly with their existing understanding.

Building Problem-Solving Strategies

As learners progress, the ability to approach problems methodically becomes increasingly important. The skills developed in this section provide the tools needed to break down more intricate challenges into manageable steps. These strategies are essential for tackling higher-level topics, such as algebraic manipulation, calculus, and statistical analysis, where a logical, step-by-step approach is key.

Strengthening Conceptual Understanding

By mastering the concepts presented here, students build a solid understanding that will be required in more advanced fields. Topics such as systems of equations, functions, and geometric proofs rely heavily on the foundational knowledge established in this section. The practice and repetition ensure that learners are not only familiar with these ideas but are also able to apply them fluently in new and varied contexts.

Comparing Different Versions of the Answer Key

In this section, we explore various versions of the solution guides available for reference. These versions may differ in terms of clarity, depth of explanation, or even the presentation format. By comparing these different versions, learners can gain a more comprehensive understanding of the material and choose the guide that best suits their learning style and needs.

Detailed Explanations vs. Brief Solutions

One of the key differences between the available guides is the level of detail provided. Some solutions offer a step-by-step breakdown with in-depth explanations for each stage of the problem, which can be especially helpful for learners who need more guidance. On the other hand, more concise versions provide only the necessary steps, which may appeal to those who prefer a quicker reference or are already familiar with the underlying concepts.

Format Differences: Written vs. Visual

Another important distinction lies in the format of the solutions. Some guides focus on written instructions, while others incorporate visual aids such as diagrams or flowcharts. Visual learners may benefit from seeing problems solved with the help of illustrations, whereas others may prefer a text-based approach for a more straightforward explanation of the solution process.

Additional Resources for Module 3

To enhance your understanding and mastery of the concepts covered, several supplementary materials are available. These resources offer different types of support, from practice exercises to detailed explanations, helping learners tackle challenges and deepen their knowledge. Below are some valuable tools and references to complement your study.

Online Platforms and Tutorials

Khan Academy: A vast collection of instructional videos and practice problems that cover a wide range of topics, providing clear explanations and step-by-step solutions.
Coursera: Offers courses and specializations from top universities, often with interactive elements to enhance learning.
Brilliant.org: A problem-solving website focused on developing deeper conceptual understanding through interactive challenges.

Books and Study Guides

“Problem Solving Strategies” by Arthur Engel: A comprehensive guide on how to approach complex problems with structured methodologies.
“The Art of Problem Solving” series: Highly recommended for students looking for in-depth practice and advanced techniques in problem-solving.

Practice Worksheets and Exercises

IXL: An interactive learning platform offering thousands of practice problems that cover various topics in detail.
Wolfram Alpha: A powerful computational tool for verifying solutions and exploring alternative approaches to problems.

These resources are designed to work together with your current studies, reinforcing core concepts and expanding your problem-solving abilities. Be sure to explore different formats and find the ones that suit your preferred learning style.

Tips for Mastering Module 3

Achieving proficiency in the concepts covered in this section requires a combination of consistent practice, strategic thinking, and a solid understanding of fundamental principles. By approaching the material methodically, you can strengthen your skills and build confidence in solving complex problems. Below are some key strategies to help you excel in this area.

Focus on Understanding Concepts, Not Just Procedures

It’s essential to grasp the core ideas behind each problem-solving technique rather than memorizing steps. Understanding why a particular method works will enable you to apply it to different situations with greater ease. Spend time reviewing the theory behind each concept and try to explain it in your own words to ensure a deeper comprehension.

Practice Regularly and Diversify Your Exercises

Consistent practice is one of the most effective ways to reinforce what you’ve learned. Make sure to work through a variety of problems, as this will expose you to different types of challenges and help you develop a flexible problem-solving approach. Don’t hesitate to revisit topics you find difficult and practice those areas until you feel confident.

Use Visual Aids and Resources

Visualizing problems can often provide new insights and simplify complex tasks. Utilize diagrams, charts, and graphs to help break down problems into more manageable components. Additionally, online platforms, tutorials, and textbooks can offer alternate perspectives that might resonate better with your learning style.

Review and Reflect on Mistakes

After completing practice problems, take the time to review your mistakes and understand why the solutions didn’t work. This process of reflection helps identify gaps in your understanding and provides an opportunity to refine your problem-solving techniques. Consider seeking guidance from peers, instructors, or online communities if you’re having trouble with specific challenges.

By following these tips and maintaining a disciplined approach, you’ll improve your ability to tackle problems efficiently and build a strong foundation for more advanced topics in the future.