In this section, we will explore a range of solutions to challenging mathematical problems that require a deeper understanding of core concepts. The aim is to provide clarity and enhance your problem-solving skills by breaking down complex exercises into manageable steps.
Each problem is accompanied by clear explanations, highlighting essential techniques and strategies. By the end of this guide, you will be better equipped to tackle similar challenges with confidence, applying the methods learned in practical scenarios.
Effective problem-solving requires both knowledge and practice. This guide will help reinforce the concepts that underpin each solution, offering insight into how to approach various mathematical questions systematically and efficiently.
Mathematics Vision Project Module 6 Answer Key
This section offers a detailed breakdown of solutions to complex exercises that require a deeper grasp of mathematical principles. By analyzing each problem, you can enhance your understanding and improve your ability to solve similar challenges in the future.
Key Problem Solving Strategies
Each solution is crafted with the aim of providing a clear and structured approach. The key is to identify the core concepts involved and apply relevant techniques to arrive at the correct results.
Common Approaches and Methods
The following table outlines common approaches used to solve typical problems within this section. Each technique is explained with respect to the steps involved and the rationale behind the method.
| Problem Type | Solution Approach | Key Concept |
|---|---|---|
| Algebraic Equations | Solving for variables | Linear Equations |
| Geometric Proofs | Using logical deductions | Geometry Theorems |
| Probability Calculations | Applying probability rules | Combinatorics |
By following these techniques, learners can systematically tackle each problem while developing a stronger foundation in the concepts they represent.
Overview of Module 6 Content
This section provides an in-depth look at the content covered in the sixth part of the curriculum, focusing on advanced concepts and problem-solving techniques. It introduces learners to a variety of mathematical principles and challenges designed to enhance their understanding and skills.
The topics presented here explore a wide range of concepts, from algebraic expressions to geometric proofs and statistical analysis. Each concept is presented in a way that builds upon previous knowledge, allowing for a deeper and more comprehensive understanding of the subject matter.
Throughout this section, learners will encounter a variety of exercises that aim to strengthen their critical thinking abilities. These problems encourage the application of learned techniques in real-world contexts, fostering both analytical and practical skills.
Key Concepts in Module 6
This section focuses on the essential principles that form the foundation of the exercises and problems within this part of the curriculum. Understanding these fundamental ideas is crucial for solving complex problems and applying mathematical techniques effectively.
Among the core concepts explored are algebraic manipulation, geometrical reasoning, and probability theory. Each area is designed to build on previous knowledge, enhancing the learner’s ability to approach more advanced topics with confidence.
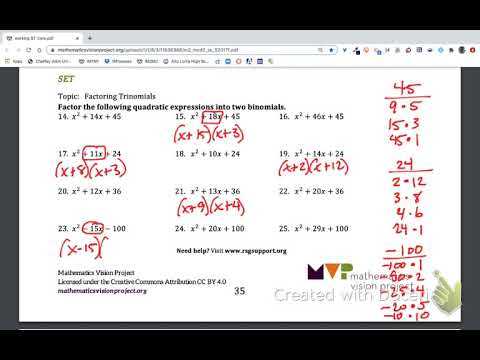
Algebraic manipulation involves simplifying expressions and solving equations using various methods, such as factoring and substitution. Geometrical reasoning emphasizes logical proofs and the application of geometric theorems to solve problems. Finally, probability theory teaches the principles of predicting outcomes in uncertain situations, using combinatorics and probability laws.
Step-by-Step Problem Solving Guide
In this section, we will break down the process of tackling complex exercises into a clear and systematic approach. By following each step, you can develop a structured way to solve challenging problems and enhance your critical thinking skills.
Understanding the Problem
The first step is to thoroughly read and comprehend the problem. Identify the key information and what is being asked. Take note of any given data or conditions, as they will guide the solution process.
Formulating a Strategy
Once the problem is understood, devise a plan to approach it. This may involve selecting appropriate mathematical methods, such as equations, logical reasoning, or applying relevant formulas. Break the problem into smaller, more manageable parts if necessary.
Execution is the next critical step, where you apply the chosen strategy to solve each component of the problem, ensuring that each step is completed accurately. Finally, verify your solution by reviewing the steps to ensure the results are consistent with the given conditions and make logical sense.
Understanding Mathematical Strategies in Module 6
This section explores essential techniques and approaches designed to solve complex problems effectively. By mastering these strategies, learners can tackle various challenges with confidence and precision.
The following list outlines some of the core methods employed in problem-solving:
- Breaking Down Problems: Simplify complex tasks by dividing them into smaller, manageable steps.
- Identifying Patterns: Recognize recurring themes or relationships to simplify solutions.
- Logical Reasoning: Use structured thinking to deduce unknown values or relationships.
Additional strategies that support accurate problem-solving include:
Common Mistakes to Avoid
When tackling complex problems, it’s easy to make errors that can derail the entire solution process. Recognizing and avoiding these common mistakes is essential to achieving accurate and consistent results.
One frequent error is rushing through the problem without fully understanding all the given information. This often leads to misinterpretations or missed details that are critical to the solution. Take the time to carefully read and analyze the problem before proceeding.
Another common mistake is skipping steps or overlooking intermediate calculations. Every step in the problem-solving process is important, even if it seems insignificant. Skipping over details can cause the final result to be incorrect.
Lastly, failing to double-check your work is a critical mistake. Even after arriving at a solution, it is vital to review your process and results to ensure everything aligns logically. Mistakes can often be identified during this final step of verification.
Tips for Mastering Module 6
Achieving success in this section requires both practice and a solid understanding of the core concepts. By applying the following strategies, you can enhance your skills and tackle problems with greater ease and confidence.
Practice regularly: The more problems you solve, the more familiar you will become with the techniques and methods required. Consistent practice helps reinforce concepts and improves problem-solving speed.
Understand the theory: It’s important to grasp the underlying principles behind each concept. Don’t just memorize formulas–focus on understanding how and why they work. This deeper knowledge will make solving complex problems easier.
Break problems into smaller parts: Large problems can often feel overwhelming. Break them down into manageable steps, focusing on one part at a time. This approach allows for better clarity and helps avoid mistakes.
Seek help when needed: If you encounter difficulties, don’t hesitate to ask for assistance. Whether from peers, instructors, or additional resources, clarifying confusing points early on can save you time and effort in the long run.
How to Approach Module 6 Exercises
Successfully completing exercises in this section requires a thoughtful and strategic approach. By following a structured method, you can work through each problem with clarity and efficiency, ensuring that you don’t overlook important steps.
Start by carefully reading the problem to identify key information and any constraints. Understanding what is given and what needs to be found is the foundation of solving the exercise. Take note of important numbers, relationships, or conditions provided in the problem.
Step 1: Break Down the Problem
Once you have grasped the essential details, break the problem into smaller, manageable parts. This will allow you to tackle each component individually, making the task less overwhelming. By isolating each step, you reduce the chances of making errors and improve your focus.
Step 2: Apply Relevant Techniques
Next, apply the appropriate strategies or formulas based on the nature of the exercise. Whether it’s algebraic manipulation, geometric reasoning, or logical deduction, use the method that aligns best with the problem at hand. This step ensures that you are following a clear path towards finding the solution.
Lastly, after solving the problem, always double-check your work. Review the steps you took, the calculations you made, and ensure that the final result makes sense in the context of the question.
Solutions for Complex Problems Explained
This section provides detailed explanations of how to approach and solve challenging exercises. By breaking down complex problems into manageable steps, you can gain a deeper understanding of the processes involved and develop more effective problem-solving strategies.
For each difficult problem, we will explain the thought process behind each solution. This includes identifying the necessary information, selecting the appropriate techniques, and executing each step carefully to ensure accuracy. Below is an example of how to approach a complex problem:
Step-by-Step Breakdown
- Understand the problem: Identify what is given and what is required. Look for any hidden relationships or constraints that will guide your solution.
- Choose the right approach: Select the appropriate strategy based on the type of problem. Whether it’s solving an equation, analyzing a pattern, or using geometry, pick the method that best fits the situation.
- Work through the steps: Break the problem down into smaller, logical steps. Tackle each part individually to avoid mistakes.
- Verify your solution: After completing the problem, review your solution to ensure it is correct. Double-check calculations and ensure the result makes sense.
Practical Example
Let’s take a more complex problem involving multiple steps. For example, solving a system of equations might involve substitution or elimination. You would start by isolating variables, substituting known values, and solving for the unknowns. Each step must be done carefully to ensure accuracy.
By practicing this step-by-step method, learners can improve their ability to tackle even the most complex exercises with confidence and precision.
Importance of Practice in Module 6
Mastering complex concepts and developing problem-solving skills require consistent practice. Repeatedly working through exercises reinforces understanding and helps solidify techniques, making it easier to approach even the most challenging tasks with confidence.
Practice enables learners to become familiar with various approaches, allowing them to identify the most efficient methods for solving different types of problems. By tackling a range of exercises, individuals not only enhance their skills but also build a deeper understanding of underlying principles.
Furthermore, regular practice helps improve accuracy and speed. With each attempt, learners become more adept at spotting patterns, avoiding mistakes, and streamlining their process. Over time, this leads to increased confidence and proficiency, essential for tackling increasingly difficult problems.
Breaking Down Key Formulas
Understanding important formulas is crucial for solving complex problems effectively. Breaking them down into their individual components allows for a deeper understanding of how they work and how they can be applied in different situations. Rather than simply memorizing, focusing on the meaning behind each formula leads to better retention and flexibility in problem-solving.
Key formulas often contain variables that represent specific quantities, and understanding how these elements interact is essential. By analyzing each part of the formula and knowing when and how to use it, you can approach problems more strategically.
For example, in a formula involving distance, speed, and time, each variable plays a distinct role. Breaking the formula into steps and understanding the relationships between the variables helps you apply it correctly in various contexts.
How to Use the Answer Key Effectively
Using a solution guide properly is an essential part of mastering problem-solving techniques. It is a helpful resource, but it should be treated as a tool for learning, not a shortcut. To gain the most from it, focus on understanding the steps and reasoning behind each solution instead of simply copying the answers.
First, try solving the problem on your own. Afterward, refer to the guide to compare your approach and results. Pay close attention to any differences in methodology or reasoning. This practice helps you identify areas where your understanding may need improvement and refine your techniques for future problems.
Step 1: Attempt the Problem Independently
Before checking any solutions, try solving the problem on your own. This allows you to actively engage with the material and gives you a clear picture of where you might need further clarification or practice. Even if you make mistakes, it’s an important part of the learning process.
Step 2: Compare and Analyze the Solution
Once you have attempted the problem, use the solution guide to check your work. Compare each step carefully and ask yourself why the approach used in the guide works. This comparison allows you to see different problem-solving strategies and ensures you are not just memorizing steps, but understanding the reasoning behind them.
By following these steps, you will be able to maximize the value of the solution guide and strengthen your overall understanding of the material.
Real-Life Applications of Module 6 Concepts
The concepts explored in this section have wide-ranging applications in real-world scenarios. By understanding the foundational principles, you can apply them in various fields, from engineering and economics to everyday problem-solving. These principles are not only theoretical but are integral to solving practical challenges across different industries.
Below are some examples of how these concepts can be applied in real life:
| Field | Application | How the Concepts are Used |
|---|---|---|
| Engineering | Designing Efficient Systems | Optimization techniques help engineers design systems that maximize efficiency while minimizing cost and resources. |
| Economics | Market Analysis | Understanding trends and making predictions using statistical models aids in making informed economic decisions. |
| Technology | Software Development | Algorithms and problem-solving strategies are applied to enhance software functionality and performance. |
| Medicine | Medical Imaging | Mathematical models assist in creating detailed images of the human body for diagnostic purposes, aiding in treatment planning. |
As these examples show, the practical applications of these concepts are vast and important in many aspects of modern life. Mastery of these techniques provides a strong foundation for making informed decisions and improving processes in a variety of fields.
Guidelines for Self-Assessment
Evaluating your own understanding and progress is a crucial part of the learning process. Self-assessment helps identify areas of strength and areas that need improvement. By regularly reflecting on your performance, you can adjust your study strategies and improve your skills more effectively.
Steps for Effective Self-Assessment
- Review the Material: Go through your notes, exercises, and solutions to refresh your memory on key concepts.
- Test Your Understanding: Try to solve problems independently without looking at the solutions. This will help you gauge your mastery of the concepts.
- Check for Mistakes: Look for any errors in your work. Mistakes can offer valuable insights into areas that need more attention.
- Compare with Examples: Compare your solutions with provided examples or correct answers to check if your approach and results are consistent.
- Seek Feedback: If possible, discuss your solutions with peers or mentors to get external perspectives on your work.
Key Aspects to Focus On
- Conceptual Understanding: Ensure you fully grasp the core ideas before moving to more complex tasks.
- Problem-Solving Skills: Pay attention to how you approach each problem and if there are more efficient methods you could use.
- Accuracy and Precision: Double-check your calculations and reasoning to ensure that everything is correct.
- Time Management: Track how much time you spend on each task to improve your efficiency in solving future problems.
By following these guidelines, you can develop a deeper understanding of the material and enhance your learning experience. Self-assessment is not only about finding errors, but also about recognizing progress and gaining confidence in your abilities.
Exploring Advanced Topics in Module 6
In this section, we delve into more sophisticated concepts that build on the foundational ideas explored earlier. These advanced topics require a deeper understanding and the ability to apply concepts in a variety of contexts. Mastering these areas will not only enhance your problem-solving skills but also improve your ability to tackle complex challenges.
As you progress, it’s essential to approach these advanced concepts with patience and persistence. They often involve multiple steps and interrelated ideas, so a systematic approach is key. By breaking down the material into manageable parts and continuously reinforcing your understanding, you will be better equipped to handle intricate problems.
Advanced topics may involve the application of theory to real-world scenarios, deeper exploration of abstract principles, or the introduction of more complex mathematical techniques. These topics are designed to stretch your thinking and enhance your ability to think critically and creatively in problem-solving situations.
Preparation for Upcoming Modules
As you advance through your studies, it’s crucial to prepare for the next stages of learning. Anticipating the concepts and skills that will be covered in the upcoming lessons will help you approach new material with confidence. The key to success in future topics is building a strong foundation and ensuring that you have mastered the current content before moving on.
In order to effectively prepare for future lessons, consider reviewing your notes, solving practice problems, and reinforcing your understanding of foundational principles. These steps will allow you to move seamlessly into more complex subjects and make the learning process smoother and more enjoyable.
Setting a Solid Foundation
Start by revisiting key concepts from previous lessons. Focus on understanding the underlying principles and how they connect to the new topics you will encounter. The more thoroughly you grasp these foundational ideas, the easier it will be to tackle advanced concepts.
Active Learning Strategies
Engage in active learning by solving problems, discussing concepts with peers, or applying theories to real-world situations. This hands-on approach will enhance your retention and deepen your understanding of the material, ensuring you are well-prepared for what comes next.
Resources for Further Learning
To deepen your understanding and continue developing your skills, it’s essential to explore additional materials beyond the core lessons. Supplementing your studies with extra resources can provide new perspectives, clarify complex concepts, and help reinforce your knowledge. These tools will empower you to approach challenging topics with confidence and expertise.
Here are several valuable resources that can support your learning journey:
- Textbooks and Reference Books: Find detailed explanations, worked-out examples, and practice problems to enhance your comprehension of fundamental and advanced topics.
- Online Courses and Tutorials: Many platforms offer free or paid courses that guide you through concepts step-by-step, with video lectures and interactive exercises.
- Interactive Learning Platforms: Websites and apps that offer quizzes, flashcards, and problem-solving tools to test your knowledge in real-time.
- Study Groups and Forums: Join online or in-person study groups to collaborate with others, discuss topics, and seek help from experienced peers.
- Practice Workbooks: Focus on problem-solving with dedicated practice books that cover a wide variety of exercises to reinforce what you’ve learned.
By exploring these resources, you can extend your knowledge beyond the standard curriculum, strengthening your skills for more complex challenges ahead.