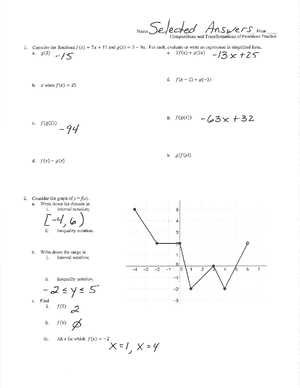
For students looking to enhance their problem-solving abilities, having access to structured resources can significantly improve understanding and performance. These tools offer a step-by-step guide to tackling various topics, ensuring that key concepts are grasped thoroughly and correctly. They help clarify complex ideas and provide a pathway for consistent progress in understanding mathematical principles.
Solutions play a crucial role in the learning process, serving as a reference for verifying the accuracy of calculations and approaches. They allow learners to identify where they may have made errors, offering opportunities for correction and deeper comprehension. By engaging with these resources, students can build confidence and improve their ability to solve even the most challenging problems.
Effective use of such learning aids goes beyond simply matching the results; it encourages reflection on the methods used and fosters critical thinking. Understanding how to arrive at the correct solution through logical steps is just as important as knowing the final answer itself. These tools promote mastery by encouraging both independent problem-solving and guided learning from mistakes.
Mathematical Learning Tools for Problem Solving
In any learning process, having reliable resources that provide guidance is essential for mastering new concepts. These tools offer detailed support, enabling learners to understand their mistakes and enhance their problem-solving strategies. They serve as a valuable asset for anyone aiming to refine their skills and deepen their understanding of various topics in the field of mathematics.
How These Resources Help Students
These guides are not just about providing correct results, but also about offering a structured approach to solving problems. By reviewing the provided steps and methods, students can better understand the reasoning behind each solution. This process of comparison and analysis improves critical thinking, which is key to mastering the subject.
Developing Stronger Problem-Solving Skills
Utilizing such tools encourages a deeper engagement with the material. By reviewing the different steps outlined in each solution, students can refine their techniques and apply them to new problems. This active learning process strengthens their ability to independently solve complex problems and build a strong foundation for future topics.
Understanding the Mathematics Vision Project
This initiative aims to provide a comprehensive approach to learning, focusing on enhancing problem-solving skills and conceptual understanding. The resources developed are designed to help students engage with complex ideas and break them down into manageable steps. By doing so, learners can build a strong foundation in various topics and improve their ability to solve problems efficiently.
The materials emphasize active learning and self-reflection. Learners are encouraged to explore different strategies and understand the reasoning behind each method. This encourages a deeper connection with the subject and equips students with the tools they need to tackle challenging problems.
Core Features of the Initiative
- Structured lessons that build from basic to advanced concepts
- Clear explanations and step-by-step guides for solving problems
- Opportunities for independent practice and skill reinforcement
- Feedback mechanisms to help identify and correct mistakes
How It Enhances Learning

- Fosters critical thinking by encouraging students to analyze different methods of solving problems.
- Helps students develop confidence in their abilities through consistent practice and guidance.
- Promotes a deeper understanding of complex ideas by breaking them down into understandable parts.
Overview of Secondary Math 2 Curriculum
The curriculum for this level is designed to deepen students’ understanding of key concepts and enhance their ability to apply mathematical reasoning in various contexts. It focuses on developing skills that are essential for tackling more advanced topics and real-world problems. The lessons are structured to build on prior knowledge while introducing new techniques and strategies for solving complex problems.
Throughout this course, students are encouraged to explore a range of topics, from algebraic expressions to geometric reasoning. The goal is to create a strong foundation that will support further study in higher-level subjects. This approach emphasizes logical thinking and problem-solving skills, preparing learners for future challenges both in and outside the classroom.
Core Topics Covered
- Algebra: Solving equations and inequalities
- Linear functions and their applications
- Geometric reasoning and properties of shapes
- Statistics and probability
- Quadratic equations and their graphing
Key Learning Outcomes
- Mastery of algebraic techniques and problem-solving methods
- Improved understanding of geometric concepts
- Ability to apply learned principles to real-life scenarios
- Confidence in approaching advanced topics in higher education
Importance of Answer Keys in Learning
Having access to solution guides is an essential part of the educational process. They provide learners with the opportunity to check their work, identify mistakes, and understand the correct methods for solving problems. This feedback loop is vital for reinforcing learning and helping students develop a deeper understanding of the subject matter.
Solution guides not only provide the correct results but also clarify the steps required to reach them. By comparing their own work with the solutions, students can pinpoint errors in their approach and gain insight into more effective techniques. This process encourages self-reflection and improvement, key components of mastery.
Benefits of Using Solution Guides
- Clarification of Methods: Understanding the correct approach is just as important as getting the right result.
- Building Confidence: Verifying answers and methods helps learners feel more confident in their abilities.
- Encouraging Independent Learning: Using guides to assess their own work promotes greater independence and critical thinking.
How Solution Guides Support Long-Term Success
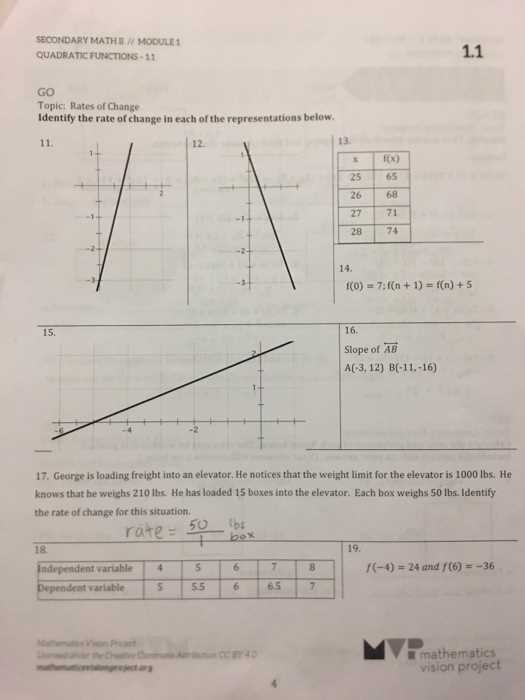
- They reinforce concepts by providing multiple opportunities for practice and error correction.
- They help learners build a solid foundation, preparing them for more advanced topics.
- They foster a growth mindset by showing that mistakes are part of the learning process and can lead to improvement.
How to Use the Answer Key Effectively
Using solution guides effectively goes beyond simply checking answers. It’s a tool for learning, helping you understand the methods behind the solutions and identify areas where improvement is needed. By actively engaging with these resources, you can enhance your problem-solving abilities and develop a deeper understanding of the material.
Rather than just verifying if an answer is correct, focus on comparing the steps you took to the provided solutions. This process of analysis allows you to recognize any gaps in your reasoning and refine your approach to similar problems in the future.
Steps for Effective Use
- Review Step-by-Step: Carefully examine each step in the solution to ensure you understand the logic behind it.
- Compare Your Methods: Check how your approach differs from the one presented in the guide.
- Identify Mistakes: If your result differs, try to pinpoint where your reasoning went wrong.
- Understand the Process: Focus on grasping the reasoning behind each step, not just memorizing the final answer.
Additional Tips for Improvement
- Use the solution guide as a tool for self-assessment and reflection after each problem.
- Rework problems from scratch once you understand the correct approach.
- Ask yourself how you can apply the same methods to different types of problems.
Key Concepts Covered in Secondary Math 2
This level of study focuses on building a deeper understanding of essential mathematical concepts. The curriculum introduces students to a wide range of topics that are critical for mastering advanced problem-solving techniques. Key ideas from algebra, geometry, and data analysis are explored in-depth to help learners develop the necessary skills for both academic success and real-world applications.
By the end of this course, students are expected to have a solid grasp of these fundamental concepts, which serve as the foundation for higher learning in mathematics. These concepts are not only valuable for future studies but also for practical problem-solving in daily life.
Core Topics in the Curriculum
| Topic | Description |
|---|---|
| Linear Equations | Solving and graphing linear equations and inequalities. |
| Functions | Understanding and analyzing various types of functions, including linear and quadratic. |
| Geometry | Exploring geometric shapes, their properties, and solving related problems. |
| Statistics | Collecting, analyzing, and interpreting data using basic statistical methods. |
| Quadratics | Working with quadratic equations, graphing parabolas, and applying real-world problems. |
Skills Developed in the Course
- Enhanced ability to solve algebraic and geometric problems.
- Improved understanding of functions and their applications.
- Stronger reasoning skills for approaching complex problems.
- Ability to analyze and interpret statistical data effectively.
Common Mistakes to Avoid in Math 2
During the learning process, it’s easy to fall into certain traps that can hinder progress. Being aware of common errors and actively avoiding them can help students improve their understanding and performance. These mistakes often stem from a lack of attention to detail, misunderstanding concepts, or rushing through problem-solving steps without proper analysis.
By identifying these mistakes early on, learners can take steps to correct them and strengthen their skills. Developing a thoughtful and careful approach to each problem is key to overcoming these challenges and excelling in more advanced topics.
Frequent Errors in Problem Solving
- Misunderstanding Problem Requirements: Not fully reading and understanding what the question asks can lead to incorrect solutions.
- Rushing Through Calculations: Skipping steps or making quick, careless mistakes during calculations can result in incorrect answers.
- Neglecting to Check Work: Failing to verify the solution after completing the steps can allow small errors to go unnoticed.
- Overlooking Negative Signs: Missing or incorrectly applying negative signs is a common mistake, especially in algebraic operations.
- Confusing Different Types of Functions: Not recognizing the differences between linear, quadratic, and exponential functions can lead to incorrect methods being used.
How to Avoid These Mistakes
- Read Carefully: Always take time to understand the problem before attempting to solve it.
- Break Down Each Step: Work through problems step by step, ensuring accuracy in each part of the process.
- Review Work: Double-check your final answers to catch any overlooked errors or miscalculations.
- Understand Core Concepts: Make sure to grasp the key principles and techniques before applying them to more complex problems.
Strategies for Solving Math 2 Problems
Approaching problems systematically and strategically is key to solving them effectively. Having a clear plan can help break down complex tasks into manageable steps, leading to more accurate solutions. By applying proven techniques and understanding the underlying principles, students can improve their problem-solving skills and build confidence in tackling challenging questions.
Whether working with algebraic expressions, geometric concepts, or data analysis, using the right strategies can significantly enhance problem-solving efficiency and accuracy. The following methods are highly effective when facing various types of questions in this level of study.
Effective Problem-Solving Methods
- Understand the Problem: Carefully read the problem and identify what is being asked. Take note of key information and determine what concepts are involved.
- Break the Problem Down: Split complex problems into smaller, more manageable parts. Solve each part step by step to avoid feeling overwhelmed.
- Choose the Right Approach: Based on the problem type, select the appropriate method, such as substitution, factoring, or graphing. Using the correct approach ensures efficiency and accuracy.
- Draw Diagrams: For geometry-related questions, sketching a diagram can provide a visual aid, helping to clarify relationships and make calculations easier.
- Double-Check Your Work: After solving a problem, review your steps and the final result. This helps catch any potential mistakes before finalizing your answer.
Additional Tips for Success
- Practice Regularly: Consistent practice reinforces concepts and improves fluency in solving different types of problems.
- Stay Organized: Keep track of your work neatly and in order, which helps prevent confusion during the problem-solving process.
- Ask for Help: If you encounter difficulties, don’t hesitate to ask for clarification or guidance from a teacher or peer.
How the Answer Key Supports Problem Solving
When tackling complex problems, having a resource to check progress and validate solutions can be immensely helpful. A detailed guide that provides the final solutions, along with step-by-step explanations, ensures that learners can track their understanding and pinpoint areas that may require more attention. This resource acts as both a tool for verifying correctness and a learning aid to deepen comprehension.
Using this tool wisely can enhance problem-solving skills by offering insights into how problems are structured and solved. It provides the opportunity for students to compare their methods with correct approaches, thereby reinforcing their learning process.
How the Resource Helps Clarify Steps
| Feature | Benefit |
|---|---|
| Step-by-Step Solutions | Guides students through each stage of the problem-solving process, showing how to apply different techniques correctly. |
| Clear Explanations | Explains the reasoning behind each step, helping students understand the logic rather than just memorizing steps. |
| Examples of Similar Problems | Provides additional problems with solutions, allowing learners to practice similar scenarios and reinforce their understanding. |
Benefits for Developing Problem-Solving Skills
- Improved Accuracy: Ensures that solutions align with the correct methods, preventing misunderstandings and mistakes.
- Enhanced Understanding: Demonstrates how to apply concepts in different contexts, improving overall comprehension.
- Self-Assessment: Helps students evaluate their progress and identify areas that need more attention or practice.
Improving Your Math Skills with Answer Keys
To enhance your problem-solving abilities, it is essential to have a reliable resource to guide your learning process. A comprehensive guide that offers correct solutions and detailed explanations can serve as a powerful tool in improving understanding and building confidence. By comparing your approach with well-structured solutions, you can identify mistakes, clarify concepts, and reinforce learning.
Using such a resource thoughtfully allows you to gain a deeper understanding of how each step in a problem should be approached. Rather than just checking answers, these guides provide insights into the methodology, enabling you to apply learned techniques in new situations.
How Using a Guide Enhances Skills
| Strategy | Benefit |
|---|---|
| Step-by-Step Guidance | Helps you understand the correct process for solving problems, reinforcing learning and minimizing mistakes. |
| Highlighting Mistakes | Allows you to see where errors occurred, helping to correct and avoid them in future problems. |
| Practice with Examples | Provides opportunities to practice similar problems, ensuring that you can apply concepts correctly in various scenarios. |
By regularly reviewing your work with this kind of resource, you build a stronger foundation of knowledge and improve your problem-solving techniques. It transforms the learning process into an interactive, self-correcting experience that nurtures a deeper understanding of mathematical concepts.
Different Methods for Checking Your Work
When solving complex problems, it is essential to have a variety of strategies to ensure the solutions are accurate. Checking your work is a critical step that allows you to confirm your calculations, verify the logic, and spot potential errors. By using multiple methods, you can strengthen your understanding and build confidence in your results.
There are several approaches to checking your work that can be applied depending on the type of problem you are solving. These methods help you confirm that each step is correct and that the final outcome is reliable. Here are some effective ways to ensure accuracy:
Common Techniques for Verifying Solutions
- Reversing the Process: Solve the problem in reverse to see if you arrive at the original question. This method helps confirm the validity of your solution.
- Using Alternative Methods: Try a different approach or formula to solve the same problem. If both methods lead to the same result, it increases the likelihood of correctness.
- Estimation: Make an educated guess about the solution before solving. Once you complete the problem, check if the final answer is close to your estimate. This can be particularly useful for complex calculations.
- Cross-Checking with Resources: Refer to guides or previously solved examples to compare your work and ensure consistency with known solutions.
By incorporating these strategies into your problem-solving routine, you can improve your ability to detect mistakes and refine your solutions. Practicing these methods regularly leads to better accuracy and a deeper understanding of the concepts you are working with.
How to Handle Challenging Math Problems
Confronting difficult problems can be a daunting task, but with the right approach, it becomes easier to navigate through them. Breaking down complex questions into smaller, manageable steps is key to overcoming obstacles. Rather than feeling overwhelmed, a structured approach can help you make steady progress and reach the correct solution.
When faced with a challenging problem, it is important to remain calm and methodical. The first step is to thoroughly understand the problem and identify what is being asked. From there, you can break it down into parts and tackle each one individually. There are several strategies that can help you overcome difficult problems efficiently.
Steps for Tackling Difficult Problems
- Read and Analyze Carefully: Take time to read the problem thoroughly. Highlight key information and ensure you fully understand what is being asked before proceeding.
- Identify Known and Unknown Variables: Make a list of what is given in the problem and what needs to be determined. This can help clarify the approach to take.
- Break Down the Problem: Divide the problem into smaller, simpler steps. Solve each part individually, and then combine the results for the final solution.
- Try Alternative Methods: If one method doesn’t seem to be working, try another approach. Different strategies can lead to the same outcome and may provide clarity.
- Check Your Work: Once you have completed the problem, review your steps and final solution. Make sure everything is logical and consistent.
Stay Confident and Patient
While challenging problems may seem frustrating, persistence and practice are key to improving your problem-solving skills. With each difficult question, you will build your ability to approach problems with confidence and flexibility. Remember, every problem solved is a step forward in mastering the concepts.
The Role of Practice in Mastering Math
Achieving proficiency in any subject requires consistent effort and practice, and this is especially true for problem-solving skills. Mastery comes with repeated engagement, allowing you to internalize concepts and refine techniques over time. The more you practice, the more familiar and intuitive the processes become, ultimately leading to greater confidence and understanding.
Regular practice helps reinforce the strategies and steps needed to tackle complex problems. It helps identify patterns, highlights common mistakes, and provides opportunities for improvement. By working through different types of problems repeatedly, learners can solidify their skills and gain a deeper grasp of the underlying principles.
Benefits of Consistent Practice
- Strengthens Problem-Solving Skills: Repeated exposure to different problem types enhances your ability to quickly identify solutions and apply techniques effectively.
- Increases Retention: The more frequently you engage with content, the more likely you are to retain and recall relevant information when needed.
- Builds Confidence: Success in solving problems builds self-assurance, enabling you to approach future challenges with a more positive mindset.
- Improves Efficiency: Practice makes the process smoother and faster, allowing you to complete tasks in less time while maintaining accuracy.
Practical Tips for Effective Practice
- Start with Simple Problems: Begin with easier questions to build your foundation, then progressively tackle more challenging ones.
- Track Progress: Keep a record of the problems you’ve solved and the areas you find most difficult, so you can focus on improving specific skills.
- Review Mistakes: Learning from errors is crucial. Analyze where you went wrong to avoid repeating the same mistakes in the future.
- Set Regular Practice Sessions: Consistency is key. Set aside dedicated time for practice each day or week to build a solid routine.
Through consistent and deliberate practice, you not only improve your technical skills but also develop a deeper understanding of how to approach different types of problems. The more you engage with the material, the better equipped you’ll be to handle future challenges with ease.
Using the Answer Key for Self-Assessment
Self-assessment is a crucial part of the learning process. It allows learners to gauge their understanding, identify areas of strength, and pinpoint topics that require further attention. Using a solution guide can serve as an effective tool in this process, providing a reference to check one’s work and evaluate problem-solving methods.
By comparing your approach to the solutions provided, you can identify where you made errors, and more importantly, understand why these mistakes occurred. This reflection not only helps correct misconceptions but also reinforces the correct procedures, enhancing your overall comprehension.
Benefits of Self-Assessment with Solutions
- Identifying Mistakes: Checking your results against provided solutions enables you to spot errors that might have been overlooked during the initial attempt.
- Clarifying Concepts: If the solution provided differs from your method, it’s an opportunity to reexamine the concept and approach the problem from a different angle.
- Building Confidence: Seeing that you’ve correctly solved a problem boosts your confidence and motivates further learning.
- Improving Understanding: Repeatedly reviewing and self-assessing your work deepens your understanding of underlying principles and techniques.
Effective Strategies for Self-Assessment
- Review Step-by-Step: Don’t just compare final answers. Go through each step to ensure that the reasoning and procedures align with the solutions provided.
- Analyze Errors: When discrepancies arise, break down where you went wrong–was it in interpreting the question, using the wrong method, or a calculation mistake?
- Seek Alternatives: If you missed a step or approached a problem differently, try to find multiple methods of solving the same problem and understand the benefits of each approach.
- Reflect Regularly: Make self-assessment a part of your routine after each task or set of problems, reinforcing your knowledge and continuously improving your skills.
By using a solution guide for self-assessment, you are actively engaging in the learning process, becoming more mindful of your methods, and developing a deeper understanding of the material. It’s a powerful way to ensure long-term success and mastery in problem-solving.
Ensuring Accuracy in Your Math Solutions
Achieving precision in solving complex problems is a fundamental goal in any learning process. Accuracy in calculations and reasoning ensures that the results are reliable and meaningful. With the right techniques and a careful approach, it’s possible to minimize errors and maximize the understanding of concepts. Whether working through equations, graphing data, or applying formulas, maintaining accuracy is key to mastering problem-solving skills.
One of the most effective ways to ensure accuracy is by double-checking each step of the process. Whether you’re solving a multi-step problem or performing a simple calculation, verifying your work helps to catch potential mistakes before finalizing your answers. The method of self-checking can be especially valuable when you are reviewing solutions or when you feel uncertain about your results.
Key Practices for Accurate Problem Solving
- Break Down the Problem: Start by clearly understanding the problem. Break it down into smaller, manageable steps, ensuring each part is addressed correctly.
- Check Your Calculations: Always revisit your calculations, even if they seem straightforward. It’s easy to overlook small errors in arithmetic.
- Understand the Concepts: A solid understanding of the underlying principles reduces the likelihood of misapplication or incorrect assumptions.
- Use Proper Tools: Make use of calculators or other tools as needed, but always verify that they are used correctly to avoid technical errors.
- Verify Units: Especially in problems involving measurements, always ensure that the units are consistent throughout your solution.
Using Solutions as a Reference
Reviewing correct solutions alongside your own work can also support the accuracy of your problem-solving. Comparing your approach to a well-executed solution helps to identify areas for improvement and prevent repeating common errors. It’s essential, however, to focus not just on the final result but also on the steps that lead up to it. By evaluating the methodology behind a solution, you gain deeper insight into the reasoning that contributes to an accurate outcome.
Furthermore, keeping a consistent practice of checking your work will gradually improve your problem-solving skills and reduce the chances of making mistakes. Accuracy is built over time with consistent effort and attention to detail, reinforcing the confidence needed for more complex tasks.
Integrating Answer Keys into Study Habits
Incorporating solution guides into regular study routines can significantly enhance learning and retention. These resources not only provide a way to check correctness but also serve as a valuable tool for understanding the underlying principles behind each problem. When used strategically, solution references can help identify areas of weakness, guide independent learning, and foster a deeper understanding of the subject matter. It’s important to approach these tools as part of a larger learning strategy, rather than relying on them solely to confirm answers.
To maximize the benefits, it’s essential to integrate these resources into the study process in a way that promotes active learning. Instead of simply referring to solutions after attempting a problem, students should engage with them thoughtfully. By analyzing each step in the solution, learners can identify their mistakes and understand why certain approaches lead to correct results. This process of self-reflection helps build critical thinking skills and reinforces the concepts being studied.
Strategies for Effective Use of Solution Guides
- Use as a Learning Tool: Rather than simply checking answers, use solutions to understand the steps involved. Reflect on how the approach works and why it’s effective.
- Don’t Rush: Avoid immediately looking up solutions. Try to work through problems independently first to develop problem-solving skills.
- Break Down Solutions: When reviewing solutions, break them down into smaller, digestible parts to better understand the reasoning behind each step.
- Make Corrections: If you make mistakes, take the time to correct them and understand what went wrong. This practice helps prevent the same errors in the future.
Building Consistency in Study Habits
Consistency is key when incorporating solution references into study habits. Set aside dedicated time each day to practice, review problems, and evaluate your progress. By consistently applying these strategies, students can turn their study sessions into opportunities for growth, mastering the material over time. With this approach, solution guides become more than just a tool for checking work–they become an integral part of the learning process, helping students to deepen their understanding and achieve greater success.
When to Rely on the Answer Guide
Knowing when to use solution references can be crucial for effective learning. While these resources are helpful, relying on them at the wrong times can hinder the development of problem-solving skills. It’s essential to find a balance between independent problem solving and consulting these tools. This section discusses when it’s appropriate to refer to solutions and how to use them effectively to reinforce learning without becoming overly dependent.
When to Consult the Solution Guide
- After Attempting a Problem: Use the reference to check your approach after you’ve tried to solve the problem on your own. This ensures that you’re not simply copying answers but actively engaging with the material.
- When Stuck on a Specific Step: If you’re stuck on a particular part of the problem and can’t seem to move forward, the guide can help clarify the next logical steps or offer insight into where you went wrong.
- To Check Understanding: After solving a problem, verify that your understanding aligns with the solution presented. If your solution matches but the steps differ, review why the reference method is more effective.
- For Concept Reinforcement: If you’re struggling with a specific concept, revisiting solved examples can provide clarification and reinforce your understanding of the methods used.
How to Avoid Over-Reliance on Solution Guides
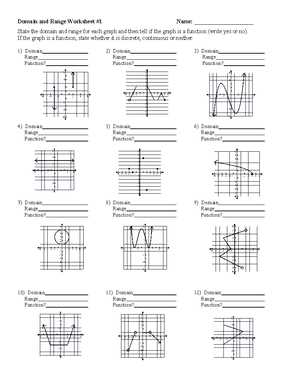
- Limit Usage: Try to solve problems independently for as long as possible before consulting the guide. This helps build critical thinking and reinforces learning.
- Review Mistakes: If you consult a solution guide and find errors in your work, take time to understand why the mistake occurred, and make a note of common pitfalls to avoid in future exercises.
- Seek Help Only When Necessary: Solution guides should be used as a supplementary tool, not a crutch. Turn to them only when you’ve exhausted all other options or when you’ve genuinely learned from your initial attempts.
Improving Performance with Solution Insights
Utilizing solution guides effectively can be a powerful tool for enhancing your understanding and performance. These resources offer valuable insights into correct methods and approaches, helping to identify both strengths and areas for improvement. By examining how solutions are structured and comparing them to your own work, you can refine your techniques and boost your problem-solving abilities. This section explores how to leverage solution insights to enhance your overall performance and accelerate learning.
Maximizing the Benefit of Solution Insights
- Identify Patterns and Techniques: Review multiple examples to recognize patterns in how solutions are solved. Understanding the underlying strategies can help you apply similar methods to different problems.
- Evaluate Your Problem-Solving Approach: Compare your methods with those in the solution guide. If your approach is inefficient or unclear, adjust it to align with more effective strategies.
- Focus on Steps You Missed: When your solution differs from the reference, examine the specific steps you missed. This will help you identify gaps in your knowledge and clarify areas where you need further practice.
- Use Solutions for Reflection: After solving a problem, refer to the solution guide not only to verify your answer but also to reflect on the process. This reflection strengthens retention and deepens understanding.
Tracking Progress and Performance Improvement
- Set Milestones: As you review solutions, track your progress by noting which types of problems you can now solve without needing to consult the guide. This helps build confidence and motivates further learning.
- Address Repeated Mistakes: If certain mistakes occur frequently, focus on those areas in your review. Identifying recurring issues is the first step in eliminating them and improving accuracy.
- Self-Test Regularly: Use solved examples as a benchmark to test your knowledge. Challenge yourself to solve similar problems independently, then check your work against the solution guide to verify progress.