In many fields of study, especially mathematics and science, we often encounter numbers that are either extremely large or incredibly small. These numbers can be difficult to manage or express in their standard form. A more efficient way of handling such figures is through a method that simplifies their representation, making them easier to read, work with, and compare.
This method involves rewriting numbers in a compact form that highlights their magnitude and scale. By breaking down large or small values into a product of simpler components, it becomes much easier to perform calculations or make meaningful comparisons. Whether you’re dealing with measurements in physics, large data sets in statistics, or other complex scenarios, mastering this technique is essential.
Throughout this guide, we will explore how to transform numbers using this approach, focusing on providing clear examples and step-by-step instructions. By the end, you’ll have a solid understanding of how to interpret and manipulate these representations effectively. Whether you’re a student, professional, or simply curious, mastering this concept is a valuable skill that will enhance your problem-solving ability.
Understanding Exponential Number Representation
When working with numbers, it is often necessary to express values that are either extremely large or extremely small in a manageable way. This is where a more efficient form of writing numbers comes into play, allowing us to simplify complex values and make them easier to read and calculate. By condensing these figures into a smaller format, they become more practical for use in various fields like science, engineering, and mathematics.
Rather than writing out long strings of digits, this method breaks numbers into two parts: one representing the base and the other indicating the magnitude of the number. This system enables us to express a wide range of values with minimal effort, enhancing clarity and simplifying calculations. It’s especially useful when dealing with measurements in areas such as physics, where large numbers like the speed of light or tiny quantities like atomic measurements are common.
Mastering this method allows for quicker comparisons, easier calculations, and a deeper understanding of how different values relate to one another. It serves as a fundamental tool for simplifying otherwise cumbersome numbers, providing a clear and concise way to handle both enormous and tiny quantities alike.
What is Exponential Number Representation
In many areas of mathematics and science, we frequently encounter numbers that are either exceedingly large or very small. Representing these values in their full form can become cumbersome and difficult to work with. A more efficient method exists that allows these numbers to be written in a simplified structure, making them easier to interpret and manipulate.
This approach involves expressing numbers as a product of two components: a base and an exponent. The base typically lies between 1 and 10, and the exponent indicates how many places the decimal point must move to express the number in its full form. This system streamlines the representation of vast quantities or minuscule values without losing precision.
Below is an example that illustrates how this method works:
| Full Number | Exponential Form |
|---|---|
| 100,000,000 | 1 × 108 |
| 0.000034 | 3.4 × 10-5 |
By using this system, extremely large and small values become easier to handle and work with, both in theoretical calculations and practical applications. Whether you’re analyzing astronomical distances or microscopic measurements, this technique offers a clear and efficient method for managing numbers across a wide range of magnitudes.
Converting Numbers to Exponential Form
Converting a number to its simplified exponential format involves representing it as a product of a base and an exponent. This method is particularly useful for handling large or small values that would otherwise be difficult to work with. The process helps reduce the number of digits involved while preserving the value’s magnitude and precision.
Steps for Conversion
To convert a number into exponential form, follow these basic steps:
- Identify the decimal point in the number.
- Move the decimal point so that the number is between 1 and 10.
- Count how many places the decimal point was moved. This becomes the exponent.
- If the decimal point moves to the right, the exponent is negative. If it moves to the left, the exponent is positive.
Example of Conversion

Let’s look at an example to better understand the process. Suppose you need to convert the number 450,000,000 into exponential form:
- First, move the decimal point to between 4 and 5: 4.5.
- Next, count how many places the decimal point moved: 8 places to the left.
- The result is 4.5 × 108.
This simplified representation makes it easier to work with large numbers, especially in calculations or scientific contexts where such values are common.
Key Rules for Exponential Representation
When working with large or small numbers in a compact form, there are certain principles that guide how these values should be written. These rules ensure consistency and accuracy, allowing anyone using this method to interpret and perform calculations easily. Understanding these guidelines is crucial to mastering this technique.
General Guidelines
To express a number correctly in exponential form, follow these important rules:
- The base should always be a number between 1 and 10.
- The exponent represents the number of places the decimal point has been moved. If the decimal point moves to the left, the exponent is positive; if it moves to the right, the exponent is negative.
- When converting small numbers (less than 1), the exponent will be negative, reflecting the movement of the decimal point to the right.
- When converting large numbers (greater than 1), the exponent will be positive, reflecting the movement of the decimal point to the left.
Examples of Proper Form
Here are a few examples to illustrate these rules:
- 450,000,000 becomes 4.5 × 108.
- 0.0000034 becomes 3.4 × 10-6.
By adhering to these simple guidelines, you’ll be able to easily convert and work with large and small numbers in an efficient and accurate manner.
Examples of Exponential Number Problems
One of the best ways to understand how to work with large and small values in a compact form is through practice problems. These problems help you apply the rules and techniques for converting and calculating with such numbers. Below are a few examples that illustrate how to handle various types of numbers in exponential form.
Problem 1: Converting Large Numbers
Let’s start by converting a large number into its compact form:
- Given number: 12,000,000,000
- Move the decimal point to between 1 and 10: 1.2
- Count the number of places the decimal moved: 10 places to the left
- Answer: 1.2 × 1010
Problem 2: Converting Small Numbers
Next, let’s convert a small number into its exponential form:
- Given number: 0.000048
- Move the decimal point to between 4 and 5: 4.8
- Count the number of places the decimal moved: 5 places to the right
- Answer: 4.8 × 10-5
Problem 3: Multiplying Exponential Numbers
Now, let’s look at how to multiply two numbers in exponential form:
- Given numbers: 2 × 104 and 3 × 103
- Multiply the base numbers: 2 × 3 = 6
- Add the exponents: 4 + 3 = 7
- Answer: 6 × 107
Problem 4: Dividing Exponential Numbers

Lastly, let’s solve a division problem with numbers in exponential form:
- Given numbers: 6 × 108 and 2 × 103
- Divide the base numbers: 6 ÷ 2 = 3
- Subtract the exponents: 8 – 3 = 5
- Answer: 3 × 105
These examples show how to convert and perform basic operations on numbers in compact exponential form. With practice, these techniques become second nature, making it easier to handle complex values in both theoretical and practical contexts.
How to Simplify Exponential Number Form
Simplifying large or small numbers expressed in compact form involves reducing them to their most basic and manageable expression. This process can make it easier to perform calculations, compare values, and understand the scale of numbers. Simplification typically focuses on adjusting the base and the exponent so that the number is written in the simplest possible way while maintaining its value.
To simplify a number, the main goal is to ensure the base falls within a specific range, typically between 1 and 10. If the base exceeds 10 or is smaller than 1, adjustments must be made to the base while also modifying the exponent accordingly. This method streamlines the number and makes it easier to work with in equations or when making comparisons.
Here are the basic steps to simplify a number in this form:
- Check if the base is between 1 and 10. If it’s not, adjust it accordingly.
- If the base is too large, divide it by 10 and increase the exponent by 1.
- If the base is too small, multiply it by 10 and decrease the exponent by 1.
By following these steps, the number is converted into its simplest form, making it easier to use in various applications, from solving equations to interpreting scientific data.
Exponential Representation and Large Numbers

When dealing with vast quantities, whether in physics, astronomy, or other fields, working with extremely large numbers can become cumbersome. Using a more compact form to express these values allows for easier handling, clearer communication, and more efficient calculations. By expressing these large numbers in a simplified structure, we can avoid writing out lengthy strings of digits while maintaining precision.
For very large numbers, this method involves expressing them as a product of a base and an exponent. The base is typically a number between 1 and 10, while the exponent indicates how many times the base should be multiplied by 10. This allows us to express numbers like the distance between stars or the mass of planets in a much more manageable format.
For example, the number 100,000,000,000 can be written as 1 × 1011. This compact form makes it much easier to work with such vast quantities in both theoretical and practical contexts.
This approach is essential when calculating large distances, like the distance between Earth and other galaxies, or dealing with measurements in fields such as chemistry or astronomy, where numbers can span an enormous range. Using this simplified format helps professionals avoid errors and ensures that values remain manageable and understandable.
Working with Small Numbers in Exponential Form

When dealing with very small quantities, expressing them in a compact format makes it easier to manage and perform calculations. Small numbers, especially those less than 1, are often difficult to handle directly due to their long decimal expansions. By converting these numbers into a simplified form, you can quickly compare them, calculate, and work with them in various scientific and technical fields.
In this approach, the number is expressed as a base between 1 and 10, multiplied by a power of 10. The exponent indicates the magnitude of the number and is negative for small values, reflecting how many places the decimal point is moved to the right.
| Number | Exponential Form |
|---|---|
| 0.000007 | 7 × 10-6 |
| 0.000000032 | 3.2 × 10-8 |
| 0.00015 | 1.5 × 10-4 |
In these examples, the negative exponent shows how the decimal point moves to the right to convert the number into a form between 1 and 10. This format is extremely useful for scientific calculations, where precision and simplicity are essential.
Common Mistakes in Exponential Number Form
When working with numbers in exponential form, it’s easy to make mistakes, especially when converting between standard form and compact representation. These errors can lead to confusion and incorrect results, particularly in complex calculations. Understanding and avoiding the most common mistakes will help ensure accuracy and efficiency when using this method.
1. Incorrect Placement of the Decimal Point
One of the most frequent mistakes is misplacing the decimal point when converting numbers to or from compact form. This can result in either too large or too small of an exponent, leading to incorrect values.
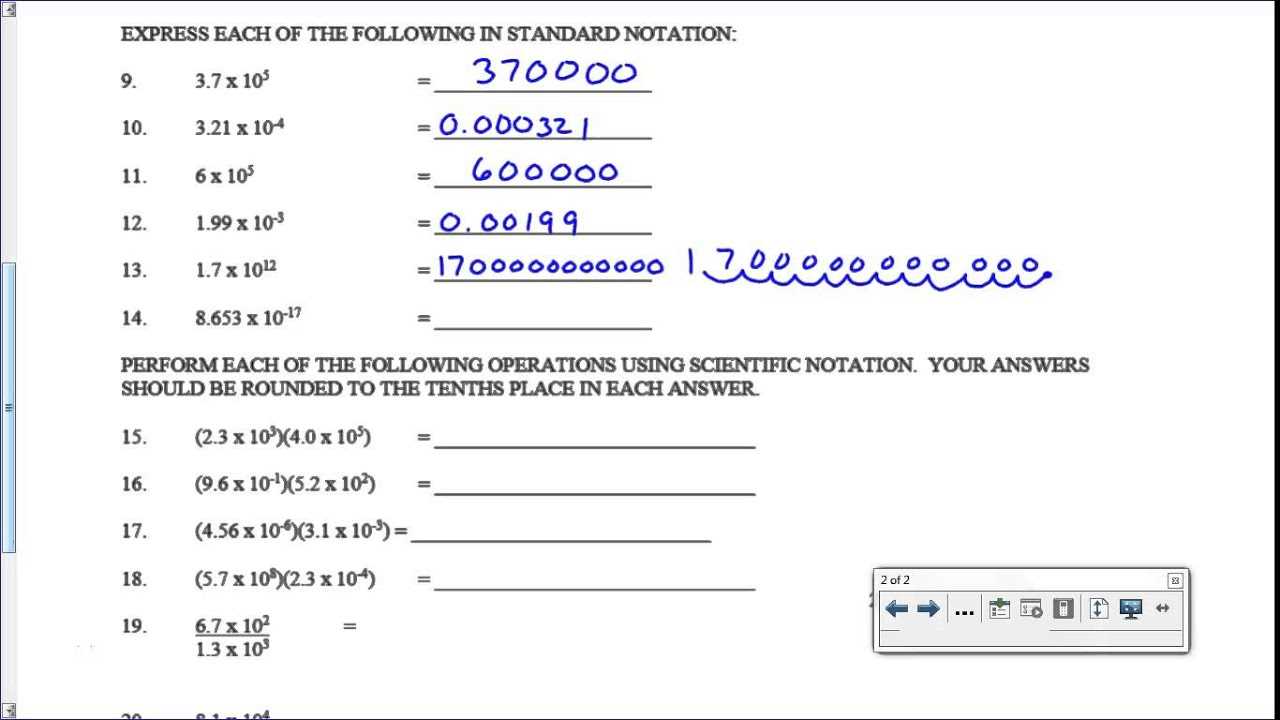
- Example: Converting 0.00045 as 4.5 × 10-4 instead of 4.5 × 10-5.
- How to avoid: Carefully count the number of decimal places moved when converting.
2. Incorrectly Adding or Subtracting Exponents
When multiplying or dividing numbers in exponential form, it’s essential to remember the rules for working with exponents. A common mistake is adding or subtracting the exponents incorrectly during these operations.
- Example: 3 × 104 multiplied by 2 × 105 should result in 6 × 109, not 6 × 1010.
- How to avoid: Double-check the arithmetic for the exponents and ensure you’re applying the correct operation–add for multiplication, subtract for division.
By being mindful of these common errors, you can improve the accuracy and efficiency of your calculations and ensure that you’re working with numbers in their correct form.
Adding and Subtracting in Exponential Form
When working with numbers in exponential form, adding and subtracting values require special attention to the exponents. Unlike multiplication and division, where you combine the exponents directly, addition and subtraction involve making sure the numbers have the same exponent before performing any arithmetic. This step is crucial to ensure that the operations are done correctly and the result is accurate.
Before performing addition or subtraction, it’s essential to adjust the exponents so that they match. Once the exponents are the same, you can simply add or subtract the coefficients (the numbers before the powers of 10). If the exponents are different, you’ll need to convert one of the numbers so that both have the same exponent, which can involve either increasing or decreasing the exponent accordingly.
Here’s how to approach adding and subtracting in exponential form:
- Ensure both numbers have the same exponent.
- If the exponents are different, adjust the numbers by shifting the decimal point.
- Once the exponents match, add or subtract the coefficients as normal.
For example, to add 2 × 103 and 3 × 104, you first adjust 2 × 103 to 0.2 × 104. Then, you can add the coefficients: 0.2 + 3 = 3.2. The result is 3.2 × 104.
Multiplying Numbers in Exponential Form

Multiplying numbers in exponential form is straightforward once you understand the basic principles. The process involves two main steps: multiplying the coefficients and adding the exponents. By following these simple rules, you can efficiently work with very large or small numbers in a compact and manageable way.
First, you multiply the coefficients (the numbers in front of the powers of 10) as you would with any regular numbers. Then, you add the exponents of the powers of 10. This rule applies whether the exponents are positive or negative, making it easy to perform calculations without manually writing out large numbers.
Here’s a step-by-step example:
- Consider multiplying 3 × 104 by 2 × 103.
- First, multiply the coefficients: 3 × 2 = 6.
- Then, add the exponents: 4 + 3 = 7.
- The result is 6 × 107.
This method works for any pair of numbers in exponential form, whether the numbers are extremely large or small. By following these steps, you can simplify complex multiplication problems and perform calculations more easily.
Dividing Numbers in Exponential Form

Dividing numbers in exponential form is similar to multiplying them, with a key difference: instead of adding exponents, you subtract them. This makes division straightforward when working with large or small numbers. The steps for division involve both dividing the coefficients and subtracting the exponents, which can be done quickly using the basic rules of exponents.
Step-by-Step Process
To divide two numbers in exponential form, follow these steps:
- Divide the coefficients (the numbers in front of the powers of 10).
- Subtract the exponent of the divisor from the exponent of the dividend.
For example, dividing 6 × 105 by 2 × 103:
- First, divide the coefficients: 6 ÷ 2 = 3.
- Then, subtract the exponents: 5 – 3 = 2.
- The result is 3 × 102.
Handling Negative Exponents
When the exponents are negative, the same rules apply. The subtraction of exponents still works, and the result will indicate whether the number is very small or large. This allows for seamless division of both small and large values, ensuring consistency in your calculations.
Exponential Form in Real Life
Numbers expressed in exponential form are commonly used in various real-world applications, especially when dealing with values that are either extremely large or small. These types of expressions make it easier to represent, compare, and work with such numbers without writing out long strings of digits. From the fields of science to finance, exponential notation is essential for simplifying complex calculations and making data more manageable.
In many scientific disciplines, including physics and chemistry, values such as the speed of light, atomic sizes, and distances in space are often represented in exponential form. For example, the mass of an electron is a very tiny number, expressed as 9.11 × 10-31 kilograms. Without using this shorthand, such a number would be impractical to write or work with regularly.
Similarly, in astronomy, distances between celestial objects are incredibly vast, making exponential form an invaluable tool for expressing these distances. For example, the distance from Earth to the nearest star, Proxima Centauri, is about 4.24 × 1013 kilometers. Without exponential notation, such numbers would be unwieldy and difficult to understand.
Practical Uses
- Computing scientific data: Exponential expressions simplify complex numbers in scientific research, especially in physics and chemistry.
- Astronomy and space exploration: Large distances and measurements, such as light years and stellar masses, are expressed concisely.
- Technology and computing: Storage capacity, processing power, and internet speeds are often calculated using exponential values.
In finance, exponential notation also plays a key role in representing very large amounts of money or interest rates, such as those used in compound interest calculations or national debt figures. By using this system, calculations become more efficient and easier to understand, even for values that span multiple orders of magnitude.
Using Exponential Form in Calculators
When working with very large or small numbers, calculators often use a special shorthand method to handle these values efficiently. This is especially useful in scientific, engineering, and financial calculations, where precision is required. Most modern calculators can automatically convert numbers into this shortened format, allowing for easier computation and preventing errors in handling complex numbers.
Steps for Entering Exponential Form in a Calculator
To use exponential notation in a calculator, follow these basic steps:
- Enter the coefficient, the number before the exponential part.
- Press the “EXP” or “EE” button, which indicates the exponential part of the number.
- Enter the exponent, which is the power of 10 by which the coefficient is multiplied.
- Press “Enter” or “=” to compute the result.
For example, to enter 3.2 × 105, you would type 3.2, press the “EXP” button, type 5, and then press “Enter.” The display should show the result in exponential form.
Understanding the Display
When using a calculator, the result may appear in a compact format, often showing the exponent with “E” or “EXP” followed by the exponent number. For example, 3.2 × 105 may be displayed as 3.2E5. This is simply another way of representing the same number, and it’s helpful when dealing with very large or very small values that would otherwise take up a lot of space on the screen.
Many scientific calculators are designed to handle these expressions seamlessly, allowing users to input and manipulate numbers without needing to manually convert them into more manageable forms. This functionality saves time and ensures accuracy, especially when performing repetitive calculations in fields like physics, engineering, or computer science.
Applications in Science and Engineering

In various technical fields, particularly in science and engineering, the ability to work with very large and small values is essential. Whether it’s calculating the mass of atoms or the distance between celestial bodies, compactly representing these values makes complex calculations more manageable. This method of expressing numbers allows professionals to work more efficiently and accurately with measurements that span multiple orders of magnitude.
Key Areas of Use
- Astronomy: In astronomy, distances between stars, galaxies, and other celestial bodies are enormous. Using this shorthand method allows scientists to express these distances concisely, facilitating calculations of space travel, energy output, and the scale of the universe.
- Physics: Physics often deals with values like atomic sizes or the speed of light, which are incredibly small or large. The use of exponential expressions helps physicists communicate and compute values that would otherwise be difficult to represent in standard decimal form.
- Engineering: Engineers frequently work with measurements of force, pressure, and material properties that vary greatly. Using this notation ensures precision and consistency when dealing with components that span a wide range of scales, from microchips to massive construction structures.
- Chemistry: In chemistry, particularly when measuring concentrations or molecular sizes, this shorthand method allows chemists to easily work with very small quantities, such as the concentration of ions in a solution or the number of molecules in a sample.
Real-World Examples
- In particle physics, the mass of subatomic particles like electrons or quarks is measured in tiny fractions of a gram, often expressed in exponential form for simplicity.
- When calculating the speed of light, scientists use extremely large numbers, which are more easily managed when written in exponential form (e.g., 3 × 108 meters per second).
- In civil engineering, calculations involving materials like steel or concrete often require large values for density, stress, or load-bearing capacity. Exponential expressions make it easier to compare and manipulate these values.
This method simplifies communication among professionals and aids in reducing errors during complex calculations, making it indispensable across a range of technical disciplines.
Practical Tips for Mastering Notation
Mastering the process of working with values expressed in exponential form can seem challenging at first, but with a few strategies, you can gain confidence and improve your skills. Understanding how to convert, manipulate, and simplify these numbers is a valuable skill in both academic and professional settings. The key lies in practice, clarity, and consistency when applying the rules.
Start with the Basics: Ensure you have a solid understanding of how these values are structured. Begin by learning how to identify the base number and the exponent. This is crucial for correctly interpreting and converting numbers, and it will form the foundation for all other operations.
Practice Conversions: Regularly practice converting numbers from standard form to exponential form and vice versa. The more you practice, the quicker and more accurate you’ll become. Work through examples from simple to complex, gradually increasing the difficulty level.
Understand Exponent Rules: Familiarize yourself with the rules for multiplying, dividing, and adding numbers in exponential form. For example, when multiplying two values, you add the exponents. When dividing, you subtract the exponents. These rules simplify many operations and save time in more complex calculations.
Use Estimation: When dealing with extremely large or small numbers, try estimating the result before performing the full calculation. This will help you get a sense of whether your final result is reasonable, and it can also help you check your work.
Work Through Examples: Solve a variety of problems to reinforce your understanding. Start with straightforward examples, then gradually introduce more challenging scenarios, such as those involving multiple steps or requiring conversion between different forms.
Leverage Technology: Take advantage of calculators or online tools that can help you practice and verify your calculations. Many scientific calculators have built-in features that automatically handle numbers in exponential form, making it easier to check your work.
By consistently practicing these techniques and integrating them into your regular study routine, you can develop fluency in working with numbers in exponential form. Over time, these concepts will become second nature, allowing you to handle even the most complex calculations with ease.
Practice Problems for Scientific Notation
Working through problems is one of the best ways to reinforce your understanding of working with numbers in exponential form. The more problems you solve, the more confident you’ll become in handling these numbers efficiently. Below are several practice exercises designed to help you sharpen your skills. Start with the basic examples and gradually challenge yourself with more complex problems.
Basic Conversion Problems
1. Convert the number 450,000 into exponential form.
2. Convert the number 0.000032 into exponential form.
3. Express 5,200,000 as a number with an exponent.
4. Convert 0.000000745 into exponential notation.
Operations with Exponential Form

1. Multiply the numbers 4 × 103 and 3 × 105.
2. Divide the numbers 6 × 108 by 2 × 104.
3. Add the numbers 3 × 106 and 5 × 107.
4. Subtract 9 × 1012 from 2 × 1013.
For each of these problems, carefully apply the rules of multiplication, division, and addition/subtraction of exponents. By solving them, you will get a clear understanding of how these operations work and how numbers in exponential form can be manipulated. Don’t forget to double-check your results, especially when converting between forms.