In this section, students will encounter important techniques and strategies designed to strengthen their problem-solving abilities. The focus is on mastering essential skills that are foundational for progressing through more complex topics. With a blend of theory and practice, learners will gain a deeper understanding of mathematical structures and operations.
Through carefully structured examples, this guide will help you navigate common challenges while reinforcing core principles. By reviewing different types of problems and their solutions, you will build confidence in your ability to tackle similar tasks on your own. Whether you’re preparing for exams or simply seeking to improve your skills, this section provides a valuable resource for effective learning.
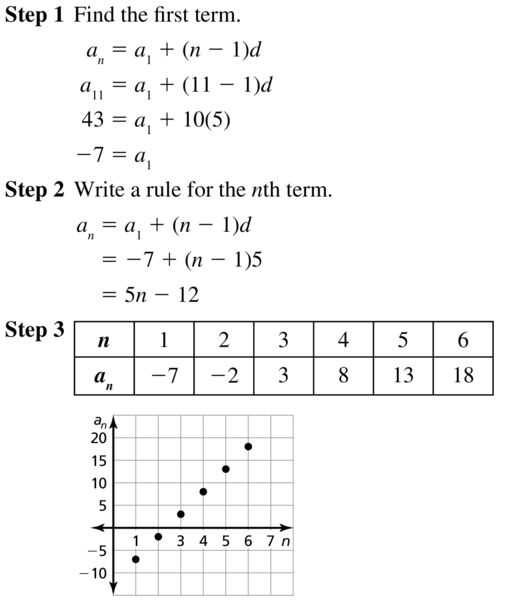
Overview of Chapter 6 Concepts
This section introduces key principles and techniques that form the foundation for solving various types of equations and inequalities. Students will explore a range of methods designed to improve their problem-solving strategies and understanding of relationships between variables. A focus on practical applications ensures that the concepts are not only theoretical but also useful for real-world scenarios.
Within this topic, the following core areas are covered:
- Linear equations and their solutions
- Understanding and working with inequalities
- Graphing solutions to equations
- Solving word problems involving equations
- Identifying key patterns in numerical data
Each of these concepts builds on previously learned material, offering a more advanced approach to handling mathematical problems. Mastery of these ideas will help develop both analytical and critical thinking skills that are essential for tackling more complex tasks later on.
Key Topics Covered in Chapter 6
This section delves into essential topics that are crucial for developing a deeper understanding of mathematical problem-solving. By examining various techniques, students will enhance their ability to work with different types of equations, inequalities, and expressions. Each concept is introduced with clarity and followed by practical examples to reinforce learning.
The primary areas explored in this section include:
- Solving linear equations with one variable
- Working with inequalities and their graphical representations
- Understanding the properties of slopes and intercepts
- Graphing systems of equations and finding solutions
- Solving multi-step equations
- Translating real-world problems into mathematical expressions
These topics are integral to building a solid foundation for future mathematical learning and application. Mastering these concepts will allow students to approach more advanced topics with confidence and clarity.
Understanding Algebraic Equations
Equations serve as a fundamental tool in mathematics, representing relationships between variables. Understanding how to manipulate and solve these expressions is essential for progressing to more advanced topics. The key to solving an equation is recognizing its structure and applying the correct operations to isolate the unknown values.
Basic Structure of an Equation
At its core, an equation consists of two expressions separated by an equal sign. The goal is to determine the value of the variable that makes both sides of the equation equal. By performing operations such as addition, subtraction, multiplication, or division, we can simplify the equation and solve for the unknown variable.
Solving Linear Equations
Linear equations are the most straightforward type, involving terms with variables raised to the first power. Solving these equations typically requires isolating the variable on one side of the equation. Through systematic steps, students can solve for the unknown variable and verify the solution by substituting it back into the original equation.
Step-by-Step Problem Solving Guide
Solving mathematical problems effectively requires a structured approach. By following a series of logical steps, you can break down complex problems into manageable parts. This method not only improves accuracy but also builds confidence in handling various types of exercises.
Here is a general guide to solving problems in a systematic way:
- Understand the Problem: Read the problem carefully and identify the key information. Determine what is being asked and what is known.
- Translate to Mathematical Form: Convert the given information into an equation or expression. This may involve identifying variables and constants.
- Choose the Correct Method: Decide on the most appropriate technique for solving the problem, such as isolating the variable or applying a formula.
- Solve the Equation: Perform the necessary operations step by step to isolate the variable or simplify the expression.
- Check the Solution: Once you have a solution, substitute it back into the original equation or context to verify its correctness.
By consistently following these steps, you will be able to approach problems methodically, ensuring a greater understanding of the material and more accurate results.
Common Mistakes in Algebra 1
When solving equations and working with expressions, it’s easy to make mistakes that can lead to incorrect results. Recognizing these errors and learning how to avoid them is crucial for improving problem-solving skills. Many common mistakes occur due to misunderstanding the process, overlooking details, or rushing through steps. By addressing these issues, students can develop a clearer approach to solving mathematical problems.
Misunderstanding Order of Operations
One of the most frequent mistakes is not following the correct order of operations. It’s essential to remember that multiplication and division should be performed before addition and subtraction, unless parentheses dictate otherwise. Skipping this step can easily lead to incorrect answers.
Incorrectly Handling Negative Numbers
Another common mistake is mishandling negative signs, especially when adding or subtracting them. It’s important to be cautious when working with negative numbers in equations to avoid sign errors that can change the outcome of the solution.
Tips for Mastering Chapter 6
To excel in this section, it’s important to adopt effective study strategies and maintain a consistent practice routine. Mastery comes from both understanding the concepts and applying them through exercises. By focusing on key techniques and approaching problems methodically, you can improve both your speed and accuracy in solving mathematical tasks.
Practice Regularly and Consistently
Consistency is key when learning new concepts. Set aside time each day to work on problems related to the topics covered. The more you practice, the more comfortable you’ll become with different types of equations and expressions. Start with simple problems and gradually progress to more complex ones as your understanding deepens.
Seek Help When Stuck
Don’t hesitate to ask for assistance when you encounter difficulties. Whether it’s a teacher, tutor, or online resource, seeking clarification can prevent misunderstandings and help you stay on track. Sometimes a fresh perspective can make a challenging concept easier to grasp.
Essential Formulas for Algebra 1
In this section, you’ll encounter key equations that are crucial for solving various types of problems. Understanding and memorizing these formulas will streamline your problem-solving process and ensure you’re prepared for more complex tasks. These formulas provide a framework for tackling equations, simplifying expressions, and working with different mathematical structures.
The following table lists some of the most important formulas you’ll need to master:
| Formula | Description |
|---|---|
| Slope Formula: m = (y2 – y1) / (x2 – x1) | Used to calculate the slope between two points on a graph. |
| Point-Slope Form: y – y1 = m(x – x1) | Equation of a line with slope m passing through point (x1, y1). |
| Standard Form: Ax + By = C | Represents a linear equation, where A, B, and C are constants. |
| Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a | Solves quadratic equations of the form ax² + bx + c = 0. |
| Distributive Property: a(b + c) = ab + ac | Used to expand expressions by distributing the factor over terms in parentheses. |
Familiarity with these formulas is essential for working through the problems in this section and developing a strong foundation for future topics. Regular practice will help you apply them effectively in different contexts.
Solving Word Problems in Algebra

Word problems are an essential part of understanding how to apply mathematical concepts to real-world situations. These problems require you to translate verbal descriptions into equations or expressions that can be solved. The key to success is breaking down the problem into manageable steps and carefully identifying the known and unknown quantities.
To approach word problems effectively, follow these general steps:
- Read the problem carefully: Understand what is being asked and identify the relevant information.
- Assign variables: Represent the unknown quantities with variables, such as x or y.
- Translate to an equation: Convert the written description into a mathematical equation or inequality.
- Solve the equation: Use the appropriate methods to isolate the variable and find its value.
- Interpret the solution: Ensure the solution makes sense in the context of the problem and answer the question.
The table below demonstrates how to approach a typical word problem:
| Problem | Steps | Solution |
|---|---|---|
| A store sells pens for $2 each and notebooks for $3 each. If a customer buys 4 pens and 5 notebooks, how much will they spend in total? |
|
Total cost = $23. |
By practicing these steps regularly, you can develop a more intuitive approach to solving word problems and apply mathematical reasoning to a wide variety of real-world situations.
Practice Exercises for Chapter 6
To reinforce your understanding and improve your problem-solving skills, practicing a variety of exercises is essential. These exercises will help solidify the concepts you’ve learned and allow you to apply them in different contexts. Consistent practice not only boosts confidence but also enhances your ability to tackle more complex problems with ease.
Here are some practice problems that will challenge your knowledge and help you sharpen your skills:
- 1. Solve the equation: 3x + 7 = 22.
- 2. Simplify the expression: 4(2x – 5) + 3x.
- 3. Find the slope of the line passing through the points (2, 5) and (4, 9).
- 4. Solve for y: 5y – 10 = 20.
- 5. Expand and simplify: (x + 3)(x – 4).
- 6. Solve the quadratic equation: x² – 5x + 6 = 0.
- 7. If 2x + 5 = 17, what is the value of x?
- 8. Solve the system of equations: 2x + y = 10 and x – y = 2.
Make sure to follow the problem-solving steps and review your solutions to identify any areas that may need further attention. The more you practice, the more efficient you will become at recognizing patterns and solving equations quickly and accurately.
Explaining Algebraic Expressions
Algebraic expressions are fundamental components of mathematical language, used to represent relationships between variables, constants, and operations. These expressions can describe a wide variety of mathematical scenarios, from simple calculations to complex functions. Understanding how to interpret and manipulate algebraic expressions is essential for solving equations and understanding higher-level concepts.
What is an Algebraic Expression?
An algebraic expression consists of variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. For example, the expression 3x + 5 represents the sum of three times a variable x and the constant 5. The variable x can take on different values, making the expression dynamic and useful for modeling various situations.
Components of Algebraic Expressions
There are several key components that make up an algebraic expression:
- Variables: Symbols that represent unknown values or quantities, such as x, y, or z.
- Constants: Fixed numerical values that do not change, such as the number 5 in the expression 3x + 5.
- Operators: Mathematical operations that relate the terms, such as addition (+), subtraction (-), multiplication (×), or division (÷).
- Coefficients: The numerical factors that multiply the variables, such as the 3 in 3x.
Mastering algebraic expressions is crucial for solving equations, modeling real-world situations, and understanding more advanced topics. By practicing with different expressions, you can develop a deeper understanding of how mathematical relationships work and how to manipulate them to find solutions.
How to Check Your Work
Ensuring the accuracy of your calculations and problem-solving steps is a crucial skill. Verifying your results helps identify mistakes early, saving time and preventing incorrect conclusions. Here are several methods to check your work effectively and ensure the solution is correct.
Step-by-Step Review
One of the best ways to check your work is by reviewing each step of your solution carefully. This allows you to catch any small mistakes you might have overlooked. Follow these guidelines:
- Start from the beginning and read through each step of your solution.
- Double-check your operations (addition, subtraction, multiplication, division) to make sure they are correct.
- Verify the values you substituted into equations or expressions.
- Check that the logic flows properly from one step to the next.
Using a Different Method
Another useful technique is to solve the problem using an alternative method. If the problem allows for different approaches, use one method to solve it, and then solve it again using a different approach. Compare the results to ensure they match.
- If you solved an equation algebraically, try plugging the solution back into the original problem.
- For word problems, check if the solution makes sense in the context of the scenario described.
- Use estimation to see if the result is reasonable.
By using these strategies, you can minimize errors and gain greater confidence in your work. Checking your answers systematically ensures accuracy and builds a deeper understanding of the material.
Real-Life Applications of Algebra
The concepts learned in mathematics are not just abstract ideas; they have practical uses in everyday life. From budgeting finances to understanding trends in science and technology, the principles of solving equations and working with variables play a significant role in problem-solving across various fields. Whether you are designing a project, managing resources, or planning for future outcomes, the skills you develop from understanding mathematical relationships are indispensable.
In the world of business, for example, companies rely on equations to determine pricing strategies, calculate profit margins, and analyze market trends. Engineers use these skills to design structures, optimize processes, and ensure safety standards. In the medical field, algebra helps with dosage calculations, data analysis, and predicting outcomes. These applications demonstrate how essential this knowledge is for making informed decisions and solving complex problems in different areas of life.
By recognizing the importance of these concepts and their impact, you can appreciate how much value they bring to solving real-world challenges. Understanding the connections between abstract mathematical ideas and tangible, real-world situations helps build critical thinking and practical decision-making skills.
Frequently Asked Questions About Algebra
Many students and individuals encounter questions when dealing with mathematical expressions and problem-solving techniques. Whether you’re just starting or revisiting the subject, it’s normal to have doubts and seek clarification. Here, we address some of the most common questions related to solving equations, understanding variables, and applying these concepts effectively.
Common Questions on Solving Equations
- What are variables and how do they work?
Variables are symbols used to represent unknown values. They can stand for numbers or quantities that we need to find when solving problems. - How do I know when to use addition or subtraction in an equation?
You should use addition or subtraction depending on the operation needed to isolate the variable. If the variable has a negative or positive value on one side, you use the opposite operation to cancel it out. - How do I solve equations with fractions?
To solve equations with fractions, find a common denominator or multiply both sides of the equation by the denominator to eliminate fractions.
Common Questions on Understanding Expressions
- What is the difference between an expression and an equation?
An expression represents a combination of numbers, variables, and operators but does not have an equal sign. An equation, however, shows the relationship between two expressions using an equal sign. - Why are parentheses important in expressions?
Parentheses indicate which operations should be performed first. They help structure the order of operations and ensure the correct outcome. - How do I simplify complex expressions?
To simplify expressions, combine like terms and apply the distributive property to make the expression easier to solve or understand.
These questions represent just a few of the common issues people face when working with mathematical expressions and equations. By addressing these concerns, you can build a stronger foundation and gain greater confidence in solving problems effectively.
Reviewing Key Algebraic Principles
When solving equations and manipulating expressions, it’s important to recall the fundamental concepts that form the foundation of problem-solving. These principles help in simplifying calculations, structuring equations correctly, and ensuring accuracy throughout the process. A solid grasp of these concepts is crucial for efficiently tackling various mathematical tasks.
1. The Distributive Property
The distributive property is a critical tool for simplifying expressions. It allows you to multiply a term outside the parentheses by each term inside the parentheses. This principle helps to break down complex expressions into simpler components. For example, a(b + c) = ab + ac.
2. Combining Like Terms
Combining like terms involves adding or subtracting terms that have the same variable and exponent. This step simplifies an expression and is essential for solving equations. For instance, 3x + 5x = 8x.
3. Solving Linear Equations
Solving linear equations requires isolating the variable on one side of the equation. This can be done through operations like addition, subtraction, multiplication, and division. The goal is to determine the value of the unknown that satisfies the equation. For example, in the equation 2x + 3 = 7, subtract 3 from both sides to get 2x = 4, then divide by 2 to solve for x = 2.
4. The Order of Operations
The order of operations is a vital principle to follow when evaluating expressions. It dictates the sequence in which different operations are performed to ensure accuracy. The acronym PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) is often used to remember the correct order.
By understanding and applying these key principles, you can approach problems with greater confidence and avoid common mistakes. Mastery of these concepts is essential for progressing in mathematics and solving more complex problems efficiently.
Preparing for Chapter 7 Transition
As you move forward in your studies, it’s important to prepare for the upcoming material that will build upon what you have learned. The concepts introduced in the next section require a deeper understanding of previous skills, and mastering them will ensure a smooth transition into more complex topics. Review and practice of key principles will be essential to maintaining momentum as you progress.
Master Core Skills
Before advancing, ensure that you are comfortable with the fundamentals covered in earlier lessons. A strong grasp of essential operations such as solving equations, working with expressions, and simplifying terms is vital for tackling the next set of challenges. Strengthen your ability to identify and manipulate variables, constants, and coefficients within different problem types.
Focus on New Concepts
The upcoming topics will introduce new types of equations, advanced operations, and concepts that will require you to apply what you’ve already learned in more complex scenarios. Start familiarizing yourself with these concepts early, and focus on how these new tools build upon your existing knowledge base. This will help you feel more confident as the new material is introduced.
Practice consistently by working on practice problems that reflect the complexity of the upcoming topics. This proactive approach will ensure that you are ready for the transition and will set you up for success in the next stage of learning.
Study Resources for Chapter 6
Access to the right resources can make a significant difference when mastering the concepts presented in this section. Utilizing a variety of study materials will help reinforce your understanding and ensure that you are prepared for assessments. Whether you’re looking for practice exercises, video tutorials, or interactive tools, there are many options available to enhance your learning experience.
Practice Worksheets: Regularly solving problems from worksheets is an effective way to solidify your grasp on key topics. Many resources offer worksheets tailored to the specific concepts covered, allowing you to focus on the areas that need the most attention.
Online Tutorials: Video tutorials are a great way to visualize complex concepts. Many educational websites and platforms offer step-by-step explanations of the material. Watching these can help you understand how to approach and solve different types of problems.
Interactive Tools: Interactive platforms that offer quizzes and challenges can provide immediate feedback, helping you identify areas for improvement. These tools often include explanations of the correct answers, allowing you to learn from your mistakes.
Textbooks and Solution Guides: Comprehensive textbooks and solution guides often contain additional examples, practice problems, and solutions that explain each step in detail. Refer to these guides to reinforce your learning and ensure you understand the reasoning behind each solution.
By leveraging these various resources, you can gain a more thorough understanding and be well-equipped for upcoming assessments and more complex topics in the future.
Improving Algebra Skills Efficiently
Enhancing your problem-solving abilities and mastering key concepts requires focused practice and effective strategies. By approaching each topic methodically and dedicating time to targeted exercises, you can improve your skills in an efficient and structured way. Here are a few strategies to consider for optimizing your learning process.
Effective Study Techniques
- Active Practice: Engage in solving problems regularly. Repetition is key to reinforcing concepts and improving your speed in solving equations.
- Break Down Complex Problems: When faced with more challenging problems, break them down into smaller, manageable steps. This will help you stay focused and reduce the likelihood of mistakes.
- Focus on Conceptual Understanding: Rather than memorizing formulas, aim to understand the reasoning behind each step in a problem. This deeper comprehension will enable you to apply concepts to a variety of situations.
Time Management Strategies
- Set Specific Goals: Establish clear, achievable goals for each study session. Whether it’s mastering a particular technique or solving a set number of problems, clear objectives help track progress.
- Use Timed Practice: Practice solving problems under timed conditions. This will improve your ability to work efficiently under pressure and help you manage time during exams.
- Review Mistakes: Take the time to review errors after completing practice problems. Understanding where you went wrong is a critical step in preventing similar mistakes in the future.
By using these strategies and maintaining a consistent study routine, you will be able to strengthen your skills and tackle more advanced topics with greater confidence.