
In this section, we dive deep into fundamental concepts that serve as the building blocks for more advanced problem-solving techniques. From equations to practical applications, this portion is designed to help learners grasp essential skills and strengthen their understanding of core mathematical principles.
Throughout this guide, we focus on breaking down complex problems into manageable steps. By analyzing key processes and providing clear instructions, we aim to make challenging topics more accessible and easier to approach. The goal is to ensure that each solution is not only correct but also thoroughly understood.
Whether you’re working through exercises or preparing for assessments, this section offers valuable insights and step-by-step approaches to mastering the material. We emphasize clarity and practical strategies to boost confidence and proficiency.
Mathematical Solutions for Section 7

This section focuses on providing detailed solutions to a variety of mathematical problems. The goal is to simplify complex operations and ensure that each step is clearly explained. By reviewing key methods and techniques, learners can strengthen their skills and develop a deeper understanding of the material presented.
Understanding the Key Steps
Each solution is broken down into digestible parts, making it easier to follow the logical flow of problem-solving. Whether solving equations or working with expressions, we aim to make the process as straightforward as possible while maintaining accuracy and clarity.
Step-by-Step Breakdown
Below are some examples of how to approach and solve common problems found in this section. By following the sequence of steps outlined, learners can gain confidence in tackling similar challenges.
| Problem | Step 1 | Step 2 | Solution |
|---|---|---|---|
| Example 1 | Isolate variable | Apply operations | Result: x = 5 |
| Example 2 | Simplify expression | Factor terms | Result: y = 3 |
| Example 3 | Identify coefficients | Solve for unknown | Result: z = -2 |
Overview of Algebra 1 Section 7
This section introduces important concepts and problem-solving techniques that are foundational to mastering more advanced topics. The focus is on strengthening key skills and understanding the relationships between various mathematical elements. By the end of this section, learners should have a solid grasp of essential strategies to solve a range of equations and expressions.
Key Concepts Covered
In this portion, we explore how to manipulate variables, solve linear equations, and work with functions. Emphasis is placed on developing the ability to approach each problem step by step, ensuring clarity in the process. By reviewing examples and practicing exercises, students can build a strong base for tackling complex problems later on.
Learning Objectives

The goal of this section is to ensure that students become comfortable with solving both simple and more challenging problems. By learning how to approach each equation methodically, learners will be able to apply these techniques to a wide variety of scenarios, both in academic settings and real-life applications.
Key Concepts in Section 7
This section explores fundamental ideas that form the backbone of solving a variety of mathematical problems. The focus is on understanding the methods and techniques that allow for simplifying complex equations and expressions. Grasping these core principles is essential for advancing to more intricate topics and building a deeper mathematical intuition.
Solving Linear Equations
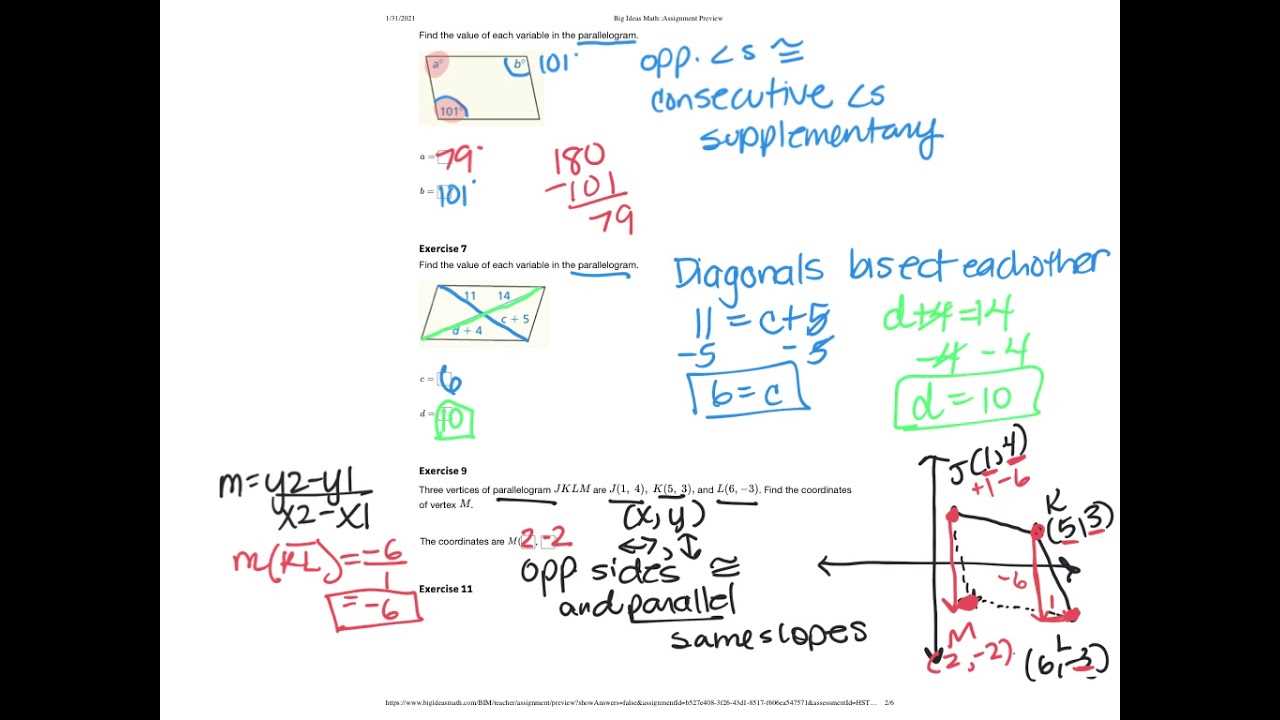
A key component of this section is learning how to solve linear equations. By isolating variables and applying basic operations, students can determine the values that satisfy the equation. Understanding the structure of equations and the properties of equality is crucial for successfully solving these problems.
Working with Functions
Functions are introduced and examined as an essential concept in this section. Learners will explore how to interpret and manipulate functions, gaining the skills needed to work with different types of expressions. By mastering functions, students can easily approach more advanced mathematical challenges.
Step-by-Step Solutions for Each Problem
This section provides a detailed breakdown of how to approach and solve various problems. By following each step, students can understand the logical sequence required to reach the correct solution. The aim is to build confidence by showing how each operation leads to the final answer, making complex problems more manageable.
Breaking Down the Process
Each problem is dissected into clear, easy-to-follow steps. Starting with the initial equation, we will identify the necessary operations and simplify the problem incrementally. This method ensures that learners can follow along without confusion, reinforcing key concepts as they go.
Applying Techniques to New Problems
Once the steps for solving a particular problem are understood, these same techniques can be applied to similar problems. The key is practicing these steps repeatedly to build familiarity with the methods. By working through multiple examples, students can gain proficiency in handling a variety of mathematical challenges.
Common Mistakes to Avoid in Section 7

Understanding common pitfalls is crucial for mastering the material presented in this section. By being aware of frequent errors, students can avoid confusion and strengthen their problem-solving skills. This section highlights some of the most common mistakes and offers tips on how to prevent them while working through exercises.
Incorrect Application of Operations
One of the most frequent mistakes is misapplying basic operations. It’s important to carefully follow the order of operations and apply each step logically. Here are some typical errors:
- Forgetting to distribute terms correctly when dealing with parentheses.
- Mixing up addition and subtraction when solving equations with negative numbers.
- Ignoring the sign of a variable when simplifying expressions.
Misinterpreting Word Problems
Another common issue arises when students fail to fully understand word problems. Misinterpreting the question or overlooking key information can lead to incorrect solutions. To avoid this, always:
- Carefully read the problem and underline important details.
- Translate the words into mathematical expressions step by step.
- Check if the solution makes sense in the context of the problem.
Strategies for Solving Algebraic Equations
Effective problem-solving begins with understanding the best strategies to apply when working with equations. By using the right approach, students can simplify complex problems and find solutions more efficiently. This section outlines several methods that can be used to solve equations, helping to build both accuracy and confidence.
Key Techniques for Solving Equations
There are several strategies that are useful when solving algebraic equations. By mastering these methods, students can approach any problem with a clear plan:
- Isolating the variable: Move all terms involving the unknown to one side of the equation and constants to the other side.
- Balancing the equation: Ensure that every operation performed on one side is also applied to the other side to maintain equality.
- Simplifying expressions: Combine like terms and simplify complex expressions before solving for the unknown.
- Checking solutions: After finding a solution, substitute it back into the original equation to verify its correctness.
Using Graphical Methods
Another helpful technique is solving equations using graphical methods. Plotting the equation on a graph can provide visual insights into the solution, especially when working with linear equations. Follow these steps:
- Rewrite the equation in slope-intercept form (y = mx + b) if necessary.
- Plot the equation on a coordinate plane.
- Identify the point of intersection with the x-axis or y-axis to find the solution.
Understanding Functions in Section 7
Functions play a central role in this section as they are essential tools for describing relationships between variables. Understanding how to interpret and manipulate functions is key to progressing through more advanced mathematical concepts. By mastering the fundamentals of functions, students can confidently apply them to a variety of problems.
What is a Function?
A function is a relationship between two sets where each input has exactly one output. In this section, the focus is on identifying functions, analyzing their properties, and learning how to represent them in different forms. Whether expressed algebraically, graphically, or in tables, understanding functions is fundamental for solving problems and making predictions based on given data.
Graphing and Analyzing Functions
Graphing is one of the most effective ways to visualize a function. By plotting points and analyzing the shape of the graph, you can better understand how the function behaves. Functions can be linear, quadratic, or more complex, and each type has its own distinctive graph:
- Linear functions: These are represented by straight lines and are characterized by a constant rate of change.
- Quadratic functions: These are represented by parabolas and exhibit a varying rate of change.
By learning to graph and interpret these functions, students can gain insights into their properties and behavior, helping them solve related equations and apply them to real-world scenarios.
Solving Linear Equations in Detail

Solving linear equations is a fundamental skill in mathematics, as it forms the basis for more complex problem-solving methods. This section focuses on providing a clear, step-by-step approach to solving equations that involve variables raised to the first power. The goal is to understand the process of isolating the variable and applying operations that maintain the balance of the equation.
To solve a linear equation, the main objective is to find the value of the variable that makes both sides of the equation equal. This is done by performing inverse operations on both sides, such as addition, subtraction, multiplication, and division. Each step should be carefully executed to avoid common mistakes that can lead to incorrect results.
Once you have isolated the variable, it is important to check your solution by substituting it back into the original equation. If both sides of the equation are equal, you have successfully solved the problem. This verification step is crucial for ensuring accuracy and reinforcing the correct method.
Word Problems and Solutions Explained
Word problems can often be intimidating, but with the right approach, they become manageable. These problems require translating a real-world situation into a mathematical equation, and then solving it. The key is to break down the problem into smaller, more understandable steps, and to carefully interpret the information given.
Steps for Solving Word Problems
When tackling word problems, it’s helpful to follow a structured process:
- Read the problem carefully: Make sure to understand what is being asked and identify the key information provided.
- Translate words into equations: Convert the given information into a mathematical expression that you can solve.
- Solve the equation: Use appropriate methods, such as simplifying or isolating the variable, to find the solution.
- Interpret the solution: Once the equation is solved, review the result in the context of the problem to ensure it makes sense.
Example Problem and Solution
Here’s an example of how to solve a word problem:
- Problem: A store sells apples at $3 each. If a customer buys a certain number of apples and pays $15, how many apples did they buy?
- Solution: Let the number of apples be represented by x. The equation to solve is: 3x = 15. Divide both sides by 3 to get x = 5.
- Interpretation: The customer bought 5 apples.
By following these steps, students can effectively approach and solve word problems with confidence.
Tips for Mastering Section 7 Skills
Mastering the skills taught in this section requires consistent practice, focus, and a clear understanding of the core concepts. Whether you are working through equations, functions, or word problems, there are strategies you can use to improve your proficiency and build confidence. By focusing on key areas and employing effective study habits, you can ensure success in this section.
One of the most important tips is to break down each concept into manageable steps. Avoid rushing through problems–take the time to understand each process thoroughly. Don’t hesitate to review foundational skills if you find yourself struggling with more complex tasks. Additionally, practice solving problems in a variety of formats to strengthen your overall understanding.
Finally, make sure to review your work carefully. Double-check solutions to ensure no steps are skipped, and verify that your final answer makes sense in the context of the problem. Building these habits will help you solidify your knowledge and succeed in mastering the material.
Practice Exercises and Their Solutions
Engaging with practice exercises is essential for reinforcing the concepts learned in this section. By regularly solving problems, you can strengthen your problem-solving skills and build confidence. This section provides various exercises that allow you to apply the techniques discussed and check your understanding of the material.
Exercise 1
Problem: Solve for x in the equation 5x – 3 = 12.
- Solution: Add 3 to both sides: 5x = 15. Then, divide both sides by 5: x = 3.
Exercise 2
Problem: Solve for y in the equation 2y + 6 = 18.
- Solution: Subtract 6 from both sides: 2y = 12. Then, divide both sides by 2: y = 6.
By regularly practicing these types of exercises, you will improve your skills and gain a deeper understanding of the key concepts. Make sure to check your solutions carefully and review any mistakes to enhance your learning.
How to Prepare for Section 7 Tests

Effective preparation for a test requires understanding the key concepts and practicing various types of problems. When approaching a test for this section, it is essential to focus on the skills and techniques that have been covered. Rather than cramming at the last minute, aim to review the material consistently, identify areas where you need improvement, and work through practice problems to reinforce your knowledge.
Start by reviewing the core concepts and ensure that you understand how to apply them in different scenarios. Use practice exercises and sample problems to test your understanding and identify any areas of weakness. Additionally, review any notes or resources provided by your instructor to reinforce what you’ve learned in class.
Make a study plan that allows you to pace yourself, ensuring that you have enough time to cover all topics and revisit difficult concepts. You can also work with a study group to discuss challenging topics and gain a deeper understanding through collaboration.
Preparation Checklist
| Task | Status |
|---|---|
| Review key concepts and formulas | ✔️ |
| Complete practice exercises | ✔️ |
| Focus on problem areas | ❌ |
| Study with a group | ✔️ |
| Take timed practice tests | ❌ |
By following these steps and maintaining a consistent study routine, you will be better equipped to handle the test with confidence and achieve a strong result.
Using Graphs to Solve Algebraic Problems

Graphs are a powerful tool for visualizing and solving equations. By plotting relationships on a coordinate plane, you can easily identify solutions and interpret the behavior of equations. Whether you are solving linear equations or exploring more complex functions, graphs provide a clear and intuitive way to approach problems.
When solving algebraic problems, graphs allow you to find the point where two equations intersect, which represents the solution to the system of equations. This method can also help in understanding the slope, intercepts, and other key characteristics of a function or equation. Additionally, graphs provide a visual representation of how changes in variables affect the outcome, making it easier to analyze and solve problems.
To use graphs effectively, it is important to first understand how to plot points accurately and interpret the meaning of the graph in the context of the problem. Practice graphing different types of functions and equations to strengthen your understanding and improve your problem-solving skills.
Exploring Algebraic Expressions
Algebraic expressions are combinations of numbers, variables, and operations that represent relationships or formulas. They serve as a foundation for understanding mathematical models and solving real-world problems. By manipulating these expressions, you can solve equations, simplify expressions, and model various situations accurately.
In this section, we will explore how to identify and work with different types of expressions, from simple monomials to more complex polynomials. Understanding how to simplify, factor, and expand these expressions is essential for solving a wide range of problems. Moreover, mastering algebraic expressions helps develop critical thinking and problem-solving skills, which are invaluable in both academic and practical contexts.
Simplification of Expressions
Simplifying algebraic expressions involves combining like terms and performing basic arithmetic operations. The goal is to make an expression as concise and manageable as possible, which is crucial for solving equations or modeling real-world scenarios effectively.
Factoring Algebraic Expressions
Factoring allows you to break down complex expressions into simpler components. This process is essential for solving equations, finding roots, and analyzing functions. Learning how to factor different forms of expressions will provide you with a powerful tool for solving a wide range of problems.
Review of Key Formulas and Theorems
Understanding essential formulas and theorems is crucial for solving problems efficiently. These mathematical tools help simplify complex tasks and provide a structured way to approach equations and functions. In this section, we will review some of the most important formulas and theorems that are foundational to solving problems in this subject area.
By becoming familiar with these key formulas, you will be better equipped to tackle various types of equations and problems. Each formula has a specific purpose and can be applied in different scenarios, making it important to understand when and how to use them.
Important Formulas to Remember

| Formula | Use |
|---|---|
| Distributive Property: a(b + c) = ab + ac | This property allows you to distribute a number across terms inside parentheses. |
| Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a | Used to solve quadratic equations in the form ax² + bx + c = 0. |
| Slope Formula: m = (y₂ – y₁) / (x₂ – x₁) | Used to calculate the slope between two points on a coordinate plane. |
Key Theorems to Understand
Along with formulas, several key theorems play a vital role in problem-solving. These theorems provide deeper insights into the properties and relationships of mathematical functions.
| Theorem | Explanation |
|---|---|
| Pythagorean Theorem: a² + b² = c² | This theorem is used to calculate the lengths of sides in a right-angled triangle. |
| Zero Product Property: If ab = 0, then a = 0 or b = 0 | Used to solve equations where the product of two expressions is equal to zero. |
Working with Systems of Equations
Systems of equations involve solving multiple equations at once, where the solution is a set of values that satisfy all the equations simultaneously. Understanding how to work with these systems is an essential skill, as they are commonly encountered in various fields, from engineering to economics. This section will guide you through methods to solve systems and provide strategies for different approaches.
There are several techniques to solve systems of equations, each suited for different types of problems. These methods include substitution, elimination, and graphing. Selecting the right method depends on the complexity of the system and the context of the problem.
Methods for Solving Systems of Equations
- Substitution Method: This method involves solving one equation for one variable and then substituting that expression into the other equation. It is especially useful when one equation is easily solvable for a single variable.
- Elimination Method: In this approach, you manipulate the equations to eliminate one variable by adding or subtracting the equations. This method is effective when both equations are aligned in such a way that one variable can be eliminated easily.
- Graphing Method: By graphing both equations on a coordinate plane, the solution to the system is where the two lines intersect. This method gives a visual representation of the solution and is useful when dealing with linear systems.
Example of Solving a System
Let’s look at an example of a system of equations:
x + y = 10 2x - y = 5
- First, we can use the substitution method by solving one equation for one variable (e.g., solve x + y = 10 for y).
- Then, substitute this value for y in the second equation (2x – y = 5).
- After solving for x, substitute that value back into the first equation to solve for y.
By using these steps, you will find the values for both variables that satisfy the system of equations. Practice with different systems will help solidify your understanding of these solving methods.
Applying Chapter 7 in Real-Life Situations
The concepts explored in this section have a wide range of practical applications. Understanding how to work with equations, functions, and systems can be invaluable in solving everyday problems. From budgeting finances to planning construction projects, the principles learned here are used to model and solve problems that arise in the real world. This section will show how these mathematical concepts are applied outside the classroom.
Real-life problems often require you to make decisions based on multiple variables. Whether you’re managing personal expenses, analyzing data trends, or calculating travel times, the techniques covered can provide solutions. By applying equations to practical scenarios, you can better understand and solve complex challenges efficiently.
Practical Applications of Equations

- Budgeting and Financial Planning: Linear equations are frequently used to track income and expenses. For example, setting up a monthly budget can involve creating equations that balance income and expenditure.
- Construction and Design: Engineers and architects use systems of equations to design buildings and structures. By solving equations, they can determine dimensions, calculate areas, and even plan layouts that meet specific criteria.
- Travel and Logistics: Equations are essential when planning travel times or optimizing routes. For instance, if you’re calculating how long it will take to travel between two locations at different speeds, systems of equations can be applied to find the most efficient route or schedule.
Example: Budgeting for a Trip
Imagine you are planning a trip and need to figure out how much money you will spend on travel and accommodation. Using linear equations, you can set up a formula to calculate the total cost, considering factors like travel expenses, hotel rates, and daily expenses. By solving the equation, you can plan accordingly and make sure you stay within your budget.
In this way, the principles learned in this section can help you tackle a variety of situations, allowing you to apply mathematical thinking to everyday challenges. The ability to solve equations and understand their implications is a useful skill for many real-life scenarios.
Additional Resources for Algebra 1
To deepen your understanding and mastery of the concepts discussed, there are various resources available that can provide further practice and explanations. These materials can help reinforce the skills learned and offer alternative approaches to solving problems. Whether you’re looking for online tools, textbooks, or video tutorials, there are plenty of options to explore beyond the classroom.
Online Platforms
- Khan Academy: A widely-used platform that offers comprehensive lessons, practice exercises, and quizzes for various mathematical topics. The interactive nature of the site allows you to learn at your own pace.
- IXL: IXL provides personalized practice questions for various topics, offering immediate feedback to help you improve and master each skill.
- Wolfram Alpha: Known for its powerful computational engine, Wolfram Alpha can solve equations and show step-by-step solutions, helping you better understand how to approach different types of problems.
Textbooks and Study Guides
- Precalculus: Mathematics for Calculus (Stewart, Redlin, and Watson): This textbook covers advanced concepts that build on basic skills, offering in-depth explanations and practice problems.
- Algebra 1 Study Guide (by Michael Kelley): A practical guide specifically designed for students studying introductory algebra. This guide includes clear explanations, sample problems, and practice exercises.
These resources are valuable for reinforcing your understanding of key concepts and ensuring that you have the support you need to succeed. Whether you prefer interactive online exercises, self-paced textbook learning, or video explanations, there is a tool that will work for you.