Mastering the fundamentals of mathematical problem-solving requires a structured approach that builds understanding progressively. In this guide, we explore essential concepts that lay the foundation for more advanced studies. Each topic is broken down into manageable sections, providing clear explanations and examples to ensure a thorough comprehension of the material.
Students often struggle with specific challenges, but by focusing on step-by-step techniques, it’s possible to overcome common obstacles. Whether you’re tackling equations or working through complex expressions, this resource offers the support needed to approach problems with confidence. Practical tips, along with targeted exercises, help solidify key skills and boost proficiency.
Throughout the sections, focus is placed on understanding core principles rather than just memorizing solutions. With each concept explored, learners can gain a deeper appreciation of how mathematical tools apply to real-world scenarios, paving the way for further academic success.
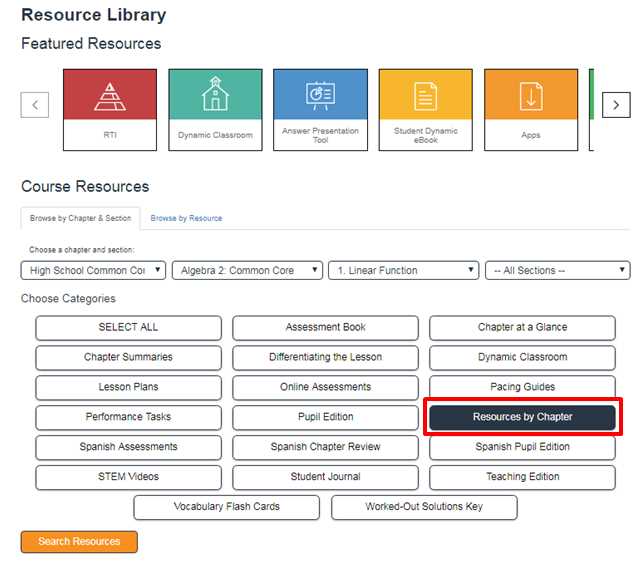
Big Ideas Math Algebra 1 Resources
Effective learning tools are crucial for grasping the essential principles of mathematics. To ensure a solid foundation, various learning aids are available that help break down complex topics into easily understandable sections. These materials offer in-depth explanations, step-by-step solutions, and interactive activities, making it easier for students to master core concepts and techniques.
In this section, a wide range of materials is presented to support learners through each stage of their journey. From detailed guides that clarify key mathematical ideas to practice exercises that reinforce skills, every aspect is designed to enhance understanding and application. These aids ensure that no matter the level of difficulty, students can work at their own pace and progressively build confidence in their problem-solving abilities.
Students can also benefit from additional tools that provide instant feedback and targeted explanations for areas that require extra attention. Whether tackling basic problems or more intricate equations, these materials offer continuous support to foster deeper engagement with the content and accelerate progress.
Overview of Algebra 1 Curriculum
The curriculum for introductory mathematics is designed to introduce fundamental concepts and techniques essential for solving a variety of numerical problems. It builds progressively from simple operations to more complex expressions and equations, providing a clear path toward mastering essential skills. This structure allows learners to gain a solid understanding of core principles before moving on to advanced topics.
Throughout the course, students are guided through various concepts such as solving linear equations, understanding functions, and working with polynomials. Each unit focuses on a specific area, ensuring that learners can follow along and grasp the material at their own pace. By the end of the course, students will have developed critical problem-solving skills applicable in various real-life situations.
Key Concepts and Skills
| Concept | Description |
|---|---|
| Linear Equations | Understanding how to solve equations involving variables and constants. |
| Functions | Introduction to functions, their properties, and graphing techniques. |
| Polynomials | Learning how to work with polynomial expressions and factor them. |
Learning Objectives

The main goal of this course is to equip students with the ability to tackle basic and intermediate mathematical problems with confidence. By focusing on the most relevant skills and techniques, the course prepares students to apply their knowledge in both academic and practical contexts. The curriculum emphasizes understanding and applying concepts rather than memorizing formulas, ensuring that students develop a deeper comprehension of the subject.
Understanding Key Concepts in Algebra

Grasping the foundational principles of mathematics is essential for progressing through more complex topics. Key concepts form the building blocks that allow students to approach a wide variety of problems with a clear understanding. These concepts include operations with variables, solving equations, and recognizing patterns within numerical relationships.
As learners advance, they develop a deeper comprehension of how different concepts interconnect. For example, understanding how to manipulate expressions is directly related to solving equations and graphing functions. Mastering these ideas allows for greater flexibility and problem-solving efficiency, providing the tools necessary to tackle more advanced material.
Essential Techniques for Problem Solving
Among the core techniques are methods for simplifying expressions, solving for unknowns, and using properties of operations. These methods are not only applicable in academic settings but are also vital in real-world problem-solving scenarios. By practicing these techniques, students enhance their analytical thinking and gain confidence in approaching challenges.
Key Areas of Focus
| Concept | Importance |
|---|---|
| Linear Equations | These form the foundation for solving more complex relationships. |
| Functions | Understanding functions is critical for graphing and analyzing data. |
| Polynomials | Key for simplifying and factoring more complex expressions. |
Chapter 1: Foundations of Algebra

The initial stage of any mathematical study involves understanding the basic principles that form the foundation of more advanced topics. This first section introduces the essential tools and techniques necessary for solving problems and manipulating expressions. The focus is on developing a clear understanding of numbers, variables, and the operations that govern them, providing students with a solid starting point for further learning.
At this stage, students learn how to work with simple equations, understand the properties of numbers, and become familiar with the concept of variables. These building blocks are crucial for progressing through more complex mathematical challenges. Mastering these core principles is vital for success in any future studies involving problem-solving and mathematical reasoning.
| Concept | Key Skills |
|---|---|
| Variables and Expressions | Understanding how to represent unknowns and simplify expressions. |
| Order of Operations | Applying the correct sequence of operations to solve problems. |
| Equations | Solving for unknowns by balancing both sides of an equation. |
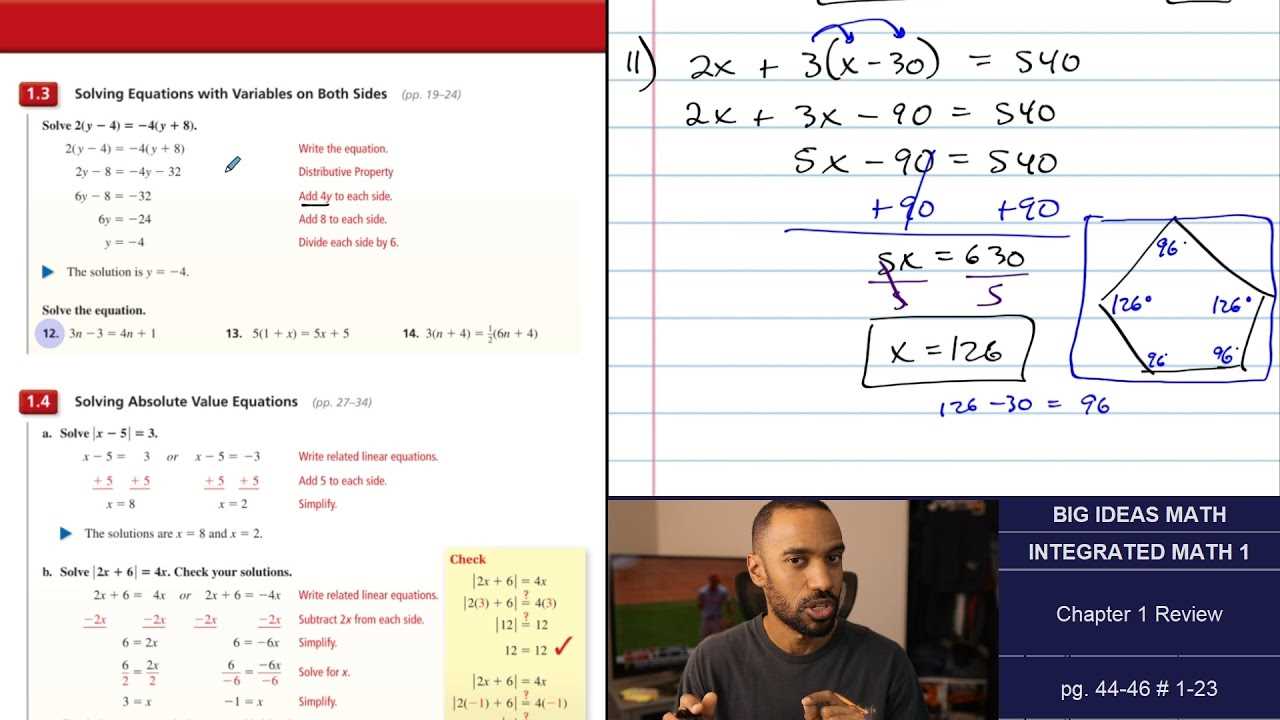
Solving Linear Equations in Chapter 2

In this section, the focus shifts to solving equations involving variables, where the goal is to find the value of an unknown that satisfies the given relationship. This is a fundamental skill that builds the foundation for more complex problem-solving. By understanding how to manipulate and isolate variables, students can unlock the solutions to various mathematical scenarios.
Throughout this topic, learners will explore various methods for solving linear equations, including using addition, subtraction, multiplication, and division to isolate the variable. The process requires balancing both sides of the equation while following specific rules to ensure accuracy. Mastering this technique is key for advancing to more sophisticated types of equations and mathematical reasoning.
| Step | Action |
|---|---|
| 1 | Identify the equation and isolate the variable term. |
| 2 | Perform operations to simplify both sides. |
| 3 | Solve for the unknown by isolating it completely. |
Graphing and Slope in Chapter 3
Understanding how to visually represent relationships between variables is essential in solving real-world problems. This section introduces the concept of graphing equations on a coordinate plane, providing a visual tool for analyzing mathematical relationships. By plotting points and drawing lines, students can observe the behavior of different equations and make predictions based on their graphs.
The concept of slope plays a critical role in understanding how two variables change in relation to each other. The slope measures the steepness of a line and provides important insights into the rate of change between the two variables. By mastering how to calculate and interpret slope, students can better understand trends and patterns, which is useful for both mathematical and practical applications.
Graphing equations involves plotting points on a grid and drawing a line that represents the equation’s relationship. This visual approach helps clarify how changes in one variable affect the other. Once the graph is created, the slope is determined by calculating the ratio of vertical change to horizontal change between two points on the line.
| Step | Action |
|---|---|
| 1 | Plot points based on the equation. |
| 2 | Draw a line through the points to represent the relationship. |
| 3 | Calculate the slope by finding the ratio of rise over run. |
Quadratic Functions in Chapter 4
In this section, the focus shifts to more complex equations, specifically those that represent parabolic relationships. Quadratic functions introduce a new level of problem-solving, where the highest exponent of the variable is squared. These functions are crucial for understanding curves and their properties, which appear frequently in real-world situations, such as projectile motion and optimization problems.
Quadratic equations can be solved in several ways, including factoring, completing the square, and using the quadratic formula. Each method offers a different approach for finding the roots of the equation, or the points where the curve intersects the x-axis. By mastering these techniques, students gain the ability to solve and interpret parabolic relationships accurately and efficiently.
Key Features of Quadratic Functions
Vertex: The highest or lowest point on the graph, depending on the direction of the parabola. Understanding the vertex is key to graphing and analyzing the function’s behavior.
Axis of Symmetry: A vertical line that divides the parabola into two equal parts. This line passes through the vertex and helps in graphing and solving equations.
Solving Quadratic Equations
| Method | Procedure |
|---|---|
| Factoring | Rewrite the quadratic equation as a product of two binomials and solve for the variable. |
| Completing the Square | Rewrite the equation in perfect square form, then solve for the variable. |
| Quadratic Formula | Use the formula x = (-b ± v(b? – 4ac)) / 2a to find the solutions. |
Exponents and Polynomials Explained
Understanding exponents and polynomials is fundamental in simplifying and solving mathematical expressions. Exponents refer to the number of times a number is multiplied by itself, while polynomials are algebraic expressions that involve sums of terms with variables raised to various powers. These concepts are essential for solving equations and working with more complex mathematical models.
Exponents make it easier to express repeated multiplication. For example, instead of writing out 3 ? 3 ? 3, we simply use 3?. This shorthand allows for easier manipulation of numbers in equations and functions. Polynomials, on the other hand, are combinations of variables, constants, and exponents, and can represent a wide range of real-world situations, such as growth rates and optimization problems.
Key Concepts of Exponents
- Product of Powers: When multiplying two expressions with the same base, add their exponents: a^m ? a^n = a^(m+n).
- Power of a Power: To raise a power to another power, multiply the exponents: (a^m)^n = a^(m?n).
- Zero Exponent: Any number raised to the zero power equals one: a^0 = 1.
Understanding Polynomials
Polynomials can have one or more terms, each containing a variable raised to a non-negative integer exponent. For example, the expression 3x? + 2x + 1 is a polynomial with three terms. The highest exponent in the polynomial indicates its degree, which is important when classifying the polynomial.
- Monomials: A polynomial with just one term (e.g., 5x or 7).
- Binomials: A polynomial with two terms (e.g., x? + 3x).
- Trinomials: A polynomial with three terms (e.g., 2x? + 5x + 3).
By mastering exponents and polynomials, students can simplify complex expressions, factor equations, and solve a variety of problems in higher-level mathematics.
Factoring Techniques for Algebra 1

Factoring is a critical skill for simplifying and solving equations, particularly when working with polynomials. By breaking down complex expressions into simpler components, factoring makes it possible to find solutions more efficiently. This process helps in solving quadratic equations and is a foundational technique in many areas of mathematics.
In this section, we explore different strategies for factoring, each suited to particular types of expressions. Whether you’re working with common factors, special products, or quadratic expressions, mastering these techniques is key to improving problem-solving abilities. Below are the most widely used factoring methods that will help in simplifying expressions.
Key Factoring Methods
- Factoring out the Greatest Common Factor (GCF): This is the first step in simplifying many expressions. By identifying the largest factor common to all terms, you can factor it out and make the remaining expression easier to work with. For example, in 6x? + 12x, the GCF is 6, so the factored form is 6(x? + 2x).
- Factoring by Grouping: This method is used when you have four terms in the expression. You group the terms in pairs and factor out the common factor from each pair. After factoring, you can factor out the remaining common binomial. For instance, x? + 5x + 2x + 10 can be grouped as (x? + 5x) + (2x + 10), then factored as x(x + 5) + 2(x + 5), and finally factored further to (x + 5)(x + 2).
- Factoring Trinomials: When dealing with quadratic expressions in the form of ax? + bx + c, the goal is to find two binomials whose product gives the original trinomial. The method typically involves finding two numbers that multiply to ac and add to b. For example, in x? + 5x + 6, the numbers 2 and 3 multiply to 6 and add to 5, so the factored form is (x + 2)(x + 3).
Additional Techniques for Special Cases
- Difference of Squares: This applies when you have a binomial of the form a? – b?. It can always be factored as (a – b)(a + b). For example, x? – 9 factors to (x – 3)(x + 3).
- Perfect Square Trinomial: A trinomial that is the square of a binomial. For example, x? + 6x + 9 factors to (x + 3)?.
By mastering these factoring techniques, students can simplify expressions and solve equations more effectively, laying the groundwork for tackling more complex mathematical problems.
Simplifying Expressions and Equations

Simplifying expressions and equations is an essential skill for solving mathematical problems. The goal is to reduce complex expressions to their simplest form, making it easier to find solutions and understand relationships between variables. This process involves combining like terms, eliminating unnecessary parentheses, and applying fundamental properties of operations. Mastering these techniques helps build a strong foundation for more advanced topics in mathematics.
By simplifying expressions, you can reduce the number of steps required to solve an equation. This approach not only speeds up problem-solving but also makes it easier to spot patterns and relationships within the expression. Below, we explore the basic techniques used to simplify various types of mathematical expressions and equations.
Combining Like Terms
When simplifying an expression, the first step is to combine like terms. Like terms are terms that have the same variable raised to the same power. For instance, in the expression 3x + 5x – 2y + 4y, the like terms are 3x and 5x, and -2y and 4y. Simplifying the expression gives 8x + 2y.
Eliminating Parentheses
Another key aspect of simplifying is removing parentheses. When you encounter parentheses in an expression, use the distributive property to eliminate them. For example, in the expression 2(x + 3), you distribute the 2 to both terms inside the parentheses, resulting in 2x + 6. This makes it easier to work with the expression in subsequent steps.
By mastering these basic techniques, you can simplify even the most complex expressions and equations, making it easier to solve and understand mathematical relationships.
Working with Rational Expressions
Working with rational expressions involves simplifying, manipulating, and solving equations that contain fractions with polynomials in the numerator and denominator. These expressions are similar to basic fractions but often require more advanced techniques to handle their complexity. Understanding how to work with rational expressions is crucial for solving equations and inequalities that involve variables.
To work with rational expressions effectively, you must be familiar with several key processes, such as simplifying complex fractions, factoring the numerator and denominator, and determining when certain values would make the expression undefined. Below, we will explore the essential steps for simplifying and solving equations involving rational expressions.
Simplifying Rational Expressions
The first step in working with rational expressions is simplifying them. This involves canceling common factors between the numerator and denominator. For example, in the expression (2x? + 6x) / (4x), you can factor out the common factor of 2x from both the numerator and denominator. This simplifies the expression to (x + 3) / 2.
Multiplying and Dividing Rational Expressions
When multiplying rational expressions, you multiply the numerators together and the denominators together. For instance, (2x / 3) * (4 / x?) results in 8x / 3x?, which can be simplified further to 8 / 3x.
Similarly, when dividing rational expressions, multiply the first expression by the reciprocal of the second. For example, (3x / 5) ? (2 / x) becomes (3x / 5) * (x / 2), which simplifies to 3x? / 10.
- Factor both the numerator and denominator: Factor polynomials to identify common factors that can be canceled out.
- Check for restrictions: Identify values of the variable that would make the denominator zero, as these values are not allowed in rational expressions.
By following these techniques and practicing them regularly, you can solve complex problems involving rational expressions with greater ease and accuracy.
Systems of Equations and Inequalities
Solving systems of equations and inequalities involves finding values that satisfy multiple conditions at the same time. These problems often arise when dealing with real-world scenarios where two or more relationships need to be solved simultaneously. Understanding how to approach and solve these systems is crucial for dealing with complex problems in various mathematical contexts.
In this section, we will explore the methods used to solve systems, both for equations and inequalities. The goal is to find the point(s) where the expressions intersect, or determine the range of values that satisfy all conditions involved. There are several methods, including substitution, elimination, and graphing, each of which can be applied based on the specific problem at hand.
Solving Systems of Equations
When solving systems of equations, the objective is to find a pair of values for the variables that satisfy both equations simultaneously. The most common methods for solving such systems are substitution and elimination.
- Substitution Method: In this approach, solve one equation for one variable and substitute this expression into the other equation. This results in a single equation with one variable, which can be solved easily.
- Elimination Method: The elimination method involves adding or subtracting the equations to eliminate one variable, simplifying the system to a single equation that can be solved for the remaining variable.
Solving Systems of Inequalities
Solving systems of inequalities requires finding the region where all inequalities are true. Unlike equations, the solution is often a range or area rather than a single point. Graphing is one of the most effective methods for visualizing the solution.
- Graphing Method: To graph the system, plot each inequality on the coordinate plane. The solution to the system is the region where the shaded areas of all inequalities overlap.
- Substitution or Elimination: In some cases, you may apply substitution or elimination methods to solve systems of inequalities by first converting them into equalities or finding boundary points.
By mastering these techniques, you will be able to solve a wide range of systems, both linear and nonlinear, with confidence and accuracy.
Solving Word Problems in Algebra
Word problems often present mathematical situations in real-life contexts. The goal is to translate the language of the problem into mathematical expressions, then solve for the unknowns. These types of problems require logical thinking, interpretation of given information, and applying appropriate mathematical methods to find a solution.
To solve word problems, it is essential to break down the problem step by step, identifying key elements such as variables, relationships, and conditions. Once the problem is understood, it can be transformed into an equation or system of equations that can be solved using various techniques.
Steps for Solving Word Problems
The process of solving word problems typically follows these steps:
- Understand the Problem: Read the problem carefully to grasp what is being asked. Identify the quantities involved and their relationships.
- Define Variables: Assign variables to the unknowns in the problem. Make sure each variable corresponds to a specific quantity.
- Write Equations: Translate the relationships and conditions into equations. Use mathematical operations to represent the problem’s situation.
- Solve the Equations: Use appropriate methods, such as substitution, elimination, or graphing, to solve the equations and find the values of the variables.
- Check the Solution: Verify that the solution satisfies all the conditions of the problem. If necessary, recheck your work and ensure that the answer makes sense in the context of the problem.
Common Types of Word Problems
There are many types of word problems that involve different mathematical concepts. Some of the most common include:
- Mixture Problems: These involve combining different substances and determining the resulting mixture’s properties.
- Distance, Rate, and Time Problems: These problems involve calculating the relationship between distance, speed, and time.
- Age Problems: These problems involve determining the ages of people or objects based on their relationships at different points in time.
- Work Problems: These involve calculating the time it takes for one or more workers to complete a task, given their rates of work.
By practicing these steps and types of problems, you can become proficient in translating real-world situations into solvable mathematical equations, enhancing both your problem-solving skills and mathematical understanding.
Common Mistakes to Avoid in Algebra
When working through mathematical problems, there are several common errors that students often make, especially when dealing with equations, expressions, and operations. These mistakes can lead to incorrect solutions and a misunderstanding of key concepts. By recognizing and avoiding these pitfalls, you can significantly improve your problem-solving accuracy and overall understanding.
Understanding where mistakes commonly occur is an important part of mastering the subject. Many errors result from oversights, misinterpretation of the problem, or improper application of rules and operations. Here are some of the most frequent mistakes to be mindful of when solving problems.
Common Errors to Watch Out For
- Incorrectly Applying the Distributive Property: A common mistake is distributing terms incorrectly. For example, when distributing a negative sign across parentheses, it’s important to change the sign of each term inside.
- Sign Errors: Misplacing or forgetting negative signs can lead to significant mistakes. Always double-check signs when performing operations like addition or subtraction.
- Confusing Multiplication and Addition: Some students mix up multiplication and addition operations when solving expressions. Remember, multiplication distributes over addition, but addition does not distribute over multiplication.
- Incorrectly Solving for Variables: When isolating a variable, it’s crucial to perform the same operation on both sides of the equation. Failing to do so can result in an incorrect answer.
- Misinterpreting Word Problems: Word problems often involve translating sentences into mathematical equations. The most common mistake is misreading the problem or overlooking key information.
How to Avoid These Mistakes
To minimize these common errors, here are a few helpful tips:
- Review Basic Operations: Make sure you have a strong understanding of fundamental operations like addition, subtraction, multiplication, and division. This foundation is key to avoiding simple mistakes.
- Check Your Work: After solving a problem, take the time to review each step and ensure that you didn’t overlook any details. Double-check signs, operations, and final answers.
- Practice Regularly: Frequent practice with different problem types helps to reinforce your skills and make the process more intuitive, reducing the likelihood of errors.
- Seek Clarification: If you’re unsure about any concept, ask for help or look for additional resources to deepen your understanding.
By staying aware of these common mistakes and following these tips, you can enhance your problem-solving skills and avoid unnecessary confusion in your studies.
Tips for Studying Algebra 1 Effectively
To excel in any mathematical discipline, a strategic approach to studying is crucial. Effective study habits help solidify understanding, enhance problem-solving skills, and reduce the stress of tackling complex topics. Whether you are reviewing fundamental concepts or diving into more advanced problems, applying the right techniques can make a significant difference in your academic performance.
The key to success lies in consistent practice, active learning, and focusing on areas where you need the most improvement. Below are some tips to help you study and master the subject more effectively.
Effective Study Techniques
- Practice Regularly: Consistent practice is essential to mastering any skill. Set aside time each day to work through problems, review concepts, and refine your techniques.
- Focus on Understanding, Not Just Memorization: Rather than simply memorizing formulas and rules, aim to understand the logic behind each concept. This deeper understanding will help you apply your knowledge to a variety of problems.
- Break Down Complex Problems: When faced with a difficult problem, break it into smaller, manageable steps. Tackling one step at a time can prevent overwhelm and ensure you’re addressing each part correctly.
- Use Different Learning Resources: Don’t limit yourself to just one textbook or set of notes. Explore online tutorials, videos, and practice problems to reinforce your learning from multiple angles.
- Group Study Sessions: Collaborating with peers in study groups can be highly beneficial. Explaining concepts to others reinforces your own understanding, and group discussions can provide new insights.
Maximizing Your Study Time

- Create a Study Schedule: Plan your study sessions to ensure you’re reviewing all topics, especially those you find challenging. Consistency is key, so make studying a daily habit.
- Stay Organized: Keep your notes, assignments, and practice materials well-organized. Use color-coding or digital tools to track your progress and identify areas that need more attention.
- Focus on Weak Areas: Identify which topics you find most difficult and dedicate extra time to them. By addressing weak points early on, you’ll avoid falling behind later in the course.
- Stay Positive and Patient: Learning complex concepts takes time, and it’s normal to encounter setbacks. Stay patient with yourself, maintain a positive attitude, and celebrate small victories along the way.
By applying these tips and developing good study habits, you’ll be well on your way to mastering the subject and achieving academic success.
Additional Resources for Algebra Mastery

To fully grasp the concepts of the subject, it’s important to complement textbook learning with supplementary materials. Whether you’re looking for extra practice, detailed explanations, or interactive tools, there are many options available to help reinforce your understanding. These additional materials can help you build confidence and improve your problem-solving abilities in a variety of ways.
Below are some valuable resources that can support your learning journey, each offering unique ways to enhance your comprehension and skills.
Supplementary Learning Platforms
| Platform | Description | Type of Content |
|---|---|---|
| Online Tutoring Services | These platforms offer one-on-one sessions with experts who can guide you through difficult topics. | Live Tutoring, Practice Problems |
| Interactive Websites | Websites that provide step-by-step tutorials, quizzes, and instant feedback to test your understanding. | Interactive Exercises, Video Tutorials |
| Video Lessons | These video resources break down complex topics into easy-to-understand segments. | Video Explanations, Practice Problems |
| Study Apps | Mobile applications that let you practice and review concepts on the go. | Flashcards, Quizzes, Concept Reviews |
Books and Print Materials
- Workbooks and Practice Books: These provide additional problems and solutions to help reinforce what you’ve learned in class.
- Concept Review Guides: Books that offer concise reviews of important principles and techniques with plenty of examples.
- Problem-Solving Books: These books focus specifically on solving a variety of problems to enhance critical thinking and application of concepts.
By utilizing these resources, you can gain deeper insights into the subject, practice more effectively, and address areas of difficulty. The combination of varied content types–from interactive tools to written guides–ensures that you’ll find methods that suit your learning style and pace.