Advanced problem-solving in mathematics requires a deep understanding of various principles and techniques. Mastering these concepts enables students to navigate complex equations and functions with ease. This section focuses on providing clear and structured guidance to help learners develop the skills needed to succeed in higher-level mathematical studies.
Effective problem-solving strategies are essential for tackling difficult exercises. By breaking down complex tasks into simpler steps, students can build confidence and accuracy. Understanding the underlying concepts behind each problem is key to finding the most efficient solutions.
Whether working with functions, equations, or graphs, having a solid foundation in these core areas is crucial. With the right approach and consistent practice, anyone can improve their proficiency and tackle even the most challenging mathematical problems with success.
Advanced Problem Solving Guide for Algebra 2
This section offers a comprehensive approach to understanding and solving problems in advanced mathematics. It presents essential tools and methods that will help students build confidence and proficiency in handling a wide range of mathematical topics. By focusing on key techniques and step-by-step solutions, learners can strengthen their grasp of critical concepts and improve their problem-solving abilities.
Core Topics and Concepts
Mastering core mathematical functions is essential for tackling more complex problems. Topics such as quadratic equations, exponential functions, and polynomial expressions form the foundation of this level of study. Understanding how these areas connect and apply to real-world scenarios makes solving them much easier and more intuitive.
Building Strong Problem-Solving Skills
To effectively solve problems, it’s crucial to develop strong analytical skills. This can be achieved through consistent practice and application of problem-solving strategies. Breaking down equations into manageable parts and focusing on one step at a time can greatly improve both speed and accuracy when solving complex exercises.
Overview of Algebra 2 Concepts
This section provides a broad understanding of the fundamental concepts that are covered in advanced mathematical studies. The focus is on key topics that form the foundation of higher-level problem-solving, helping students connect various principles and improve their overall skills. A solid grasp of these concepts is crucial for progressing through more challenging problems and applications.
Key Functions and Equations
At the core of advanced mathematics lies an understanding of different types of functions, including linear, quadratic, and exponential forms. These functions are the building blocks for more complex operations, and mastering them is essential for solving a wide range of mathematical problems.
Exploring Systems and Graphs
Systems of equations and graphing techniques play a significant role in algebraic problem-solving. Learning how to visualize and interpret these systems allows for easier solutions and a deeper understanding of mathematical relationships. Strong graphing skills are particularly useful for tackling word problems and real-world applications.
Mastering Key Algebraic Functions
Developing a deep understanding of essential mathematical functions is critical for solving complex problems. These functions are the building blocks for many equations and are integral to various aspects of higher-level studies. Mastering these key functions allows students to approach challenges with confidence and precision.
Several core functions play a central role in this stage of mathematical learning. These include:
- Linear functions: Fundamental for understanding the relationships between variables in a straight line.
- Quadratic functions: Crucial for solving equations involving squared terms and understanding their graphical representations.
- Exponential functions: Used to model growth and decay in a variety of real-world applications.
- Rational functions: Help solve problems involving fractions of polynomials.
To master these functions, it’s essential to practice recognizing their forms, understanding their behaviors, and solving related equations. This foundational knowledge will serve as the basis for solving more complicated systems and real-world problems.
Step-by-Step Solutions for Exercises
Breaking down complex exercises into smaller, manageable steps is crucial for mastering advanced problem-solving. By carefully following a clear sequence of operations, students can effectively approach each challenge, ensuring a deeper understanding of the methods involved. This structured approach helps prevent mistakes and builds confidence in tackling difficult problems.
Approach to Solving Equations
When faced with an equation, the first step is always to simplify both sides as much as possible. This could involve factoring, expanding, or combining like terms. Once simplified, applying appropriate mathematical rules and operations will lead to the solution. Checking the solution is an essential final step to ensure accuracy.
Graphing and Analyzing Functions
Graphing is another essential skill. It involves plotting key points based on the equation and analyzing how the graph behaves. Understanding the general shape of the graph, its intercepts, and any asymptotes helps provide valuable insights into the equation’s behavior. Clear visualization aids in solving problems and interpreting real-world applications.
Understanding Quadratic Equations

Quadratic equations are one of the most important topics in advanced mathematics, as they often appear in various real-life applications. These types of equations involve squared terms and typically result in parabolic graphs. Understanding how to solve and manipulate these equations is essential for progressing in more complex mathematical problems.
To solve quadratic equations, different methods can be used, including factoring, completing the square, and applying the quadratic formula. Each of these techniques offers a systematic way to find the solutions, whether they are real or imaginary. By mastering these methods, students can approach quadratic problems with confidence and precision.
Solving Systems of Equations Easily
Solving systems of equations can initially seem challenging, but by breaking them down into simpler steps, the process becomes much more manageable. A system typically consists of two or more equations that must be solved simultaneously. The goal is to find the values of the variables that satisfy all the equations at once.
There are several methods for solving these systems effectively:
- Substitution method: Solve one equation for one variable and then substitute that expression into the other equation.
- Elimination method: Add or subtract equations to eliminate one variable, making it easier to solve for the remaining one.
- Graphing method: Graph each equation on the same coordinate plane and find the point of intersection, which represents the solution.
Each method has its advantages, and the best approach often depends on the complexity of the system. With consistent practice, students can quickly identify which method works best for a given problem and solve it efficiently.
Exploring Polynomials and Their Roots
Polynomials are powerful mathematical expressions that involve multiple terms, typically with varying powers of a variable. Understanding how to work with these expressions and find their roots is essential for solving complex problems. The roots, or solutions, of a polynomial are the values of the variable that make the expression equal to zero. Exploring these roots and their behavior provides insight into the nature of the polynomial and its graph.
To better understand polynomials and their roots, consider the general form of a polynomial:
| Degree | Form of Polynomial | Example |
|---|---|---|
| 1st Degree | Linear | 3x + 5 = 0 |
| 2nd Degree | Quadratic | x² – 4 = 0 |
| 3rd Degree | Cubic | x³ + 2x – 3 = 0 |
Finding the roots of these polynomials often involves factoring, using the quadratic formula for quadratics, or applying numerical methods for higher degrees. The number of roots corresponds to the degree of the polynomial, and these roots can be real or complex. Analyzing the nature of the roots helps in understanding the polynomial’s behavior, especially when graphed.
Mastering Rational Expressions
Rational expressions involve ratios of two polynomials and are key in solving various complex problems. By understanding how to simplify, manipulate, and solve these expressions, students can approach a wide range of equations with confidence. Mastery of rational expressions not only enhances problem-solving skills but also deepens understanding of the relationships between different types of mathematical functions.
To master these expressions, it’s important to focus on the following core steps:
- Simplifying expressions: Reduce the expression by factoring both the numerator and the denominator, and cancel out common factors.
- Finding excluded values: Identify values that would make the denominator equal to zero, as these values cannot be part of the solution set.
- Adding or subtracting rational expressions: To add or subtract, first find a common denominator, then combine the numerators.
- Multiplying and dividing rational expressions: Multiply the numerators and denominators separately, simplifying the result as much as possible.
Through consistent practice and application of these techniques, solving complex rational expressions becomes a systematic and manageable task. Understanding these fundamental operations ensures a solid foundation for tackling more advanced mathematical concepts.
Strategies for Exponential Functions
Exponential functions are a critical component of mathematical problem-solving, especially when dealing with growth and decay models. These functions describe situations where the rate of change is proportional to the current value, making them particularly useful in fields such as finance, biology, and physics. Understanding the key strategies for solving exponential equations is essential for accurately modeling and interpreting real-world phenomena.
Key Techniques for Solving Exponential Equations
When solving exponential equations, one of the first strategies is to rewrite both sides of the equation with the same base. This allows for direct comparison of the exponents, simplifying the equation. If the bases cannot be matched, logarithms provide a powerful tool for solving equations involving exponents.
Graphing Exponential Functions
Graphing exponential functions helps visualize their behavior and understand their characteristics, such as growth and decay rates. The general shape of the graph depends on whether the base is greater than or less than one. Understanding the horizontal asymptote is also crucial, as it shows the limiting value that the function approaches as the variable increases.
Working with Logarithmic Equations
Logarithmic equations are fundamental in solving problems involving exponential relationships. These equations allow for the reversal of exponential functions, transforming multiplicative processes into additive ones. Mastering logarithmic equations is essential for simplifying complex expressions and solving for unknown variables in a variety of contexts, such as growth, decay, and financial modeling.
When solving logarithmic equations, the primary goal is to isolate the logarithmic expression before applying inverse operations. This may involve using logarithmic properties, such as the product, quotient, or power rules, to simplify the equation. In some cases, it may be necessary to rewrite the equation in exponential form to better understand the relationship between the terms and find a solution.
Tips for Solving Radical Equations
Solving radical equations can often seem daunting, but with the right approach, they become more manageable. These equations involve expressions with roots, such as square roots or cube roots, which add an extra layer of complexity compared to simple linear or quadratic equations. The key to solving these equations is to eliminate the radical and simplify the problem step by step.
Isolate the Radical Expression
To begin solving radical equations, the first step is usually to isolate the radical expression on one side of the equation. This allows for a clearer path to removing the root and simplifies the process. Once the radical is isolated, the next step is to eliminate it by raising both sides of the equation to the appropriate power that matches the root.
Check for Extraneous Solutions
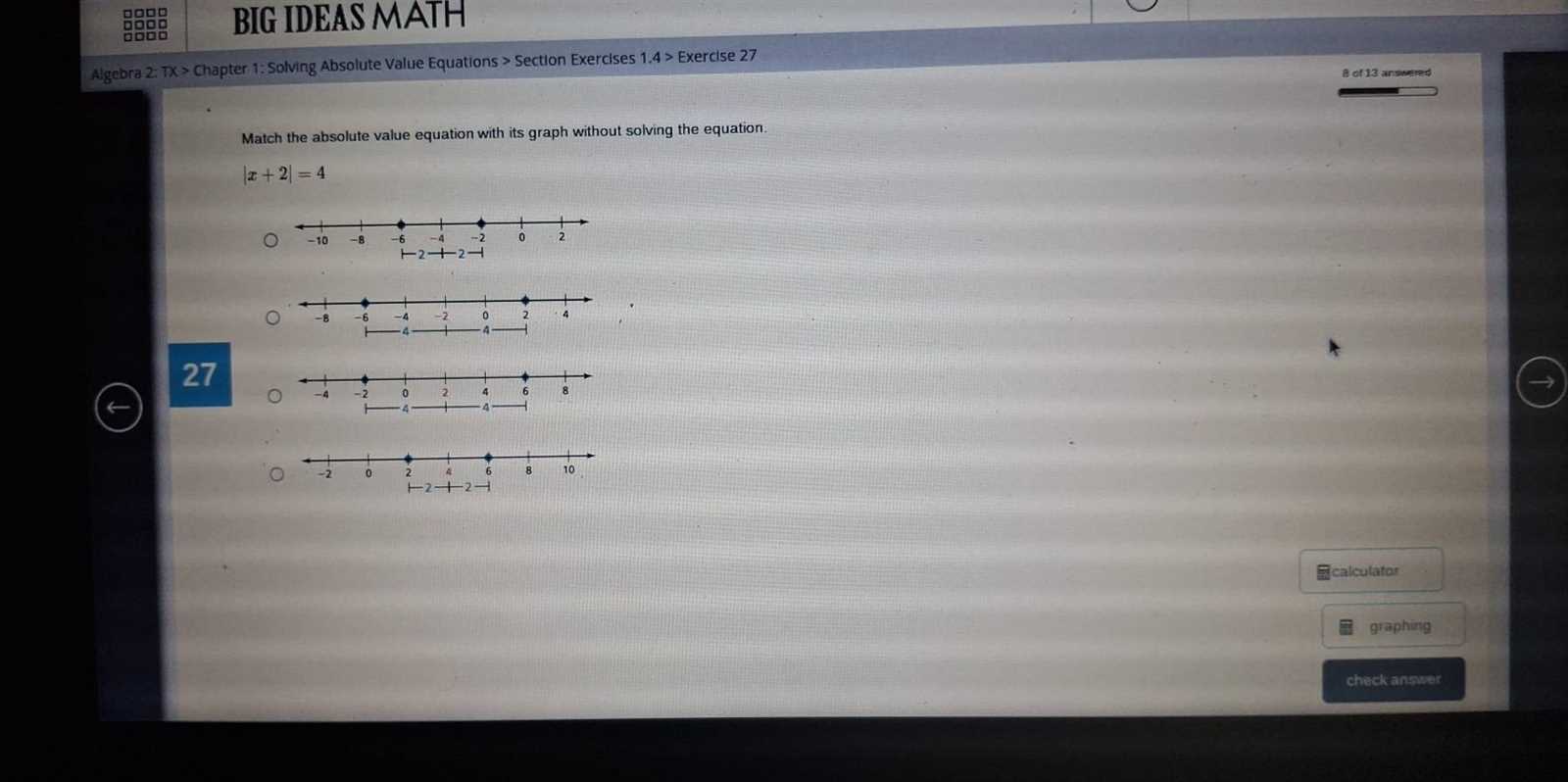
After solving the equation, it is important to check for extraneous solutions. These are solutions that may arise from the algebraic manipulation but do not satisfy the original equation. To verify the solutions, substitute them back into the original equation to ensure they hold true. This step is crucial, as it prevents incorrect solutions from being included in the final answer.
Understanding Conic Sections
Conic sections are curves that are formed by the intersection of a plane and a cone. These curves play a significant role in geometry and can describe various real-world phenomena such as planetary orbits, light reflection, and sound waves. Understanding the different types of conic sections and their properties allows for deeper insights into both theoretical and applied mathematics.
Types of Conic Sections
There are four primary types of conic sections, each with its own unique characteristics:
| Conic Section | Shape | Equation |
|---|---|---|
| Circle | A round shape where all points are equidistant from the center. | x² + y² = r² |
| Ellipse | An elongated circle, with two focal points. | (x²/a²) + (y²/b²) = 1 |
| Parabola | A U-shaped curve that opens either upward, downward, left, or right. | y = ax² + bx + c |
| Hyperbola | A curve with two disconnected branches, formed by the intersection of a plane and a cone. | (x²/a²) – (y²/b²) = 1 |
Applications of Conic Sections
Conic sections have a wide range of applications in various fields. For example, ellipses are often used in the study of planetary motion, while parabolas appear in the design of satellite dishes and reflectors. Hyperbolas are important in understanding certain physical systems, such as the paths of objects in space. Understanding these shapes and their properties is essential for solving many complex problems in both mathematics and science.
Graphing Complex Functions Simplified

Graphing complex functions can appear intimidating due to their intricate nature, but with the right approach, it becomes a much more manageable task. These functions often involve both real and imaginary components, which are essential for understanding behaviors in multiple dimensions. By breaking down the process into key steps and utilizing appropriate techniques, you can graph these functions with greater clarity and accuracy.
Key Steps to Simplify the Graphing Process
To make graphing complex functions easier, follow these steps:
- Identify the Function’s Components: Start by recognizing the real and imaginary parts of the function. This helps you separate what will be plotted on the real axis versus the imaginary axis.
- Choose the Right Coordinates: For complex functions, you typically work in a coordinate system called the complex plane, where the horizontal axis represents the real component and the vertical axis represents the imaginary component.
- Use Graphing Tools: Graphing tools like graphing calculators or software can assist in visualizing the functions more easily, especially for functions that involve higher complexities.
- Plot Key Points: Determine critical points such as intercepts, asymptotes, or other features of the function that can help you understand its behavior over a range of values.
Common Techniques for Different Types of Functions
When graphing specific types of complex functions, certain techniques may be more effective:
- For Polynomial Functions: Look for zeros of the polynomial, which indicate where the graph crosses the real axis.
- For Rational Functions: Identify vertical and horizontal asymptotes to understand how the graph behaves near specific values.
- For Trigonometric Functions: Focus on periodicity and symmetry to determine how the function oscillates within the complex plane.
With consistent practice and a strategic approach, graphing complex functions becomes a process of identifying patterns and applying methods that simplify the interpretation of their behavior.
Identifying Functions and Their Properties

Understanding functions and their properties is a crucial part of analyzing mathematical relationships. Functions represent the relationship between two variables, where each input corresponds to exactly one output. By identifying the properties of different types of functions, you can predict their behavior and make calculations more efficient. These properties help classify functions, determine their graphs, and solve problems involving them.
Key Properties of Functions
Functions exhibit several key properties that define their behavior. Some of the most important properties include:
- Domain and Range: The domain represents all possible inputs for a function, while the range refers to all possible outputs. Identifying these is crucial for understanding the limits of a function’s behavior.
- Intercepts: The x- and y-intercepts show where the function crosses the axes. These points are essential for graphing and solving equations.
- Symmetry: Some functions have symmetry, such as even symmetry (symmetric with respect to the y-axis) or odd symmetry (symmetric with respect to the origin). Recognizing symmetry helps in simplifying analysis and graphing.
- Monotonicity: A function can be increasing, decreasing, or constant over certain intervals. Analyzing monotonicity gives insight into how the function behaves over time or distance.
Common Types of Functions

Functions can be categorized into different types, each with its own properties. Below is a summary of common types and their characteristics:
| Function Type | Key Properties |
|---|---|
| Linear Functions | Constant rate of change, straight line, no curvature. |
| Quadratic Functions | Parabolic shape, symmetric, has a vertex and axis of symmetry. |
| Exponential Functions | Rapid growth or decay, continuous increase or decrease. |
| Rational Functions | Defined as a ratio of polynomials, may have vertical and horizontal asymptotes. |
By recognizing the properties and characteristics of different functions, you can better understand how they behave in various mathematical contexts. This foundational knowledge is essential for solving complex problems and modeling real-world situations.
Key Tips for Word Problems
Word problems often require you to convert real-life situations into mathematical expressions. This process can be challenging because it involves understanding the context, identifying key elements, and applying the appropriate formulas. However, with a structured approach, tackling these problems becomes easier. By focusing on important details and following a clear problem-solving strategy, you can increase both your accuracy and confidence in solving such questions.
Here are some valuable strategies to help you effectively solve word problems:
- Read Carefully: Take your time to thoroughly read the problem. Pay attention to keywords that indicate operations, such as “sum,” “difference,” or “product,” and focus on what the problem is asking for.
- Highlight Key Information: Identify the known values and what you are required to find. Organize the given data and label unknowns clearly to avoid confusion later on.
- Set Up Variables: Represent unknown quantities with variables, such as x or y. This will help you create equations that describe the relationships in the problem.
- Write Equations: Translate the word problem into mathematical equations that reflect the relationships between the known and unknown values. This is crucial for finding the solution.
- Work Through Step-by-Step: Break the problem down into smaller steps. Solve one part at a time, ensuring that you fully understand each stage before moving on to the next.
- Review Your Solution: Once you’ve found an answer, double-check your calculations and make sure the result makes sense within the context of the problem. This helps prevent errors and confirms the accuracy of your solution.
By following these steps, you can approach word problems in a systematic way, which not only improves your chances of finding the correct answer but also helps you build problem-solving skills over time.
Common Mistakes and How to Avoid Them

When working through mathematical problems, it’s easy to make errors that can lead to incorrect answers. Some of these mistakes are common and can be avoided with careful attention to detail and proper strategies. Understanding these common pitfalls and how to prevent them can help you improve your accuracy and efficiency in solving problems.
1. Misinterpreting the Problem
One of the most frequent mistakes is misreading or misunderstanding the problem. Failing to identify the key information or the specific question being asked can result in incorrect equations and ultimately a wrong solution. To avoid this:
- Take your time to read the problem carefully. Pay attention to important details like units of measurement, keywords, and what the problem specifically asks for.
- Highlight key information as you read through the problem, such as numbers, variables, or phrases that define relationships between quantities.
2. Incorrect Use of Operations
Another common mistake involves incorrectly applying mathematical operations. This can happen, for example, when adding or subtracting terms that should be multiplied or divided, or when simplifying expressions incorrectly. To prevent this:
- Double-check the operations in the equation, particularly when dealing with negative signs or fractions.
- Use parentheses properly to ensure the correct order of operations, especially in complex expressions.
3. Forgetting to Simplify
Many students forget to simplify their final answers or intermediate steps. Leaving equations unsimplified can lead to unnecessarily complex answers, which might be difficult to check or compare. To avoid this:
- Always simplify your expressions before finalizing your answer, whether it’s factoring, reducing fractions, or combining like terms.
- Check for possible reductions at every step to ensure the solution is as simple as possible.
By being mindful of these mistakes and applying these simple strategies, you can avoid common errors and improve the accuracy of your solutions. Remember, attention to detail and careful problem-solving can make all the difference in achieving the correct result.
Utilizing Online Resources for Practice
In today’s digital age, there are a wealth of online platforms available that can significantly enhance your understanding and skills. These resources provide a variety of tools and exercises, allowing learners to practice concepts in a flexible and interactive environment. By using these online materials, students can reinforce what they’ve learned, explore new topics, and track their progress in real time.
1. Interactive Problem Solving

One of the greatest advantages of online resources is the ability to engage in interactive problem-solving. These platforms often offer instant feedback, which helps identify areas where you might need further practice. Some platforms even provide step-by-step solutions, allowing you to understand the process behind each step. To make the most of these resources:
- Focus on accuracy: Before moving on to the next problem, ensure that you fully understand each solution and identify any mistakes.
- Set a goal: Aim to complete a certain number of problems per day to build consistency in practice.
2. Exploring Tutorials and Video Lessons
In addition to exercises, many online platforms offer tutorials and video lessons that explain concepts in a detailed, easy-to-follow manner. These can be particularly helpful if you’re struggling with specific topics or need a refresher. Videos allow you to pause, rewind, and revisit complex explanations until you grasp the material. To benefit from these tutorials:
- Take notes: Jot down key concepts and examples as you watch to reinforce learning.
- Practice alongside: Try solving similar problems as you watch the videos to apply the concepts in real-time.
By integrating online tools into your learning routine, you can create a more engaging and effective study experience. These resources can help you master difficult topics, provide a deeper understanding of the material, and boost your confidence in solving problems independently.