In the world of personal finance and daily decision-making, numerical challenges are a common part of life. From budgeting to understanding prices, individuals are constantly faced with situations that require basic calculations. The key to mastering these challenges lies in a solid understanding of fundamental concepts and effective problem-solving techniques.
Practical exercises allow learners to grasp these concepts, providing real-life scenarios to work through. Whether it’s calculating discounts, managing income, or working out loan terms, having clear methods for approaching these problems is essential. The ability to break down complex tasks into manageable steps makes all the difference in applying these skills confidently.
Mastering these skills equips individuals with the tools necessary to handle personal finances, making informed decisions, and understanding the value of their money in everyday situations. Through dedicated practice and understanding, anyone can improve their ability to handle the numbers they encounter each day.
Practical Solutions for Everyday Calculations
Understanding and solving everyday numerical problems is essential for making informed decisions in financial matters. The ability to perform accurate calculations for tasks such as budgeting, pricing, and investments directly impacts how individuals manage their personal finances. This section offers a comprehensive approach to these types of problems, helping individuals navigate through various scenarios with confidence.
Breaking Down Financial Challenges
Financial challenges often involve determining amounts based on percentages, rates, and other variables. Learning how to calculate tax, discounts, or loan payments can be intimidating at first, but with clear methods and step-by-step guidance, these problems become much more manageable. Having reliable techniques for solving these types of issues helps make informed decisions on a daily basis.
Practical Examples and Techniques
Working through practical examples is one of the best ways to grasp concepts and understand their applications. Real-life situations, such as calculating savings from a sale or figuring out the total cost of an item with interest, provide valuable insight into how these skills are used in the real world. By regularly practicing these exercises, anyone can improve their ability to tackle similar challenges quickly and accurately.
Key Concepts in Consumer Mathematics
Understanding essential principles related to personal finance and daily transactions is crucial for managing money effectively. These foundational ideas help individuals make informed choices regarding budgeting, saving, spending, and investing. The ability to interpret various financial situations and apply practical solutions can significantly improve one’s financial stability.
Budgeting and Expense Management
One of the most important skills is the ability to create and follow a budget. This includes tracking income and outflows to ensure that spending stays within a reasonable limit. Effective management of regular expenses is key to maintaining financial health and avoiding debt accumulation.
Interest Rates and Loans
Understanding how interest rates impact loans and savings is vital for making wise financial decisions. Whether it’s taking out a loan or choosing an investment, grasping the effects of both simple and compound interest allows individuals to plan for future growth and manage repayment schedules effectively.
Step-by-Step Problem Solving Techniques
Effective problem-solving requires breaking down complex situations into manageable steps. By following a structured approach, individuals can tackle challenges more efficiently, ensuring that no crucial detail is overlooked. Each step helps build a clearer understanding, leading to more accurate solutions and better decision-making.
Start by clearly identifying the problem and gathering relevant information. Next, break the issue into smaller, more specific parts, and determine the necessary steps to address each one. Afterward, evaluate possible solutions and choose the most appropriate course of action. Finally, review the outcome to ensure the solution is effective and adjust if necessary.
How to Approach Word Problems
When faced with verbal problems, it’s essential to carefully analyze the given information and determine how to translate it into a solvable situation. Breaking down the problem step by step helps clarify the objectives and select the right method for reaching a solution. Staying organized and methodical ensures better accuracy and understanding.
Understanding the Key Information
The first step is to identify the crucial data presented in the problem. Often, this includes numbers, relationships, and specific conditions that guide the approach. Writing down the known facts can help clarify the next steps.
Setting Up the Solution
Once the necessary information is gathered, the next step is to determine the approach. This involves selecting the correct operation, creating equations, or visualizing the scenario. Below is a table summarizing the typical steps to follow:
| Step | Action |
|---|---|
| 1 | Read the problem carefully and highlight key information. |
| 2 | Translate words into numbers or symbols, if applicable. |
| 3 | Choose the appropriate method to solve the problem (e.g., addition, multiplication). |
| 4 | Perform calculations and check the results for accuracy. |
| 5 | Review the problem and ensure the solution makes sense. |
Tips for Mastering Budgeting Exercises
Budgeting exercises require careful planning, organization, and attention to detail. Whether you are tracking personal finances or simulating various spending scenarios, mastering these tasks can significantly improve your financial management skills. With a structured approach and a clear understanding of your goals, these exercises can become a valuable tool in everyday decision-making.
Start with a Clear Financial Overview
Before diving into budgeting tasks, it’s important to have a clear picture of your current financial situation. This includes understanding your income, expenses, and savings. By identifying the major categories of your finances, you can allocate your resources more effectively.
- List all sources of income.
- Track monthly expenses and categorize them (e.g., housing, groceries, entertainment).
- Set aside funds for emergency savings and long-term goals.
Utilize Budgeting Tools and Methods
Various tools and techniques can help streamline the budgeting process. These methods offer different levels of complexity, so choosing the right one depends on your comfort and experience.
- Zero-based budgeting: Allocate every dollar to a specific category.
- 50/30/20 rule: Spend 50% on needs, 30% on wants, and 20% on savings.
- Envelope system: Use cash for specific categories to control spending.
Utilizing Discounts and Markups Correctly
Understanding how to apply price reductions and increases is crucial for making informed financial decisions. These adjustments influence the final cost of goods or services, impacting both consumers and businesses. By grasping the methods behind these calculations, one can evaluate how such changes affect the overall budget and purchasing power.
Price reductions, often used in sales promotions, allow customers to purchase items at a lower cost. However, it is important to distinguish between a percentage off and a fixed amount off, as they have different effects on the final price. Conversely, markups, applied by sellers, ensure a profit margin on the cost price. Knowing how to calculate the right markup is essential for businesses to remain competitive while maintaining profitability.
Exploring Consumer Pricing Strategies
Effective pricing strategies are essential for businesses to attract customers while maintaining profitability. Various methods allow companies to balance competitive pricing with revenue goals, influencing purchasing decisions and market positioning. Understanding these techniques can help both sellers and buyers navigate the complexities of pricing structures in different industries.
- Penetration Pricing: This strategy involves setting a low initial price to attract customers and gain market share quickly, then gradually increasing the price once a customer base is established.
- Skimming Pricing: High initial prices are set for new or unique products, targeting consumers willing to pay a premium for early access or exclusivity.
- Psychological Pricing: Using pricing tactics that appeal to consumers’ emotional responses, such as pricing an item at $9.99 instead of $10 to create a perception of a bargain.
- Value-Based Pricing: This method sets prices based on the perceived value of a product or service to the customer rather than the cost of production.
- Discount Pricing: Offering periodic discounts or promotional deals to incentivize purchases, often used to clear inventory or boost sales during slow periods.
By leveraging these strategies, businesses can tailor their pricing to target specific customer needs and maximize their competitive advantage. Each approach offers unique benefits depending on the product, market conditions, and business objectives.
Real-World Applications of Math Skills
Mathematical abilities are fundamental in everyday life and play a key role in various fields. From managing finances to solving complex problems in professional settings, these skills are essential for making informed decisions and achieving practical outcomes. Understanding how to apply numerical reasoning can lead to better efficiency, accuracy, and success in numerous tasks.
Personal Finance and Budgeting
One of the most common areas where numerical skills are applied is personal finance. Whether it’s creating a budget, calculating savings growth, or planning for future expenses, the ability to manage numbers effectively is critical. Techniques such as determining interest rates, understanding loans, and tracking spending all require a strong grasp of basic calculations and budgeting principles.
Professional and Technical Fields
In technical and scientific fields, advanced numerical skills are indispensable. Engineers, architects, and data analysts rely on mathematical models and statistical analysis to design structures, optimize processes, and interpret data. By applying these skills, professionals can ensure precision, solve problems, and innovate within their respective industries.
How to Interpret Tax Calculations
Understanding how taxes are calculated is essential for managing personal finances and ensuring compliance with local regulations. Tax calculations involve determining the amount owed based on various factors such as income, deductions, and applicable tax rates. By breaking down the components of tax assessments, individuals can better understand how much they owe and why.
| Income | Tax Rate | Tax Owed |
|---|---|---|
| $50,000 | 15% | $7,500 |
| $80,000 | 20% | $16,000 |
| $120,000 | 25% | $30,000 |
The table above demonstrates a basic tax calculation based on income and tax rates. As income increases, the tax owed also increases proportionally, depending on the rate applied. Deductions and exemptions can further modify the final amount, but understanding the relationship between income and the corresponding tax rate is a key part of interpreting these calculations accurately.
Analyzing Investment Scenarios with Math
Evaluating potential returns on investments requires a solid understanding of numerical analysis. By calculating different variables such as interest rates, growth potential, and risk factors, individuals can assess the viability of various investment options. This process helps make informed decisions about where to allocate funds, optimizing returns while minimizing losses.
- Simple Interest: This is a basic method of calculating earnings or costs over time, where the interest is applied only to the principal amount.
- Compound Interest: Unlike simple interest, compound interest is calculated on both the initial principal and the accumulated interest, leading to exponential growth over time.
- Risk Assessment: A key factor in investment analysis involves understanding the level of risk involved in each scenario, helping to balance potential rewards with possible losses.
- Diversification: Spreading investments across various assets can reduce risk by ensuring that poor performance in one area does not severely impact the overall portfolio.
By applying these principles, investors can calculate expected returns and make strategic decisions that align with their financial goals. Whether investing in stocks, bonds, or real estate, mathematical analysis offers a structured approach to understanding potential outcomes and managing investment portfolios efficiently.
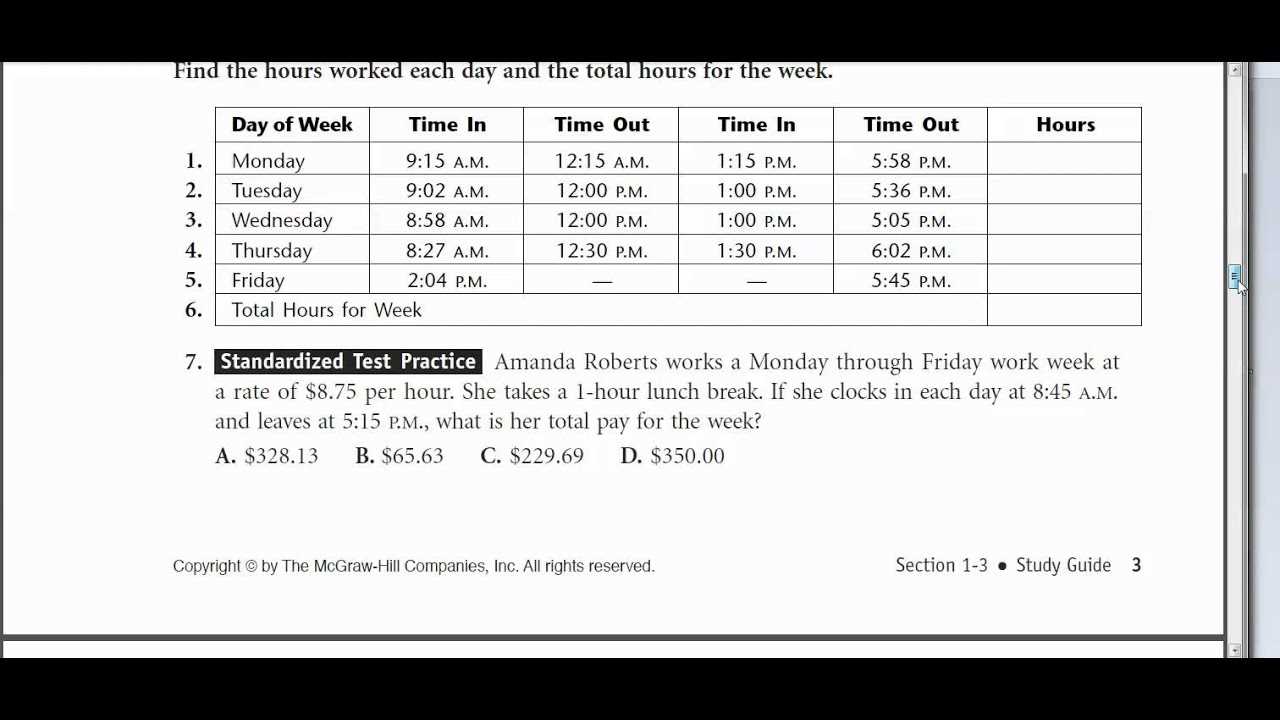
Working Through Payroll and Wages Problems
Calculating employee compensation involves understanding various factors that influence the final paycheck. These include hourly rates, overtime, deductions, and bonuses. By mastering these calculations, individuals and businesses can ensure accurate wage distribution and compliance with labor regulations. Having a systematic approach to payroll helps eliminate errors and promotes fairness in the workplace.
Hourly Wages Calculation: To determine earnings based on an hourly rate, multiply the number of hours worked by the hourly wage. For example, if an employee works 40 hours a week at $15 per hour, their gross pay would be $600.
Overtime Pay: Employees working beyond the standard hours are typically entitled to overtime compensation. Overtime pay is often calculated at a higher rate, usually 1.5 times the regular hourly rate. For instance, if the regular hourly wage is $15, the overtime rate would be $22.50 per hour.
Bonus and Commission Calculations: Bonuses or commissions are typically added to base wages. These amounts may depend on company performance, individual sales, or meeting specific targets. It’s important to factor these additional earnings into the total pay when calculating the employee’s final compensation.
By breaking down these components step by step, employers can manage payroll efficiently while ensuring their employees receive the correct wages. A clear understanding of these calculations supports transparent and accurate financial practices in any organization.
Effective Techniques for Estimations
Estimating is a vital skill in many situations, allowing individuals to make quick, approximate decisions without the need for precise calculations. Whether planning a budget, estimating time, or projecting costs, the ability to make reliable estimates can save time and resources. Several techniques can help enhance the accuracy and efficiency of these approximations.
Rounding Numbers for Simplicity
One of the most common techniques for making quick estimations is rounding numbers. By simplifying complex figures to the nearest ten, hundred, or thousand, calculations become more manageable. This method allows for faster mental math and is particularly useful when precise values are not necessary. For example, rounding $347 to $350 makes it easier to perform quick addition or subtraction.
Using Benchmarks and Reference Points
Another useful method is to rely on familiar benchmarks or reference points. These are known values or estimates that can serve as a guide for making approximations. For instance, estimating the cost of groceries by comparing prices to a known benchmark–such as the typical price for a similar item–can provide a rough but effective estimate without detailed analysis.
By combining these strategies, individuals can improve their ability to make accurate estimates in a variety of scenarios, from budgeting to planning and beyond. These techniques not only save time but also help in making more informed, confident decisions.
Solving Percentage-Based Problems
Percentage-based problems are common in everyday life, from calculating discounts to figuring out tax or interest rates. Understanding how to solve these problems efficiently helps make informed financial decisions and ensures accuracy. The key to solving such problems is knowing how to express a part of a whole as a percentage and how to work with this ratio in different contexts.
Basic Percentage Calculation
To calculate a percentage of a given number, use the formula:
- Percentage = (Part / Whole) × 100
For example, if you want to find 20% of $50, the calculation is:
- 20% of $50 = (20 / 100) × 50 = $10
Finding the Whole from a Percentage
Sometimes, it’s necessary to find the whole amount when you know the percentage and the part. In this case, rearrange the formula to:
- Whole = Part / (Percentage / 100)
For example, if you know that $30 is 25% of a total, to find the whole amount, calculate:
- Whole = 30 / (25 / 100) = $120
By applying these techniques, you can easily handle various percentage-based problems in real-world situations, from budgeting to pricing and beyond.
Common Mistakes and How to Avoid Them
When working with numbers and calculations, errors are often made that can lead to incorrect results. These mistakes can be small but significant, affecting decisions or outcomes. Understanding common pitfalls and knowing how to avoid them is crucial for accuracy and efficiency in calculations. Awareness of these errors can help individuals approach problems more confidently and minimize costly missteps.
| Common Mistake | How to Avoid It |
|---|---|
| Misplacing Decimal Points | Always double-check the placement of decimal points, especially when multiplying or dividing large numbers. |
| Incorrectly Applying Percentages | Remember that a percentage must be expressed as a fraction (e.g., 20% = 0.20) before performing calculations. |
| Forgetting to Account for Units | Be sure to include appropriate units in every calculation (e.g., dollars, pounds, liters) to avoid confusion or errors. |
| Overlooking Rounding Rules | Round numbers correctly based on the required precision, and avoid premature rounding before performing calculations. |
By being aware of these common mistakes, individuals can improve their ability to solve problems accurately. Taking extra care when performing calculations and reviewing the steps can lead to more reliable results and avoid costly errors in both everyday and professional scenarios.