
In this section, we explore effective methods for tackling complex mathematical problems. Whether you’re working through challenging exercises or aiming to improve your understanding, this guide provides clear paths to mastering the material. We focus on the techniques that can help clarify difficult concepts and strengthen your problem-solving skills.
Step-by-step explanations and carefully designed examples are key components of this approach, helping to simplify even the most complex topics. By breaking down each concept into manageable parts, you’ll gain the confidence to approach similar problems with ease. This guide aims to enhance both your knowledge and performance, making difficult topics more accessible and less intimidating.
Understanding Cpm Integrated Math 2 Answers
Grasping the key concepts and approaches to solving complex problems is essential in any learning process. When faced with challenging exercises, it’s important to break them down into simpler parts, ensuring that every step is understood. This section will guide you through a comprehensive process for achieving clarity and precision when tackling these types of problems, providing useful insights into the thought processes required to solve them effectively.
Step-by-Step Problem Solving Techniques
The key to mastering any subject is knowing the right techniques to approach problems. It starts with understanding the basic structure of each problem and identifying the tools you need to solve it. By following a systematic approach, you can simplify the process and ensure that you’re progressing logically toward the solution. Every problem has its own unique set of rules, and learning how to interpret these rules correctly is a fundamental skill in achieving success.
Improving Your Problem-Solving Skills

To strengthen your problem-solving ability, practice is crucial. Regularly working through different types of problems not only boosts your familiarity with the material but also enhances your ability to think critically. Analyzing past exercises and understanding where mistakes were made is a powerful way to learn. Each attempt contributes to developing a deeper understanding of the techniques and strategies needed for success.
Key Concepts in Integrated Math 2
Understanding the foundational principles behind mathematical problems is essential for mastering any subject. The key concepts covered in this section provide a framework for solving complex problems with confidence. By focusing on core ideas and techniques, learners can develop a deeper understanding of how different topics connect and how to apply them in a variety of scenarios.
Algebraic Structures and Functions
One of the core areas in this study involves exploring algebraic structures and their applications. Recognizing how different functions work and understanding their relationships is crucial for solving equations and analyzing problems. Key concepts include:
- Linear equations and inequalities
- Polynomial expressions
- Factoring techniques
- Systems of equations
By mastering these concepts, students can confidently approach more advanced topics and build a solid foundation for problem-solving.
Geometrical and Statistical Thinking
Alongside algebra, geometry and statistics form an essential part of this curriculum. These areas focus on understanding shapes, angles, and data analysis. Some important topics include:
- Geometric transformations and symmetry
- Area, volume, and surface area calculations
- Probability and data representation
- Statistical analysis and interpretation
Developing these skills allows learners to see the connections between abstract concepts and real-world applications, improving both their critical thinking and analytical abilities.
How to Approach Math 2 Problems
When faced with challenging problems, it’s important to have a clear strategy to guide your efforts. A structured approach not only helps in organizing thoughts but also improves the accuracy and efficiency of solving each task. Whether dealing with equations, shapes, or data analysis, understanding the underlying steps is essential for success.
Start by carefully reading the problem and identifying what is being asked. It’s crucial to take note of any given information and how it relates to the solution. Then, break down the problem into smaller, manageable parts. This allows you to tackle each element individually, minimizing the risk of overlooking important details.
Once the problem is dissected, focus on choosing the most effective method to solve it. Sometimes a direct formula or rule can be applied, while other times, a step-by-step reasoning process may be required. Always check your progress and results to ensure they make sense within the context of the problem.
Common Challenges in Cpm Math 2
Students often face various difficulties when dealing with complex problems. These challenges can stem from understanding concepts, applying formulas, or even interpreting the given information correctly. Recognizing these common issues allows learners to address them more effectively, ultimately improving their skills and confidence in solving problems.
Some of the most frequent difficulties encountered in this subject include:
| Challenge | Description |
|---|---|
| Pacing and Time Management | Many students struggle with completing problems in a timely manner, especially when the problems require multiple steps or detailed analysis. |
| Complex Problem Structures | Problems may have multiple components or require understanding of various principles, making them difficult to approach without a clear strategy. |
| Interpreting Word Problems | Word problems can be particularly challenging as they require translating real-world scenarios into mathematical terms. |
| Retention of Key Concepts | It can be difficult to retain the concepts and apply them correctly across different problems, especially when they build upon previous lessons. |
By identifying these obstacles, students can focus on improving specific areas and develop strategies to overcome them, leading to better outcomes and a stronger understanding of the material.
Step-by-Step Guide to Math 2 Solutions
Solving complex problems requires a clear and organized approach. By following a structured process, you can break down each task into manageable steps. This guide provides a systematic method for tackling difficult exercises, helping you to navigate through problems with confidence and precision.
Understanding the Problem

The first step in solving any problem is to fully comprehend the task at hand. Carefully read through the problem and identify the key information provided. Look for essential data such as values, variables, and relationships between elements. Understanding the underlying question is crucial before proceeding with any calculations or reasoning.
Breaking Down the Solution
Once you have a clear understanding of the problem, divide the task into smaller steps. This makes the problem less overwhelming and ensures that you address every part of the question. Approach each step logically, applying the relevant concepts and methods as needed. Remember to check your work regularly to ensure you’re moving in the right direction and haven’t missed any crucial details.
By following this step-by-step method, you can confidently approach even the most challenging exercises, improving your problem-solving skills and achieving better results.
Essential Resources for Math 2 Success
Achieving success in this subject requires access to a variety of resources that can enhance your understanding and problem-solving abilities. From textbooks and online platforms to practice exercises and study groups, the right tools can make a significant difference in mastering the material. Identifying and utilizing these resources is key to improving your performance and grasp of the concepts.
Textbooks and Study Guides
Textbooks remain one of the most reliable resources for gaining a thorough understanding of fundamental concepts. They provide structured content, clear examples, and detailed explanations of key topics. Study guides can be helpful as well, offering concise summaries, additional practice problems, and tips for exam preparation. Both tools are essential for reinforcing what you’ve learned and ensuring you’re well-prepared for tests.
Online Learning Platforms
Online platforms and video tutorials can offer dynamic explanations of complex topics. Websites dedicated to educational resources provide interactive lessons, step-by-step solutions, and discussion forums where students can ask questions and collaborate. These platforms often offer free or affordable resources, making them easily accessible for anyone looking to improve their skills.
By integrating these essential tools into your study routine, you can approach each topic with confidence and continue building the necessary skills for success in this course.
Breaking Down Complex Math 2 Problems
When faced with a difficult problem, the key to success lies in simplifying the task. Breaking down a complex problem into smaller, more manageable parts helps to reduce confusion and increase clarity. By carefully analyzing each component of the problem, you can approach it step by step, ensuring no detail is overlooked.
Here is a guide to help you effectively tackle challenging problems:
- Read the Problem Carefully: Begin by thoroughly reading the problem to identify key information such as numbers, variables, and relationships. Understanding the context is crucial before starting any calculations.
- Highlight Important Data: Underline or note down the critical values, conditions, and any information that directly affects your solution process.
- Divide the Problem: Break the problem into smaller parts, focusing on one section at a time. This helps to reduce the complexity and makes the problem easier to solve.
- Apply Relevant Concepts: Use the appropriate formulas or techniques related to each part of the problem. Avoid skipping any steps, even if they seem straightforward.
- Check Your Work: After solving, review each step to ensure there are no mistakes. Checking your work ensures accuracy and helps identify any errors in the process.
By following this structured approach, you can approach even the most complex problems with confidence, breaking them down into smaller tasks and solving them efficiently.
Tips for Efficient Problem Solving
Effective problem-solving is a skill that can be honed through practice and the application of certain strategies. By approaching problems with a structured mindset and following key techniques, you can solve problems faster and more accurately. Implementing these tips can help streamline the process and improve your overall efficiency.
Here are some essential tips for tackling problems more effectively:
| Tip | Description |
|---|---|
| Understand the Problem | Before jumping into solving, take time to fully comprehend the problem. Identify the key details and what is being asked. |
| Break It Down | Divide the problem into smaller, more manageable steps. This helps prevent feeling overwhelmed and allows for a more systematic approach. |
| Use Visual Aids | Whenever possible, draw diagrams or charts. Visual representations can make complex information easier to understand and manipulate. |
| Work Methodically | Follow a step-by-step process and ensure each part is completed before moving on. This ensures accuracy and prevents mistakes. |
| Review Your Work | Always double-check your solution. Reviewing ensures you haven’t made any errors and confirms that your solution is correct. |
By applying these strategies, you can enhance your problem-solving skills and tackle challenges with greater confidence and efficiency.
Exploring Cpm Math 2 Curriculum
The curriculum designed for this level offers a comprehensive approach to learning that emphasizes conceptual understanding and real-world applications. It is structured to guide students through complex topics by encouraging exploration and critical thinking. Throughout the course, learners engage with diverse methods of problem-solving, fostering a deeper grasp of the subject matter.
This approach not only strengthens foundational knowledge but also develops the skills necessary for tackling increasingly challenging tasks. The curriculum is divided into units that build on each other, allowing for a progressive learning experience. Each unit introduces new concepts while reinforcing previous lessons, ensuring that students gain mastery step by step.
Key features of this curriculum include hands-on activities, collaborative work, and an emphasis on reasoning and communication. Students are encouraged to approach problems from multiple angles, enhancing their ability to think critically and creatively. The course material is designed to be accessible, with clear explanations and examples that support the learning process at every stage.
Mastering Algebra in Math 2
Algebra plays a pivotal role in building strong problem-solving skills and is a cornerstone of advanced learning. At this level, students focus on developing a deep understanding of algebraic expressions, equations, and functions. By mastering these concepts, learners are equipped to approach increasingly complex problems with confidence and precision.
The study of algebra involves understanding the relationships between variables and constants. It helps students gain the ability to manipulate expressions, solve equations, and apply algebraic techniques to real-world scenarios. Mastery in this area is achieved by practicing problem-solving strategies, analyzing patterns, and gaining familiarity with different types of equations and their solutions.
Understanding Variables and Expressions
A critical component of algebra is learning how to work with variables and expressions. Variables represent unknown quantities, and expressions are combinations of numbers, variables, and operations. Through practice, students develop the ability to simplify, expand, and factor expressions, making it easier to solve complex equations.
Solving Equations and Inequalities
Solving equations and inequalities is a fundamental skill in algebra. Students learn how to isolate variables, apply operations to both sides of an equation, and understand the meaning of solutions. Inequalities, which express relationships between quantities that are not equal, are also explored, with an emphasis on graphing solutions on number lines and coordinate planes.
Geometry Principles in Math 2
Understanding the foundational concepts of geometry is essential for developing critical thinking and problem-solving skills. This area of study explores the properties and relationships of shapes, sizes, and spaces. Through these principles, students can approach complex spatial problems and apply their knowledge in various real-world contexts, such as architecture and design.
At this level, the focus is on both two-dimensional and three-dimensional figures. Students are introduced to key concepts such as angles, lines, and polygons, as well as the relationships between them. By grasping these principles, learners gain the ability to calculate areas, volumes, and other essential measurements critical to geometry.
Angles and Their Properties
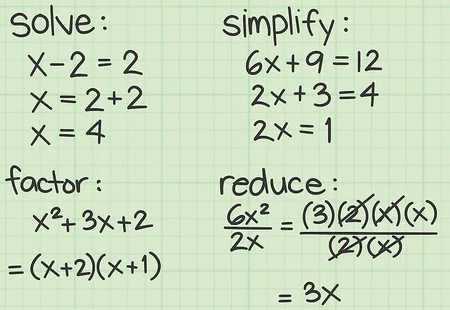
Angles are a fundamental aspect of geometry. Students begin by learning how to measure and classify angles, understanding the relationships between different types, such as acute, obtuse, and right angles. They also explore angle pairs like complementary and supplementary angles, which play a significant role in solving geometric problems.
Properties of Shapes and Figures

In geometry, a deep understanding of the properties of various shapes is essential. Students explore the characteristics of triangles, quadrilaterals, circles, and other polygons. They learn to calculate the perimeter and area of these shapes, as well as apply theorems, such as the Pythagorean theorem, to solve real-world and theoretical problems.
Real-World Applications of Math 2
The concepts learned in advanced problem-solving courses are not only theoretical but have a wide range of practical applications in everyday life. Understanding these principles allows individuals to approach real-world challenges in fields like engineering, finance, architecture, and even in technology. By using the knowledge of shapes, measurements, and problem-solving techniques, students can effectively navigate complex situations and make informed decisions in various industries.
One of the key aspects of applying these principles is in solving real-world problems related to design, construction, and budgeting. Whether it’s calculating the area of a space for construction, determining optimal solutions for resource allocation, or even designing digital systems, the skills developed in these areas provide valuable tools for professionals across many fields.
Applications in Construction and Design
In the fields of architecture and engineering, geometric principles are used extensively to design structures, calculate material requirements, and ensure safety. For example, the calculation of areas, volumes, and angles helps architects determine the optimal dimensions for buildings and other infrastructure.
Applications in Finance and Economics
In finance, advanced techniques such as modeling financial data, calculating rates of return, and understanding probability all rely on problem-solving skills. These methods are used to make predictions, assess risks, and determine the viability of investment opportunities.
| Field | Application | Example |
|---|---|---|
| Engineering | Structural design and optimization | Calculating the load-bearing capacity of a bridge |
| Architecture | Designing floor plans and layouts | Determining the dimensions of a room |
| Finance | Investment analysis and risk assessment | Evaluating a stock’s potential return |
How to Check Your Answers
Verifying the correctness of your solutions is an essential step in problem-solving. Whether you’re working on numerical challenges or conceptual problems, ensuring that your approach is accurate helps build confidence in your abilities. The process of double-checking involves reviewing the steps taken and confirming that each one aligns with the expected results, ensuring a thorough understanding of the problem.
Review Your Steps
Start by retracing your work and verifying that every calculation was done correctly. Check for common mistakes such as misplacing a decimal point, adding or subtracting incorrectly, or skipping a necessary step. By carefully going over each stage of the process, you can identify where things might have gone wrong and make the necessary corrections.
Use Alternate Methods
Another effective way to verify your solution is by using a different approach to solve the same problem. This could include using a different formula, method, or strategy that may offer a fresh perspective. If the alternate solution agrees with your initial result, it’s likely that your answer is correct. This technique is particularly useful when tackling complex problems that involve multiple steps or variables.
Understanding Word Problems in Math 2
Word problems often appear complex at first, but they are simply real-world scenarios that require logical thinking and systematic steps to solve. These types of questions test your ability to translate a situation into mathematical operations and find a solution. The key to tackling word problems is breaking them down into manageable parts, identifying the relevant information, and selecting the correct approach to solve them.
When faced with a word problem, it’s crucial to follow a clear process to ensure you don’t miss any important details. Start by carefully reading the entire problem and underlining or highlighting the essential data. Then, identify what is being asked and what mathematical operations are needed to find the solution.
Steps to Solve Word Problems
- Read the problem carefully: Understand the context and what is being asked.
- Identify key information: Look for numbers, units, and relationships that are crucial to the solution.
- Choose the correct operation: Decide whether to add, subtract, multiply, or divide based on the problem’s requirements.
- Set up an equation: Write out the equation or expression based on the information provided.
- Solve the equation: Perform the necessary calculations to find the result.
- Check your answer: Review the problem to ensure the solution makes sense in the context of the situation.
Common Mistakes to Avoid

- Misunderstanding the question: Be sure to read the problem in full before attempting to solve it.
- Forgetting units: Always include and check the units in your final answer to ensure consistency with the problem.
- Skipping steps: Don’t rush through the problem. Break it down step by step to avoid errors.
Utilizing Resources Effectively
In any learning process, having access to quality materials can significantly enhance understanding and problem-solving abilities. The key is knowing how to use these resources to their fullest potential. Whether it’s textbooks, online platforms, or interactive guides, each tool offers unique ways to approach concepts and solidify comprehension. Understanding when and how to leverage these resources is crucial to mastering the material.
To get the most out of available resources, it’s important to identify which ones align with your learning style. Some learners benefit from visual aids, while others prefer textual explanations or hands-on practice. Integrating various types of resources can provide a well-rounded approach and make challenging topics more accessible.
One of the most effective ways to use resources is to first attempt problems on your own before seeking help. This helps identify gaps in understanding, which can be addressed by consulting the relevant materials. Additionally, taking advantage of online tools or study groups can provide additional perspectives that may make difficult concepts clearer.
Improving Test Scores in Math 2
Achieving higher results on tests requires a combination of effective study habits, consistent practice, and strategic preparation. By adopting a focused approach, students can enhance their understanding and performance. It’s not just about working harder, but working smarter, using the right methods to reinforce knowledge and build confidence.
Here are some strategies to improve your test scores:
- Review Key Concepts Regularly: Consistent revision helps solidify foundational principles and avoid last-minute cramming.
- Practice Problem-Solving: The more problems you solve, the more familiar you become with different question types and solutions.
- Take Timed Practice Tests: Simulating exam conditions can help manage time during the actual test and reduce anxiety.
- Seek Help When Needed: Don’t hesitate to ask for clarification on difficult concepts, whether from a teacher, tutor, or peer.
- Use Study Aids: Tools like flashcards, online resources, or instructional videos can provide a different perspective on challenging material.
Incorporating these strategies into your routine can significantly boost your ability to retain information and apply it effectively during tests.