Go Math 5th Grade Answers and Solutions

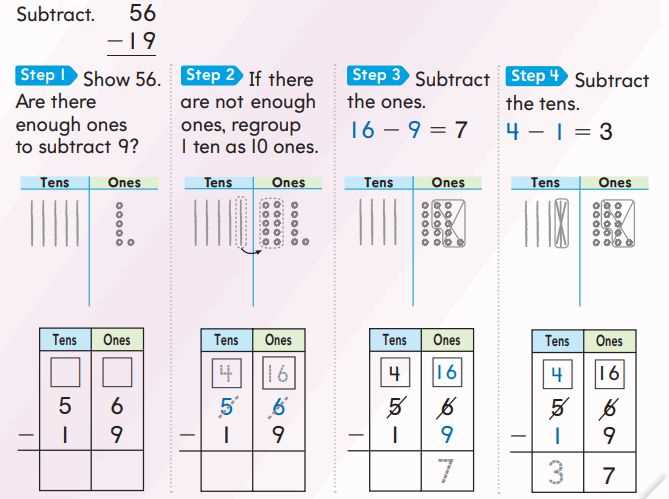
Mastering the key concepts of elementary-level numerical skills is essential for students to succeed in their educational journey. Whether it’s tackling complex word problems or understanding fundamental operations, having access to effective resources can make all the difference in learning.

Comprehending tricky problems requires more than just memorizing steps; it’s about building a deeper understanding of how numbers interact and how to approach them methodically. This guide provides detailed solutions for a wide range of exercises, focusing on strengthening skills and boosting confidence.

With clear explanations and step-by-step breakdowns, students can easily follow along and learn to solve problems independently, ensuring a solid foundation for more advanced topics in the future. Whether you’re looking for help with specific questions or general study tips, these solutions will guide the way forward.

Go Math 5th Grade Answers Overview

In this section, we will explore how to navigate the various problem-solving strategies and resources available for elementary-level learning. The goal is to provide clarity and assistance for students who are working through exercises that require a structured approach to solving numerical challenges.

Each problem set is designed to strengthen fundamental skills and help students build confidence. The solutions guide offers a comprehensive look at how to effectively approach different types of tasks, ensuring that learners can follow along with ease.

Key features of the guide include:

• Clear and concise step-by-step instructions for tackling problems.
• Effective strategies to handle complex questions and tricky situations.
• Practical tips for reinforcing concepts and improving retention.
• Structured exercises that build upon each other to promote gradual learning.

Whether it’s understanding basic operations or handling more involved calculations, these insights are tailored to support each student’s learning path. By focusing on these strategies, learners can approach their studies with greater confidence and achieve better results in their assessments.

How to Approach Go Math Problems

Solving complex numerical tasks requires a strategic approach that helps break down problems into manageable parts. By understanding the structure of each question and applying a systematic method, students can tackle even the most challenging exercises with confidence.

Start by carefully reading each problem to ensure that all the given information is understood. Pay attention to key details such as the numbers involved, the operations required, and any special instructions. Once the problem is fully grasped, it becomes easier to identify the steps needed to find the solution.

Effective problem-solving often involves the following steps:

• Identify the type of task (addition, subtraction, multiplication, division, etc.).
• Organize the information in a clear and logical manner.
• Break the problem down into smaller, simpler steps.
• Double-check the calculations and ensure that each step is correct.
• Review the final solution to verify its accuracy.

By applying this approach consistently, students can develop strong problem-solving skills and improve their ability to handle various types of questions. These strategies not only assist in completing exercises but also build a foundation for more advanced topics in future studies.

Understanding Go Math Answer Keys

Answer keys serve as essential tools for guiding students through the problem-solving process. They not only provide the correct results but also offer insight into the logical steps that lead to those results. Understanding how to use these resources effectively can greatly enhance a student’s ability to approach problems with confidence and precision.

How Answer Keys Help in Learning

When working through exercises, answer keys offer a roadmap for verifying calculations and understanding the methods used to solve problems. By reviewing the steps provided, students can identify patterns, strategies, and techniques that they may have missed or overlooked while attempting the problems themselves. This process of comparison fosters deeper learning and encourages self-correction.

Using Answer Keys for Skill Development

While answer keys can be helpful for checking work, it’s important not to rely solely on them. The true value lies in using them as a tool for practice and self-improvement. By carefully examining the solutions, students can reinforce their understanding of mathematical concepts, allowing them to apply these skills more effectively in future tasks. Consistent practice, coupled with the guidance of answer keys, leads to greater mastery and problem-solving efficiency.

Step-by-Step Guide to Go Math Solutions

Breaking down complex problems into manageable steps is key to solving them efficiently and accurately. By following a clear and structured approach, students can navigate through any exercise and develop a better understanding of the process behind each solution.

Step 1: Read the Problem Carefully

Before attempting any calculations, carefully read through the entire problem. Make sure to understand what is being asked and identify the essential information. Look for clues about the operations required, such as addition, subtraction, or multiplication, and note any specific instructions.

Step 2: Organize the Information

Write down the key numbers, variables, and facts from the problem. Organizing the information visually can make it easier to see the relationships between different elements. If the problem involves multiple steps, consider creating a simple chart or list to keep track of the data.

Step 3: Plan the Solution

Determine the appropriate method or strategy to solve the problem. This may involve choosing the correct operation or breaking the problem into smaller parts. Planning ahead ensures that each step is focused and purposeful.

Step 4: Execute the Plan

Carefully perform the necessary calculations. Double-check each step as you go to avoid mistakes. If the problem involves more than one operation, make sure to follow the correct order of operations to reach an accurate result.

Step 5: Review and Verify

Once the solution has been reached, take a moment to review the steps and verify the final result. This helps ensure that no errors were made during the process. If necessary, rework the problem to confirm the answer.

By following these steps consistently, students can approach problems with confidence and improve their problem-solving skills. The more practice they get, the more efficient they will become at tackling any numerical challenge that comes their way.

Top Tips for 5th Grade Math Success

Achieving success in numerical exercises requires a combination of focus, practice, and effective strategies. By following certain tips and techniques, students can enhance their understanding and performance, making it easier to tackle a variety of challenges and build confidence along the way.

1. Build a Strong Foundation

Before diving into more complex problems, it’s essential to have a solid grasp of the basic concepts. Reinforce your understanding of simple operations, such as addition, subtraction, multiplication, and division. These skills are the building blocks for solving more difficult tasks and will make future lessons much easier to comprehend.

2. Develop Problem-Solving Strategies

Having a systematic approach to problem-solving can make even the most challenging questions more manageable. Consider these tips:

• Read each problem carefully to fully understand what’s being asked.
• Organize your information in a clear and logical way.
• Break complex problems into smaller, more manageable parts.
• Double-check your work and ensure each step is accurate.

3. Practice Regularly

Consistent practice is key to improving skills. Set aside time each day to work on numerical tasks, and aim to cover a variety of topics. The more problems you solve, the more familiar you will become with different types of questions and the better prepared you will be for future assessments.

4. Seek Help When Needed

If you’re struggling with a particular concept or problem type, don’t hesitate to ask for help. Whether it’s a teacher, tutor, or classmate, getting clarification can prevent misunderstandings and provide valuable insights that will make the learning process smoother.

By following these strategies and focusing on regular practice, students can build the skills they need to succeed in their studies and feel confident when approaching new challenges. Persistence and the right mindset are essential for achieving long-term success.

Common Challenges in Go Math Worksheets

When working through numerical exercises, students often encounter various difficulties that can hinder their progress. These challenges may arise from misunderstanding the problem, misapplying a concept, or struggling with the complexity of certain tasks. Identifying and addressing these obstacles can help learners build the confidence they need to improve their skills and performance.

Here are some common challenges students face:

Challenge	Description
Word Problems	Interpreting the language and extracting the necessary information can be difficult for many students, making it hard to identify the correct operation to use.
Multiple-Step Problems	Problems that require several steps to solve can be overwhelming, leading to confusion or errors if each step is not approached systematically.
Fractions and Decimals	Understanding how to convert between fractions, decimals, and percentages often presents challenges, as students may struggle with the relationships between these forms.
Time Management	Students may struggle with managing time when faced with long worksheets or assignments, leading to rushed answers or incomplete tasks.
Application of Concepts	Applying theoretical knowledge to practical problems can be difficult, especially when students are unfamiliar with the problem types or haven’t practiced them enough.

By recognizing these challenges, students can take proactive steps to improve their understanding and approach. Seeking additional practice, reviewing concepts that are causing confusion, and staying organized are key strategies to overcoming these common difficulties.

How to Use Go Math Effectively

Maximizing the benefits of educational resources requires a thoughtful and strategic approach. When working through exercises, it is important to focus not just on finding the right answer, but also on understanding the process behind it. By using these tools wisely, students can strengthen their problem-solving skills and develop a deeper understanding of key concepts.

To make the most out of these resources, consider the following tips:

• Work Consistently: Set aside regular time for practicing exercises to build familiarity with different problem types and reinforce concepts.
• Review Step-by-Step: Pay close attention to each solution and ensure you understand every step before moving on to the next one. This reinforces learning and helps retain information.
• Break Down Complex Problems: If you encounter a challenging task, break it into smaller, more manageable steps. This makes the problem less overwhelming and ensures you don’t miss any key components.
• Seek Clarification: When stuck, don’t hesitate to ask for help from a teacher, tutor, or peer. Understanding the reasoning behind each solution can clarify difficult concepts.
• Use Practice Resources: Beyond the worksheets, use additional online tools or study guides to further reinforce your understanding of specific topics.

By following these strategies, students can make the most of their resources, improving both their skills and their confidence when tackling future challenges. The goal is to create a deeper understanding that goes beyond simply finding the correct result, but rather mastering the problem-solving process itself.

Strategies for Solving Word Problems

Word problems often present a unique challenge because they require students to translate written information into mathematical operations. The key to solving these types of problems effectively lies in breaking them down into manageable steps and identifying the important details. By following a systematic approach, students can tackle even the most complex problems with confidence.

1. Understand the Problem

The first step in solving any word problem is to carefully read through the entire question. Pay attention to the specifics, such as what is being asked and which information is given. Highlighting or underlining key words, like “total,” “difference,” or “how much,” can help identify the required operations. Take time to fully understand the context before proceeding to the next step.

2. Identify and Organize Information

Once the problem is understood, the next step is to organize the given information. This can be done by writing down important numbers or creating a visual aid, such as a chart or diagram. Breaking down the information into smaller pieces makes it easier to see the relationships between different elements and figure out what needs to be done.

For example, if a problem involves multiple quantities, list them out and clearly label each one. This will help keep everything organized and prevent missing any critical details.

3. Choose the Right Operation

After organizing the information, determine which mathematical operation is needed. Look for clues in the question–words like “add,” “subtract,” “multiply,” or “divide” usually indicate the operation. In more complex problems, there may be multiple steps involved, so ensure you understand the order in which they should be performed.

4. Solve and Check Your Work

Once the correct operation is chosen, solve the problem step by step. Always double-check your work as you go along. If the answer seems incorrect or too large/small, go back and review your steps. Verifying your solution by re-reading the question and checking that all information has been used correctly is essential for ensuring accuracy.

By following these strategies, students can approach word problems with greater ease and clarity, improving both their problem-solving skills and their confidence in handling complex questions.

Understanding Fractions in Go Math

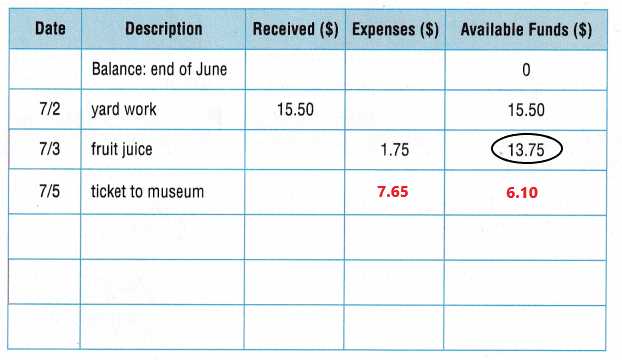
Working with fractions is an essential skill in solving many numerical problems. Fractions represent parts of a whole and are crucial for understanding how quantities are divided. In order to solve problems involving fractions effectively, it’s important to have a clear understanding of their components and how to manipulate them.

Here are key points to keep in mind when working with fractions:

• Numerator and Denominator: A fraction consists of two parts–the numerator (top number) represents how many parts are being considered, while the denominator (bottom number) shows how many equal parts the whole is divided into.
• Equivalent Fractions: Fractions that may look different but represent the same value. For example, 1/2 is equivalent to 2/4. Recognizing equivalent fractions is important for simplifying and comparing fractions.
• Adding and Subtracting Fractions: To add or subtract fractions, the denominators must be the same. If they are different, you will need to find a common denominator before performing the operation.
• Multiplying Fractions: When multiplying fractions, simply multiply the numerators and the denominators separately. For example, 2/3 × 4/5 = 8/15.
• Dividing Fractions: To divide fractions, multiply the first fraction by the reciprocal (flipped version) of the second fraction. For example, 2/3 ÷ 4/5 = 2/3 × 5/4 = 10/12, which simplifies to 5/6.

By mastering these basic concepts, students will be able to tackle fraction-related problems with confidence and accuracy. Practicing these skills regularly will improve both speed and understanding, making complex tasks much more manageable.

Mastering Decimals and Percentages

Decimals and percentages are two essential concepts that students need to understand in order to tackle a wide range of numerical problems. While decimals represent parts of a whole in a base-10 system, percentages offer a way to express these parts as a fraction of 100. Mastering both allows students to approach problems in various contexts with greater confidence and precision.

Understanding Decimals

Decimals are a way of expressing numbers that are not whole by using a decimal point to separate the whole number part from the fractional part. Each digit after the decimal point represents a fraction of 10, 100, 1000, and so on. Converting between fractions and decimals is a critical skill that helps students navigate a variety of problems.

• Converting Fractions to Decimals: To convert a fraction to a decimal, divide the numerator by the denominator. For example, 3/4 becomes 0.75.
• Adding and Subtracting Decimals: When adding or subtracting decimals, ensure that the decimal points align. Perform the operation as you would with whole numbers, and place the decimal point in the correct position in the result.
• Multiplying and Dividing Decimals: When multiplying or dividing decimals, treat them as whole numbers first, then adjust the decimal point in the final answer based on the number of decimal places in the factors.

Understanding Percentages

Percentages are another way to represent fractions, where the denominator is always 100. They are particularly useful in situations involving comparisons or when calculating discounts, interest rates, or proportions. Understanding how to convert between fractions, decimals, and percentages is vital for solving real-life problems.

• Converting Decimals to Percentages: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 becomes 75%.
• Finding the Percentage of a Number: To calculate a percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, 25% of 200 is 200 × 0.25 = 50.
• Converting Percentages to Fractions: To convert a percentage to a fraction, write the percentage as a fraction over 100 and simplify if possible. For example, 40% becomes 40/100, which simplifies to 2/5.

By mastering decimals and percentages, students can effectively handle a variety of problems, from basic calculations to more complex applications in everyday situations. Regular practice with these concepts will help reinforce their understanding and make them more comfortable working with numbers in different forms.

Go Math Geometry and Measurement Tips

Geometry and measurement are key areas of study that help students understand the properties of shapes, sizes, and spatial relationships. Whether dealing with simple shapes or more complex figures, mastering these concepts is essential for solving problems and applying mathematical reasoning to real-world situations. In this section, we will explore useful tips and strategies for tackling problems in geometry and measurement.

When working with geometric shapes, it is important to recognize their properties, such as the number of sides, angles, and symmetry. Measurement skills, on the other hand, require an understanding of different units and how to convert between them, as well as how to calculate areas, volumes, and perimeters accurately.

• Understanding Shape Properties: Start by identifying key features of different shapes, such as triangles, quadrilaterals, and circles. Learn to recognize how sides, angles, and symmetry relate to each other, which can help in solving problems related to perimeter and area.
• Perimeter and Area: To calculate the perimeter of a shape, add the lengths of all its sides. For area, use the appropriate formula, such as length × width for rectangles or π × r² for circles. Practice applying these formulas to various shapes to improve accuracy.
• Working with Angles: Understanding different types of angles–acute, obtuse, right–can help when working with triangles and other polygons. Use a protractor to measure angles and apply angle sum properties in polygons to solve problems.
• Volume and Surface Area: For three-dimensional figures, such as cubes or spheres, it’s important to use the correct formulas to calculate volume and surface area. For a rectangular prism, for example, use the formula length × width × height to find the volume.
• Units of Measurement: Be familiar with different units of length, area, and volume. Understand how to convert between units (e.g., from centimeters to meters or square inches to square feet) to ensure the correct answers when solving problems.

Mastering geometry and measurement is essential not only for academic success but also for real-world problem-solving. Regular practice with different types of shapes, measurements, and calculations will help students gain the confidence to approach these topics with ease and accuracy.

Reviewing Go Math Practice Tests

Practice tests are an excellent tool for reinforcing knowledge and evaluating understanding. By regularly reviewing practice tests, students can identify areas of strength and areas that may require further attention. These assessments provide a structured way to measure progress, reinforce concepts, and build confidence before tackling more complex problems.

One of the key benefits of practice tests is that they simulate the type of questions students will face during assessments, allowing them to become familiar with the format and types of problems. In this section, we will explore effective strategies for reviewing practice tests and making the most of this valuable resource.

How to Analyze Practice Test Results

After completing a practice test, it’s important to take time to carefully review the results. Look beyond the correct and incorrect answers to understand why a particular answer was right or wrong. This process helps students gain deeper insight into their thought processes and identify areas where they may need to improve.

• Identify Mistakes: Focus on the mistakes made during the test and understand the reasoning behind them. Were the errors due to simple miscalculations, misunderstandings of concepts, or not following the correct procedure?
• Review Correct Answers: For correct answers, verify the steps taken to reach the solution. Were they done efficiently, or is there a faster, more accurate method to solve the problem?
• Note Patterns: Over time, certain patterns may emerge in mistakes, such as consistently misinterpreting certain types of questions. Recognizing these patterns will help target specific areas for improvement.

Maximizing the Learning from Practice Tests

While it’s important to review practice test results, it’s equally important to use the test as a learning tool. Here are some strategies to make the most out of practice test reviews:

• Rework Incorrect Problems: After identifying the mistakes, attempt to solve the problems again, but this time with a clearer understanding of the concepts. Reworking problems reinforces learning and helps solidify concepts.
• Seek Help for Unclear Concepts: If a certain concept or problem type continues to be challenging, don’t hesitate to ask for help. Whether from a teacher, a tutor, or a peer, getting clarification can provide the support needed to move forward.
• Use Additional Resources: If needed, supplement practice test reviews with additional exercises, videos, or practice questions to further reinforce learning.

By regularly reviewing practice tests, students can build strong problem-solving skills, gain confidence, and improve their overall performance. This consistent review process ultimately leads to better understanding and mastery of the material.

Boosting Speed with Go Math Techniques

Improving problem-solving speed is crucial for success in any academic discipline. By utilizing efficient strategies, students can solve problems more quickly without sacrificing accuracy. In this section, we will explore practical techniques that help boost speed while solving problems, ensuring that students can complete tasks within the time limits and with greater confidence.

One effective way to increase speed is through practice and familiarity with the types of problems that appear in assessments. Mastering key concepts and procedures allows students to recognize patterns and apply solutions more rapidly. Additionally, developing a systematic approach to problem-solving can reduce hesitation and improve efficiency.

Mastering Mental Calculations

One of the quickest ways to solve problems is by mastering mental arithmetic. By practicing basic calculations, students can perform operations in their heads rather than relying on written work, saving valuable time. Here are some tips for mastering mental calculations:

• Practice multiplication tables: Memorizing multiplication tables helps students solve multiplication and division problems faster.
• Use estimation: Estimating answers before solving can help quickly identify reasonable solutions, especially for problems that require rounding or approximating values.
• Break down complex problems: Instead of attempting to solve a complex problem all at once, break it into smaller, easier steps to simplify the process.

Developing Efficient Strategies

Another important technique for speeding up problem-solving is using efficient strategies tailored to the type of problem being solved. Developing a set of steps that can be applied consistently across different questions can help save time. Below are some strategies to consider:

• Identify key information quickly: When approaching a problem, quickly identify the most relevant details to avoid getting caught up in unnecessary information.
• Work systematically: A consistent approach, whether it’s working left to right or using a step-by-step method, can reduce confusion and increase efficiency.
• Avoid overthinking: Trust in the preparation and practice that has gone into understanding the material. Overthinking a problem can waste time and lead to errors.

By incorporating these techniques into regular practice, students can develop both speed and accuracy, making them more efficient problem-solvers. Continuous practice, along with a strategic approach, can help students gain the confidence needed to tackle problems quickly and effectively.

How to Check Go Math Answers

Verifying the correctness of solutions is a crucial step in the learning process. Ensuring that each solution is accurate helps reinforce understanding and builds confidence in one’s skills. In this section, we will discuss effective methods for reviewing and checking your work to guarantee that the answers provided are correct and reliable.

One of the most important steps in verifying solutions is understanding the process behind each problem. When you fully comprehend the steps taken to arrive at a solution, it becomes easier to identify any potential mistakes. Always start by reviewing each step logically to ensure that no steps were skipped or misunderstood.

Revisit Key Concepts

Before diving into checking specific answers, it is essential to refresh your understanding of the key concepts involved. If you’re unsure about certain steps, taking a moment to review related rules or formulas can often reveal errors or reinforce the correct approach. Here are a few strategies to use:

• Review definitions and formulas: Ensure that all the formulas and principles applied during the problem-solving process are correct and relevant to the question.
• Break down complex problems: Reevaluate any complicated calculations or procedures by breaking them into smaller, manageable pieces to confirm that each part is correct.

Use Alternative Methods

Sometimes, using a different approach to solve the same problem can help verify the accuracy of your results. If possible, try alternative methods or reverse operations to check your answers. This might include using estimation, graphing, or performing the opposite operation to see if the original calculation holds up. Other techniques include:

• Estimate your results: Quickly estimate the expected answer and compare it to your solution. If the results are vastly different, review your steps.
• Check using a calculator: For complex calculations, use a calculator to double-check the final result.

Finally, always cross-check your work with any available resources, such as textbooks or digital tools, to see if your solutions align with established methods. Through consistent practice and careful review, you can improve your accuracy and ensure that each solution is correct and reliable.

Getting Help with Go Math Concepts

Understanding complex topics can be challenging, but there are numerous resources available to provide support. Whether you’re struggling with specific concepts or just looking to reinforce your understanding, seeking help can make a significant difference in your learning experience. In this section, we explore different ways to access support and gain a deeper understanding of the material.

Sometimes, the best way to grasp difficult concepts is by breaking them down with the help of others. Reaching out for assistance, whether from teachers, peers, or online resources, can provide fresh perspectives and alternative explanations that make the learning process easier to follow. Here are a few methods to consider:

Use Educational Websites and Videos

Online resources have become invaluable tools for learners of all ages. Numerous websites and educational videos offer explanations, tutorials, and interactive exercises on a variety of topics. These can be especially useful when you’re looking for alternative ways to approach a problem. Some popular resources include:

• Tutorial Websites: Websites like Khan Academy or similar educational platforms offer step-by-step guides and examples for various topics.
• YouTube Tutorials: Many educators post videos explaining challenging concepts in simple, understandable terms.
• Interactive Problem Solvers: Certain websites provide tools where you can input problems and receive immediate feedback on how to solve them.

Study Groups and Peer Support

Collaborating with classmates or peers can also be an excellent way to reinforce your understanding. Group discussions allow for the sharing of ideas and strategies that can help clarify confusing points. Participating in study groups can help you:

• Gain different perspectives: Explaining concepts to others or hearing them explained in a new way can lead to a better understanding.
• Work through difficult problems together: Tackling challenges as a group allows for shared problem-solving and can highlight different strategies.

Additionally, don’t hesitate to ask your teacher for clarification. Teachers are there to help, and often providing specific examples or one-on-one time can make a big difference in how well you understand the material. If in-person help isn’t possible, consider reaching out via email or through a virtual platform for extra assistance.

By utilizing these resources and strategies, you can improve your grasp on challenging concepts and increase your confidence in solving problems independently.

Using Go Math for Test Preparation

Preparing for exams can often feel overwhelming, but using structured resources can make the process more manageable and effective. With the right approach, you can reinforce key concepts and sharpen problem-solving skills to perform at your best. This section will discuss how to use the available materials to help you prepare thoroughly for upcoming assessments.

One of the most efficient ways to prepare for tests is through consistent practice. By reviewing various problems, understanding the techniques for solving them, and applying those methods to new examples, you build confidence and readiness. Here’s how to make the most of the available study materials:

Focus on Key Topics

Before diving into practice exercises, take time to review the areas that are most likely to appear on the test. Understanding which topics are emphasized in your curriculum will allow you to focus your efforts on the most critical concepts. You can:

• Identify challenging areas: Review previous quizzes or practice tests to pinpoint areas where you struggled.
• Target weak spots: Focus more time on these areas to build a better understanding before the test.
• Use examples: Look at worked examples to understand the step-by-step process for solving problems in those topics.

Practice with Test-Like Problems

One of the most effective ways to prepare is to work through practice problems that resemble those you’ll encounter during the test. These can help familiarize you with the format and structure of questions. Practice exercises often highlight the types of questions most commonly asked and offer valuable insights into the time management needed for each task. To maximize your preparation:

• Complete practice worksheets: Use worksheets that simulate the actual test to build familiarity.
• Time yourself: Set a timer to replicate exam conditions, helping you become more efficient during the test.
• Review solutions: After completing exercises, carefully check your solutions to understand any mistakes and learn from them.

By using these strategies, you will be better prepared to face your test with confidence. Consistent practice and focused review are key to success. As you approach the exam day, remember that preparation is the best way to ensure you’re ready to tackle any challenge that comes your way.

Improving Problem-Solving Skills with Go Math

Mastering problem-solving requires a combination of critical thinking, practice, and strategy. By honing these skills, learners can approach challenges with more confidence and precision. This section will explore how using structured resources can help improve problem-solving abilities and develop a deeper understanding of various concepts.

One of the best ways to enhance problem-solving skills is through consistent practice and analysis. By regularly working through exercises, students can learn to break down complex problems into smaller, more manageable steps. The key is to approach each task methodically and use different strategies to find solutions. Below are some effective techniques to improve problem-solving capabilities:

Key Strategies for Effective Problem-Solving

To sharpen problem-solving abilities, it’s important to apply different techniques for various types of questions. Here’s a breakdown of some common strategies:

Strategy	Description
Understand the Problem	Carefully read and analyze the question to ensure you grasp the key information. Identify what is being asked and the data provided.
Break Down the Problem	Divide the problem into smaller, simpler parts to make it easier to solve. This will allow you to focus on one aspect at a time.
Visualize the Problem	Draw diagrams, charts, or tables to better understand the problem. Visual aids can often clarify the situation and make it easier to find a solution.
Check Your Work	Once you have found a solution, review your steps to ensure that everything adds up. This helps catch mistakes before finalizing the answer.

Practicing Problem-Solving with Examples

Applying these strategies to a variety of problems allows you to improve your problem-solving skills over time. Regularly practicing with examples that cover different topics will help you become more adaptable in solving diverse challenges. When you encounter difficulties, try breaking the problem into smaller parts and use different approaches to find the best solution.

By using structured practice materials, students can build the problem-solving techniques necessary for tackling complex questions. The more you practice and apply these strategies, the better equipped you’ll be to handle even the most challenging tasks with confidence.