
In this section, we explore the key concepts and techniques that will help students strengthen their problem-solving abilities. By focusing on core principles and offering detailed steps, this guide aims to simplify complex tasks and enhance understanding.
Through a structured approach, learners will discover how to break down challenges into manageable parts, making the process less intimidating. Clear explanations and practical examples support the development of skills that can be applied to a wide range of exercises.
Whether you’re reviewing prior knowledge or tackling new topics, this resource will ensure that students are well-equipped to tackle upcoming tasks with confidence. With each step clearly outlined, learners will be able to progress steadily and master essential skills for future success.
Go Math Grade 5 Lesson 1.8 Answers Overview
This section provides a comprehensive overview of the key solutions and techniques to tackle the exercises from the designated module. It offers a structured approach to understanding the core principles that are essential for mastering the material.
By breaking down each problem into clear, manageable steps, this guide helps students better grasp the concepts and gain confidence in applying their knowledge. Detailed explanations are designed to reinforce understanding and ensure that learners are able to approach similar tasks with ease.
Through careful analysis and practice, students can gain a deeper insight into the subject matter, improving both their problem-solving skills and their overall academic performance. The goal is to provide a clear roadmap to success, ensuring steady progress as students move forward in their learning journey.
Understanding Key Concepts in Lesson 1.8
In this section, we focus on the fundamental ideas that form the foundation of the exercises. Grasping these concepts is crucial for successfully solving problems and advancing to more complex topics. A clear understanding will allow learners to connect new knowledge with previous lessons, creating a strong base for continued growth.
The key principles explored in this section include strategies for breaking down tasks, recognizing patterns, and applying appropriate methods to find solutions. By reinforcing these ideas, students are better prepared to navigate through similar challenges with increased efficiency and confidence.
| Concept | Explanation |
|---|---|
| Breaking Down Problems | Dividing larger tasks into smaller, more manageable steps to simplify the process. |
| Recognizing Patterns | Identifying repetitive structures that help predict the next steps in problem-solving. |
| Applying Strategies | Using tried-and-tested methods to approach new challenges effectively. |
By focusing on these critical concepts, students will not only improve their problem-solving abilities but also build confidence in their skills, setting the stage for success in more advanced topics ahead.
Step-by-Step Solutions for Lesson 1.8
This section provides detailed instructions on how to approach each problem in a clear and methodical way. By breaking down the process into smaller, easy-to-understand steps, learners can follow a logical path to arrive at the correct solutions.
Each step is carefully explained to ensure that students understand the reasoning behind every action. This method not only aids in solving current problems but also helps build a solid foundation for tackling future challenges with similar structures.
The following examples illustrate how to apply the techniques step by step, making it easier to grasp complex concepts and strengthen problem-solving skills. By practicing these methods, students will gain confidence and proficiency in handling various types of tasks.
How to Tackle Lesson 1.8 Problems
Approaching challenges with a clear strategy is key to solving them effectively. The first step in any problem-solving process is understanding the requirements of the task. By breaking down each exercise into manageable components, students can focus on the most important aspects without feeling overwhelmed.
Identifying Key Information

Before diving into the calculations or steps, it’s essential to identify the key data provided in the problem. Look for numbers, terms, or relationships that will guide the approach. Highlighting or underlining important details ensures that nothing is overlooked.
Choosing the Right Approach

Once the essential information is gathered, choosing the best method for solving the problem becomes easier. Depending on the type of task, there are different strategies that can be applied, from simple operations to more complex reasoning.
| Step | Action |
|---|---|
| Step 1 | Identify key information and what is being asked. |
| Step 2 | Break down the problem into smaller, manageable parts. |
| Step 3 | Apply the appropriate method to solve each part. |
| Step 4 | Check the solution for accuracy and consistency. |
By following this approach, students can systematically work through any challenge, ensuring that each part of the process is addressed thoroughly and with confidence. Over time, this method will improve their problem-solving efficiency and understanding.
Important Tips for Success in Math
Achieving success in problem-solving requires more than just understanding the theory; it’s about developing the right habits and strategies. By implementing effective techniques, students can enhance their learning experience and tackle challenges with confidence.
Practice Regularly – Consistent practice is essential to mastering any skill. By engaging with different types of problems, students not only reinforce their understanding but also improve their ability to recognize patterns and apply appropriate solutions quickly.
Stay Organized – Keeping work neat and structured helps avoid mistakes and makes it easier to follow the logic behind each step. Using clear notation, labeling key parts of the problem, and breaking tasks into smaller sections will ensure clarity and reduce errors.
Ask Questions – Don’t hesitate to seek clarification when something is unclear. Whether through a teacher, peer, or online resource, getting help when needed will prevent confusion from building up and ensure that the concepts are well-understood.
Stay Patient and Positive – Patience is crucial, especially when faced with difficult tasks. Keep a positive mindset, and don’t get discouraged by challenges. Every problem solved, no matter how small, is progress and an opportunity for growth.
By adopting these strategies, students will be better equipped to face challenges and ultimately excel in their studies. Mastery comes with consistent effort, and the path to success is built one step at a time.
Common Mistakes to Avoid in Lesson 1.8
When working through exercises, it’s easy to overlook certain details that can lead to errors. By being aware of common mistakes, students can avoid unnecessary confusion and ensure a more accurate and efficient approach to solving problems.
Skipping Steps – One of the most frequent errors is rushing through a problem without following all the necessary steps. Skipping even a single part of the process can lead to incorrect solutions. It’s important to take the time to carefully follow each stage and check work as you go.
Misreading the Problem – Often, students get so focused on solving that they fail to fully understand the problem before starting. Take a moment to read the problem carefully and highlight or underline key information that will guide your approach. This small step can prevent costly mistakes later.
Incorrect Operations – Using the wrong operation for a particular task is a common mistake. For example, adding when subtraction is required or multiplying when division is needed can completely change the outcome. Always double-check which operation is appropriate for each part of the problem.
Not Reviewing Work – After completing a problem, many students forget to go back and review their work. This step is crucial for catching any errors that may have been made along the way. Taking a few extra minutes to verify each step can save time and improve accuracy.
Not Asking for Help – It’s easy to get stuck on a difficult problem, but failing to ask for assistance can lead to frustration and confusion. If something doesn’t make sense, don’t hesitate to seek help from a teacher, peer, or online resource. Getting clarification early on can prevent larger misunderstandings down the road.
By avoiding these common mistakes, students can improve their problem-solving skills and gain more confidence in their abilities. Staying focused and thoughtful throughout the process is key to success.
Practice Problems and Solutions for Mastery

To truly master any subject, consistent practice is essential. Engaging with a variety of problems allows learners to reinforce their understanding and apply concepts in different contexts. Below are several practice problems, along with step-by-step solutions, designed to strengthen key skills.
Problem Set 1: Basic Problem Solving
These problems focus on applying basic strategies and understanding fundamental concepts. Try to solve each one, following the steps outlined.
- Problem: A basket contains 12 apples. If each person takes 3 apples, how many people can share the apples?
- Problem: A piece of ribbon is 36 inches long. How many 6-inch pieces can be cut from it?
- Problem: A box contains 48 marbles. If you give 8 marbles to each friend, how many friends can receive marbles?
Solutions for Practice Set 1
- Solution for Problem 1: Divide 12 by 3 to find the number of people: 12 ÷ 3 = 4 people.
- Solution for Problem 2: Divide 36 by 6 to find how many pieces: 36 ÷ 6 = 6 pieces.
- Solution for Problem 3: Divide 48 by 8 to find how many friends can receive marbles: 48 ÷ 8 = 6 friends.
Problem Set 2: Applying Advanced Techniques
This set challenges learners to use more advanced problem-solving skills, requiring a deeper understanding of concepts.
- Problem: A train travels 60 miles per hour. How far will it travel in 3 hours?
- Problem: A rectangular garden is 15 feet long and 8 feet wide. What is the area of the garden?
- Problem: A book has 240 pages. If you read 15 pages per day, how many days will it take to finish the book?
Solutions for Practice Set 2
- Solution for Problem 1: Multiply speed by time: 60 × 3 = 180 miles.
- Solution for Problem 2: Multiply length by width to find area: 15 × 8 = 120 square feet.
- Solution for Problem 3: Divide total pages by pages per day: 240 ÷ 15 = 16 days.
By consistently practicing these problems and reviewing the solutions, students can build their confidence and enhance their ability to solve a variety of challenges. Each step is an opportunity for growth, bringing mastery closer with every attempt.
Mastering the Strategies in 1.8
To truly excel in problem-solving, it’s essential to master key strategies that simplify complex tasks. Understanding and applying effective techniques allow students to approach challenges with confidence and precision. By refining these methods, learners can tackle a wide range of problems with ease.
Breaking Down Complex Problems
One of the most important skills is the ability to break down complex problems into smaller, manageable parts. This approach not only makes the task less overwhelming but also helps identify the necessary steps to reach the correct solution. Chunking information into logical pieces is a powerful tool that can be applied to various problem types.
Using Logical Sequences for Accuracy
In addition to breaking problems into smaller steps, following a logical sequence ensures that each part of the problem is addressed properly. Systematic reasoning and following a clear order of operations reduce the chance of errors. Whether it’s performing calculations or identifying relationships, a step-by-step approach is key to getting the right answers.
By mastering these strategies, students will not only solve problems more efficiently but also build a deeper understanding of the underlying concepts. With practice, these methods become second nature, enabling learners to tackle even the most difficult problems with ease.
Why Lesson 1.8 Is Crucial for Understanding Math

Grasping the core concepts presented in this section is fundamental for building a solid foundation in problem-solving. The skills introduced here serve as the building blocks for more advanced topics, making it essential to fully understand the techniques before moving on to more complex ideas. Mastering these concepts ensures that students are equipped with the tools needed to tackle future challenges effectively.
Connecting Key Concepts
One of the key reasons this section is so vital is that it connects foundational ideas to real-world applications. By understanding the principles covered, learners are able to make meaningful connections between theory and practical use. This not only enhances retention but also helps to visualize how the skills can be applied in everyday situations.
Building Confidence for Future Learning
As students progress in their studies, they encounter increasingly difficult material. Having a firm grasp of these essential concepts allows them to approach new topics with confidence. Without this crucial understanding, students may struggle with more advanced material, making it harder to keep up. Strong comprehension at this stage provides a smoother path toward mastering more challenging problems later on.
In short, this section forms a critical part of a student’s learning journey, ensuring they have the necessary skills and confidence to succeed in future challenges. It prepares them for continued success and offers the tools to solve problems efficiently.
Breaking Down the Key Equations
Understanding the core equations is crucial for solving problems effectively. By breaking down each equation step by step, students can develop a deeper understanding of how different elements work together. This methodical approach helps to simplify complex problems and makes it easier to identify the necessary operations to reach a solution.
Step-by-Step Breakdown
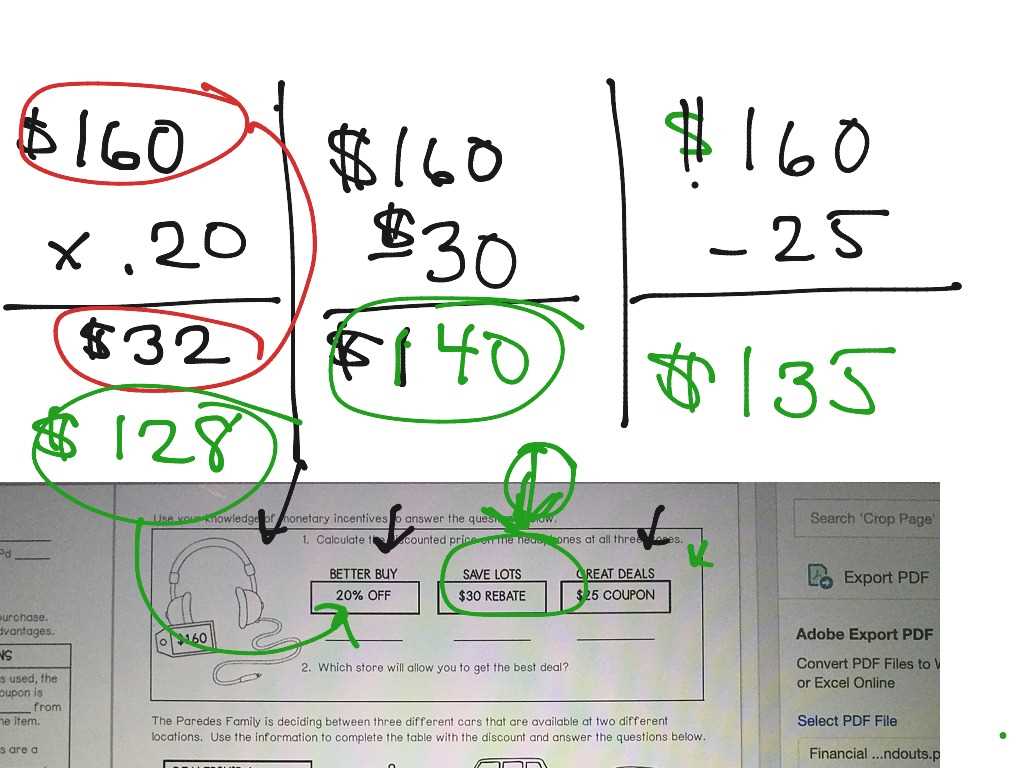
When tackling equations, it’s important to follow a structured approach. Start by identifying the components and operations involved, then apply them in the correct order. Below are the basic steps to follow when solving most equations:
- Identify the variables: Determine the unknowns that the equation is solving for.
- Understand the operations: Look at the addition, subtraction, multiplication, or division signs between the variables and constants.
- Perform operations: Carry out the operations step by step, always following the correct order (PEMDAS–parentheses, exponents, multiplication and division, addition and subtraction).
- Check the solution: After solving, review the equation to ensure the solution makes sense and satisfies the original equation.
Common Strategies for Simplification

There are several strategies to help simplify equations and make problem-solving more efficient:
- Combine like terms: Group terms that have the same variable to simplify the equation.
- Use inverse operations: Apply inverse operations (such as addition and subtraction) to isolate variables.
- Apply distributive property: Expand terms to simplify complex expressions.
By mastering these techniques and practicing regularly, students can confidently approach and solve equations with greater ease and accuracy. Understanding how to break down the steps in an equation ensures long-term success in solving more advanced problems.
How Lesson 1.8 Relates to Other Topics
The concepts introduced in this section play a significant role in understanding other areas of study. These principles build a solid foundation that supports future learning. By recognizing how the ideas connect to broader topics, students can appreciate the relevance and application of what they are learning. Understanding these relationships also strengthens their ability to apply skills in diverse problem-solving situations.
Connections to Future Concepts
The skills learned here are essential for grasping more complex ideas in subsequent lessons. The following topics are directly influenced by the foundational knowledge established in this section:
- Algebraic thinking: The principles learned here form the basis for solving algebraic expressions and equations in later topics.
- Data analysis: Understanding the relationships between numbers helps in interpreting data and calculating averages, percentages, and other measures in future studies.
- Geometry: The ability to break down complex problems and apply logical operations also supports geometry topics, such as calculating areas and volumes.
Real-World Applications
Beyond the classroom, the skills learned in this section are useful in various real-life situations. These concepts help in:
- Budgeting and financial planning: Basic operations and understanding relationships between numbers are crucial for managing finances.
- Problem-solving in daily life: Whether cooking, shopping, or planning a trip, these concepts help in making quick, accurate decisions.
- Engineering and technology: The ability to solve problems logically is a key skill in fields like engineering and computer science.
By understanding how the ideas in this section relate to other topics, students can see the broader picture and gain confidence in applying their knowledge to a variety of challenges.
How to Improve Your Math Skills

Improving your problem-solving abilities requires consistent practice and a deeper understanding of the underlying principles. By breaking down complex concepts and focusing on specific techniques, anyone can enhance their skills. It’s not just about memorizing formulas; it’s about developing the mindset to tackle new challenges with confidence and accuracy.
Effective Practice Techniques
One of the best ways to improve is through regular and focused practice. Consider the following strategies to boost your proficiency:
- Practice regularly: Consistency is key. Set aside time each day to work through problems and review concepts.
- Work on different types of problems: Challenge yourself with a variety of problems to strengthen different aspects of your skills.
- Review mistakes: Don’t shy away from errors. Understanding where you went wrong helps to prevent repeating the same mistakes.
Strengthening Conceptual Understanding
In addition to practicing problems, it’s important to focus on understanding the “why” behind each concept. This approach leads to long-term retention and the ability to apply knowledge in different contexts.
- Ask questions: If you’re unsure about a concept, ask questions. Clarifying doubts helps to solidify your understanding.
- Break down problems: Break problems into smaller, manageable steps to avoid feeling overwhelmed.
- Teach others: Teaching others is one of the most effective ways to reinforce your own understanding.
By incorporating these methods into your study routine, you’ll gradually see improvements in your ability to solve problems with ease and accuracy.
Understanding Word Problems in Lesson 1.8

Word problems are often seen as a challenge, but they are a great way to apply learned concepts to real-world situations. They require critical thinking and the ability to translate everyday scenarios into mathematical operations. By carefully reading and analyzing the problem, students can identify key information and determine the steps needed to find a solution.
The key to solving word problems is to break down the information step by step. Start by underlining or highlighting important numbers and terms in the problem. This helps you focus on what is being asked and what needs to be calculated. Once you identify these elements, you can begin to form an equation or set of instructions to arrive at the correct solution.
Another effective strategy is to visualize the problem. Drawing diagrams or making lists can help clarify complex situations and make it easier to solve. Once the solution is reached, it’s important to double-check the work to ensure that the answer makes sense in the context of the original question.
Efficient Study Tips for 5th Grade Math
Studying effectively for mathematical concepts involves more than just memorizing formulas or solutions; it’s about understanding the reasoning behind each concept. With the right strategies, you can master key ideas and build a strong foundation for future learning. Consistency, focus, and the right resources are essential for progress and success.
One of the best ways to retain and apply what you’ve learned is to break study sessions into manageable chunks. Rather than cramming all the material into one sitting, try reviewing a few concepts each day. This will help you stay focused and avoid feeling overwhelmed. Additionally, actively engaging with the material–through practice problems, discussions, or teaching others–will deepen your understanding and enhance retention.
Another effective technique is to use a variety of resources to reinforce your learning. Online tutorials, practice exercises, and interactive tools can offer new perspectives and reinforce what you’ve studied in class. Don’t hesitate to ask for help from teachers or peers when you’re stuck, as collaborative problem-solving often leads to deeper comprehension.
What to Expect from Go Math Series
The Go Math series is designed to provide a comprehensive approach to learning essential concepts and skills. It aims to build a deep understanding of key ideas through structured lessons and engaging exercises. Students can expect to encounter a wide variety of problems, ranging from simple tasks to more complex challenges that require critical thinking and problem-solving.
Each unit in the series progressively introduces new concepts, helping learners develop a strong foundation. The curriculum emphasizes conceptual understanding, allowing students to apply what they’ve learned in real-world situations. Along with lessons, the series includes practice exercises that reinforce learning and ensure mastery of the material.
What sets the Go Math series apart is its focus on interactive and visual learning. Students are encouraged to use visual aids, diagrams, and hands-on activities to help them grasp abstract concepts. This multi-faceted approach ensures that learners not only solve problems but also understand the underlying principles behind them, providing a well-rounded education.
How to Use the Answer Key Effectively

The answer key is a powerful tool that can help you identify areas where you need improvement and reinforce your understanding of key concepts. However, it is important to use it strategically to maximize its benefits. Rather than simply looking at the correct responses, consider using the key as a guide to analyze your thought process and pinpoint mistakes. This method will allow you to deepen your comprehension and ensure you’re not just memorizing solutions, but truly understanding the material.
Review Mistakes and Understand Solutions
When you make an error, don’t just look at the correct answer and move on. Instead, take time to carefully review each step in the provided solution. Try to understand why a certain approach works and how it aligns with the concepts you’ve been learning. By reflecting on your mistakes, you’ll strengthen your problem-solving skills and avoid repeating the same errors in the future.
Use the Key as a Learning Tool

Instead of waiting until you’ve completed all the problems, consider referencing the answer key during your study sessions if you’re unsure of a step or concept. This can prevent confusion and help you stay on track. However, it’s crucial not to rely on the key too heavily. Challenge yourself to work through problems independently before checking the solutions, as this will help reinforce your critical thinking skills and build confidence in your abilities.
Additional Resources for Go Math Students
For students seeking to enhance their learning experience, there are various supplementary materials available that can provide extra practice, in-depth explanations, and interactive exercises. These resources are designed to help reinforce concepts, clarify doubts, and offer more challenging problems for deeper understanding. Utilizing these tools can make a significant difference in mastering the topics and ensuring success in upcoming challenges.
Online Platforms and Tools
Many websites offer interactive exercises and detailed tutorials to further strengthen your skills. These platforms are designed to make learning engaging and more approachable. Some popular options include:
- Interactive Quizzes: Websites that provide timed quizzes help track progress and highlight areas of improvement.
- Video Tutorials: Watch step-by-step guides to understand how to solve complex problems effectively.
- Educational Games: Games that incorporate problem-solving tasks in a fun, challenging environment.
Supplementary Workbooks and Guides
If you prefer offline resources, there are numerous workbooks and reference guides that can help solidify the concepts learned. These often come with additional practice problems, solutions, and tips for better performance:
- Practice Workbooks: These contain exercises and examples similar to what you encounter in class, designed to reinforce key concepts.
- Answer Keys with Explanations: Some workbooks include answer explanations to help you understand the reasoning behind each solution.
- Study Guides: These guides break down the material into easy-to-understand summaries, making it easier to review before tests.
How Lesson 1.8 Prepares You for Future Lessons
This section lays the foundation for understanding advanced concepts that you will encounter in subsequent topics. By mastering the skills and strategies introduced here, students are better equipped to tackle more complex problems in future lessons. The key is in practicing these essential techniques, as they serve as building blocks for more challenging material later on. Through a structured approach, the concepts learned here are designed to enhance problem-solving abilities, logical thinking, and the overall ability to apply knowledge in various scenarios.
Building Strong Problem-Solving Skills
One of the primary benefits of this section is the development of strong problem-solving abilities. The techniques learned here are not only useful for the current material but also form the basis for more difficult exercises that involve:
- Identifying key information: Understanding how to pinpoint important details in complex problems.
- Applying strategies: Using learned methods to approach unfamiliar situations with confidence.
- Breaking down complex questions: Decomposing difficult problems into manageable parts to solve them step-by-step.
Enhancing Conceptual Understanding for Future Topics
Another critical aspect of this section is that it reinforces core concepts that will be essential for grasping more advanced topics. As you progress, the knowledge gained here will make it easier to:
- Master more intricate topics: Building on the concepts learned to understand more detailed and sophisticated material.
- Recognize patterns: Identifying recurring structures in different types of problems to streamline solving processes.
- Increase confidence: Strengthening the foundation will boost confidence when approaching new subjects and topics.