Go Math Grade 5 Textbook Answers and Solutions

Mastering the core concepts in mathematics requires understanding the fundamentals and tackling challenges with clarity. This section focuses on helping students build a strong foundation by offering detailed solutions and practical tips for various exercises. With the right guidance, complex problems become manageable, fostering both confidence and competence.

Each section is designed to break down key topics in a simple yet comprehensive manner, ensuring that students can grasp difficult ideas and apply them effectively. By practicing with step-by-step solutions, learners develop the necessary skills to solve problems independently.

Using these resources, students can refine their problem-solving techniques, gaining a deeper understanding of essential concepts such as fractions, decimals, and geometry. With a focus on clarity and precision, this guide provides the tools needed for academic success and long-term mathematical proficiency.

Go Math Grade 5 Textbook Answers Overview

In this section, we explore how to navigate the key sections of the fifth-grade curriculum, focusing on providing structured support for solving problems and understanding core concepts. The goal is to offer students a clear path to mastering each topic with practical exercises and detailed solutions that aid in their learning process.

By reviewing the provided solutions, students can develop a deeper understanding of the underlying principles and techniques needed to approach problems efficiently. This guide is designed to support the learning journey, helping learners reinforce their knowledge and enhance their skills in a systematic manner.

• Concept Breakdown: A comprehensive overview of the major topics covered in the curriculum.
• Problem-Solving Methods: Step-by-step approaches for tackling typical challenges encountered in exercises.
• Clarifying Key Principles: Simplifying complex ideas to make them more accessible and easier to apply.
• Practical Exercises: Providing practice problems that reinforce newly learned skills and techniques.
• Visual Aids: Utilizing diagrams and illustrations to better explain abstract concepts and improve comprehension.

This approach ensures that learners not only solve problems but also understand the “why” behind each solution, giving them the tools to succeed in future lessons. By using these resources, students are better equipped to handle both simple and complex questions, developing confidence as they progress through the curriculum.

Understanding Key Concepts in Go Math

Grasping the foundational principles in elementary-level subjects is essential for building a solid academic base. This section focuses on breaking down the core topics and helping students understand the basic concepts that form the foundation of more advanced material. By mastering these key ideas, students can tackle progressively complex problems with confidence.

Core Ideas in Numerical Operations

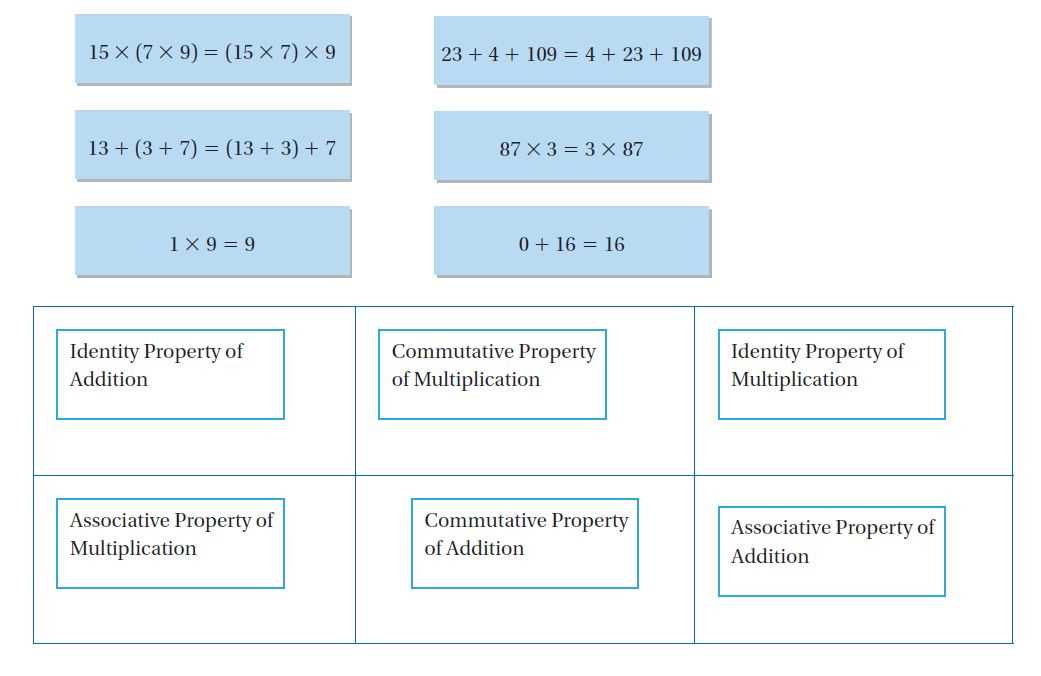
The ability to perform operations with numbers is a fundamental skill. Understanding how to work with whole numbers, fractions, and decimals provides the necessary foundation for tackling a wide range of problems. Mastery of addition, subtraction, multiplication, and division is crucial for advancing to higher-level calculations and problem-solving.

Exploring Shapes and Measurements

Understanding geometric shapes, their properties, and how to measure them is another vital concept. From identifying basic shapes to calculating areas and volumes, a firm grasp of these topics prepares students for future studies in geometry. Accurate measurement skills are also essential for applying mathematical principles to real-world scenarios.

Step-by-Step Solutions for Grade 5

Breaking down problems into manageable steps is an essential approach for mastering any subject. This section offers a detailed, step-by-step method for solving typical problems found in fifth-level exercises. By following these clear instructions, students can easily track their progress and build their problem-solving skills incrementally.

Each solution is carefully outlined to guide learners through every phase of the problem. The breakdown emphasizes key strategies and explains why each step is important, allowing students to understand not only how to arrive at the correct answer, but also the reasoning behind it. This method helps to reinforce understanding and encourages independent thought.

With consistent practice, students can apply these techniques to new challenges, improving both their speed and accuracy in solving various types of problems. By learning to approach exercises with confidence and structure, students gain the skills necessary to succeed in more advanced topics.

Common Challenges in Go Math 5

Many students face obstacles when learning new concepts, especially when those concepts become more complex. In this section, we address the most common difficulties encountered by learners at this stage. Understanding these challenges is crucial, as it helps students and educators identify areas that require additional focus and practice.

One of the most frequent difficulties is mastering fractions. While the basic idea of fractions may seem straightforward, applying them in different contexts–such as addition, subtraction, and multiplication–can cause confusion. Many students struggle with visualizing fractions, especially when they involve mixed numbers or denominators that are not the same.

Another challenge often arises with word problems. These problems require students to extract relevant information from a narrative and translate it into mathematical operations. This process of interpretation and decision-making can be tricky, as students need to identify the correct method to solve the problem, which may not always be immediately apparent.

Additionally, understanding geometric concepts like area, volume, and spatial relationships can pose problems for some students. The abstract nature of shapes and their properties requires a strong foundation in visualization and measurement, which may take time for some learners to fully grasp.

By recognizing and addressing these common hurdles, students can focus on developing the necessary skills to overcome them, paving the way for greater academic success.

How to Approach Word Problems

Word problems can often seem intimidating, but breaking them down into manageable steps makes them much easier to solve. The key is to understand the scenario, identify the relevant information, and figure out which operations are required. Here is a structured approach to successfully tackle these types of challenges.

1. Read the problem carefully: Ensure that you fully understand the story or situation being described. Sometimes, re-reading the problem helps to clarify the main idea and prevent misunderstandings.
2. Highlight key information: Identify important numbers, keywords, and any given conditions. These clues will guide you toward the solution.
3. Determine what is being asked: Clearly identify what the problem is asking for. Are you looking for a total, a difference, a comparison, or something else? This will tell you which operation to apply.
4. Choose the right strategy: Based on the information, decide what mathematical operations are needed. Whether it’s addition, subtraction, multiplication, or division, knowing the appropriate operation is critical.
5. Set up the equation: Translate the words into numbers and symbols. This step involves writing down the math statement that corresponds to the word problem.
6. Solve and check your work: After performing the necessary calculations, double-check your solution to make sure it makes sense in the context of the problem.

By following these steps, students can build a methodical approach to word problems, making them less overwhelming and easier to solve. Practice and patience will lead to improved skills and confidence in handling complex scenarios.

Mastering Fractions with Go Math

Understanding fractions is a critical skill that forms the foundation for more advanced topics. To master this concept, students must first grasp the basic principles before moving on to more complex operations. This section focuses on building a solid understanding of fractions, helping students become more confident in working with them across various situations.

Key Concepts in Fraction Mastery

Before diving into operations like addition and subtraction, it’s important to understand the building blocks of fractions:

• Numerators and Denominators: The top number represents the number of parts being considered, while the bottom number indicates the total number of equal parts.
• Equivalent Fractions: Different fractions that represent the same value, such as 1/2 and 2/4.
• Simplifying Fractions: Reducing fractions to their simplest form by dividing both the numerator and denominator by their greatest common factor.
• Comparing Fractions: Determining which of two fractions is larger or smaller by finding a common denominator or using other comparison methods.

Steps to Master Fractions

Once the basic concepts are understood, it’s time to apply them through practical exercises. Here are key steps to mastering fractions:

1. Practice with Simple Fractions: Start with fractions that have small, easy-to-understand numbers to build familiarity.
2. Use Visual Aids: Diagrams and models are effective tools for visualizing fractions, helping students see how they relate to whole numbers and each other.
3. Perform Operations with Fractions: Practice adding, subtracting, multiplying, and dividing fractions step-by-step to gain fluency in their manipulation.
4. Apply Fractions to Real-Life Scenarios: Using fractions in everyday situations, such as cooking or measuring, reinforces their practical value and deepens understanding.

With consistent practice and a clear understanding of these fundamental principles, students can confidently master fractions and apply them effectively in both academic and real-world contexts.

Decimals and Their Applications Explained

Decimals are an essential part of everyday calculations, especially when precision is required. They provide a way to represent values between whole numbers, making it easier to express measurements, currency, and many other real-world quantities. Understanding decimals and how to work with them is crucial for solving many types of problems accurately.

Decimals are based on powers of ten and are used to express parts of a whole in a way that is easier to understand and work with than fractions. By learning how to add, subtract, multiply, and divide decimal numbers, students can apply these skills in various practical scenarios, from shopping to cooking and beyond.

In real-life applications, decimals are widely used in areas such as:

• Money and Currency: Decimals are often used to represent cents in dollars, or fractions of other currencies, making them essential for everyday transactions.
• Measurement: Many measurements, like weight, length, or temperature, are often recorded using decimal values to ensure accuracy.
• Time: Time calculations, especially in hours, minutes, and seconds, often involve decimal fractions.
• Data and Statistics: Decimals are used to represent averages, percentages, and other statistical values, offering a clear way to interpret data.

By practicing decimal operations and recognizing their importance in practical situations, students can enhance their numerical fluency and apply their knowledge in a wide range of contexts. Understanding how to handle decimals effectively opens the door to solving more complex problems in various fields.

Effective Problem-Solving Strategies

Problem-solving is a vital skill that extends beyond academics, helping individuals navigate challenges in everyday life. Developing strong problem-solving abilities involves breaking down complex situations into simpler, manageable steps. This section focuses on strategies that can help students tackle problems with confidence and accuracy.

The key to successful problem-solving lies in understanding the problem fully before jumping to a solution. This process involves carefully reading the problem, identifying the necessary information, and choosing the most appropriate approach. By developing a systematic method, students can avoid common mistakes and reach the correct solution more efficiently.

Some effective strategies include:

• Visualization: Drawing diagrams, charts, or models can make abstract concepts clearer and easier to manipulate.
• Working Backwards: When a problem seems too complicated, starting from the desired outcome and working backwards can help identify the steps needed to reach the solution.
• Breaking Down the Problem: Dividing a larger problem into smaller, simpler tasks makes it less overwhelming and more manageable.
• Checking Work: Once a solution is reached, reviewing the steps and the final answer ensures the solution is correct and aligns with the problem’s conditions.
• Trial and Error: For some problems, testing different approaches can lead to finding the correct solution by process of elimination.

By applying these strategies consistently, students can improve their ability to approach and solve problems in a structured and efficient way. These techniques not only lead to better academic outcomes but also develop critical thinking skills that are valuable in all areas of life.

Understanding Geometry in Grade 5

Geometry is a branch of mathematics that deals with shapes, sizes, and the properties of space. In the fifth level of learning, students begin to explore more advanced concepts related to geometric figures, their attributes, and their relationships to one another. Mastering these concepts is crucial, as they form the foundation for more complex geometric principles encountered in later education.

At this stage, students start by recognizing different types of shapes, learning their properties, and understanding how to measure and compare them. The ability to visualize and classify various figures helps to strengthen spatial awareness, which is vital in many real-world scenarios like architecture, design, and engineering.

Key concepts covered in fifth-level geometry include:

• Two-Dimensional Shapes: Identifying and classifying common shapes such as squares, rectangles, triangles, and circles based on their properties like sides, angles, and symmetry.
• Angles: Understanding different types of angles, including acute, obtuse, and right angles, and how to measure them using a protractor.
• Perimeter and Area: Calculating the perimeter and area of various shapes, which are essential skills for understanding how much space a shape covers or how far its boundary extends.
• Symmetry: Recognizing symmetrical shapes and learning how to fold or reflect them to identify symmetrical halves.
• Volume of Solids: Introducing three-dimensional shapes and learning how to calculate their volume using appropriate formulas.

By understanding these basic principles, students gain a deeper insight into the world around them and develop critical thinking skills that are useful in everyday life, from measuring objects to understanding architectural designs and more. These early geometric concepts lay the groundwork for more advanced studies in later years.

Tips for Improving Accuracy in Problem Solving

Achieving precision in solving problems requires a combination of focus, practice, and systematic approaches. Small mistakes can lead to incorrect results, which is why it’s essential to develop strategies that ensure accuracy at each step. This section highlights practical tips that can help students avoid common errors and improve their problem-solving skills.

Developing Good Habits

The foundation of accuracy lies in establishing effective habits that guide the entire problem-solving process. These habits ensure that each step is thoroughly checked and that no important detail is overlooked.

• Read Carefully: Always read the problem in its entirety before beginning to solve it. Pay close attention to every detail, as even small changes in wording can alter the approach needed.
• Double-Check Work: After solving the problem, go back and check each step to ensure no errors were made, especially in calculations or logic.
• Show Work: Writing down each step, no matter how simple, helps to avoid missing important information and makes it easier to track any mistakes.

Practicing with Purpose

Frequent practice with a focus on technique and accuracy is essential for improving problem-solving skills. The more familiar students are with the processes involved, the more naturally they can approach new problems.

• Work on Simpler Problems First: Start with basic problems to build confidence and improve speed, gradually progressing to more complex ones as your understanding deepens.
• Use Tools Wisely: Leverage resources such as calculators, protractors, or charts to help reduce calculation errors, but ensure that the underlying concepts are fully understood.
• Take Breaks: Avoid rushing through problems by taking short breaks to refresh the mind. A clear mind leads to more accurate results.

By implementing these strategies, students can develop a disciplined approach to solving problems, reducing mistakes and improving their ability to tackle even the most challenging tasks with confidence.

Building Confidence with Problem Solving

Developing confidence in solving problems is an essential part of the learning process. When students feel assured in their ability to tackle challenges, they are more likely to approach each task with determination and clarity. Confidence doesn’t just come from getting the right answers but from understanding the process, learning from mistakes, and gradually mastering new concepts.

Fostering a Growth Mindset

Encouraging a growth mindset is key to building confidence in any subject. When students believe that their abilities can improve with practice, they are more likely to take on challenging problems without fear of failure. Instead of focusing solely on results, it’s important to highlight the progress made through effort and perseverance.

• Embrace Mistakes: Mistakes are an opportunity to learn. Emphasizing that errors are a natural part of learning helps reduce the fear of failure and encourages risk-taking in problem solving.
• Celebrate Small Wins: Recognizing even small achievements boosts morale and motivates students to keep progressing. Acknowledging improvements helps build their self-esteem.
• Focus on Understanding: Students should focus on mastering concepts rather than memorizing answers. A deep understanding of the material leads to greater confidence in applying knowledge in various situations.

Consistency and Practice

Consistent practice is a proven way to boost confidence. The more often students work through problems, the more familiar they become with different problem-solving methods. Over time, this repetition helps reinforce skills and reduces anxiety when approaching new tasks.

• Start Simple: Begin with easier problems to build a solid foundation. As confidence grows, gradually introduce more complex challenges.
• Practice Regularly: A consistent schedule of practice helps solidify learning and increase familiarity with different problem types.
• Reflect on Progress: Periodically reviewing past work allows students to see how much they have improved and reinforces their belief in their ability to succeed.

By creating an environment that values persistence, understanding, and regular practice, students will gradually gain the confidence to tackle any problem, knowing that they have the skills to find the right solutions.

How to Use Textbook Solutions Effectively

Understanding how to leverage solution guides can significantly enhance a student’s problem-solving skills. While these resources offer the final answers, they are most useful when used as a tool for learning rather than simply providing a shortcut. To maximize their effectiveness, it’s important to approach them thoughtfully and strategically.

Focus on the Process, Not Just the Answer

Rather than jumping straight to the final solution, take the time to carefully study the steps leading to the result. This allows students to see the reasoning behind each step, helping them grasp the concepts more thoroughly. The solution process should be viewed as a guide to understanding the logic behind solving similar problems in the future.

• Step-by-Step Breakdown: Focus on understanding each step in the process. Identify why each action was taken and how it leads to the next step.
• Identify Key Concepts: As you work through the solution, highlight important principles and techniques that can be applied to other problems.
• Take Notes: Jot down any strategies or tips that can be helpful for similar problems in the future.

Use Solutions to Check Your Work

Solution guides can serve as an essential tool for verifying your own work. After attempting a problem, comparing your approach with the provided solution can help identify any mistakes and clarify areas where your understanding may need improvement.

• Compare Your Steps: Review each step in the solution and compare it with your own work. Are there any differences in the method or reasoning?
• Learn from Mistakes: If your answer differs, try to understand why. Are there any steps you missed or misunderstood? Use the guide to help address these gaps.
• Reattempt Challenging Problems: After reviewing the solution, attempt the same or similar problems again. This reinforces the correct approach and builds confidence in problem-solving.

When used correctly, solution guides become a powerful tool for learning, not just a way to get quick answers. By focusing on understanding the process and using them for self-checking, students can deepen their knowledge and improve their skills.

Interactive Learning with Go Tools

Interactive learning tools offer students a dynamic and engaging way to explore new concepts and reinforce their skills. By providing a hands-on approach to learning, these resources make complex ideas more accessible and fun. When integrated into the learning process, interactive tools encourage active participation and foster a deeper understanding of the material.

These tools can range from digital platforms and apps to in-class activities that offer instant feedback. Using them effectively can help students retain information better and develop a more intuitive grasp of problem-solving techniques.

Engaging Digital Platforms

Digital platforms play a crucial role in interactive learning by providing instant access to practice problems, tutorials, and explanations. Many of these platforms allow students to work at their own pace, offering personalized learning experiences.

• Instant Feedback: Digital platforms can provide immediate feedback on student responses, helping them quickly identify areas for improvement.
• Interactive Exercises: These platforms offer engaging exercises that make learning feel more like a game, helping to motivate students to continue practicing.
• Progress Tracking: Many tools include progress tracking, allowing students and teachers to monitor improvement over time and target specific areas of difficulty.

Hands-On Classroom Activities

Interactive classroom activities also play a significant role in making learning more enjoyable. By incorporating group discussions, collaborative problem-solving, and physical manipulatives, students can develop a deeper understanding of abstract concepts through practical application.

• Group Collaboration: Working together on problems helps students learn from each other and develop teamwork skills.
• Visual Learning Tools: Manipulatives like blocks, charts, and diagrams provide a visual representation of concepts, making them easier to understand.
• Real-Life Applications: Connecting lessons to real-life situations through interactive scenarios makes the material more relevant and easier to grasp.

By incorporating a mix of digital tools and hands-on activities, students can enjoy a well-rounded and interactive learning experience that enhances their understanding and retention of key concepts.

Reviewing Key Operations in Grade 5

Mastering fundamental operations is essential for students to succeed in solving complex problems and building a strong foundation for future learning. At this stage, students refine their skills in various techniques, focusing on ensuring accuracy and efficiency. Each operation forms a critical component of their problem-solving toolkit, and revisiting these core principles helps reinforce their understanding.

By consistently reviewing and practicing these essential skills, students improve their ability to handle more advanced concepts with confidence. Understanding how to apply these operations in different contexts is key to becoming proficient in tackling real-world challenges.

Addition and Subtraction Mastery

At this level, students focus on refining their addition and subtraction skills, which are the building blocks for more complex operations. These basic calculations are used in a variety of scenarios, such as solving word problems and working with larger numbers. It’s essential to build speed and accuracy when performing these operations.

• Multi-digit Addition and Subtraction: Understanding how to handle multi-digit numbers effectively is essential for solving both simple and complex problems.
• Regrouping (Carrying and Borrowing): Mastery of regrouping is a crucial skill that ensures students can handle larger numbers accurately.
• Application in Real-World Problems: Students are encouraged to apply these operations in practical contexts, such as budgeting or measuring distances.

Multiplication and Division Concepts

Multiplication and division are fundamental operations that require a deep understanding of patterns and relationships. These concepts are essential for solving a wide variety of problems, from simple calculations to more complex mathematical tasks.

• Multiplication of Larger Numbers: Developing fluency in multiplying larger numbers allows students to tackle problems that involve multi-step calculations.
• Understanding Division as Repeated Subtraction: Understanding division not just as a process but as repeated subtraction aids in grasping more abstract concepts like fractions.
• Fact Families and Patterns: Recognizing the relationship between multiplication and division fact families helps students build mental math skills.

By continuously practicing these key operations, students not only solidify their foundational knowledge but also increase their confidence in applying these skills across different problem types.

Helping Students with Homework

Supporting students with their assignments is crucial for reinforcing concepts and ensuring a thorough understanding of key topics. Homework often provides the opportunity to practice and apply learned material, but it can also be challenging without the right guidance. Helping students navigate these tasks effectively allows them to build confidence and develop independent problem-solving skills.

When assisting with assignments, it’s important to focus on guiding students through the thought process rather than simply providing solutions. This approach encourages critical thinking and helps students gain a deeper understanding of the material. Below are some strategies to help students succeed with their assignments.

Breaking Down Problems

Students often struggle with complex problems because they may feel overwhelmed by the number of steps involved. One effective method is to break down problems into smaller, more manageable parts. This allows students to focus on one aspect at a time, making the task feel less daunting.

• Step-by-Step Approach: Teach students to identify each part of the problem and tackle it sequentially.
• Understanding Key Information: Help students highlight important details in the problem to understand what is being asked.
• Revisiting Previous Steps: Encourage students to check their work after each step to ensure accuracy before proceeding.

Using Visual Aids and Resources

Visual aids and tools can help students grasp complex concepts more effectively. Diagrams, charts, and online resources provide an alternative way of explaining abstract ideas, making them more tangible.

Resource	Benefit	How to Use
Diagrams and Drawings	Helps visualize relationships and solve problems with spatial reasoning.	Encourage students to sketch out problems to better understand the solution process.
Online Tools and Games	Provides interactive practice and reinforces concepts through repetition.	Guide students to reliable online resources to practice similar problems.
Reference Materials	Helps clarify concepts and provides examples of similar problems.	Encourage students to refer to textbooks or notes for additional explanations.

By providing the right support and encouraging independence, students can not only complete their homework successfully but also develop a stronger grasp of the concepts being taught.

Understanding Go Math’s Learning Approach

The learning approach used in Go Math is designed to provide students with a structured and engaging way to grasp complex concepts. It emphasizes a gradual progression from basic skills to more advanced topics, allowing learners to build a solid foundation. This method fosters both conceptual understanding and practical problem-solving abilities, making learning more intuitive and effective.

At the heart of this approach is the idea of mastery learning. Instead of rushing through topics, students are encouraged to fully understand each concept before moving on to the next. This ensures that they are well-prepared for more challenging material and helps boost their confidence along the way.

Key Features of the Learning Approach

The program incorporates various strategies to keep students engaged while promoting deep understanding. Here are some key aspects of Go Math’s learning approach:

• Visual Learning Tools: The curriculum integrates diagrams, models, and visual representations to make abstract concepts more accessible.
• Interactive Practice: Students can engage with problems in a hands-on manner, using digital tools and exercises to reinforce their learning.
• Conceptual Understanding: The focus is not just on memorizing formulas but also on understanding the reasoning behind each concept.

Building Confidence Through Structured Practice

One of the primary goals of this approach is to help students build confidence in their abilities. By providing a step-by-step guide through various types of problems, students can practice each skill at their own pace. This structured practice ensures that learners are never overwhelmed and that they can see their progress over time.

• Frequent Review: Periodic review sessions help students retain what they’ve learned and identify areas where they may need further assistance.
• Clear Explanations: Each topic is broken down into manageable segments with clear, concise explanations that students can easily follow.

By combining these strategies, Go Math aims to create an environment where students not only succeed academically but also enjoy the learning process, laying the groundwork for continued success in the future.

Using Additional Resources for Extra Practice

Supplementing standard materials with additional resources is a key strategy for reinforcing skills and enhancing understanding. These tools offer students the opportunity to practice concepts beyond what’s covered in regular lessons, helping to solidify their knowledge and improve performance. When students use extra practice materials, they can approach challenging topics from different angles, leading to a deeper grasp of the material.

Additional resources provide a range of exercises and explanations that allow learners to practice at their own pace. These resources come in various formats, from interactive online platforms to printable worksheets, making it easier for students to find the method that works best for them.

Types of Resources to Enhance Learning

To ensure comprehensive practice and understanding, students can turn to several types of supplementary tools:

• Online Platforms: Websites and apps offering interactive exercises provide immediate feedback, helping students to identify mistakes and learn from them.
• Printable Worksheets: Physical worksheets allow students to practice problems away from screens, offering a more traditional method of reinforcement.
• Study Guides: Comprehensive study guides break down topics step-by-step, providing extra explanations and examples for students to work through.
• Video Tutorials: Video lessons offer visual demonstrations and additional insights into complex topics, aiding in concept retention.

How to Effectively Use Extra Practice Materials

For maximum benefit, it’s important to use these resources in a structured way. Here’s how students can make the most out of their extra practice sessions:

Step	Action	Purpose
1	Review the lesson or concept	Ensure understanding before moving on to practice
2	Complete practice exercises	Reinforce skills through hands-on practice
3	Check answers and review mistakes	Identify areas of weakness and correct errors
4	Revisit difficult concepts	Strengthen understanding by reworking challenging problems

By integrating extra practice into their study routines, students can enhance their understanding, boost confidence, and prepare themselves for more advanced topics. Consistent use of these resources leads to improved mastery and greater academic success.