Integrated Math 1 Final Exam Answers and Solutions

Success in mathematics requires a deep understanding of various fundamental principles. Whether you’re preparing for a comprehensive assessment or simply looking to refine your skills, grasping the core concepts is crucial. This section is designed to help you tackle the most important topics and challenges that you may encounter in your course.

Comprehension of algebra, geometry, and basic functions plays a significant role in problem-solving. By focusing on critical areas like equations, graphs, and statistical methods, you’ll be equipped to approach even the most complex problems with confidence. This guide offers detailed solutions and strategies to help you achieve your best performance.

As you move forward, keep in mind that practice and consistency are key to success. With the right tools and techniques, mastering these subjects will become not only achievable but also rewarding. Prepare effectively and approach every question with clarity and confidence.

Integrated Math 1 Final Exam Answers

This section provides a comprehensive guide to solving various types of problems encountered during your assessment. Mastery of key concepts is essential for achieving success, and understanding the process behind each solution can significantly improve your performance. By focusing on the most common question types and offering step-by-step solutions, you’ll be able to approach each challenge with confidence.

Common Problem Types and How to Approach Them

Throughout your studies, you will encounter several problem types that require different techniques for solving. Below are some of the most common areas that often appear on assessments:

• Linear Equations: Learn to solve for unknowns in various scenarios, from simple equations to more complex systems.
• Graphing Functions: Understand the relationship between equations and their graphical representations.
• Polynomials: Master the art of factoring and simplifying polynomial expressions.
• Statistics: Work with data sets, mean, median, mode, and probability calculations.
• Geometry Problems: Apply geometric formulas to solve for area, perimeter, volume, and angles in various shapes.

Step-by-Step Problem Solving Strategy

To efficiently solve problems, consider the following steps:

1. Understand the Problem: Read through the question carefully to identify key information.
2. Identify Relevant Formulas: Recognize which formulas or principles apply to the given problem.
3. Apply Logical Steps: Break down the problem into smaller, manageable parts and solve step-by-step.
4. Check Your Work: After arriving at an answer, review each step to ensure accuracy and consistency.

By practicing these techniques and familiarizing yourself with common question structures, you’ll be better prepared to approach and solve problems efficiently during your assessment.

Overview of Integrated Math 1

This section offers a broad understanding of the foundational concepts that are crucial for solving a variety of mathematical problems. The course focuses on building essential skills such as algebraic manipulation, working with geometric figures, and interpreting data through statistical methods. A solid grasp of these topics is necessary for success in both academic and real-life applications.

Core Topics Covered

The primary areas of focus in this course include:

• Algebra: Understanding variables, equations, and expressions to solve problems efficiently.
• Geometry: Exploring shapes, angles, and geometric principles to analyze spatial relationships.
• Statistics and Probability: Interpreting and analyzing data, calculating averages, and assessing likelihoods.
• Functions and Graphs: Visualizing relationships between variables and interpreting mathematical models.

Importance of These Topics

By mastering these areas, students not only gain the necessary skills for higher-level courses but also improve their problem-solving abilities in daily life. These concepts form the foundation for more advanced studies in various branches of mathematics, and understanding them deeply ensures success in future learning endeavors.

Key Concepts for the Final Exam

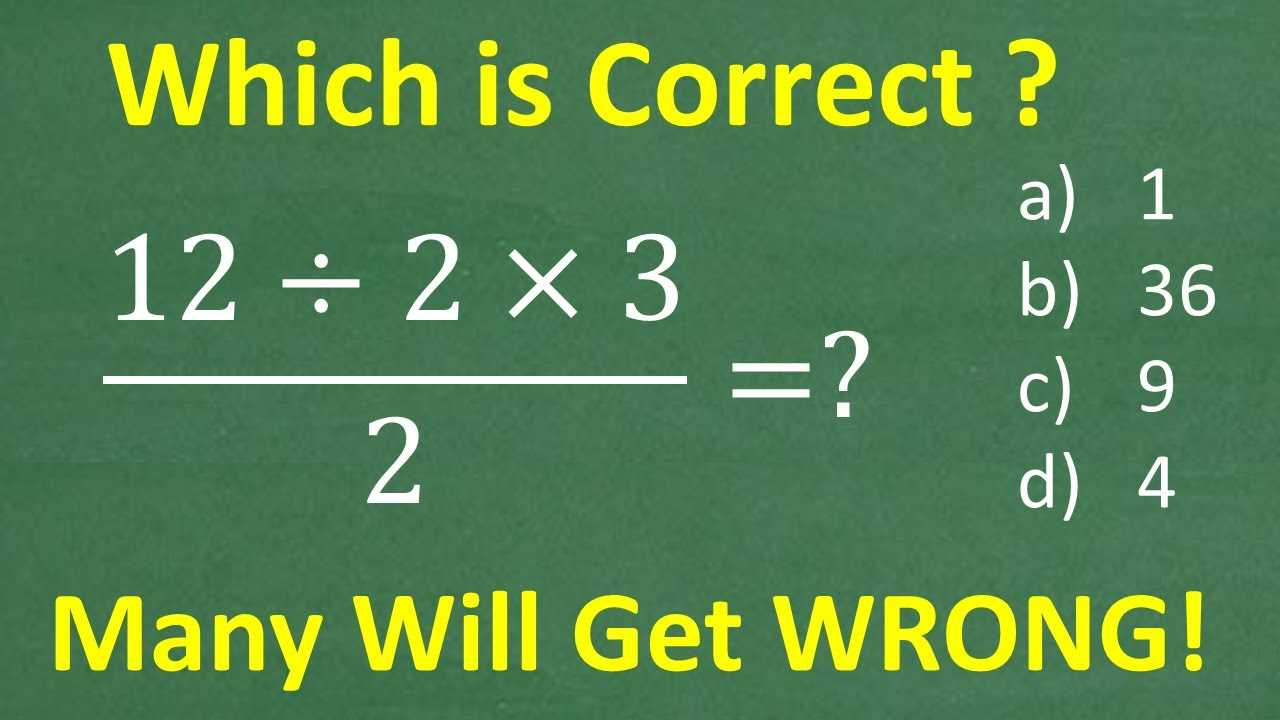
To succeed in any comprehensive assessment, it is essential to understand the core principles and techniques that are most likely to appear. These concepts are fundamental to solving problems accurately and efficiently, as they provide the tools needed to tackle a variety of question types. Familiarizing yourself with these key ideas will help you approach each problem with confidence and clarity.

Focus on mastering the following core areas:

• Solving Equations: Understand how to isolate variables and solve for unknowns in linear and quadratic equations.
• Graphing Relationships: Be comfortable plotting functions and interpreting the behavior of graphs.
• Geometric Principles: Apply formulas for area, perimeter, and volume, as well as solving for unknown angles in geometric shapes.
• Working with Polynomials: Practice factoring, simplifying expressions, and solving polynomial equations.
• Statistics and Data Analysis: Gain proficiency in calculating measures of central tendency, interpreting data, and understanding probability.

Mastering these concepts will not only prepare you for the challenges ahead but also enhance your problem-solving skills, enabling you to tackle even the most complex tasks with ease.

Common Topics Covered in the Exam

Understanding the key areas that are typically covered in assessments can help you focus your study efforts and approach the test with confidence. These topics form the foundation for solving a wide variety of problems, and being familiar with them will increase your chances of success. Below are the common subjects that are often emphasized in such evaluations.

Essential Areas of Focus

During your preparation, pay close attention to the following topics:

• Linear and Quadratic Equations: Master solving equations involving variables and constants, including both simple and more complex forms.
• Geometry Basics: Learn about shapes, area, perimeter, volume, and how to calculate missing angles in different geometric figures.
• Functions and Graphing: Become proficient in plotting graphs and interpreting the relationship between variables in various functions.
• Data Analysis and Statistics: Understand how to calculate measures like mean, median, mode, and how to analyze data sets for patterns.
• Polynomials and Factoring: Practice factoring polynomials and simplifying algebraic expressions to solve problems efficiently.

Problem-Solving Techniques

Familiarity with these topics will help you approach a wide range of questions. Practice solving problems from each area to strengthen your problem-solving skills and boost your confidence during the assessment.

How to Prepare for the Final

Effective preparation is key to performing well in any comprehensive assessment. By focusing on the most important concepts and using efficient study strategies, you can ensure that you are ready to tackle the challenges ahead. The process involves reviewing essential topics, practicing problem-solving techniques, and managing your time wisely.

1. Review Core Concepts: Start by revisiting the main areas covered throughout your course. These include algebra, geometry, data analysis, and basic functions. Make sure you understand the fundamental principles behind each topic, as these are often the building blocks for more complex problems.

2. Practice with Sample Problems: Working through practice questions is one of the most effective ways to prepare. Focus on problems that challenge your understanding and help reinforce your skills. This will also help you become familiar with the types of questions you may encounter during the assessment.

3. Time Management: Set aside dedicated time each day for review and practice. Create a study schedule that allows you to cover all necessary topics without feeling overwhelmed. Be sure to balance your time between learning new concepts and reinforcing what you already know.

4. Review Mistakes: After solving practice problems, take time to review any errors. Understanding why you made a mistake is critical to avoiding it in the future. This will also help you identify areas that may need more attention before the assessment.

5. Stay Positive and Confident: Confidence plays a crucial role in doing well. Approach the preparation process with a positive attitude, and remember that consistent practice and review will lead to improvement.

Solving Algebraic Equations Step by Step

Solving equations is a fundamental skill that forms the basis of many mathematical problems. To solve an equation successfully, it’s important to follow a structured process that allows you to isolate the variable and find its value. In this section, we will break down the steps to approach and solve various types of equations, from simple to more complex forms.

Step-by-Step Process

Here is a general method you can follow to solve most equations:

• Step 1: Simplify both sides of the equation: Eliminate parentheses and combine like terms to make the equation as simple as possible.
• Step 2: Move terms involving the variable to one side: Use addition or subtraction to get all variable terms on one side of the equation and constants on the other.
• Step 3: Isolate the variable: Use multiplication or division to isolate the variable and solve for its value.
• Step 4: Check your solution: Substitute the value of the variable back into the original equation to ensure both sides are equal.

Example: Solving a Linear Equation

Consider the equation:

3x + 5 = 11

• Step 1: Subtract 5 from both sides: 3x = 6
• Step 2: Divide both sides by 3: x = 2
• Step 3: Check the solution: Substitute x = 2 back into the original equation: 3(2) + 5 = 11, which simplifies to 6 + 5 = 11, confirming the solution is correct.

By following these steps, you can solve any linear equation systematically and accurately.

Understanding Geometry on the Exam

Geometry is a significant part of many assessments, and understanding its key concepts is essential for success. The ability to recognize different shapes, understand spatial relationships, and apply geometric principles is vital. In this section, we will explore the main geometry concepts you need to be familiar with and offer tips for solving geometric problems efficiently.

Key Concepts in Geometry

In any assessment involving geometry, you will encounter several fundamental topics. These include understanding various shapes, calculating areas and volumes, and working with angles. Below is a table summarizing some of the most common geometric elements that may appear in questions:

Shape	Formula for Area	Formula for Perimeter	Additional Information
Rectangle	Length × Width	2 × (Length + Width)	Important for solving problems related to surface area
Circle	π × Radius²	2 × π × Radius	Remember to use the value of π as 3.14 or 22/7 for approximations
Triangle	1/2 × Base × Height	Sum of the lengths of all three sides	Pay attention to different types of triangles (e.g., equilateral, right)
Circle (Volume of Cylinder)	π × Radius² × Height	N/A	Use for 3D problems involving cylinders

Tips for Solving Geometry Problems

When tackling geometry problems, always follow these steps:

• Identify the shape: Recognize the geometric figure in the problem and note its key features (e.g., radius, sides, angles).
• Apply the correct formulas: Use the appropriate area, perimeter, or volume formulas for the shape in question.
• Check for special properties: For certain shapes (e.g., right triangles, circles), special rules or theorems like the Pythagorean theorem or properties of angles may apply.
• Draw the figure: Sketching the figure can help visualize the problem and clarify the relationships between different elements.

By understanding these fundamental concepts and applying the appropriate formulas, you will be better equipped to tackle geometry problems with confidence.

Mastering Linear Functions and Graphs

Understanding linear functions and how to graph them is essential for solving a wide range of problems. A linear function describes a straight line when plotted on a coordinate plane, and its properties can be used to model real-world situations. In this section, we will explore the core concepts related to linear functions, how to graph them, and how to interpret the information they provide.

Key Concepts of Linear Functions

To fully grasp linear functions, it’s important to understand their components and how they behave:

• Slope: The slope represents the rate of change between two points on a line. It is calculated as the change in y-values divided by the change in x-values.
• Y-Intercept: This is the point where the line crosses the y-axis. It represents the value of the dependent variable when the independent variable is zero.
• Equation of a Line: The general form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.
• Graphing a Line: Plotting a linear equation involves finding two or more points on the line and connecting them. The slope helps determine the direction of the line, while the y-intercept indicates where the line crosses the y-axis.

Steps to Graph a Linear Function

Follow these steps to graph a linear function successfully:

1. Identify the slope and y-intercept: From the equation of the line, find the values of m (slope) and b (y-intercept).
2. Plot the y-intercept: Begin by marking the point (0, b) on the graph, which represents the y-intercept.
3. Use the slope to find another point: From the y-intercept, use the slope to find another point on the line. For example, if the slope is 2, move 2 units up and 1 unit to the right to find the next point.
4. Draw the line: Once you have at least two points, draw a straight line through them. This is the graph of the linear function.

By mastering these steps and understanding the key concepts, you can easily graph any linear function and interpret its meaning in various contexts.

Tips for Tackling Word Problems

Word problems can be some of the most challenging questions, as they require you to translate written information into mathematical concepts. The key to solving them is to break down the problem into manageable parts, identify what is being asked, and apply the correct mathematical operations. In this section, we will provide some useful strategies to help you approach and solve word problems with confidence.

Step-by-Step Approach

Following a structured method can make even the most complex word problems easier to handle. Here are some steps to guide you:

• Read the problem carefully: Make sure to read the problem several times to fully understand the context and what is being asked.
• Identify key information: Highlight or underline important numbers, variables, and relationships within the text.
• Set up equations: Once you’ve identified the necessary information, translate it into an equation or a system of equations.
• Define variables: Assign a letter or symbol to represent unknown quantities. Clearly define what each variable stands for.
• Solve the equation: Use appropriate mathematical operations to solve for the unknown value(s). Be sure to check your work at each step.
• Answer the question: Once you have solved the equation, make sure your solution answers the specific question asked in the problem.

Common Word Problem Types

Word problems can come in many forms, but here are a few common types that you might encounter:

• Proportions: These problems involve relationships between two or more quantities, often requiring you to set up a proportion and solve for an unknown value.
• Rates: Problems involving speed, distance, time, or work are solved by using rate formulas, like Distance = Rate × Time.
• Age problems: These problems typically involve setting up equations based on the difference in ages between two or more people.
• Mixture problems: These involve mixing different quantities (like liquids or solids) and finding the resulting mixture’s properties.

By practicing these steps and becoming familiar with common problem types, you can significantly improve your ability to solve word problems efficiently and accurately.

Probability and Statistics Review

Understanding the principles of chance and data analysis is essential for solving problems in a variety of contexts. Probability and statistics allow us to make informed predictions and decisions based on data. In this section, we will review the key concepts in probability and statistics, including how to calculate the likelihood of events and analyze data sets to draw meaningful conclusions.

Key Concepts in Probability

Probability is the study of the likelihood of events occurring. Some fundamental concepts include:

• Probability of an Event: The probability of an event is a number between 0 and 1 that represents how likely an event is to occur. It is calculated as the ratio of favorable outcomes to the total number of possible outcomes.
• Complementary Events: The probability that an event does not occur is called the complement. The sum of the probability of an event and its complement is always 1.
• Independent and Dependent Events: Independent events do not affect each other’s probability, while dependent events are influenced by prior outcomes.
• Compound Events: These involve the combination of two or more events. The probability of compound events can be calculated using the addition or multiplication rules.

Key Concepts in Statistics

Statistics involves the collection, organization, and interpretation of data. Some important statistical concepts are:

• Mean: The mean is the average value of a data set, calculated by summing all values and dividing by the number of data points.
• Median: The median is the middle value in a sorted data set. If there is an even number of data points, the median is the average of the two middle values.
• Mode: The mode is the value that appears most frequently in a data set.
• Standard Deviation: Standard deviation measures the spread of data points around the mean. A smaller standard deviation indicates that the data points are closer to the mean, while a larger standard deviation indicates more variability.
• Probability Distributions: A probability distribution is a function that describes the likelihood of different outcomes in a random experiment. Common distributions include the normal distribution and binomial distribution.

Mastering these key concepts in probability and statistics will help you solve a wide variety of problems and make data-driven decisions in both academic and real-world scenarios.

Polynomials and Factoring Explained

Polynomials are algebraic expressions consisting of variables and coefficients, combined using addition, subtraction, and multiplication. Understanding how to manipulate these expressions and break them down into simpler forms is crucial for solving complex problems. Factoring is a key technique for simplifying polynomials, which involves expressing them as the product of simpler binomials or monomials. In this section, we will explore how to work with polynomials and the methods for factoring them.

What is a Polynomial?

A polynomial is an expression made up of terms, each containing a variable raised to a power and multiplied by a coefficient. Polynomials can have one or more terms, and they can be classified based on the number of terms they contain:

• Monomial: A polynomial with only one term (e.g., 3x or 5).
• Binomial: A polynomial with two terms (e.g., x + 5 or 2x – 3).
• Trinomial: A polynomial with three terms (e.g., x^2 + 5x + 6).
• Multinomial: A polynomial with more than three terms (e.g., x^3 + 2x^2 + 3x – 4).

The degree of a polynomial is determined by the highest power of the variable present in the expression. For example, the polynomial 4x^3 + 2x^2 – 5x + 1 has a degree of 3 because the highest exponent of the variable x is 3.

Factoring Polynomials

Factoring is the process of expressing a polynomial as the product of simpler polynomials. This technique is used to simplify expressions, solve equations, and find the roots of a polynomial. There are several methods for factoring polynomials, including:

• Factoring out the Greatest Common Factor (GCF): Start by identifying the greatest common factor of all the terms and factor it out. For example, in 6x^2 + 9x, the GCF is 3x, so the factored form is 3x(2x + 3).
• Factoring by Grouping: Group terms in pairs, factor out the GCF from each pair, and then factor out the common binomial factor. This method works best when the polynomial has four terms.
• Factoring Trinomials: For quadratics of the form ax^2 + bx + c, look for two numbers that multiply to ac and add to b. Then, rewrite the middle term using these two numbers and factor by grouping.
• Difference of Squares: This is a special case where the polynomial is the difference between two perfect squares, such as a^2 – b^2. It factors as (a – b)(a + b).

Mastering the process of factoring polynomials is essential for simplifying complex expressions and solving algebraic equations. With practice, you can quickly recognize which method to apply based on the structure of the polynomial.

Trigonometry Basics for the Exam

Trigonometry plays a significant role in many problems involving angles and distances. Understanding the foundational principles of trigonometric functions and their applications can simplify solving geometric and algebraic problems. This section covers the essential concepts and methods you need to know for tackling trigonometry-related questions.

Key Trigonometric Functions

The three main trigonometric functions used in most problems are sine, cosine, and tangent. These functions relate the angles of a right triangle to the ratios of its sides. Here’s a quick overview of each function:

• Sine (sin): The ratio of the length of the opposite side to the hypotenuse. sin(θ) = opposite / hypotenuse.
• Cosine (cos): The ratio of the length of the adjacent side to the hypotenuse. cos(θ) = adjacent / hypotenuse.
• Tangent (tan): The ratio of the length of the opposite side to the adjacent side. tan(θ) = opposite / adjacent.

These functions can be used to solve for unknown sides or angles in right triangles, which is the foundation of most trigonometry problems.

Trigonometric Identities

Trigonometric identities are essential tools for simplifying expressions and solving equations. Here are a few key identities you should remember:

• Pythagorean Identity: sin²(θ) + cos²(θ) = 1
• Reciprocal Identities: csc(θ) = 1/sin(θ), sec(θ) = 1/cos(θ), cot(θ) = 1/tan(θ)
• Quotient Identity: tan(θ) = sin(θ) / cos(θ)

Using these identities allows you to simplify complex trigonometric expressions and solve problems more efficiently.

Understanding the Unit Circle

The unit circle is another key concept in trigonometry. It helps visualize the relationship between angles and the values of trigonometric functions. The unit circle is a circle with a radius of one unit centered at the origin of the coordinate plane. By knowing the coordinates on the unit circle, you can quickly determine the values of sine and cosine for any angle.

It’s important to be familiar with the key angles on the unit circle, such as 30°, 45°, and 60°, and their corresponding sine and cosine values. Memorizing these will help you solve problems more quickly without relying on a calculator.

Solving Trigonometric Problems

When solving trigonometry problems, start by identifying which sides and angles are involved. If you are working with a right triangle, use the appropriate trigonometric function (sine, cosine, or tangent) to relate the sides and angles. If the problem involves the unit circle or identities, simplify the expression using known values and relationships.

By understanding these basics and practicing regularly, you’ll be well-prepared for any trigonometry questions that come your way.

Time Management During the Exam

Effective time management is crucial when tackling any test, especially one that involves a variety of problem types. The key to success is knowing how to allocate your time efficiently so you can answer as many questions as possible without feeling rushed. By planning ahead and following a structured approach, you can maximize your performance and reduce stress.

Prioritize Your Questions

When you first receive the test, take a few moments to scan through all the questions. Identify the ones that seem easiest or that you can solve quickly. By addressing these first, you will build confidence and free up more time for the more challenging problems later. It’s important to answer the easier questions first and avoid getting stuck on difficult ones.

Allocate Time for Each Section

Most tests are divided into sections, each with a different type of question. For example, one section may focus on algebra, while another covers geometry or word problems. Before you start working, set a time limit for each section based on the number of questions and the amount of time available. If you find yourself spending too much time on one section, move on and come back to it later if you have time left at the end.

• Set specific time limits: Break the overall test duration into manageable blocks for each section.
• Track your progress: Keep an eye on the clock to ensure you’re staying on schedule.
• Don’t linger too long: If you get stuck, skip to the next question and come back later.

Practice Mental and Physical Stamina

Tests can be mentally exhausting, especially when they are lengthy. To avoid burnout, practice pacing yourself during study sessions. When working on practice tests, simulate the time pressure you will face during the actual test. This will help you build stamina and learn how to maintain focus under pressure. Additionally, take brief breaks during study sessions to refresh your mind, but avoid distractions that might derail your focus.

Review and Adjust as Needed

Once you’ve completed all the questions you can easily answer, return to the more difficult ones. Use any remaining time to double-check your work and adjust any answers that you may have rushed through. Don’t waste the last few minutes–make sure you’ve reviewed your responses for any errors or missed steps.

By staying calm, managing your time effectively, and keeping a clear focus, you can approach the test with confidence and improve your chances of success.

Common Mistakes to Avoid

During any test, it’s easy to make mistakes, especially when under time pressure or dealing with complex problems. However, recognizing and avoiding common pitfalls can significantly improve your performance. By staying focused and following a systematic approach, you can minimize errors and maximize your score.

Rushing Through Questions

One of the most common mistakes is rushing through questions in an attempt to finish quickly. While time management is important, it’s crucial to read each question carefully and fully understand what is being asked. Skipping key details or misinterpreting the problem can lead to incorrect answers. Always take the time to review the question before jumping into the solution.

Neglecting to Check Your Work

Another frequent error is failing to review your answers before submitting the test. Many students overlook simple mistakes, such as arithmetic errors or misread questions, that can be easily corrected with a quick review. Make sure to leave some time at the end to go over your work. Double-check calculations and ensure that you’ve answered every question.

Misunderstanding the Instructions

Sometimes students overlook important instructions that could affect how they approach a problem. For instance, some questions might have specific formatting requirements, or there may be restrictions on how to show your work. Always read the instructions thoroughly before beginning each section to ensure you’re following the proper guidelines.

Skipping Harder Questions

While it’s important to manage your time efficiently, skipping difficult questions entirely can be a costly mistake. If a question seems too challenging at first, try to break it down into smaller, more manageable parts or estimate an answer. Leaving it blank will only hurt your chances of scoring, so attempt every question–even if it’s just a rough solution that you can refine later.

Not Using All Available Resources

If the test allows the use of tools such as a calculator, scratch paper, or reference sheets, make sure to use them. Some students forget to utilize these resources, even though they can make a significant difference in solving problems more efficiently. Don’t hesitate to make full use of everything available to you to ensure accurate and timely solutions.

By avoiding these common mistakes and staying calm under pressure, you can approach the test with confidence and improve your performance. Remember that careful preparation and attention to detail are key to achieving success.

Strategies for Multiple-Choice Questions

Multiple-choice questions can often seem straightforward, but they require careful strategy to answer correctly. These types of questions test your understanding and ability to make quick decisions under pressure. Developing effective strategies will help you maximize your performance and increase your chances of choosing the correct option.

Eliminate Incorrect Answers

One of the most effective strategies is to eliminate obviously wrong answers first. This increases your chances of selecting the right option, even if you’re unsure about the correct answer. Look for extreme answers, contradictions, or options that don’t make sense based on your knowledge.

Read All the Choices Carefully

Even if one answer seems correct at first glance, it’s important to read all the options thoroughly. Sometimes, there are answers that are very similar, with only a small difference. Make sure to evaluate each choice carefully before making your final selection.

Look for Clues in the Question

Sometimes, the question itself can provide valuable hints that point you towards the correct answer. Pay attention to wording that can suggest relationships, patterns, or calculations. Words like “always,” “never,” “most likely,” or “least likely” can indicate the type of answer you should look for.

Use Logical Reasoning

If you are unsure about an answer, use logical reasoning to eliminate choices that don’t fit. Think about the context of the problem and use your basic knowledge to narrow down the possibilities. Often, there are only one or two options that seem logically consistent with the information provided.

Skip and Return to Difficult Questions

If you encounter a particularly tricky question, don’t waste too much time on it. Mark it and move on to the next one. Once you’ve completed the rest of the test, you can return to the challenging question with a fresh perspective, which might help you identify the correct answer.

Guess If Necessary

If you’ve narrowed down the options but still aren’t sure about the correct answer, make an educated guess. Studies show that guessing when you have some idea about the answer is better than leaving the question blank. Even if you can’t be sure, making a guess gives you a chance to score points.

• Eliminate obviously wrong answers
• Read all the options carefully
• Look for clues in the question
• Use logical reasoning to narrow choices
• Skip difficult questions and return to them later
• Make an educated guess if necessary

By employing these strategies, you can improve your efficiency and accuracy in answering multiple-choice questions. Remember, practice is key–familiarity with the test format and the types of questions asked will help you make better decisions under pressure.

How to Check Your Final Exam Answers

Reviewing your responses before submitting any test is a crucial step to ensure accuracy and avoid careless mistakes. Effective checking can be the difference between a good and great score. Here are some strategies to help you evaluate your work thoroughly and efficiently.

Step-by-Step Review Process

When checking your work, follow a systematic approach to ensure you don’t miss any errors. Start by reviewing each question and answer methodically. It’s also helpful to review the instructions for each section, as some problems may require specific formats or steps.

Common Mistakes to Look For

While checking, pay attention to these frequent errors that can slip past during the initial test-taking process:

• Calculation errors: Double-check your arithmetic, as simple mistakes in addition, subtraction, multiplication, or division can lead to incorrect results.
• Misinterpreting the question: Sometimes, in the rush to finish, it’s easy to misread or misunderstand the question’s requirements.
• Omitting units or labels: Always include necessary units (like inches, meters, or dollars) and labels for clarity.
• Skipping a step: If you are solving a problem in multiple steps, make sure all steps are included and logically ordered.

Use a Checklist for Verification

A checklist can help you stay organized when reviewing. You can quickly confirm if you’ve covered all aspects of each problem. Consider the following example:

Step	Checklist Item	Status
1	Read the question carefully	✔️
2	Check calculations for accuracy	✔️
3	Verify units and labels are included	❌
4	Ensure all steps are shown in the solution	✔️
5	Review answers for logical consistency	✔️

Take Your Time and Stay Focused

While time may be limited, try to reserve the last 10–15 minutes of your testing period for checking. Avoid rushing through the final review, as this can lead to missing simple mistakes. Staying calm and focused can help you spot errors more effectively.

In summary, checking your work thoroughly can help identify small mistakes that can add up. By using a systematic approach and staying vigilant for common errors, you can significantly improve the accuracy of your responses.

Resources for Further Study

Building a strong foundation in various topics requires not only classroom learning but also self-study and external resources. Whether you’re looking to strengthen your skills or explore more advanced concepts, numerous tools and materials can help you succeed. Below are some valuable resources that can support your ongoing learning journey.

Online Learning Platforms

Many websites offer structured lessons, exercises, and video tutorials to enhance your understanding. Here are a few you might find useful:

• Khan Academy: Provides free, high-quality videos and practice exercises on a wide range of subjects, from basic concepts to more advanced topics.
• Coursera: Offers online courses from top universities. Some courses are free, while others may require a fee or subscription.
• EdX: Features a variety of courses from universities and institutions worldwide. You can find both free and paid options.

Textbooks and Study Guides

Books and study guides provide in-depth explanations and practice problems. Consider exploring these resources:

• Study guides: Many publishers offer specialized guides for different topics. Look for study materials tailored to the subject areas you’re studying.
• Textbooks: Traditional textbooks often break down complex topics into manageable sections, with examples and exercises for practice.
• Practice Workbooks: Books filled with practice problems and solutions help reinforce learning and build problem-solving skills.

Interactive Tools and Apps

Interactive apps and tools allow for hands-on practice in an engaging way. Here are some useful suggestions:

• Wolfram Alpha: A powerful tool for solving equations, graphing functions, and exploring data in various subjects.
• GeoGebra: An interactive geometry, algebra, and calculus application that helps visualize mathematical concepts.
• Desmos: A graphing calculator tool that allows you to explore and analyze different types of graphs and functions.

Tutoring and Study Groups

If you’re struggling with specific topics, tutoring can provide personalized assistance. Look for:

• Online Tutoring Services: Websites like Chegg Tutors or Tutor.com offer one-on-one support with qualified instructors.
• Study Groups: Forming or joining a study group with classmates can help you understand different approaches to solving problems and share knowledge.

Utilizing a combination of these resources will provide a well-rounded approach to mastering the material. Regular practice, self-assessment, and seeking help when necessary are key to reinforcing your understanding and excelling in your studies.