
When it comes to preparing for an important test, effective strategies and thorough understanding are key to performing well. Whether you’re tackling complex problems or refining your problem-solving skills, the right approach can make all the difference. This section will guide you through essential tips and techniques to ensure you’re well-prepared for the challenges ahead.
From mastering core concepts to practicing essential skills, it’s important to approach your review systematically. Focusing on the areas that require the most attention while also strengthening your existing knowledge can help you stay confident and organized. Effective study habits, combined with strategic planning, can significantly boost your chances of success.
In this guide, you’ll find expert advice on preparing for your test, including methods for tackling difficult questions, optimizing time management, and using resources to aid your review. With the right mindset and preparation, you’ll be ready to tackle any challenge that comes your way.
Test Preparation Strategies and Solutions
Success on any assessment relies on understanding key concepts, applying problem-solving techniques, and practicing effectively. Whether you’re faced with complex calculations or theoretical questions, the right preparation can help you approach each challenge with confidence. This section highlights essential strategies to help you perform your best when it matters most.
Mastering Problem-Solving Techniques
One of the most important aspects of performing well is developing a clear and systematic approach to solving problems. It’s not just about getting the correct result but understanding the process that leads to it. Focus on building a strong foundation in critical thinking and step-by-step solutions that will guide you through any task. Practice with diverse problem sets to improve both speed and accuracy.
Effective Time Management During Assessments
Efficient time management is crucial for maximizing your performance under pressure. Prioritize questions based on their difficulty and allocated time. Start with simpler tasks to build momentum, leaving more challenging ones for later. By allocating time wisely, you can ensure that each part of the test receives the attention it needs, without running out of time.
Effective Study Strategies for Success
Preparing for an important assessment requires more than just reviewing notes. To truly excel, it’s essential to develop a strategic approach that focuses on both understanding the material and applying it effectively. A well-organized study plan will ensure that you cover all necessary topics and build confidence in your ability to solve problems efficiently.
Structured Review Plan

Start by breaking down the content into manageable sections. Create a study schedule that allocates time to each topic based on its complexity and your familiarity with it. This helps you avoid last-minute cramming and ensures a thorough understanding of each concept. Aim to review regularly, reinforcing key points through repetition and practice.
Active Practice and Application
Merely reading through your materials isn’t enough. Engage with the content actively by working through practice problems, as this helps reinforce your learning. Focus on applying concepts to a variety of problems, from basic to more complex scenarios. Problem-solving practice sharpens your skills and prepares you for the variety of questions that may appear on the assessment.
Common Topics on Assessments
Understanding the key areas that frequently appear on important evaluations is essential for efficient preparation. Certain topics often form the foundation of the assessment, and being familiar with them can provide a significant advantage. These areas require in-depth study to ensure you can approach each question confidently and effectively.
Essential Topics to Review

The following subjects are commonly tested and should be given priority during your study sessions:
- Algebraic Manipulations
- Problem-Solving Techniques
- Functions and Graphs
- Basic Calculus Concepts
- Systems of Equations
- Matrix Operations
Key Areas for Advanced Problem Solving
In addition to fundamental concepts, these advanced topics are often explored in-depth:
- Integral and Derivative Applications
- Complex Word Problems
- Optimization and Rate of Change
- Probability and Statistics
- Logarithmic and Exponential Functions
Understanding Key Formulas for Success
Mastering the essential formulas is critical for achieving success in any assessment. These formulas serve as the foundation for solving a wide range of problems efficiently. Having a solid grasp of key mathematical expressions allows you to quickly identify the appropriate approach and apply it to various questions, saving valuable time during the evaluation.
Important Mathematical Formulas
Familiarity with these commonly used formulas will help you tackle many different types of problems:
- Quadratic Formula: For solving quadratic equations
- Distance Formula: To calculate the distance between two points
- Pythagorean Theorem: Essential for right-angled triangle problems
- Area and Volume Formulas: Key for geometry-related questions
- Derivative and Integral Rules: Important for calculus applications
Tips for Memorizing and Applying Formulas
Understanding how and when to use these formulas is just as important as memorizing them. Regular practice and real-world applications will help reinforce your knowledge. Focus on solving a variety of problems to understand the context in which each formula should be used. Additionally, creating a formula sheet and reviewing it consistently will make recalling important equations easier during the assessment.
How to Approach Word Problems
Word problems can often seem daunting, as they require both analytical thinking and the ability to translate real-world situations into mathematical expressions. The key to solving these problems is breaking them down step by step and identifying the relevant information. By following a systematic approach, you can solve even the most complex problems with confidence.
Step-by-Step Approach

To tackle word problems efficiently, follow these steps:
- Read the problem carefully: Understand what is being asked before attempting to solve it.
- Identify known and unknown values: Highlight key information and what needs to be found.
- Translate the words into equations: Convert the narrative into mathematical terms and expressions.
- Set up a strategy: Choose the most appropriate method or formula to solve the problem.
- Check your work: Review the solution to ensure all conditions are met and the answer makes sense.
Tips for Success
Here are some additional strategies to help you succeed with word problems:
- Practice regularly to build familiarity with different types of word problems.
- Draw diagrams or graphs when appropriate to visualize the problem.
- Break the problem into smaller parts and solve each one sequentially.
- Don’t rush – take your time to fully understand the problem before solving it.
Time Management Tips for Assessments
Effective time management is crucial when preparing for any test. Properly allocating your time during the assessment ensures that you can complete all tasks without feeling rushed. With a strategic approach, you can optimize your performance by focusing on the most important questions and avoiding unnecessary stress.
Prioritizing Questions
Start by assessing the difficulty of each question. Tackle the easier problems first to build confidence and gain momentum. Once the simpler questions are completed, move on to more complex problems. This approach helps you manage your time efficiently and ensures that you don’t spend too long on any single task.
Time Allocation Strategy
Divide the total time available for the assessment by the number of questions to determine how much time you should allocate to each one. Adjust this allocation based on the difficulty and length of the questions. Be mindful of the clock and stick to your plan to ensure you complete all sections within the allotted time.
Practice Problems for Better Preparation

Regular practice is one of the most effective ways to reinforce your understanding and improve your problem-solving abilities. By solving a variety of problems, you become more familiar with different types of questions and develop strategies to approach them with confidence. The more problems you practice, the more comfortable you will feel when facing similar challenges during the assessment.
Focus on a wide range of problems, from basic concepts to more complex scenarios. This not only strengthens your foundation but also helps you adapt to various problem formats. Consider working through practice sets, using textbooks or online resources, and reviewing past tasks to ensure you’re fully prepared for the upcoming test.
Test-Taking Tips for Success
Effective test-taking strategies are just as important as thorough preparation. During the assessment, staying calm and organized can help you maximize your performance. Having a clear approach for tackling questions allows you to navigate through the test efficiently and avoid unnecessary stress.
One key tip is to read each question carefully before starting. This ensures you understand exactly what is being asked and helps prevent mistakes. Additionally, managing your time well throughout the test is essential. Start with the easier questions to build confidence and ensure you allocate enough time for the more difficult ones.
Mastering Algebra for Success
Algebra forms the foundation of many mathematical concepts and is often a key area of focus in any assessment. Understanding algebraic principles is crucial for solving a wide range of problems efficiently. By mastering this subject, you will gain the skills needed to approach both basic and advanced questions with confidence.
Key Algebraic Concepts to Master
To excel in algebra, it is important to be familiar with the following concepts:
- Solving linear and quadratic equations
- Understanding functions and their graphs
- Factoring polynomials and expressions
- Manipulating exponents and radicals
- Working with inequalities and systems of equations
Practice Techniques for Mastery
Regular practice is the key to mastering algebra. Focus on solving a variety of problems to build a strong foundation. Break down complex problems into smaller steps to understand the process more clearly. Additionally, reviewing mistakes and learning from them can help you identify areas for improvement and boost your problem-solving skills.
Tips for Tackling Calculus Questions
Calculus questions can often appear challenging due to their abstract nature and intricate concepts. However, with the right approach and a solid understanding of key principles, these problems become manageable. A strategic approach to these questions helps you break down complex topics and apply the necessary techniques effectively to reach the correct solutions.
Important Concepts to Focus On
To tackle calculus problems confidently, it’s essential to understand and practice the following concepts:
| Concept | Description |
|---|---|
| Limits | Understanding how functions behave as they approach certain points. |
| Derivatives | Calculating the rate of change of a function with respect to a variable. |
| Integrals | Finding the accumulated area under a curve, useful in a variety of applications. |
| Chain Rule | A technique for differentiating composite functions. |
| Fundamental Theorem of Calculus | Connecting derivatives and integrals, allowing for the evaluation of integrals using antiderivatives. |
Strategies for Solving Calculus Problems
When approaching calculus questions, keep the following tips in mind:
- Read the problem carefully: Identify key information and determine which concept applies.
- Simplify the problem: Break down complex problems into simpler parts to make the solution more manageable.
- Check for known formulas: Many problems can be solved directly with the appropriate formulas or theorems, so be sure to recognize them.
- Practice derivatives and integrals: Being comfortable with differentiating and integrating functions is essential for success.
How to Use a Calculator Efficiently
Using a calculator effectively can save you valuable time and reduce the risk of making errors during problem-solving. With the right techniques, you can streamline your calculations and ensure accuracy throughout your work. Whether performing basic arithmetic or solving complex equations, understanding how to leverage your calculator’s features is essential for optimal performance.
Maximizing Calculator Features
To get the most out of your calculator, focus on these key functions:
- Memory functions: Utilize the memory keys to store intermediate results, so you don’t need to re-enter values multiple times.
- Parentheses: Properly using parentheses ensures the correct order of operations, especially in complex calculations.
- Scientific functions: Get comfortable with advanced features like square roots, exponents, and trigonometric functions to handle a wide range of problems.
- Clear errors quickly: Familiarize yourself with the “clear” or “undo” buttons to avoid mistakes that can throw off your calculations.
Tips for Efficient Use During Tests
Here are some practical tips to help you use your calculator effectively during the test:
- Familiarize yourself: Practice using your calculator before the test so you can easily access its functions under pressure.
- Plan your calculations: Break down complex problems into smaller steps and enter the calculations sequentially to avoid mistakes.
- Double-check results: Always verify your answer by recalculating key steps to ensure consistency and accuracy.
- Don’t rely on the calculator for everything: Use mental math or paper for simple operations to save time for more complex tasks.
Key Concepts to Focus On
When preparing for any assessment involving advanced problem-solving, it’s essential to focus on mastering core concepts that frequently appear in questions. Strengthening your understanding of these fundamental topics allows you to approach a wide range of problems with greater ease and confidence. These concepts are foundational to more complex ideas, making them critical for success.
Core Areas to Review
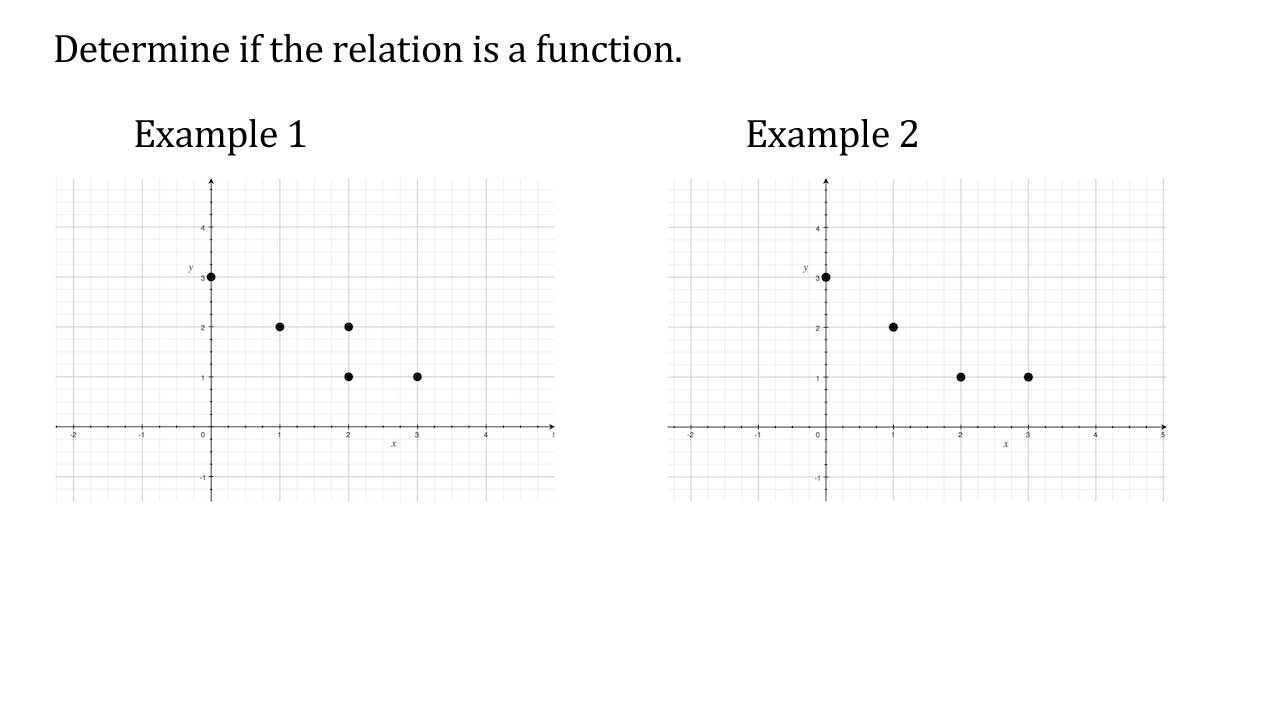
To help structure your preparation, focus on the following key areas:
| Concept | Description |
|---|---|
| Functions | Understanding how different types of functions behave and how to manipulate them. |
| Derivatives | Grasping the concept of rates of change and how to compute derivatives for various types of functions. |
| Integrals | Focusing on methods to find areas under curves and solving problems involving integration. |
| Algebraic Manipulations | Mastering techniques like factoring, simplifying, and solving equations algebraically. |
| Trigonometry | Strengthening your understanding of angles, sine, cosine, and other trigonometric identities. |
Techniques for Effective Mastery
Focusing on the right concepts is only part of the process. To ensure mastery, practice regularly, work through various problem types, and continuously test your understanding of each concept. The more time spent engaging with these fundamental topics, the easier it becomes to tackle more complex questions with confidence.
Understanding Graphing for Exams
Graphing is a powerful tool in problem-solving that can provide visual clarity to complex mathematical relationships. Whether dealing with functions, inequalities, or data sets, knowing how to plot and interpret graphs accurately is essential for demonstrating your understanding. The ability to read graphs and plot points correctly can often be the difference between correctly solving a problem and missing key details.
In preparation for any test, it is important to practice graphing a variety of functions and interpreting the key features of each. This involves understanding the relationship between the equation and its graphical representation, as well as the implications of changes in coefficients and constants. Mastering graphing techniques allows you to visualize problems more effectively and solve them with greater accuracy.
While graphing by hand is a useful skill, familiarity with graphing tools or calculator functions that plot graphs can help save time and reduce errors. Whether you’re graphing linear equations, quadratic functions, or trigonometric curves, the key is to focus on plotting key points, identifying intercepts, and analyzing key features such as slope, curvature, and asymptotes.
Common Mistakes to Avoid
During any assessment, it’s easy to make mistakes that could cost valuable points. Many of these errors are avoidable with proper preparation and careful attention to detail. Recognizing common pitfalls helps ensure you don’t lose marks on simple mistakes, which could otherwise be easily fixed with a little more focus.
One common mistake is rushing through problems without reading the instructions carefully. Often, students overlook key details or misinterpret what the question is asking. Taking a moment to thoroughly understand each problem before diving into calculations can help avoid such errors.
Another frequent issue is misapplying formulas or using incorrect methods. It’s crucial to understand the underlying principles behind each formula and to be certain you’re applying the right approach to each specific problem. Double-checking calculations can also prevent errors caused by simple arithmetic mistakes or overlooked steps.
Finally, failing to check your answers is a mistake many make, even after completing a problem. After working through a solution, it’s important to review your work, ensuring all steps are correct and that your final answer makes sense in the context of the question. This last step can help catch small, easily avoidable errors.
Utilizing Online Resources for Help
In today’s digital age, a wealth of online resources is available to assist students in understanding complex concepts and solving challenging problems. Whether you need step-by-step explanations, practice questions, or video tutorials, the internet offers a variety of tools that can help enhance your understanding and improve your skills.
Websites and platforms such as educational forums, interactive problem solvers, and video tutorials are valuable assets when studying. These resources can provide alternative explanations and approaches that might resonate better with your learning style. By exploring different perspectives, you can deepen your comprehension and tackle problems more effectively.
Additionally, many online tools allow you to practice problems and get immediate feedback. This instant review helps reinforce learning and allows you to track progress over time. Engaging with online study groups or communities can also be beneficial, as discussing topics with peers can clarify doubts and offer new insights.
How to Handle Test Anxiety
Test-related stress is a common experience for many students, but it is possible to manage this anxiety and perform to the best of your abilities. Understanding the factors that contribute to stress, along with strategies to cope, can help you stay calm and focused during assessments.
One key approach is preparation. Adequate studying and review not only improve your knowledge but also increase your confidence. When you feel well-prepared, you are less likely to feel overwhelmed when faced with challenging questions. Break your study sessions into manageable chunks, and give yourself enough time to review all key material.
Relaxation techniques can also be helpful. Breathing exercises, mindfulness, and even physical activity can reduce tension and clear your mind. Taking short breaks while studying and ensuring you get enough rest before the assessment can keep you sharp and reduce feelings of panic.
| Tip | Description |
|---|---|
| Practice Relaxation Techniques | Try deep breathing, meditation, or yoga to stay calm before and during the test. |
| Manage Your Time | Plan your study schedule in advance to avoid last-minute cramming. |
| Visualize Success | Imagine yourself calmly completing the assessment and achieving your goals. |
Finally, remember that test results do not define you. Having a healthy mindset, where you focus on doing your best without excessive pressure, can greatly enhance your performance. Recognize that it’s okay to feel nervous, but with the right tools, you can overcome the anxiety and tackle any assessment confidently.
Reviewing Past Exams for Practice
One of the most effective ways to prepare for any assessment is by reviewing previous tests. This method not only helps reinforce key concepts but also familiarizes you with the format and types of questions that are commonly asked. By revisiting past materials, you can identify areas of weakness and strengthen your understanding.
When reviewing past assessments, focus on the following strategies:
- Identify Common Topics: Look for recurring themes or types of questions. This can help you focus your preparation on areas that are likely to appear again.
- Understand Mistakes: Review your errors from previous attempts and make sure you understand why they occurred. This will prevent similar mistakes from happening in the future.
- Simulate Test Conditions: Try completing past tests within the time limit, just as you would in the actual assessment. This will help you practice time management and build confidence.
In addition to practicing with old tests, consider these tips to make your review even more effective:
- Organize Your Review: Break your study into specific sections, such as focusing on one topic or question type at a time.
- Use Multiple Resources: Combine your review with additional study materials such as textbooks, online tutorials, or study groups to reinforce your understanding.
- Track Your Progress: As you work through past assessments, keep track of which areas still need improvement and review them more thoroughly.
By consistently reviewing past assessments and practicing with real-world problems, you can sharpen your problem-solving skills and feel more prepared when it comes time for the real challenge.
Improving Accuracy in Problem Solving
Achieving precision in solving problems is essential for success in any assessment. Small mistakes can add up, leading to incorrect results. Focusing on accuracy not only improves performance but also helps build confidence when approaching complex tasks. To enhance your ability to solve problems correctly, it’s important to adopt effective strategies and practice consistently.
Here are several key strategies to improve your accuracy when solving problems:
- Double-Check Your Work: After completing a problem, take a moment to review your calculations and the steps you followed. This simple habit can help you catch errors that might have been overlooked during the initial process.
- Break Problems Into Smaller Steps: Instead of jumping straight to the solution, break down each problem into manageable parts. This helps to reduce mistakes and ensures that each step is correct before moving on.
- Use Logical Reasoning: Approach each problem methodically. Ensure you understand the underlying principles and use them as a guide throughout the problem-solving process.
- Minimize Distractions: Create an environment conducive to focus. Eliminate distractions and work in a quiet, comfortable space to enhance concentration and reduce the likelihood of errors.
Additionally, consistent practice plays a vital role in accuracy improvement. The more problems you solve, the more familiar you become with common patterns and techniques, which makes you less prone to errors over time.