Math U See Algebra 1 Answers and Solutions Guide

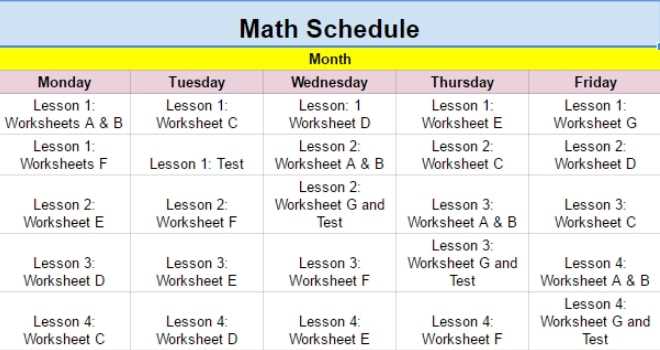
In this section, we will guide you through the process of solving mathematical problems typically encountered at the foundational level. Whether you’re looking for strategies to tackle equations or insights into complex problem-solving techniques, this resource will provide the clarity you need.

By breaking down key principles and offering step-by-step explanations, we aim to help students grasp essential skills. The focus is on fostering a deep understanding of core concepts, enabling learners to build confidence and solve problems with ease.

Practical exercises and targeted strategies will ensure that you’re prepared for various types of challenges. This approach helps simplify complex topics, turning them into manageable and approachable tasks for learners at any level.

Through consistent practice and clear guidance, you will find yourself mastering the fundamentals, setting the stage for more advanced mathematical pursuits in the future.

Math U See Algebra 1 Answers

In this section, we will explore how to approach and solve key problems typically found in introductory mathematics courses. By focusing on essential techniques and providing clear solutions, this guide aims to assist students in strengthening their understanding and problem-solving abilities. Each concept is broken down to ensure accessibility and clarity, helping learners gain confidence in their skills.

Mastering Core Problem-Solving Skills

Understanding the fundamentals is crucial when solving mathematical equations and expressions. This section walks you through various examples, offering clear steps for each type of problem. From solving simple linear equations to more complex expressions, we provide all the tools needed to tackle different types of exercises. By following these methods, students can better retain and apply the material to future challenges.

Building Confidence Through Practice

Regular practice is essential for mastering any new skill. By continually working through similar problems, students can reinforce their understanding and build proficiency. Each example provided in this section encourages consistent application of the learned concepts, allowing for incremental growth in solving more advanced problems. With focused effort and the right resources, learners will be equipped to handle even the toughest questions with ease.

Understanding Math U See Method

The approach used in this program focuses on building a strong foundation through step-by-step instruction. It emphasizes clarity and comprehension, helping students to understand concepts progressively. The method involves breaking down complex topics into smaller, more manageable parts, allowing learners to gain a deeper understanding before moving on to more advanced material.

Hands-on practice plays a critical role in this method. By working through numerous examples and exercises, students are encouraged to actively engage with the material. This approach fosters retention and makes it easier to apply learned concepts in real-world situations. With a focus on gradual mastery, learners can build confidence and develop a solid grasp of essential skills.

Through repetition and focused learning, this method offers a comprehensive way to tackle mathematical challenges. The aim is to ensure that students not only memorize formulas but also fully understand the principles behind them, providing a long-term solution to mastering the subject.

Key Concepts in Algebra 1

In this section, we will explore the fundamental principles that form the foundation of mathematical problem-solving. These essential topics are the building blocks that students need to grasp in order to solve more complex problems. Understanding these key ideas is crucial for mastering the subject and achieving success in later stages of learning.

Core Topics to Master

Here are the primary concepts students should focus on:

• Linear Equations: Understanding how to solve equations involving variables and constants.
• Operations with Polynomials: Learning how to manipulate and simplify expressions with multiple terms.
• Exponents and Powers: Grasping the rules for working with exponents in different types of problems.
• Factoring Expressions: Breaking down complex expressions into simpler components for easier solving.
• Functions and Graphing: Learning how to represent mathematical relationships visually on a coordinate plane.

Building a Strong Foundation

Mastering these topics provides the necessary tools for solving more advanced mathematical problems. Once these core concepts are understood, students will be equipped to handle more complex problems involving systems of equations, quadratic expressions, and other higher-level topics.

How to Approach Algebra 1 Problems

Solving mathematical challenges requires a clear and structured approach. By following a few key strategies, students can tackle problems with confidence and efficiency. This section outlines practical steps to help learners break down complex problems into manageable parts, making it easier to find the solution.

Step-by-Step Problem Solving

To solve any problem effectively, start by identifying the type of problem you’re facing. Once you’ve recognized the equation or expression, follow these steps:

1. Read the problem carefully: Understand what is being asked before attempting a solution.
2. Isolate variables: Focus on simplifying the equation by isolating the unknowns on one side.
3. Apply mathematical rules: Use the appropriate operations to simplify both sides of the equation.
4. Check your solution: After solving, substitute the value of the variable back into the original problem to verify the result.

Developing a Logical Mindset

Building a logical approach is key to mastering problem-solving. Each step should flow naturally from the previous one, making the process feel intuitive. With enough practice, students can develop the ability to recognize patterns and apply strategies with greater ease and accuracy.

Step-by-Step Guide to Solutions

Breaking down complex problems into smaller, manageable steps is essential for effective problem-solving. This guide provides a structured approach to help students navigate through various mathematical challenges, ensuring that each step is clear and easy to follow. By following this method, learners can confidently reach accurate solutions, even when faced with difficult tasks.

Follow These Steps for Effective Solutions

Here’s how to approach problems systematically:

1. Identify the type of problem: Understand what is being asked before diving into calculations.
2. Rewrite the problem clearly: Reorganize the given information so it’s easier to work with.
3. Simplify the equation: Combine like terms, remove parentheses, and make the problem easier to manage.
4. Apply the correct operations: Follow the rules for operations and use the right methods for solving.
5. Double-check your work: Ensure that your solution makes sense by substituting the result back into the original equation.

Practical Tips for Success

• Start with simple examples to build confidence before moving on to more complex problems.
• Always write out each step–this helps prevent errors and reinforces understanding.
• Don’t rush! Take your time to understand each part of the process thoroughly.

Common Mistakes in Algebra 1

When solving mathematical problems, even experienced learners can make errors that hinder their progress. Recognizing and avoiding common mistakes is crucial for mastering the subject and achieving consistent success. This section highlights typical errors students encounter and offers guidance on how to avoid them.

Typical Errors and How to Avoid Them

Mistake	Explanation	How to Avoid
Misapplying the distributive property	Forgetting to distribute terms correctly when simplifying expressions.	Always double-check that each term in parentheses is multiplied by the outside term.
Incorrectly solving for variables	Changing the signs or operations incorrectly when isolating variables.	Use consistent methods, and ensure each step maintains balance on both sides of the equation.
Forgetting to simplify	Leaving an expression in a more complex form than necessary.	Always simplify each expression fully before moving on to the next step.
Sign errors	Making mistakes with positive and negative signs during calculations.	Carefully track signs throughout the problem, especially when adding or subtracting.

Best Practices for Avoiding Mistakes

One effective way to minimize errors is to regularly review each step of the process before moving forward. Breaking down problems into smaller parts and verifying your work ensures accuracy. With enough practice, students will begin to identify and correct these mistakes more easily, ultimately improving their problem-solving skills.

Solving Linear Equations Efficiently

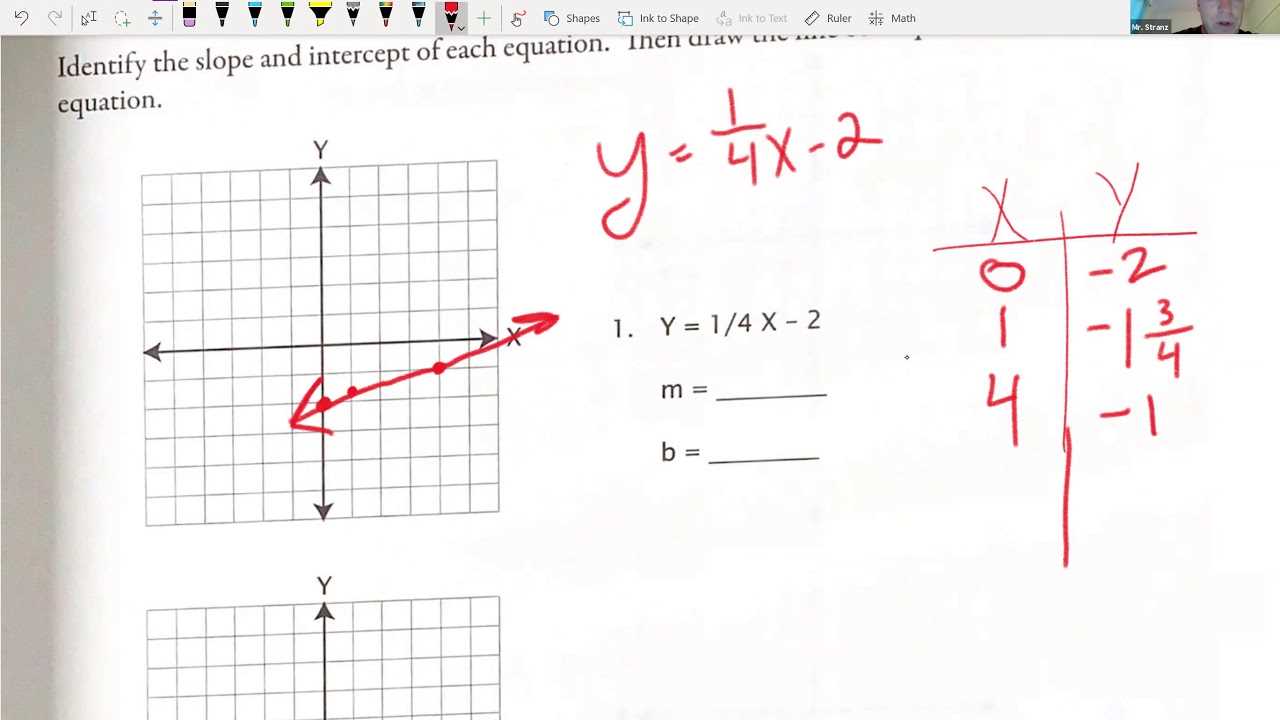
Solving equations involving variables requires a strategic approach to make the process faster and more accurate. By using efficient techniques and focusing on the most important steps, you can easily solve problems that may seem complex at first. This section outlines methods to simplify the process, ensuring that each step leads you closer to the solution without unnecessary complications.

Key Steps to Solve Linear Equations

Follow these basic steps to solve linear equations effectively:

1. Isolate the variable: Move all terms involving the unknown to one side of the equation and constants to the other.
2. Simplify both sides: Combine like terms and perform any necessary operations to make the equation easier to solve.
3. Perform inverse operations: Use addition, subtraction, multiplication, or division to isolate the variable completely.
4. Check your solution: Substitute the value back into the original equation to ensure the result is correct.

Tips for Speed and Accuracy

To solve equations more efficiently, practice regularly with simpler examples to build confidence. Always double-check your work to avoid small mistakes, especially when performing multiple operations. Over time, these techniques will become second nature, allowing you to solve problems more quickly and with greater accuracy.

Factoring Polynomials Explained

Factoring is an essential skill when simplifying expressions and solving equations. It involves breaking down complex mathematical expressions into simpler components that are easier to manipulate and solve. Understanding how to factor polynomials is key to solving various types of problems, especially when dealing with quadratic expressions or higher-degree equations.

To begin, factoring polynomials requires identifying common factors within the terms of the expression. The goal is to rewrite the polynomial as a product of simpler binomials or other factors. This process helps reveal the underlying structure of the expression, making it easier to find solutions to equations or simplify further calculations.

Working with Quadratic Equations

Quadratic equations are a central concept in solving various types of problems, especially when dealing with unknowns that appear in the form of squared terms. These equations often come in the format of a second-degree polynomial and can be solved using multiple methods, depending on the specific problem at hand. Understanding how to manipulate and solve these equations is vital for progressing in more advanced areas of mathematics.

Methods for Solving Quadratic Equations

There are several methods available for solving quadratic equations, each suitable for different types of problems:

Method	Description	When to Use
Factoring	Express the quadratic equation as a product of two binomials.	Use when the equation can be easily factored into simple terms.
Completing the Square	Rearrange the equation to form a perfect square trinomial.	Use when factoring is difficult or impossible.
Quadratic Formula	Apply the formula to find the roots of any quadratic equation.	Use when other methods are too complex or time-consuming.

Choosing the Right Approach

While all these methods can be used to solve quadratic equations, the most effective method often depends on the specific form of the equation. In some cases, factoring is the quickest option, but in others, applying the quadratic formula is more efficient. Mastery of these techniques allows students to select the most appropriate solution method, ensuring they can tackle problems more efficiently.

Tips for Solving Word Problems

Word problems often require translating real-world situations into mathematical expressions, which can seem challenging at first. The key to solving them efficiently is breaking down the problem step by step, identifying the essential information, and setting up an equation that represents the situation. This approach helps turn complex scenarios into manageable tasks.

Step-by-Step Strategy

Follow these steps to solve word problems effectively:

1. Read carefully: Understand the problem completely before attempting to solve it. Highlight or underline key details.
2. Identify variables: Define what each variable represents in the context of the problem.
3. Translate into math: Convert the problem into an equation or expression that can be solved.
4. Set up the equation: Use the information provided to form a mathematical model for the situation.
5. Solve and interpret: Solve the equation, then check if the answer makes sense in the context of the problem.

Common Mistakes to Avoid

While working through word problems, be mindful of these common pitfalls:

• Overlooking important details: Sometimes, the key information is easy to miss. Make sure to re-read the problem carefully.
• Incorrect interpretation of units: Always check the units being used (such as minutes, dollars, or meters) to avoid confusion.
• Rushing to the solution: Take your time to set up the equation properly. Rushing through the steps can lead to errors.

By practicing these strategies and avoiding common mistakes, solving word problems becomes a more straightforward process. Over time, you’ll develop a more intuitive sense for translating real-world scenarios into mathematical solutions.

Understanding Exponents and Powers

Exponents and powers are fundamental concepts that allow us to express repeated multiplication in a compact form. Instead of writing out long products, these operations use a base number and an exponent to represent how many times the base is multiplied by itself. Mastering this concept is essential for simplifying expressions and solving more complex problems involving large numbers.

What Are Exponents?

An exponent indicates how many times the base number is used as a factor in multiplication. For example, in the expression 2³, the base is 2, and the exponent is 3, meaning 2 is multiplied by itself three times (2 × 2 × 2).

Key Exponent Rules

Here are some essential rules for working with exponents:

Rule	Example	Explanation
Multiplying with the same base	am × an = am+n	When multiplying powers with the same base, add the exponents.
Dividing with the same base	am ÷ an = Graphing Equations on the Coordinate Plane Graphing equations involves plotting points on a two-dimensional grid to visually represent relationships between variables. By plotting these points and connecting them, we can create a graphical representation that allows for better understanding and analysis of the equation. The coordinate plane, with its horizontal and vertical axes, provides a clear framework for this process. Steps to Graph an Equation Follow these steps to successfully graph an equation on the coordinate plane: Identify the equation: Begin by understanding the form of the equation. Is it linear, quadratic, or another type? Knowing this helps you anticipate the shape of the graph. Find the intercepts: Determine where the graph crosses the axes. These points are critical in sketching the graph. Plot key points: Use the equation to calculate several points (x, y) and plot them on the grid. Draw the graph: Once enough points are plotted, connect them to form the graph of the equation. Make sure the graph aligns with the general shape predicted by the equation. Types of Equations and Their Graphs Different types of equations produce different types of graphs. Some common examples include: Linear Equations: These produce straight lines, and their graphs are always straight with a constant slope. Quadratic Equations: These form parabolas, which are U-shaped curves that open either upwards or downwards. Cubic Equations: The graph of a cubic equation is a curve with multiple bends. By following the steps outlined above, you can graph various equations on the coordinate plane, providing a visual representation that simplifies complex relationships between variables. Why Practice Is Essential in Algebra Repetition and consistent practice are key elements to mastering any subject, and this is especially true when it comes to mathematical problem-solving. The more you work through different types of problems, the better you understand the underlying concepts and techniques. This process helps to reinforce knowledge, build confidence, and develop problem-solving skills that are necessary for tackling increasingly complex challenges. Practicing regularly allows you to identify patterns, spot common mistakes, and gain a deeper understanding of the logic behind each step. With each new problem solved, your ability to approach new situations with clarity and precision improves. Moreover, practice leads to a natural familiarity with the various methods, making it easier to recognize the best approach to any given problem. Developing Confidence: The more you practice, the more confident you become in your ability to solve problems. Confidence is critical for tackling new and unfamiliar concepts without hesitation. Mastering Concepts: Repetition ensures that key concepts are ingrained in memory, enabling you to recall and apply them swiftly during problem-solving exercises. Problem-Solving Efficiency: Regular practice helps you to streamline your thinking, making it possible to find solutions faster and more accurately. Ultimately, the time invested in practicing regularly will pay off by improving your overall understanding and mastery of the subject, setting a strong foundation for more advanced topics in the future. How to Use the Workbook Effectively Workbooks are an essential tool for reinforcing concepts and practicing problem-solving skills. They are designed to provide step-by-step exercises that help students master core concepts. By using the workbook properly, learners can build confidence and deepen their understanding, preparing them for more advanced material. Getting Started with the Workbook Begin by reviewing the instructions provided in the workbook. Each section typically starts with a brief explanation of the concept, followed by examples that demonstrate how to solve problems. After reviewing the instructions, move on to the practice problems. Here’s how to approach them: Read Carefully: Always read each question thoroughly to understand what is being asked. Pay attention to any key information provided within the problem. Work Step by Step: Break down the problem into smaller, manageable parts. Approach each step systematically and make sure you understand why you are performing each action. Check Your Work: After solving a problem, go back and double-check your calculations. This helps to catch any errors and solidify your understanding. Maximizing Workbook Benefits To make the most of the workbook, practice regularly and don’t rush through the exercises. It’s essential to give yourself time to fully grasp each concept before moving on to the next. If you find certain problems difficult, review the instructions or seek additional resources to clarify your understanding. By using the workbook consistently and thoughtfully, you will gain a deeper understanding of the material and improve your ability to solve problems effectively. Online Resources for Help with Mathematical Concepts In today’s digital age, there are countless online resources designed to assist learners in understanding complex mathematical concepts. These tools provide a variety of instructional methods, from video tutorials to interactive exercises, ensuring that students have access to the support they need at any time. Whether you’re struggling with a particular topic or looking to sharpen your skills, the internet offers valuable opportunities for improvement. Recommended Online Platforms Here are some popular online platforms that can help you tackle difficult problems and enhance your understanding: Khan Academy: This free platform provides a comprehensive collection of instructional videos, practice exercises, and quizzes. It covers a wide range of topics and is great for building foundational skills. Wolfram Alpha: Known for its powerful computational abilities, this resource allows you to input equations and receive step-by-step solutions, making it an excellent tool for understanding the problem-solving process. Desmos: Desmos offers an interactive graphing calculator that helps visualize mathematical problems and understand concepts such as plotting functions and analyzing data. IXL: IXL provides personalized practice problems based on your skill level, allowing you to work on areas that need improvement. It also tracks your progress over time. Using Online Resources Effectively While online tools can be incredibly helpful, it’s important to use them wisely. Here are some tips to get the most out of these resources: Set Specific Goals: Before starting, decide which concepts you want to focus on. This will help you stay organized and use your time effectively. Practice Consistently: Regular practice is key to mastering any topic. Dedicate a set amount of time each week to work through problems and review explanations. Ask for Help: If you’re struggling to understand a concept, don’t hesitate to reach out to teachers or use discussion forums on platforms like Stack Exchange for additional guidance. By incorporating these online resources into your study routine, you can gain a deeper understanding of the material and improve your problem-solving abilities at your own pace. Preparing for Tests in Mathematical Concepts When preparing for assessments in any mathematical field, a strategic approach can make a significant difference in performance. A well-organized study plan, practice with sample problems, and a solid understanding of key concepts are crucial for success. In this section, we will explore effective strategies to help you prepare for tests and improve your confidence when facing mathematical challenges. Creating a Study Plan One of the first steps in test preparation is developing a study plan. This helps organize your time and ensures you cover all necessary material. Here’s how you can create an effective study plan: Break Down Topics: Divide the material into smaller, manageable sections. This allows you to focus on one concept at a time, making studying less overwhelming. Set Realistic Goals: Establish clear, achievable goals for each study session, such as mastering a particular technique or solving a set number of problems. Prioritize Weak Areas: Identify the areas where you struggle most and allocate extra time to review and practice those topics. Consistency: Set aside regular time each day for focused study. Consistency is key to reinforcing what you’ve learned and maintaining momentum. Effective Practice Techniques Practice is one of the most important aspects of test preparation. The more problems you solve, the more comfortable you’ll become with various techniques. Here are some tips for effective practice: Use Practice Tests: Take practice exams under timed conditions to simulate the real test environment. This helps build familiarity with the test format and improves time management skills. Review Mistakes: After completing practice problems, thoroughly review any mistakes. Understanding where you went wrong is essential for avoiding similar errors on the actual test. Seek Feedback: If you’re unsure about a solution or method, ask for feedback from a teacher or tutor to clarify your understanding. Work in Intervals: Study in short, focused intervals with breaks in between to maintain energy and concentration during longer study sessions. By incorporating these techniques into your preparation routine, you’ll be better equipped to tackle the material with confidence and perform well on your upcoming test.