
Building confidence in numerical reasoning is essential for tackling complex concepts in any subject involving calculations. Understanding key principles lays a strong groundwork for advanced exploration.
In this guide, we provide a clear path to breaking down intricate problems into manageable steps. With thoughtful explanations and practical tips, learners can enhance their comprehension and develop effective strategies.
Whether navigating relationships between variables or decoding abstract scenarios, our approach focuses on simplifying concepts to make them accessible and intuitive. This resource is designed to empower students with tools for academic success and practical application.
Comprehensive Overview of Springboard Math Course
Understanding core numerical principles is key to building a strong foundation for more advanced studies. A well-structured program offers students the chance to explore concepts through guided practice and logical progression, ensuring they develop essential problem-solving skills step by step.
Building Strong Analytical Skills
One of the primary goals is to strengthen analytical thinking by teaching learners how to identify patterns, work with expressions, and approach challenges methodically. These skills not only boost confidence but also prepare students for more complex problem-solving scenarios.
Progressing Through Logical Steps
The material is designed to progress gradually, introducing new topics in a structured manner. This ensures learners can connect previously mastered ideas with upcoming concepts, creating a seamless learning experience that reinforces comprehension and retention.
Key Concepts in Pre Algebra Explained
Understanding foundational ideas in numerical reasoning is vital for navigating both academic and practical challenges. These principles serve as the cornerstone for more complex problem-solving and analytical thinking.
Essential Elements of Number Operations
- Combining and manipulating values effectively to simplify tasks.
- Applying rules such as commutativity and associativity to streamline processes.
- Utilizing inverse relationships to solve equations and validate results.
Interpreting and Simplifying Expressions
- Representing real-life situations through symbolic notation for easier evaluation.
- Breaking down expressions into components to identify patterns and relationships.
- Reorganizing terms to uncover solutions and understand equivalencies.
By mastering these concepts, students enhance their logical reasoning and ability to approach problems methodically, paving the way for success in more advanced studies.
How to Solve Complex Equations Easily
Tackling advanced numerical problems may seem challenging at first, but breaking them into smaller, manageable steps makes the process more approachable. By applying logical strategies, even the most intricate scenarios can be resolved efficiently.
Identifying the key components of a problem is the first step. This includes recognizing known and unknown values, as well as understanding the relationships between them. Once the structure is clear, solving becomes a matter of systematic application.
Rearranging terms to isolate the unknown helps simplify the process. Combining like terms, applying inverse operations, and checking each step for consistency ensures accuracy. This approach not only aids in finding solutions but also strengthens overall problem-solving skills.
By focusing on these methods, learners can build confidence and develop a reliable framework for solving even the most complex equations effectively.
Strategies for Understanding Math Problems
Approaching complex numerical challenges with the right mindset and strategies is key to achieving success. Breaking down a problem into simpler parts and focusing on essential details allows for clearer understanding and more effective solutions.
The first step in tackling any problem is to carefully read the question and identify what is being asked. Look for important clues, such as given values, unknowns, and relationships. This helps in forming a clear picture of what needs to be solved.
Next, visualizing the problem can often make it easier to understand. Drawing diagrams or creating charts may reveal patterns or structures that were not immediately obvious. This method also makes it easier to track your work and confirm each step.
Additionally, breaking the problem into smaller, manageable pieces allows for a more organized approach. Solve one part at a time, checking your work as you go, to ensure accuracy before moving to the next step.
With these strategies in place, learners can better navigate the challenges presented by complex numerical problems and build confidence in their problem-solving abilities.
Tips for Success in Pre Algebra Studies
Achieving success in early numerical studies requires a combination of consistent practice, a strong understanding of core principles, and effective strategies for problem-solving. By applying the right techniques, learners can overcome challenges and build a solid foundation for more advanced topics.
Effective Study Habits
- Practice regularly to reinforce new concepts and techniques.
- Review mistakes carefully to understand where errors occurred and how to avoid them.
- Break study sessions into smaller, focused blocks to maintain concentration and avoid burnout.
Mastering Key Skills
- Focus on understanding the logic behind each step rather than memorizing solutions.
- Learn to identify patterns in problems to simplify tasks and speed up solutions.
- Use visual aids, such as diagrams or graphs, to enhance understanding and organize thoughts.
By following these tips, students can increase their proficiency and approach challenges with confidence, making progress towards mastering essential concepts.
Common Challenges and Their Solutions
As students progress through their studies, they often encounter various obstacles that can hinder their understanding. Identifying these common issues and implementing targeted strategies is essential for overcoming difficulties and improving performance. Below are some frequent challenges along with their solutions to help students stay on track.
Key Obstacles and How to Address Them

| Challenge | Solution |
|---|---|
| Difficulty understanding core concepts | Review foundational topics and seek additional examples to reinforce understanding. |
| Struggling with word problems | Break the problem into smaller parts, identify key information, and translate the words into equations. |
| Getting stuck with multi-step problems | Focus on solving each step individually, and check for errors after each stage before proceeding. |
| Lack of confidence in solving problems | Practice regularly, start with easier problems, and gradually increase difficulty to build confidence. |
By addressing these common obstacles early on, students can enhance their problem-solving skills and continue to progress in their studies with confidence.
Effective Methods for Learning Algebra Basics
Mastering the fundamentals of mathematical operations is crucial for progressing in more advanced topics. To develop a solid understanding, it’s important to apply a variety of techniques that break down complex concepts into manageable steps. These methods focus on reinforcing key skills and promoting retention through consistent practice and active problem-solving.
One effective approach is starting with the core principles such as variables, constants, and basic operations. By learning how to manipulate these components, students can build a strong foundation. Additionally, visual aids like charts and diagrams can help clarify abstract ideas and make the material more tangible.
Another helpful method is practicing with real-world examples that apply mathematical concepts to everyday situations. This approach makes the material more relevant and easier to grasp. As students progress, gradually increasing the difficulty level of exercises ensures they are continuously challenged while reinforcing what they’ve learned.
Practical Applications of Algebra in Real Life
Mathematical concepts extend far beyond the classroom and play a vital role in everyday life. By understanding how to solve equations and manipulate variables, individuals can tackle real-world problems more effectively. These skills are essential for making informed decisions, managing finances, and solving various practical challenges.
Everyday Uses of Mathematical Principles
Here are a few ways in which basic mathematical operations are used in daily life:
- Budgeting and Financial Planning: Managing personal finances involves calculating expenses, savings, and income, often requiring the use of equations to balance budgets and predict future financial trends.
- Home Improvement Projects: Whether it’s calculating the amount of paint needed for a wall or determining the dimensions for a new piece of furniture, mathematical formulas help in making precise measurements and estimates.
- Shopping Discounts: Understanding percentages and price calculations helps individuals take advantage of sales, discounts, and compare prices effectively.
- Cooking and Recipe Adjustments: Scaling ingredients in recipes, adjusting portions, and understanding ratios are common tasks that require basic math skills.
Career Fields Benefiting from Math Knowledge
Many professions require knowledge of basic mathematical principles, including:
- Engineering: Engineers rely on mathematical equations to design structures, optimize systems, and troubleshoot technical issues.
- Architecture: Architects use calculations to ensure building designs are structurally sound and meet required specifications.
- Science and Research: Data analysis, experiments, and scientific modeling depend on mathematical methods to derive accurate conclusions and predictions.
- Technology: Programming, software development, and data analytics involve solving complex problems using logical equations and algorithms.
Understanding how to apply these concepts can empower individuals to navigate challenges and make better decisions in their personal and professional lives.
Understanding Variables and Expressions

In solving mathematical problems, the ability to understand and manipulate variables and expressions is fundamental. These elements are the building blocks for more complex operations and can help solve a wide range of real-world issues. A variable acts as a placeholder for numbers, while expressions combine these variables with numbers and operations to represent a specific quantity or relationship.
What is a Variable?

A variable is a symbol, often a letter like x, y, or z, that represents an unknown value. The purpose of using variables is to solve problems when some information is missing or when dealing with general relationships. In simpler terms, a variable stands in for a value that can change or be determined depending on the context.
What is an Expression?
An expression is a combination of numbers, variables, and operations (such as addition, subtraction, multiplication, and division). Unlike an equation, an expression does not have an equals sign and cannot be solved, but it can be simplified or evaluated by substituting specific values for the variables.
| Expression | Explanation |
|---|---|
| 2x + 5 | This expression means “two times a variable, plus five.” The variable x can be replaced by a number to find its value. |
| 3a – 4b | In this expression, a and b are variables, and the equation indicates that three times a, minus four times b, should be calculated. |
| 5(x + 2) | This is a more complex expression, where the value of x is increased by 2, then multiplied by 5. |
By understanding how variables and expressions work, individuals can apply these concepts in various situations, ranging from simple calculations to solving complex problems in engineering, science, and finance.
Step-by-Step Solutions for Math Exercises
Breaking down complex problems into smaller, manageable steps is essential for understanding and solving mathematical challenges effectively. By following a clear process, each stage of a problem can be tackled individually, which helps avoid confusion and ensures accuracy in the final result.
Here is a guide to approach solving problems step by step:
- Identify the Problem: Read the exercise carefully to understand what is being asked. Identify key elements such as variables, numbers, and operations.
- Plan the Approach: Decide which method or formula is best suited for solving the problem. This could involve simplifying expressions, balancing equations, or using arithmetic operations.
- Execute the Steps: Apply the necessary operations to the problem. Work through each part methodically and check your progress along the way.
- Review the Solution: Once the answer is obtained, revisit the problem to verify if the solution makes sense. Double-check each step to ensure there were no errors.
Following this process can make solving even the most complicated problems more manageable. Practice will also help in developing a deeper understanding and ability to approach similar challenges with confidence.
Resources for Enhancing Math Knowledge

To build a strong foundation in solving numerical problems and understanding key concepts, it is essential to utilize a variety of learning tools and materials. These resources provide valuable support and offer different approaches for mastering essential skills, from interactive lessons to in-depth textbooks and online platforms.
- Online Tutorials: Websites and educational platforms offer video tutorials that explain concepts in an easy-to-understand manner. These can be helpful for visual learners and those looking for step-by-step guidance.
- Practice Problems: Regular practice is key to reinforcing skills. Many websites provide a wide range of exercises with varying levels of difficulty, allowing learners to test their knowledge and improve their problem-solving abilities.
- Interactive Apps: Mobile applications and software tools can enhance learning through engaging, hands-on experiences. These apps often include games, quizzes, and instant feedback to make learning more dynamic.
- Study Groups: Collaborating with peers in study groups allows for the exchange of ideas and solutions. Discussing problems with others can help clarify doubts and reinforce understanding.
- Textbooks and Workbooks: Traditional textbooks remain an important resource. They offer structured lessons, examples, and exercises designed to guide learners through fundamental topics.
By combining these resources, learners can enhance their understanding, practice effectively, and strengthen their overall grasp of mathematical concepts.
Importance of Practice in Pre Algebra
Mastering basic problem-solving skills requires consistent and focused effort. Repeatedly working through exercises helps to reinforce concepts, deepen understanding, and improve accuracy in calculations. By practicing regularly, learners gain the confidence needed to tackle increasingly complex tasks and develop a solid foundation for future learning.
Engaging with a variety of problems allows individuals to strengthen their critical thinking abilities and sharpen their skills in applying mathematical rules. Without sufficient practice, even well-understood concepts can become difficult to recall when needed, leading to gaps in knowledge. Hence, regular practice is a key element in building proficiency and success.
Exploring Patterns and Relationships in Math
Recognizing patterns and understanding relationships are fundamental skills in solving mathematical problems. Patterns provide a framework for predicting outcomes and recognizing structures, making it easier to solve complex problems. By identifying recurring sequences or relationships between numbers and variables, individuals can simplify calculations and find efficient solutions.
Exploration of these patterns allows learners to build a deeper understanding of underlying principles. From basic sequences to more advanced functions, the ability to spot trends is crucial for connecting various concepts. Whether it’s through visualizing geometric shapes, analyzing number patterns, or understanding functional relationships, discovering these connections enhances problem-solving abilities and fosters a more intuitive approach to learning.
Understanding Linear Equations Made Simple
Linear equations are an essential concept that can often seem intimidating, but with a clear understanding, they become straightforward to solve. These equations represent relationships between variables where the highest power of the variable is one, making them easy to work with. Once you grasp the fundamental structure, solving these equations becomes a step-by-step process that anyone can master.
Key Elements of Linear Equations
Before solving linear equations, it is important to understand the main components involved:
- Variables: Symbols that represent unknown values, often denoted as “x” or “y”.
- Coefficients: Numbers that multiply the variables, determining their scale.
- Constants: Fixed values in the equation that do not change.
Step-by-Step Approach to Solving Linear Equations
Follow these basic steps to solve most linear equations:
- Isolate the variable: Begin by moving all terms containing the variable to one side of the equation.
- Simplify the equation: Combine like terms and perform operations such as addition or subtraction to simplify the equation.
- Solve for the variable: Divide or multiply both sides of the equation by the coefficient of the variable to find its value.
Advanced Problem-Solving Techniques for Students
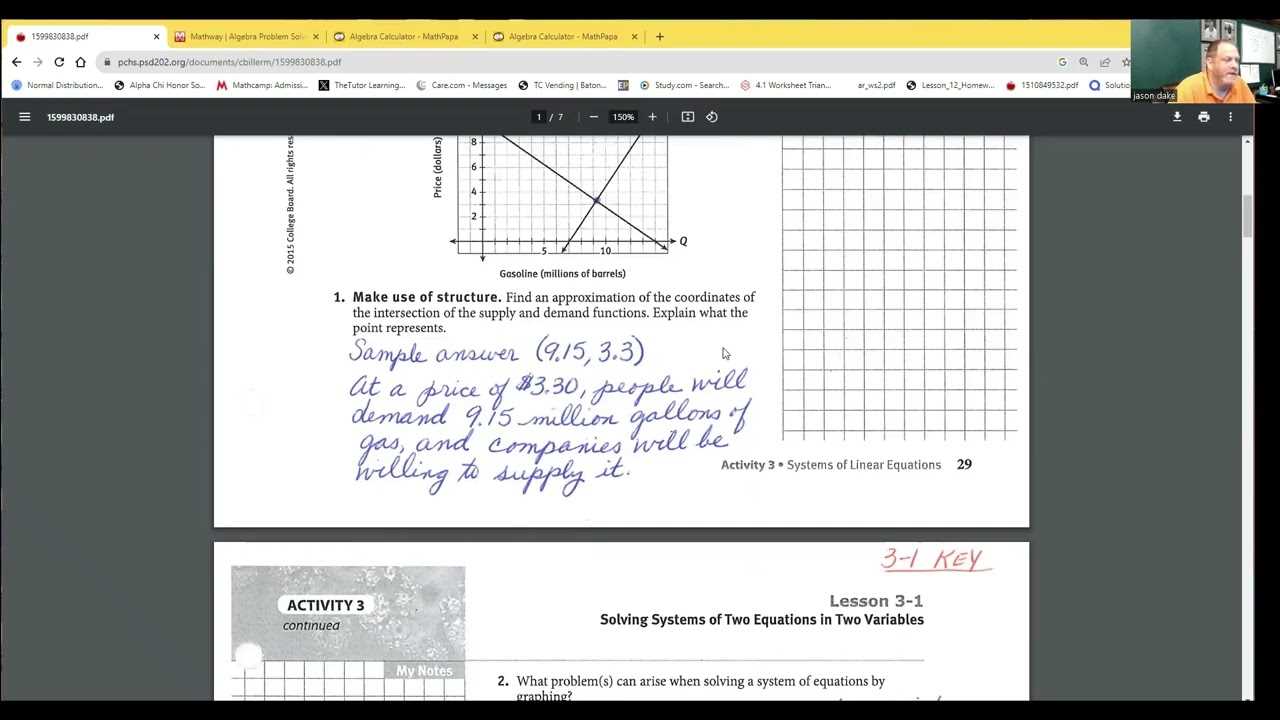
When tackling complex mathematical challenges, students often need more than just basic skills. Advanced problem-solving techniques enable individuals to approach problems from multiple angles and find efficient solutions. These strategies can be applied to a variety of problems, improving both critical thinking and overall performance. The following methods help students navigate through difficult questions with ease and confidence.
Strategic Use of Patterns and Sequences
Recognizing patterns is one of the most powerful tools in solving advanced problems. Patterns can simplify complicated equations and lead to quicker solutions. Look for repeating sequences, symmetrical arrangements, or arithmetic progressions that can break down the problem into manageable parts. This method is especially useful when dealing with large datasets or complex functions.
Decomposition and Breaking Down Complex Problems

Decomposition involves breaking down a complex problem into smaller, simpler steps. By solving each smaller segment, the overall problem becomes much easier to handle. This technique is particularly helpful in multi-step problems, where each part of the problem builds upon the previous one. Tackle the problem step by step, ensuring a deep understanding of each individual element before moving on to the next.
Benefits of Using Answer Guides Effectively
Using answer guides can significantly enhance learning by providing valuable insights and step-by-step solutions to complex problems. When utilized properly, these resources help students grasp concepts more quickly, identify mistakes, and improve their problem-solving skills. However, it’s important to approach them with the right mindset to maximize their potential. Below are key benefits that highlight the importance of using such guides effectively in the learning process.
Improved Understanding of Problem-Solving Methods
Answer guides offer detailed solutions that demonstrate the methods used to arrive at a correct answer. By following these steps, students can gain a deeper understanding of the logic behind each problem. This process not only clarifies the solution but also strengthens the student’s ability to apply similar methods to new and varied problems.
Boosting Confidence and Reducing Frustration

When faced with challenging exercises, students often experience frustration. Answer guides help alleviate this by offering a clear path to follow, reducing confusion. Understanding how a solution is built step by step boosts confidence, allowing students to feel more capable in approaching future problems independently.