Eureka Math Grade 8 Module 1 Answers and Solutions

​

Eureka Math Grade 8 Module 1 Answers

In this section, we will explore key solutions for the first set of exercises designed to build a strong foundation in algebraic concepts. The focus is on guiding students through the process of solving complex problems, providing detailed steps to ensure clarity and understanding. These solutions will help reinforce the fundamental skills needed for more advanced topics.

Understanding Key Techniques

Breaking down expressions and solving linear equations are core skills that students will develop throughout this unit. By practicing these techniques, learners will gain the ability to tackle a wide range of algebraic challenges with confidence. Each step is explained thoroughly, ensuring that no detail is missed and that every problem is approached logically.

Step-by-Step Guidance for Success

Through a series of practical examples, students will gain a deeper understanding of mathematical relationships and how to manipulate them effectively. These carefully explained procedures will assist in grasping more complex topics, laying the groundwork for future learning and ensuring academic success.

Overview of Module 1 Content

This section introduces essential topics that form the basis for understanding algebraic concepts. It focuses on building a solid understanding of basic mathematical operations and their application in problem-solving. Students will develop their ability to simplify expressions, solve equations, and interpret various mathematical relationships.

Key Topics Covered

• Simplifying expressions using distributive property
• Solving linear equations with one variable
• Working with inequalities and their solutions
• Understanding and graphing coordinate plane points
• Applying strategies to solve word problems

Skills to Develop

1. Accurate interpretation of algebraic equations
2. Confidence in solving multi-step problems
3. Understanding the relationship between variables
4. Effective use of mathematical reasoning and logic

Throughout this section, students will also engage with real-world problems to connect theoretical concepts with practical applications. This approach helps to solidify their understanding and prepares them for more complex topics in future lessons.

Key Concepts in Grade 8 Math

This section focuses on the fundamental principles that students need to master in order to succeed in algebraic reasoning. Key ideas include understanding expressions, equations, and their relationships, which form the building blocks for more complex mathematical topics. By mastering these concepts, students will be prepared for tackling a wide range of problems and applying their skills in real-world scenarios.

Essential Principles

Concept	Description
Expressions	Understanding and simplifying algebraic expressions with variables and constants.
Equations	Solving linear equations and finding the value of unknowns.
Inequalities	Interpreting and solving inequalities with multiple solutions.
Graphing	Plotting points and understanding the coordinate plane for visualizing relationships.
Problem-Solving	Applying logical reasoning to solve real-world word problems.

Mastering these key ideas will not only enhance problem-solving skills but also improve logical thinking, a crucial ability in both academic and practical applications. The understanding of expressions, equations, and graphs will be critical for progressing in more advanced subjects and in everyday situations involving quantitative reasoning.

How to Solve Module 1 Problems

Solving problems in this section requires a clear understanding of the underlying concepts and the steps involved in working through each problem. By breaking down each task into smaller, manageable parts, students can approach each question logically and methodically. This approach helps ensure accuracy and builds confidence in solving more complex challenges.

Step-by-Step Approach

Follow these essential steps to solve problems effectively:

1. Read the Problem Carefully: Identify the key information and what the question is asking.
2. Write Down Known Values: Highlight given numbers, variables, and any other relevant data.
3. Set Up the Equation: Translate the problem into a mathematical expression or equation.
4. Simplify the Expression: Use appropriate rules to combine like terms and simplify where possible.
5. Solve for the Unknown: Apply algebraic methods to isolate the variable and solve.
6. Check Your Solution: Plug the solution back into the original problem to ensure it is correct.

Common Strategies to Use

• Distributive Property: Use this to simplify expressions involving multiplication over addition or subtraction.
• Substitution: Substitute known values into equations to simplify and solve.
• Elimination: Use this method for solving systems of equations when both variables need to be isolated.
• Graphing: Visualize solutions by plotting on a coordinate plane for linear equations.

By practicing these techniques regularly, students will become more efficient at solving problems and develop a deeper understanding of the principles that underpin them.

Step-by-Step Solutions for Each Lesson

In this section, we will break down the steps to solve key problems from each lesson. By following a structured approach, students can learn how to tackle each question with clarity and precision. Each solution is presented in a way that builds on the previous concepts, ensuring a solid understanding of the material.

Solving Problems Efficiently

To solve problems effectively, follow this systematic process for each lesson:

1. Identify the Problem: Read the question carefully to understand what is being asked. Identify the known and unknown values.
2. Write the Equation: Translate the problem into a mathematical expression or equation that can be solved.
3. Simplify the Expression: Combine like terms or apply necessary properties to make the equation easier to solve.
4. Isolate the Variable: Use algebraic methods to solve for the unknown variable by isolating it on one side of the equation.
5. Verify the Solution: Substitute the solution back into the original problem to ensure accuracy.

Example Walkthroughs

Here are some common types of problems and the steps used to solve them:

• Linear Equations: Solve for the unknown by using inverse operations to isolate the variable.
• Word Problems: Convert the verbal description into a mathematical equation, then solve using appropriate techniques.
• Inequalities: Follow the same steps as for equations, but remember to reverse the inequality sign when multiplying or dividing by a negative number.
• Graphing: Plot points on a coordinate plane and draw lines to represent equations visually.

By following these structured steps, students will be able to approach any problem with confidence and accuracy, ensuring a deeper understanding of the material covered in each lesson.

Common Mistakes to Avoid

While working through algebraic problems, it’s easy to make simple mistakes that can lead to incorrect results. Recognizing and avoiding these common errors is essential for improving accuracy and efficiency. By understanding these pitfalls, students can develop better problem-solving habits and reduce the chances of making the same mistakes repeatedly.

Common Errors in Problem-Solving

• Misinterpreting the Question: Always ensure you fully understand what the problem is asking before attempting to solve it. Misreading can lead to unnecessary confusion and incorrect solutions.
• Neglecting to Simplify Expressions: Often, problems require simplifying expressions before solving. Skipping this step can make equations harder to solve or lead to errors later in the process.
• Incorrectly Applying Properties: When dealing with equations, it’s crucial to apply properties like the distributive property or inverse operations correctly. Misapplying these can cause significant mistakes.
• Forgetting to Check the Solution: After solving, always substitute the result back into the original problem to verify that it satisfies the equation. Many errors can be avoided with this final check.

Common Graphing Mistakes

• Plotting Points Incorrectly: Ensure that each point is plotted in the correct location based on the coordinates. A small mistake here can lead to an entirely wrong graph.
• Ignoring Scale on the Axis: Pay attention to the scale on both axes when graphing. Misjudging the scale can cause distortion in the graph, leading to inaccurate conclusions.

By being mindful of these common mistakes, students can improve their problem-solving skills and gain more confidence in tackling algebraic challenges.

Tips for Understanding Expressions

Algebraic expressions can seem complex at first, but with the right approach, they become much easier to understand. The key is breaking down each part of the expression and recognizing how different elements relate to one another. By practicing basic strategies, students can improve their ability to interpret and simplify expressions, making problem-solving faster and more accurate.

Breaking Down Expressions

To gain a clearer understanding, it’s essential to approach expressions step by step:

• Identify Terms: Each part of the expression, separated by addition or subtraction, is called a term. Recognize these to understand how they fit together.
• Understand Coefficients: The number multiplying a variable is called the coefficient. It’s crucial to know that coefficients indicate the number of times a variable is added or subtracted.
• Recognize Constants: Constants are numbers without variables. These are important for setting up the structure of an equation.
• Look for Like Terms: Like terms share the same variable raised to the same power. Combining these simplifies expressions and makes them easier to solve.

Tips for Simplification

Once the components are understood, simplifying expressions becomes much easier:

• Use the Distributive Property: Multiply numbers outside parentheses by each term inside to simplify complex expressions.
• Combine Like Terms: Add or subtract terms with the same variable and exponent to make expressions simpler.
• Apply Parentheses Carefully: Parentheses indicate operations that should be performed first, so always simplify inside them before moving to other parts of the expression.

By practicing these strategies regularly, students will become more comfortable with algebraic expressions and gain a stronger grasp of how to manipulate and simplify them effectively.

Working with Equations and Inequalities

Solving algebraic expressions often involves working with relationships between quantities. Whether dealing with equalities or inequalities, the goal is to manipulate the given terms to isolate the unknowns and find a solution. These problems can be approached similarly, though inequalities introduce additional considerations related to the range of possible solutions. Understanding the proper methods for each is key to successfully solving these types of problems.

Solving Equations

Equations are statements that express equality between two parts. Solving them involves finding the value of the unknown variable that makes both sides of the equation true. The process typically involves:

• Isolating the variable: Use inverse operations to move terms around and simplify the equation.
• Performing calculations carefully: Follow mathematical rules and check each step for accuracy.
• Substituting the solution: After solving, plug the value back into the equation to verify it satisfies both sides.

Solving Inequalities

Inequalities, on the other hand, express a relationship that is not necessarily equal but reflects a range of possible values. The steps to solving inequalities are similar to solving equations, with one key difference:

• Reversing the inequality: If multiplying or dividing by a negative number, reverse the direction of the inequality sign.
• Checking possible values: Since inequalities have multiple solutions, test various values within the solution set to ensure they satisfy the inequality.

Example Table

Expression	Steps	Solution
3x + 5 = 14	Subtract 5, then divide by 3	x = 3
4x – 7 > 9	Add 7, then divide by 4	x > 4
2x + 8 ≤ 18	Subtract 8, then divide by 2	x ≤ 5

By mastering the techniques for solving equations and inequalities, you’ll develop the confidence to tackle increasingly complex problems with ease.

Explaining Word Problems in Module 1

Word problems can seem daunting at first, but they are a practical way to apply mathematical concepts to real-world situations. These types of problems require translating a written scenario into a mathematical expression or equation. The key is to carefully read the problem, identify the important information, and determine what needs to be solved.

Understanding the Problem

Before jumping into calculations, it’s essential to break down the word problem into manageable parts. Here’s how to approach it:

• Identify the question: What exactly is the problem asking you to find or solve?
• Extract the data: Look for numbers, variables, and relationships between quantities that are mentioned in the text.
• Determine the operations: Decide which mathematical operations (addition, subtraction, multiplication, etc.) are needed to solve the problem.

Setting Up the Equation

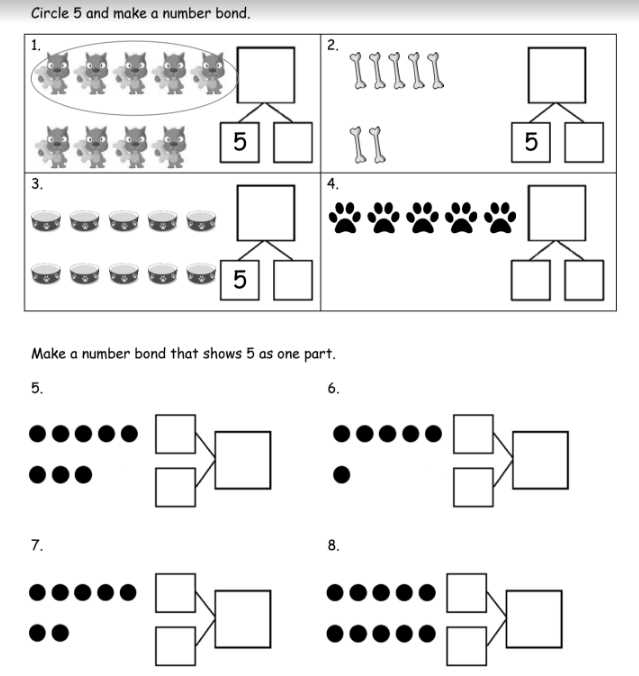
Once the problem is understood, the next step is to translate the scenario into a mathematical equation or inequality. This requires recognizing the patterns and relationships described in the problem. Here’s a simple approach to setting up the equation:

• Use variables: Assign variables to unknown quantities, such as “x” for an unknown number.
• Translate words into symbols: Convert phrases like “more than,” “less than,” or “twice” into their mathematical equivalents (e.g., “more than” becomes “+”).
• Form the equation: Use the relationships between the numbers and variables to create a solvable equation.

By practicing these steps, you can effectively solve word problems and apply your knowledge to real-world situations with confidence.

Strategies for Simplifying Expressions

Simplifying expressions is an essential skill in solving algebraic problems efficiently. The goal is to reduce complex expressions to their simplest form, making them easier to solve and understand. By following a few fundamental strategies, you can streamline the process and avoid unnecessary steps.

Combining Like Terms

One of the first steps in simplifying an expression is to combine like terms. Like terms are terms that have the same variable raised to the same power. Here’s how to handle them:

• Identify like terms: Look for terms that have the same variable and exponent, such as 3x and 5x.
• Combine the coefficients: Add or subtract the numbers in front of the variables. For example, 3x + 5x becomes 8x.
• Leave constants separate: Keep constant terms, such as 7 or -3, separate from variable terms.

Distributive Property

The distributive property is another powerful tool for simplifying expressions. This property allows you to multiply a term outside the parentheses by each term inside the parentheses. Here’s how to apply it:

• Distribute the multiplier: Multiply the outside term by each term inside the parentheses. For example, 2(x + 3) becomes 2x + 6.
• Simplify the result: After distributing, combine any like terms if necessary.

By mastering these techniques, you can simplify even the most complicated expressions and move toward finding the solution with greater ease.

Using the Distributive Property

The distributive property is a fundamental rule in algebra that allows you to multiply a term outside of parentheses by each term inside the parentheses. This technique simplifies expressions and makes calculations easier by breaking down complex operations into simpler steps. It is especially useful when dealing with multiplication of binomials or more complex expressions.

Applying the Distributive Property

To apply the distributive property, follow these steps:

• Identify the term outside the parentheses: This is the multiplier that will be distributed to each term inside the parentheses.
• Multiply each term inside: Distribute the multiplier to each term inside the parentheses. For example, 3(a + 4) becomes 3a + 12.
• Simplify: After distributing, combine any like terms if necessary.

Example of Distributive Property

Consider the expression 5(x + 2). To simplify it using the distributive property:

• Multiply 5 by x, which gives 5x.
• Multiply 5 by 2, which gives 10.
• Thus, 5(x + 2) simplifies to 5x + 10.

Using the distributive property helps to break down more complicated expressions into simpler parts, making problem-solving more manageable.

Solving Linear Equations Effectively

Solving linear equations is a crucial skill in algebra, involving finding the value of a variable that makes the equation true. The process typically involves simplifying the equation step by step, isolating the variable on one side, and applying inverse operations to solve for its value. Mastering these techniques can make solving such equations quicker and more accurate.

To solve a linear equation effectively, follow these key steps:

• Simplify both sides: Combine like terms and eliminate any parentheses if present.
• Move variables to one side: Use addition or subtraction to get all terms involving the variable on one side of the equation.
• Isolate the variable: Use multiplication or division to solve for the variable by isolating it on one side.
• Check your solution: Always substitute the value of the variable back into the original equation to ensure it satisfies the equation.

For example, consider the equation 3x + 5 = 11. To solve it:

• Subtract 5 from both sides: 3x = 6
• Divide both sides by 3: x = 2

By following these steps systematically, you can confidently solve linear equations and ensure your solutions are correct.

Graphing Solutions on a Coordinate Plane

Graphing solutions on a coordinate plane is a fundamental concept that allows you to visualize relationships between variables. By plotting points that represent solutions, you can gain a clear understanding of how values interact and how they fit within a specific equation or inequality. The coordinate plane consists of two axes: the horizontal axis (x-axis) and the vertical axis (y-axis), where each point is represented by a pair of coordinates.

To graph a solution, follow these steps:

• Identify the coordinates: The solution will typically be given as an ordered pair, such as (x, y), where x is the horizontal value and y is the vertical value.
• Locate the point: Begin at the origin (0, 0) and move along the x-axis by the value of x, then move along the y-axis by the value of y.
• Plot the point: Mark the point where the two movements intersect, which represents the solution on the graph.

For example, if the solution is (3, 2), you would start at the origin (0, 0), move 3 units to the right along the x-axis, and then move 2 units up along the y-axis. The point (3, 2) would be plotted at the intersection of these two movements.

Graphing solutions not only helps with understanding individual equations, but it also provides insight into the relationship between multiple variables and how they behave in different contexts.

How to Tackle Multi-Step Problems

Multi-step problems require a systematic approach to break down complex tasks into smaller, manageable parts. These problems often involve a series of operations, such as addition, subtraction, multiplication, or division, applied in a sequence to reach the final solution. Understanding how to approach these problems step by step can make them much easier to solve.

Here are some strategies to effectively solve multi-step problems:

Step 1: Understand the Problem

Before starting any calculations, read the problem carefully to understand what is being asked. Identify the important information and write it down. Make sure you know the final result you’re trying to achieve, whether it’s finding a value for a variable, solving an equation, or determining a quantity.

Step 2: Break Down the Steps

Once you understand the problem, identify the sequence of operations required. Break down the problem into smaller tasks and tackle them one at a time. This approach ensures you stay organized and helps prevent confusion during calculations. If necessary, work backwards from the final result to determine the intermediate steps.

• Start with simpler operations: If the problem involves multiple operations, begin with the simplest one. This can simplify the overall process and make it easier to move forward.
• Check your work after each step: After completing each calculation, double-check your work to ensure accuracy before moving on to the next step.
• Use estimation: When possible, estimate intermediate values to check if your calculations are reasonable and to catch any errors early on.

By following these steps and practicing regularly, you can build your confidence and ability to solve multi-step problems efficiently and accurately.

Understanding Mathematical Relationships

Mathematical relationships describe how different quantities interact with each other. Understanding these connections is crucial for solving problems effectively, as it allows you to recognize patterns and apply the right operations. These relationships can be expressed through equations, graphs, and tables, and they form the foundation for more complex concepts and problem-solving strategies.

In this section, we’ll explore key relationships commonly encountered and how they can be interpreted and utilized in different contexts.

Types of Mathematical Relationships

There are several types of relationships you may encounter in algebra and beyond. Below is a summary of the most common types:

Relationship Type	Description
Direct Proportionality	When two variables increase or decrease together in a consistent ratio, they are directly proportional. This relationship is often represented by the equation y = kx.
Inverse Proportionality	When one variable increases while the other decreases, they are inversely proportional. The relationship is expressed as xy = k.
Linear Relationships	A relationship where the graph forms a straight line. It can be described using the equation y = mx + b.
Quadratic Relationships	These involve squared terms and are represented by equations like y = ax² + bx + c. Their graphs form parabolas.

How to Interpret Relationships

To understand mathematical relationships, it’s important to recognize how the variables behave in relation to one another. For instance, in a direct proportionality relationship, if one value doubles, the other will also double. Recognizing these patterns helps in predicting outcomes and solving equations efficiently.

By understanding and applying these types of relationships, you can build a strong foundation for solving a wide variety of problems and deepening your overall comprehension of mathematical concepts.

How to Check Your Answers

Verifying your results is an essential step in problem-solving. It ensures the accuracy of your calculations and confirms that your reasoning was correct. Checking your work not only prevents mistakes but also builds confidence in your solutions. Whether you’re solving equations, working with graphs, or applying formulas, knowing how to validate your answers is key to success.

In this section, we’ll explore effective strategies for confirming the correctness of your solutions and improving your problem-solving process.

Methods for Verifying Your Work

There are several methods you can use to check if your solution is correct. Each method provides a different approach depending on the type of problem you are tackling:

• Substitution: Substitute your solution back into the original problem to see if it satisfies the equation or condition. If the left-hand side equals the right-hand side, your answer is correct.
• Reverse Operations: In problems involving multi-step calculations, perform the inverse of each operation to verify your steps. This can help catch errors made during the calculation process.
• Estimation: Check if the magnitude of your answer makes sense by approximating the numbers or using rounding. If the solution is far from what you expected, review your work.
• Graphical Verification: For problems involving graphs or geometric interpretations, plot your solution and see if it aligns with the expected outcome. A visual check can often reveal mistakes not immediately apparent in calculations.

Additional Tips for Effective Checking

Along with these methods, here are a few additional strategies to help you check your work more effectively:

• Double-Check Units: Always ensure that your final answer has the correct units. If your problem involves measurement or rates, checking units can often reveal small mistakes.
• Break Down Complex Problems: For intricate problems, break them into smaller parts. Checking each part individually makes it easier to spot where something went wrong.
• Ask for a Second Opinion: When in doubt, seek feedback from a peer or teacher. Sometimes a fresh perspective can quickly spot errors you may have missed.

By regularly applying these techniques, you can ensure that your solutions are correct and refine your problem-solving skills over time.

Review of Key Formulas and Theorems

Understanding foundational formulas and theorems is crucial for solving various problems. These essential principles serve as tools for tackling different types of questions, from solving equations to analyzing geometric shapes. By mastering these concepts, you can simplify complex tasks and build a deeper comprehension of the subject.

In this section, we will go over some of the most important formulas and theorems that are often applied in problem-solving exercises, providing a solid base for more advanced topics.

Important Formulas to Remember

Several key formulas are commonly used across a wide range of mathematical concepts. Familiarizing yourself with these will help streamline calculations and boost your ability to work through different challenges:

• Area of a Rectangle: A = length × width – Used to find the area of a rectangle by multiplying the length by the width.
• Perimeter of a Square: P = 4 × side – The perimeter of a square is four times the length of one side.
• Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a – This formula solves for x in a quadratic equation of the form ax² + bx + c = 0.
• Pythagorean Theorem: a² + b² = c² – Used to find the length of the sides of a right triangle, where a and b are the legs and c is the hypotenuse.

Key Theorems to Know

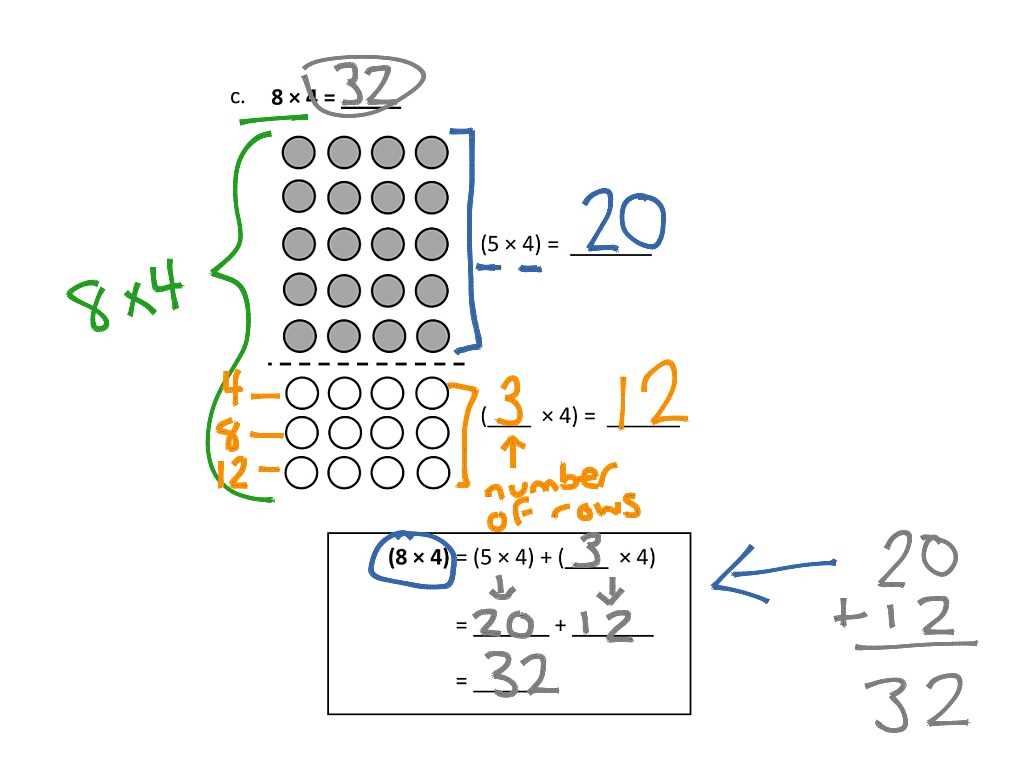
Theorems are important in building a logical framework for problem-solving, especially in areas like geometry and algebra. Here are a few theorems you should be familiar with:

• Distributive Property: a(b + c) = ab + ac – This theorem allows you to distribute multiplication over addition or subtraction.
• Commutative Property of Addition: a + b = b + a – The order of addition does not affect the sum.
• Associative Property of Multiplication: (a × b) × c = a × (b × c) – This property states that the grouping of factors in multiplication does not change the product.
• Fundamental Theorem of Algebra: Every non-constant polynomial equation has at least one complex solution.

By regularly reviewing and applying these formulas and theorems, you can develop a strong mathematical foundation that will serve you well in more advanced topics.

Preparing for the Next Module

Preparation is key to succeeding in any subject. As you move forward in your studies, it’s important to build on what you have already learned and understand how to approach the new topics ahead. Reviewing concepts, practicing skills, and strengthening your understanding of previous lessons will help ensure that you are ready to tackle upcoming challenges.

Here are some strategies to help you get ready for the next set of lessons:

• Review Key Concepts: Make sure that you have a solid grasp of the foundational principles covered so far. This will allow you to apply them more effectively to new material.
• Identify Areas of Weakness: Take time to assess which areas you struggled with. Focus your revision on those topics to strengthen your understanding and build confidence.
• Preview Upcoming Topics: Look ahead at the material that will be covered next. Try to familiarize yourself with new concepts before they are introduced in class.
• Practice Regularly: Regular practice is essential for retaining knowledge. Solve problems, work through exercises, and revisit past assignments to reinforce your learning.
• Seek Help When Needed: If you find yourself struggling with a specific topic, don’t hesitate to ask for help. Teachers, tutors, or online resources can provide additional explanations and support.

By following these steps, you can approach the next set of lessons with confidence and readiness, ensuring a smoother transition to more advanced material.