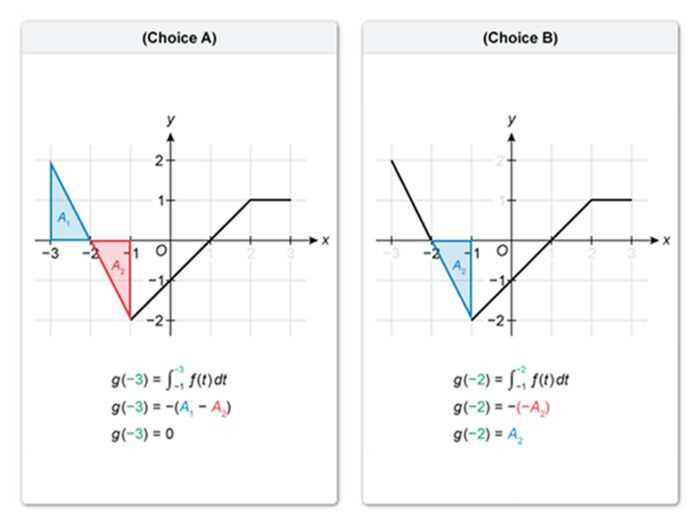
Preparing for the AP Calculus BC exam can be a daunting yet rewarding challenge. The exam evaluates a wide range of mathematical concepts and skills that are essential for students pursuing advanced studies in mathematics and science. Effective preparation is key to mastering the material and performing well on the test.
One of the most critical components of the exam is its problem-solving format, which requires a deep understanding of both theoretical and practical concepts. By practicing different types of questions and refining your problem-solving approach, you can improve your accuracy and speed. The exam includes various questions designed to test your ability to apply concepts in real-world scenarios, making it crucial to focus on both the fundamentals and more complex topics.
With the right strategies and resources, students can feel confident approaching the exam. Understanding how to approach different types of questions, managing time effectively, and reviewing key concepts thoroughly are all essential to success. This article will guide you through the most effective methods for preparing for the AP Calculus BC exam and mastering its various challenges.
AP Calculus BC Multiple Choice Answers
In the AP Calculus BC exam, solving complex mathematical problems accurately and efficiently is essential to achieving a high score. The exam is designed to assess your ability to apply theoretical knowledge to practical situations, requiring not only a deep understanding of the concepts but also quick problem-solving skills. By preparing effectively, students can confidently approach the various types of questions presented.
Each question on the exam offers several options, but only one correct solution. To excel, it is crucial to recognize patterns and familiarize yourself with common techniques used in problem-solving. Some problems may seem challenging at first glance, but with careful analysis and a strategic approach, they become manageable. Focusing on simplifying the problem and eliminating obviously incorrect options can significantly increase your chances of selecting the right answer.
Strong preparation involves mastering key topics that are frequently tested, such as limits, derivatives, integrals, and series. Understanding these fundamental areas will help you navigate more complex problems and improve your ability to identify the correct responses. Additionally, practicing with past exams and sample questions will allow you to refine your approach and gain familiarity with the structure and difficulty of the test.
By approaching the questions with a clear strategy and using proven problem-solving methods, you can enhance your performance. Time management is also a key factor, as balancing speed with accuracy ensures that you can complete all sections without feeling rushed. Through consistent practice and a methodical review of the material, students can maximize their potential and improve their chances of success on the AP exam.
Understanding the AP Calculus BC Exam
The AP Calculus BC exam is designed to evaluate students’ understanding of advanced mathematical concepts and their ability to apply these concepts in various scenarios. It is an opportunity for students to demonstrate their skills in critical thinking and problem-solving, which are essential for success in higher education and in fields that require mathematical proficiency.
Key Components of the Exam

The exam consists of two main sections: a multiple-choice portion and a free-response portion. Each section challenges students to think critically about complex problems, requiring a solid foundation in topics such as derivatives, integrals, and series. The multiple-choice section assesses both your theoretical knowledge and your ability to apply that knowledge to solve problems quickly and accurately. The free-response portion provides a more in-depth examination, requiring you to show your work and explain your reasoning for each solution.
Types of Questions You Will Encounter
Throughout the exam, you will face a variety of question types, each designed to test a different aspect of your mathematical understanding. Some questions may focus on fundamental concepts, while others require a deeper understanding of more complex topics. Preparing for these different question types will help you build a comprehensive understanding of the material and improve your ability to solve problems efficiently.
Key Strategies for Tackling Multiple Choice
Successfully navigating the question sets on the AP exam requires more than just a solid understanding of the material; it also involves effective test-taking strategies. Knowing how to approach each problem, managing your time wisely, and avoiding common pitfalls can make a significant difference in your performance. By employing the right techniques, you can maximize your chances of selecting the correct responses and finish the exam with confidence.
One essential strategy is to read each question carefully and focus on identifying keywords or phrases that help clarify what is being asked. Often, the phrasing of a question can offer clues about the type of operation or concept you need to apply. Pay attention to details such as units, functions, or specific conditions that are presented in the problem.
Another effective approach is to eliminate obviously incorrect options. Often, there will be one or two choices that are clearly wrong. By removing these, you increase your chances of selecting the right response from the remaining options. Even if you are unsure about the correct answer, narrowing down your choices can boost your odds significantly.
Time management is also critical. Don’t get stuck on any one question for too long. If a problem feels particularly challenging, move on and return to it later if time allows. This will ensure that you have enough time to answer all questions and can give extra attention to those that are more difficult.
Finally, practicing with past exams and sample questions can help you develop these strategies in a real test environment. The more familiar you are with the types of questions and the test format, the more confident and prepared you will be on exam day.
Commonly Tested Topics in AP Calculus BC
To perform well on the AP exam, it’s essential to focus on the topics that are most frequently tested. Understanding these key areas will allow you to direct your study efforts efficiently and ensure you’re well-prepared for the exam. Below are some of the fundamental subjects that you will encounter in the exam, which form the foundation of many of the questions presented.
- Limits and Continuity – Understanding how limits behave and the concept of continuity is crucial. Expect to solve problems involving the evaluation of limits and analyzing the continuity of functions.
- Derivatives – This topic covers the basics of derivatives, including their rules and applications. Problems may ask you to find derivatives of various functions or interpret the meaning of the derivative in real-world contexts.
- Integration – Integral calculus is a major part of the exam, covering techniques for calculating areas under curves and solving problems using the fundamental theorem of calculus.
- Series and Sequences – Sequences and infinite series are important for evaluating the behavior of functions over time. Expect questions on convergence, divergence, and the applications of various series types.
- Polar Coordinates and Parametric Equations – These advanced topics require understanding how to work with polar and parametric forms of equations, along with their integration and differentiation.
By focusing on these core topics, you can tackle a wide variety of problems and improve your performance on exam day. Make sure to review each area thoroughly and practice solving problems to build both your skills and your confidence.
How to Approach Multiple Choice Questions
Successfully navigating the various questions on the AP exam requires both knowledge and strategy. While having a strong understanding of the material is essential, how you approach each question can make a significant difference in your performance. Developing a methodical approach helps reduce errors and boosts your chances of selecting the correct response.
The first step is to read each question carefully. Pay attention to specific details, as even small changes in wording can alter the meaning of the question. After reading, identify what the question is asking and the key concepts involved. This helps you focus on the relevant information and avoid being misled by extraneous details.
Next, consider all options before selecting your answer. It may be tempting to pick the first choice that seems correct, but it’s important to evaluate all responses. Often, there will be one or two answers that can be easily eliminated due to their inconsistency with the question or known facts. Eliminating these wrong answers increases your chances of choosing the correct one from the remaining options.
Time management is also crucial. Don’t spend too much time on any one question. If you’re unsure, it’s often better to make an educated guess after eliminating the obviously incorrect options rather than getting stuck. Mark the question and move on if necessary, returning to it later if time permits.
Lastly, trust your preparation. The more practice you’ve had, the more confident you will be in your ability to approach each question with a clear strategy. Practicing under timed conditions can help you simulate the test environment, reducing anxiety and improving your decision-making process when the real exam comes.
Reviewing AP Calculus BC Practice Tests
One of the most effective ways to prepare for the AP exam is by reviewing practice tests. These mock exams simulate the format and difficulty of the actual test, helping you become familiar with the structure of the questions and the time constraints. Reviewing past tests allows you to identify areas where you may need further practice and improve your problem-solving speed.
When reviewing a practice test, it’s important to focus not only on the questions you answered incorrectly but also on how you arrived at your answers. Understanding why certain choices are wrong can provide valuable insights into common mistakes and help you avoid them on the actual exam.
| Practice Test Area | What to Focus On | Action Plan |
|---|---|---|
| Concepts and Formulas | Review key formulas and concepts tested in the exam | Make a formula sheet and practice applying these in different contexts |
| Problem Solving Approach | Examine your thought process for each problem | Identify areas where your approach can be more efficient |
| Time Management | Evaluate how long you took to answer each question | Work on pacing to ensure you have time to complete all questions |
| Common Mistakes | Focus on errors you made repeatedly | Understand why they occurred and practice related problems |
By reviewing practice tests, you not only reinforce your knowledge but also build the confidence needed to tackle similar problems on the actual exam. Regularly revisiting these tests will help you refine your skills, avoid common pitfalls, and improve your overall exam performance.
Time Management Tips for the Exam
Effective time management is a critical factor for success on the AP exam. With a limited amount of time to answer a wide variety of questions, it’s essential to approach the test strategically to ensure you can complete all sections without feeling rushed. The ability to manage your time wisely not only helps you finish the exam but also allows you to answer questions with greater accuracy.
The first step is to get familiar with the time constraints for each section of the exam. Knowing how much time you have for each part will allow you to pace yourself throughout the test. Aim to spend a set amount of time on each question and avoid getting stuck on any one problem for too long. If a question seems particularly challenging, mark it and move on, returning to it later if time allows.
Another useful tip is to break the exam into manageable chunks. For example, you could set time goals for each section and track your progress. This can help you stay focused and avoid spending too much time on any single part of the exam. If you find that you’re falling behind, adjust your pacing for the remaining questions to stay on track.
In addition, practice under timed conditions leading up to the exam. Taking practice tests and simulating exam conditions will help you develop a sense of how to distribute your time effectively and give you a feel for the test’s pacing. The more you practice, the more comfortable you’ll become managing your time during the actual exam.
Lastly, don’t forget to leave a few minutes at the end to review your work. Even if you can’t answer every question, having extra time to double-check your responses will help you catch any mistakes or overlooked details.
Breaking Down Difficult AP Problems
Some questions on the AP exam can feel overwhelming, especially if they involve complex concepts or require multiple steps to solve. The key to overcoming these challenges is learning how to break down each problem into manageable parts. By approaching difficult questions systematically, you can improve your chances of finding the correct solution, even when faced with tricky scenarios.
Step-by-Step Problem Solving
The first step in tackling a challenging question is to identify what is being asked. Carefully read the problem and underline or highlight key information that will guide your solution. Look for important terms, numbers, or constraints that might indicate what method you need to use. Once you have a clear understanding of the question, break it into smaller, more manageable pieces. This allows you to address each part individually without feeling overwhelmed by the complexity of the problem as a whole.
Eliminating Unnecessary Information

Often, difficult problems will include extra details or distractions that are not directly related to the question. These can confuse you if you don’t focus on the essentials. Once you’ve identified the relevant information, ignore the extraneous parts and direct your efforts toward solving the core problem. In many cases, simplifying the question can make it much easier to approach and solve.
Additionally, if you’re unsure about your initial approach, don’t hesitate to try a different method or formula. Practice and familiarity with various techniques can help you adapt and find a strategy that works for each specific problem.
By breaking down complex questions into smaller, digestible steps and focusing on the most important information, you can increase your problem-solving efficiency and boost your confidence during the exam.
Identifying Common Mistakes in AP Problems
One of the best ways to improve your performance on the AP exam is to understand the mistakes that are commonly made by students. These errors can stem from various factors, such as misinterpreting the question, rushing through problems, or overlooking key concepts. By recognizing these common pitfalls, you can avoid them and enhance your ability to solve problems more accurately and efficiently.
Paying close attention to the most frequent mistakes will help you spot potential issues in your own work. Some of these mistakes are easy to overlook but can lead to significant errors in the final solution. Understanding these common missteps will allow you to approach each problem more carefully and with a clearer focus.
| Common Mistake | Why It Happens | How to Avoid It |
|---|---|---|
| Misreading the question | Overlooking key words or details that change the meaning | Read the question carefully and highlight important parts |
| Forgetting to apply the correct formula | Not recalling the proper method or making assumptions | Review core formulas and their appropriate applications regularly |
| Overcomplicating the problem | Trying to use advanced techniques when a simpler solution exists | Look for simpler methods before attempting more complex solutions |
| Incorrect calculations | Simple math errors or misplacing numbers during computation | Double-check calculations and ensure precision in every step |
| Time mismanagement | Spending too much time on difficult questions | Set time limits for each question and move on if stuck |
By recognizing these common mistakes and adjusting your approach accordingly, you can reduce errors and increase your chances of success. Practicing regularly and reviewing your work are key strategies for developing the confidence and accuracy needed to perform well on the exam.
Using Graphing Calculators Effectively
Graphing calculators can be powerful tools for solving complex problems on the AP exam. When used correctly, they can help you visualize functions, check computations, and save time. However, like any tool, they require practice to use effectively. Understanding how to make the most of your graphing calculator can give you an edge during the test, allowing you to focus on solving problems rather than getting bogged down by tedious calculations.
The first step in using a graphing calculator effectively is becoming familiar with its features. Many calculators have built-in functions for plotting graphs, solving equations, and performing integrations and derivatives. Understanding these functions can save you valuable time when dealing with complex expressions. Before the exam, take time to practice using these features to become comfortable with their operation and quickly navigate through problems during the test.
In addition to understanding basic functions, it’s important to know when to use the calculator and when to rely on your own reasoning. Some questions may be simple enough that using the calculator will only slow you down, while others may require its assistance to perform calculations or graph functions that are otherwise too time-consuming to handle by hand. Practice distinguishing between the types of problems that benefit from a calculator and those that can be solved without one.
Lastly, don’t forget to check your work with the graphing calculator when possible. Sometimes, seeing a visual representation of a function or solution can help you confirm whether your approach is correct. However, it’s important not to over-rely on the calculator. Always try to understand the underlying principles and reasoning behind the solution, as the exam will also assess your conceptual understanding.
Top Resources for AP Review
Preparing for the AP exam can be a challenging task, but the right study materials can make all the difference. There are numerous resources available that can help you solidify your understanding of key concepts, improve problem-solving skills, and refine test-taking strategies. Whether you prefer textbooks, online platforms, or practice exams, the following resources will provide you with the support needed to perform at your best.
- Official AP Practice Tests: The College Board offers free practice tests that closely resemble the actual exam. These tests are invaluable for understanding the format of questions and gauging your preparedness.
- Online Tutorials and Video Lessons: Websites like Khan Academy and Coursera offer free video lessons on a wide range of topics. These can help reinforce your understanding of complex topics with step-by-step explanations.
- Study Guides: Books like “Cracking the AP Exam” by The Princeton Review and “5 Steps to a 5” provide comprehensive reviews, practice questions, and tips for tackling the exam. These guides are perfect for structured, self-paced study.
- Interactive Practice Problems: Platforms like Albert.io and AP Classroom offer interactive practice questions that adapt to your progress. These websites give immediate feedback, allowing you to focus on areas where you need improvement.
- Flashcards: Flashcards are an excellent way to test your knowledge on key terms, formulas, and concepts. Apps like Quizlet offer ready-made flashcards or the option to create your own based on what you’re studying.
Using a combination of these resources will give you a well-rounded approach to exam preparation. Practice consistently, review the solutions to your mistakes, and ensure that you’re familiar with all aspects of the exam. By using these tools, you can boost your confidence and increase your chances of achieving a high score.
Understanding Answer Choices in Detail
When faced with a set of possible solutions on the exam, it’s crucial to understand each option thoroughly before making a decision. Often, questions are designed not just to test your knowledge, but also to challenge your ability to identify subtle differences between similar-looking answers. A clear understanding of how to analyze and evaluate each option can significantly improve your chances of selecting the correct one.
Start by carefully reading each option, paying close attention to small details that could indicate whether it is correct or incorrect. Sometimes, answers are crafted to include common mistakes or distractors that many students may overlook. Recognizing these can help you eliminate incorrect answers and narrow down your choices. Additionally, if you’re unsure about a particular solution, try to check if any of the answers are clearly incorrect based on your prior knowledge of the topic.
Another strategy is to recheck the question after reviewing the options. Does the wording of the question align with any of the answer choices? Sometimes, the correct solution might be hidden behind a subtle rephrasing of the problem. Be aware of answer options that are designed to seem plausible but don’t fully satisfy the question’s requirements.
Finally, remember that time is a factor. As you practice more, you’ll get better at quickly identifying and eliminating implausible solutions. This practice will help you focus on the most likely correct answers without spending excessive time on any single option.
Improving Problem-Solving Skills for AP
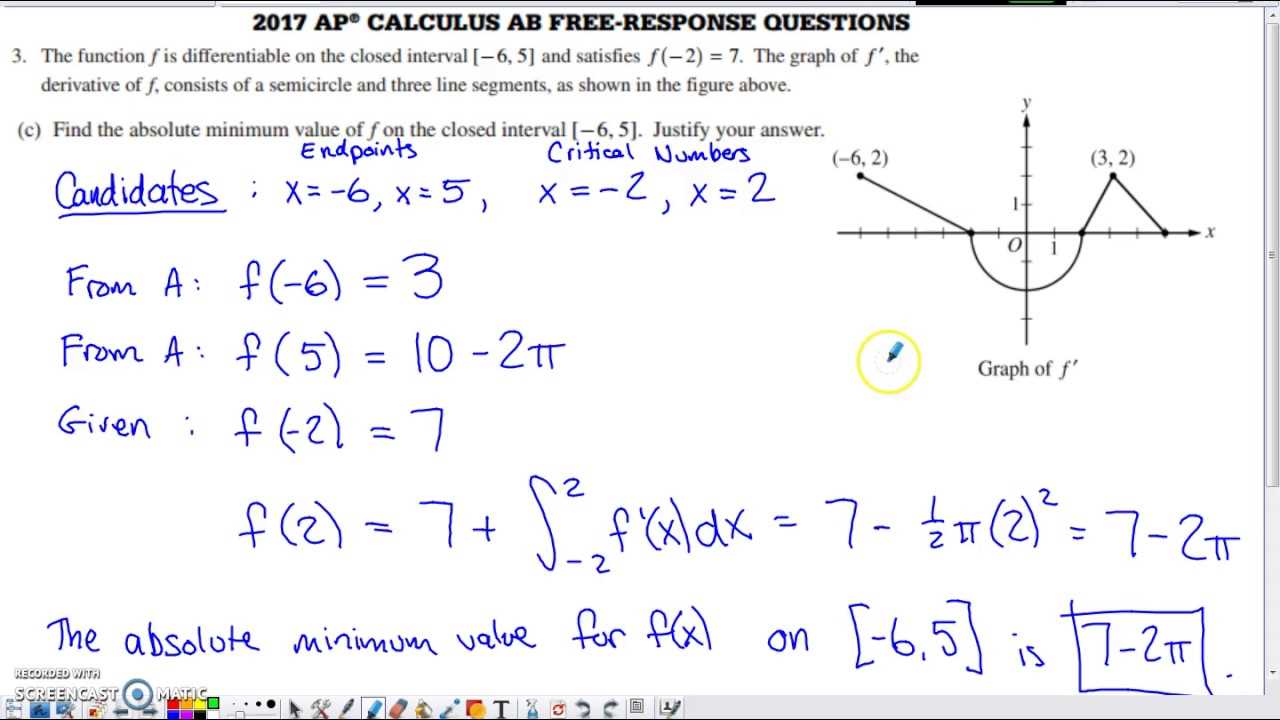
Enhancing your problem-solving abilities is essential for succeeding on the AP exam. The ability to analyze complex questions, apply appropriate methods, and arrive at a solution efficiently is a skill that can be developed with consistent practice and strategy. Whether you’re dealing with algebraic problems, integrals, or graph-related questions, honing your approach to tackling each type of problem can greatly improve your performance on the test.
One of the key ways to improve problem-solving skills is by breaking down each problem into smaller, manageable steps. Start by identifying what the question is asking and what information is provided. Then, determine which mathematical techniques or concepts are required to solve the problem. Once you’ve selected an approach, execute the steps methodically and review your work as you go along to ensure accuracy.
Another effective method is practicing a wide variety of problems. Exposure to different types of questions allows you to become familiar with various problem formats and challenges. With each problem, try to learn from your mistakes and figure out why certain approaches work better than others. This iterative process of trial, error, and reflection can help you build confidence and speed when it comes time for the actual exam.
| Problem Type | Recommended Approach |
|---|---|
| Complex Functions | Break them into simpler components and apply step-by-step techniques. |
| Graph Interpretation | Analyze key points, slopes, and behavior of the graph to make deductions. |
| Rate of Change | Use appropriate formulas and understand the context to apply the correct method. |
| Optimization | Set up equations, identify critical points, and apply reasoning to find the optimal solution. |
By incorporating these strategies into your study routine, you can improve your problem-solving skills and enhance your overall performance on the exam. Remember, consistent practice and analysis of each question will allow you to approach even the most challenging problems with greater ease and confidence.
Mastering Derivatives and Integrals
Achieving mastery in the concepts of derivatives and integrals is essential for success in advanced mathematics. These two fundamental concepts form the foundation for many problems you will encounter in the exam. A thorough understanding of how to manipulate and apply these techniques will help you solve a wide range of questions efficiently and accurately. By honing your skills in these areas, you can develop a deeper grasp of problem-solving strategies and improve your overall performance.
Understanding Derivatives
Derivatives represent the rate of change of a function. Mastery of this concept involves not just knowing the formulas, but also understanding when and how to apply them effectively. Begin by focusing on basic rules such as the power rule, product rule, and quotient rule. Practice differentiating a variety of functions, from polynomials to trigonometric expressions, to gain confidence. Additionally, learning how to interpret the meaning of a derivative in a given context–such as the slope of a tangent line or the velocity of an object–will add depth to your understanding.
Mastering Integrals

Integrals, on the other hand, are used to find the area under curves and accumulate quantities. Much like derivatives, integration requires familiarity with various techniques, such as substitution and integration by parts. Focus on understanding the fundamental theorem of calculus and how it links derivatives and integrals. Regular practice with different types of integrals, including definite and indefinite integrals, will help you become adept at solving complex problems. Additionally, learning to interpret integrals in real-world scenarios, such as finding areas or solving motion problems, will further solidify your understanding.
Key Tips for Mastery:
- Practice solving problems step-by-step to ensure a solid understanding of each technique.
- Familiarize yourself with common patterns, such as the behavior of exponential and logarithmic functions, which will help you recognize when to apply specific methods.
- Work with both symbolic and numerical problems to build fluency in both theoretical and practical applications.
By continuously practicing these techniques and seeking out new problems, you’ll be able to approach complex questions with greater confidence and precision. Mastering derivatives and integrals is not only about memorizing formulas but also about understanding their practical applications and how they interact within the broader context of advanced mathematics.
Preparing for the Free Response Section
Success in the free response section of the exam requires not just knowledge of mathematical concepts, but also the ability to apply them clearly and effectively. This part of the test challenges students to demonstrate their problem-solving skills through detailed, written solutions. It is essential to practice answering open-ended problems in a structured way, showing all necessary steps and explanations. Proper preparation will ensure that you can approach these questions with confidence, even when faced with complex scenarios.
Here are key strategies to help you prepare for this section:
Understand the Question Format
Free response questions often require a combination of calculations, explanations, and interpretations. Each question may have multiple parts, so it is important to read the question carefully and break it down into manageable steps. Pay attention to the verbs in the question, such as “find,” “explain,” or “justify,” as these will guide you in determining the type of response expected.
Practice Writing Detailed Solutions
Unlike multiple-choice questions, free response items require clear, step-by-step explanations of your reasoning. Practice writing out complete solutions, including all necessary work and justifications. Avoid skipping steps, as showing your thought process is crucial for receiving full credit. Here are some tips to improve your written responses:
- Write legibly and clearly, especially when presenting mathematical symbols or expressions.
- Label each step of your work to help the grader follow your logic.
- Show both your final answer and the reasoning behind it to ensure full credit.
Time Management During the Exam
With a limited amount of time available, managing your time effectively is crucial. Allocate a set amount of time for each question, and avoid spending too much time on any one part. If you encounter a particularly challenging question, move on to the next one and return to it later with a fresh perspective. Remember, demonstrating your problem-solving process is often just as important as reaching the correct solution.
Key Areas to Focus On
Focus on the areas most commonly tested in the free response section. These often include:
- Applications of integration and differentiation
- Modeling real-world problems with mathematical concepts
- Solving problems involving sequences and series
- Understanding limits and their applications
By consistently practicing these types of problems and refining your solution-writing skills, you’ll be well-equipped to tackle the free response section on exam day. Remember, clarity, accuracy, and thorough explanations are the keys to success.
AP Calculus BC Study Schedule Tips
Effective preparation for the exam requires a well-structured study schedule. Organizing your time wisely will allow you to focus on key areas, build strong problem-solving habits, and ensure you cover all necessary topics before the test. A carefully planned approach can help reduce stress and maximize your performance. This section provides practical tips for crafting a study schedule that fits your needs and allows you to approach the exam with confidence.
Create a Realistic Study Plan
Start by assessing how much time you have before the exam and divide it into manageable study blocks. Be realistic about how much you can study each day, and balance this with other responsibilities. Make sure to schedule time for breaks to avoid burnout. A good rule of thumb is to study in short, focused sessions (45–60 minutes) followed by a 10–15 minute break.
Prioritize Key Topics
Focus on the most critical topics that are heavily tested in the exam. These might include concepts like limits, derivatives, integrals, and series. Spend extra time on areas where you feel less confident. Incorporate different types of practice problems to ensure you fully understand each topic. Be sure to revisit challenging concepts regularly to reinforce your knowledge.
- Set weekly goals: Break down each week into specific goals, such as mastering a particular concept or completing a set of practice problems.
- Use practice exams: Include full-length practice exams in your study plan. This will help you get used to the format and timing of the real test.
- Review mistakes: After each practice test or problem set, take time to carefully review any errors. Understand why you made the mistake and how to avoid it in the future.
By following a structured study plan that emphasizes consistent practice and targeted review, you’ll be better prepared for the exam. Stick to your schedule, but stay flexible enough to adjust if you find areas that need more focus.
Building Confidence for Test Day
Confidence plays a crucial role in performing well on exam day. Building self-assurance through consistent preparation and positive mindset shifts can significantly impact your performance. This section provides strategies to help you approach the exam feeling prepared, focused, and ready to tackle any challenge. Developing the right mindset, along with solid test-taking techniques, will ensure you remain calm and composed when it matters most.
Focus on Practice and Familiarity
One of the most effective ways to build confidence is through extensive practice. The more familiar you are with the types of problems you’ll encounter, the more relaxed you will feel during the test. Consistent practice allows you to identify patterns, strengthen your problem-solving abilities, and reduce anxiety.
- Simulate real exam conditions: Take full-length practice exams under timed conditions to get used to the pressure of the real test environment.
- Review key topics: Focus on areas where you feel least confident, but also make sure to review your strengths to reinforce your knowledge.
- Track progress: Regularly assess your progress to see improvements and identify any remaining weak spots that need attention.
Maintain a Positive Mindset
A positive attitude is essential for success. Focus on the progress you’ve made rather than worrying about what you don’t know. Acknowledging your hard work and growth throughout the preparation process will help you maintain a sense of accomplishment and reduce pre-test anxiety.
- Visualization: Visualize yourself successfully answering questions and completing the exam with confidence.
- Affirmations: Use positive affirmations to counter negative thoughts and build self-belief.
- Relaxation techniques: Practice deep breathing or meditation to calm your nerves before the test.
By practicing regularly and fostering a positive mindset, you will increase your self-confidence and set yourself up for a successful exam experience. Confidence is a key ingredient in approaching challenges with clarity and focus, helping you stay on track and perform to the best of your ability.