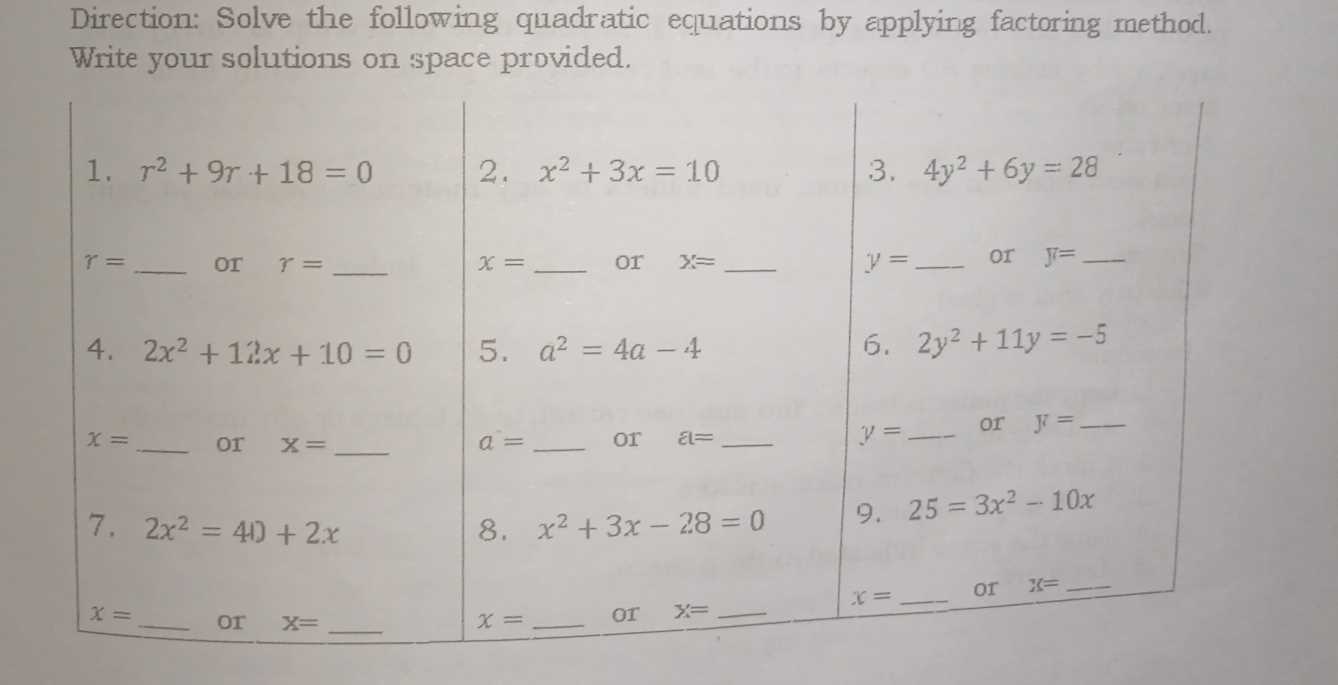
In mathematics, there are various methods for breaking down complex problems into simpler components. One such technique involves manipulating expressions to reveal their underlying structure. This approach is particularly useful when tackling expressions that involve variables and constants, allowing for a more straightforward path to find solutions.
By applying specific methods, it is possible to decompose expressions into factors that, when combined, reproduce the original problem. This process not only simplifies the task at hand but also provides insight into the nature of the relationships within the problem. Mastering this technique is essential for advancing in various branches of algebra and can be applied to real-world scenarios.
In this section, we will explore how to approach problems that require breaking down terms into manageable pieces. Through practice and understanding of the underlying principles, one can learn to identify patterns and apply the right techniques to achieve the desired result efficiently.
Understanding Quadratic Equations and Factoring
In algebra, certain types of problems involve expressions where a variable is raised to the second power. These expressions often contain multiple terms, and the challenge lies in simplifying them to identify their solutions. The key to handling such problems is breaking them down into smaller, more manageable components.
This process involves manipulating the expression to reveal its factors. Once the terms are separated, they can be worked with individually to uncover the values that satisfy the problem. By mastering this approach, it becomes easier to handle more complex scenarios and gain a deeper understanding of mathematical relationships.
Developing the ability to recognize patterns in these types of expressions is essential. With practice, one can learn to quickly identify the most efficient method for simplifying and solving these problems, applying the right techniques in various contexts.
Steps for Factoring Quadratic Equations
To simplify and solve expressions involving a variable raised to the second power, a methodical approach is required. Breaking down the expression into smaller components is the first step towards identifying the values that satisfy the given conditions. Understanding the sequence of actions to take ensures that each term is properly handled, leading to an accurate result.
Step 1: Identify Key Components
Begin by identifying the components of the expression. Typically, these include a constant term, a variable term, and a coefficient attached to the variable. Recognizing these elements helps to visualize the structure of the problem and determine the most effective strategy for simplification.
Step 2: Decompose the Expression
The next step involves breaking the expression into parts that can be multiplied to produce the original terms. This requires finding pairs of numbers or expressions that, when combined, will give the desired result. This step may involve trial and error, but with practice, it becomes more intuitive. Once the expression is properly decomposed, the values that satisfy the conditions will become clear.
Identifying the Correct Factoring Method
When tackling a problem that involves a variable raised to the second power, it’s essential to choose the right approach for simplifying the expression. There are different methods for breaking down such problems, and selecting the appropriate one depends on the structure of the expression. Each method has its strengths and is best suited for certain types of problems.
Method Selection Based on Structure

The first step in identifying the correct method is analyzing the structure of the expression. Common patterns often guide which technique to use. Here are some key considerations:
- If the expression contains a common factor across all terms, start by factoring out the greatest common divisor.
- If the expression fits a specific form, such as a perfect square or a difference of squares, apply the corresponding rule.
- If no obvious patterns emerge, consider trial and error with different factor pairs.
Recognizing Common Patterns
Over time, you will develop an ability to recognize common patterns, which will help you make faster decisions on which method to apply. Some typical forms include:
- Perfect Square Trinomial: Recognizable when the first and last terms are perfect squares, and the middle term is twice the product of their square roots.
- Difference of Squares: Identified when the expression consists of two perfect squares separated by a minus sign.
- Simple Trinomial: When the middle term is the sum or difference of two terms, you can factor it into two binomials.
Common Mistakes in Factoring Quadratics
While simplifying expressions involving a variable raised to the second power, many people make recurring mistakes that can lead to incorrect results. Recognizing these common errors is crucial in improving accuracy and ensuring that the proper methods are applied. By understanding what often goes wrong, it’s easier to avoid these pitfalls and approach the problem more effectively.
Overlooking Common Factors
One of the most frequent mistakes is neglecting to identify and factor out the greatest common factor (GCF) from all terms in the expression. This step is essential before proceeding with further simplification. Skipping it can result in a more complicated problem and incorrect results.
- Always check if there is a common factor before proceeding with other methods.
- Factor out the GCF to simplify the expression as much as possible.
Incorrectly Pairing Factors

Another mistake occurs when choosing the wrong pair of numbers to break down the expression. This error can happen when trying to find two numbers that multiply to give a specific product but fail to add up to the correct sum. Identifying the right pair is key to correctly simplifying the expression.
- Ensure that the sum and product of the factor pair match the terms in the original expression.
- Check your work to verify that the selected numbers satisfy both conditions.
Forgetting to Check the Solution
After simplifying, it’s important to verify that the result is correct. A common mistake is to assume that the problem is solved once the factors are identified. However, testing the solution by expanding the factored expression can catch errors and confirm the accuracy of the result.
- Always check your final answer by multiplying the factors back together.
- If the result doesn’t match the original expression, revisit the steps for errors.
Recognizing the Key Terms in Equations
In algebraic problems involving expressions with variables raised to the second power, identifying the key components is essential for simplifying the problem and finding the correct solution. Understanding how different parts of the expression relate to each other can guide the method you choose for simplifying and solving the problem.
Identifying the Coefficients and Constants

The first step in breaking down these problems is recognizing the role of each term in the expression. The coefficient is the number that multiplies the variable, and the constant term is the number without a variable. Recognizing these elements allows you to determine the necessary approach to simplify the expression.
- The coefficient of the variable determines how the terms are grouped.
- The constant term often provides insight into possible factor pairs.
Recognizing Patterns in the Expression
Many expressions follow common patterns that can be easily recognized with practice. For example, if the expression consists of two terms that are perfect squares, or if there is a difference between two terms, these patterns often indicate a specific method of simplification. Recognizing these patterns early helps you determine the best approach quickly.
- Perfect squares often signal the use of special binomial identities.
- Differences between squares suggest the application of the difference of squares method.
Example Problems Solved Using Factoring
To understand how to simplify and solve expressions involving variables raised to the second power, it’s helpful to look at a few example problems. By applying the correct methods, these problems can be broken down into manageable parts, allowing us to find the solutions step by step. The following examples demonstrate how to approach such problems and apply the appropriate strategies.
Example 1: Simplifying a Basic Expression
Consider the following problem where the goal is to simplify the expression and find the values that satisfy the conditions:
| Expression | Steps | Solution |
|---|---|---|
| x² + 5x + 6 | 1. Identify factors of 6 that sum to 5 (2 and 3). 2. Split the middle term using these values. 3. Factor the expression: (x + 2)(x + 3). |
x = -2, x = -3 |
Example 2: Dealing with Larger Coefficients
This example shows how to handle an expression with larger coefficients. Notice the difference in approach when the numbers become larger or more complex:
| Expression | Steps | Solution |
|---|---|---|
| 2x² + 7x + 3 | 1. Identify factors of (2 * 3 = 6) that sum to 7 (6 and 1). 2. Split the middle term using these values. 3. Factor the expression: (2x + 1)(x + 3). |
x = -1/2, x = -3 |
These examples highlight the process of breaking down the expression and identifying the key factors. By practicing with similar problems, one can become more efficient in simplifying and finding solutions to such problems.
How to Factor Simple Quadratic Equations
When working with expressions involving a variable raised to the second power, the goal is often to simplify the expression and find the values that satisfy the conditions. For simpler problems, the process becomes more straightforward, requiring only basic steps to break the expression into manageable parts. The key is to recognize the components and apply the right approach to simplify them.
Step-by-Step Process
To factor a simple expression of this type, follow these steps:
- Identify the key terms: Look at the expression and identify the coefficient of the variable and the constant term. For example, in the expression x² + 5x + 6, the coefficient is 1, the variable term is 5x, and the constant is 6.
- Find factor pairs of the constant: Find pairs of numbers that multiply to the constant term and add up to the coefficient of the variable term. In this case, the factors of 6 that add to 5 are 2 and 3.
- Rewrite the middle term: Split the middle term based on the factor pair identified. This means x² + 2x + 3x + 6.
- Group terms: Group the terms in pairs. For the example, group (x² + 2x) and (3x + 6).
- Factor out the common terms: In each group, factor out the greatest common factor. For example, x(x + 2) and 3(x + 2).
- Factor the binomial: Combine the common binomial factor to get the final factored expression: (x + 2)(x + 3).
Example
Let’s apply this method to a specific example:
- Expression: x² + 7x + 10
- Factors of 10 that add to 7: 5 and 2
- Rewrite the middle term: x² + 5x + 2x + 10
- Group terms: (x² + 5x) + (2x + 10)
- Factor common terms: x(x + 5) + 2(x + 5)
- Combine common factors: (x + 5)(x + 2)
This process can be applied to any simple expression of this type. By practicing with different examples, it becomes easier to spot the factors and simplify the expression efficiently.
Why Factoring is Important in Algebra
In algebra, breaking down complex expressions into simpler components is a key skill. This process allows us to gain a deeper understanding of how different elements in an expression interact. By simplifying problems into their most basic forms, we can identify the roots or solutions more easily, making the process faster and more efficient.
Improving Problem Solving Efficiency
When we decompose an expression, we can quickly identify patterns and simplify the steps required to find a solution. This method not only saves time but also reduces the complexity of larger problems.
- Speeds up the process of finding the roots or values that satisfy the expression.
- Reduces the need for trial and error or more complex techniques.
- Helps in recognizing common patterns and relationships between terms.
Building Stronger Mathematical Foundations
Mastering the process of breaking down expressions into simpler components also strengthens overall mathematical skills. It promotes logical thinking and a deeper understanding of mathematical relationships, which is crucial for tackling more advanced problems.
- Develops a solid foundation for other areas of algebra and mathematics.
- Helps improve analytical skills and understanding of mathematical structures.
- Facilitates better understanding of complex concepts as students progress.
Overall, learning to break down and simplify expressions is not just about solving one problem–it’s about building the skills needed to approach a wide range of challenges in mathematics.
Exploring Different Factoring Techniques
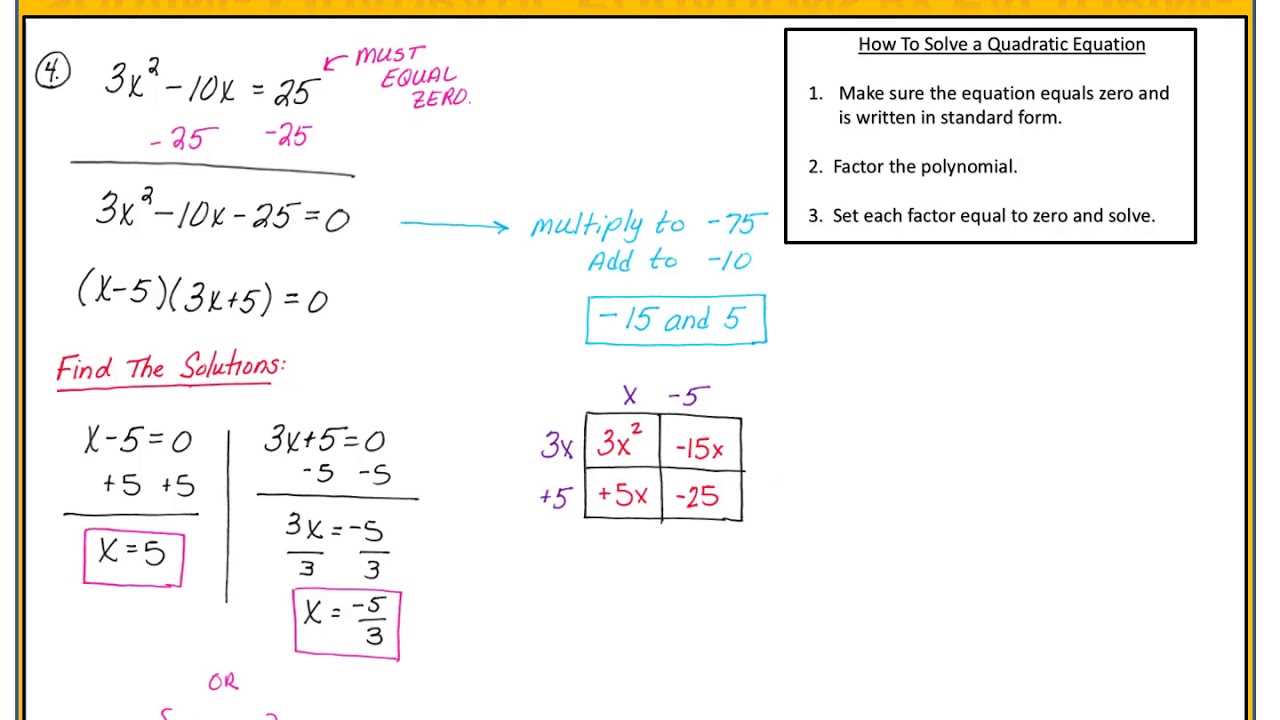
There are several approaches to simplify and decompose mathematical expressions, each suited to different types of problems. Understanding these techniques enables us to approach expressions from various angles, ultimately making the process of identifying solutions more efficient. Below, we will explore some of the most common methods and when to apply them.
1. The Trial and Error Method
This technique involves guessing pairs of numbers that multiply to the constant term and add up to the middle coefficient. Although not as structured as other methods, it is effective for simpler expressions.
| Expression | Steps | Solution |
|---|---|---|
| x² + 7x + 10 | 1. Identify factors of 10 that add up to 7: 5 and 2. 2. Write the expression as (x + 5)(x + 2). |
x = -5, x = -2 |
2. The Grouping Method
The grouping method involves splitting the middle term into two parts, making it easier to factor by grouping. This is especially useful when the coefficients of the terms are larger or more complex.
| Expression | Steps | Solution |
|---|---|---|
| 2x² + 7x + 3 | 1. Identify factors of 6 (2 * 3) that add to 7: 6 and 1. 2. Split the middle term: 2x² + 6x + x + 3. 3. Group and factor: 2x(x + 3) + 1(x + 3). |
x = -3/2, x = -1 |
Both methods are valuable tools for simplifying and solving problems involving terms with variables raised to the second power. While the trial and error method works well for basic problems, grouping is more effective for more complex expressions with larger coefficients.
Advanced Factoring Methods for Quadratics
As mathematical expressions become more complex, simpler methods may not be sufficient to break them down efficiently. Advanced techniques offer more systematic and precise approaches for simplifying and identifying the components of these expressions. In this section, we will explore some of the more advanced strategies that are commonly used in these types of problems.
Using the Difference of Squares
The difference of squares is a powerful tool for simplifying expressions that involve the subtraction of two squared terms. It works under the principle that the difference between two squares can always be factored as the product of their sum and difference.
- Formula: a² – b² = (a + b)(a – b)
- Example: x² – 16 = (x + 4)(x – 4)
Working with Perfect Square Trinomials

Perfect square trinomials are expressions that can be factored into the square of a binomial. Recognizing these types of expressions helps simplify the process of finding their roots or components.
- Formula: a² + 2ab + b² = (a + b)²
- Example: x² + 6x + 9 = (x + 3)²
Both methods require careful analysis of the expression’s structure to identify when they apply. These advanced methods streamline the process of breaking down complex terms, making it easier to find the solutions.
Understanding the Role of the Discriminant
In many algebraic problems, especially when dealing with second-degree expressions, the discriminant plays a crucial role in determining the nature of the solutions. It provides insight into whether the solutions are real, complex, or repeated, allowing us to assess the type of results we can expect without solving the problem completely. Understanding how to interpret the discriminant can save time and guide the approach to finding the roots of the expression.
The discriminant is part of the general formula used to find the roots, but its value alone can offer valuable information about the solutions:
- Positive discriminant: Two distinct real roots exist.
- Zero discriminant: Exactly one real root exists, indicating repeated solutions.
- Negative discriminant: No real roots exist, but there are two complex roots.
By examining the discriminant, we can make immediate conclusions about the number and type of solutions, helping to determine the appropriate method to proceed with.
Checking Your Work After Factoring

Once you’ve broken down a complex expression into simpler parts, it’s essential to verify the correctness of your work. This step ensures that the simplification process was accurate and that the results are reliable. Double-checking your process can help you avoid mistakes and confirm that the factors you’ve found truly match the original expression.
One effective method of verification is to expand or multiply the factors you obtained and compare them to the original expression. If the expanded form matches the starting expression, you’ve done the work correctly. If not, it’s time to revisit your steps.
- Step 1: Multiply the terms in the factors.
- Step 2: Compare the expanded result with the original expression.
- Step 3: Check for signs, coefficients, and constant terms.
By following this verification process, you can be confident that the factorization is correct and that your final result is valid. A small mistake in the early steps can lead to incorrect results, so taking the time to check is crucial for accurate solutions.
Verification Using the Quadratic Formula
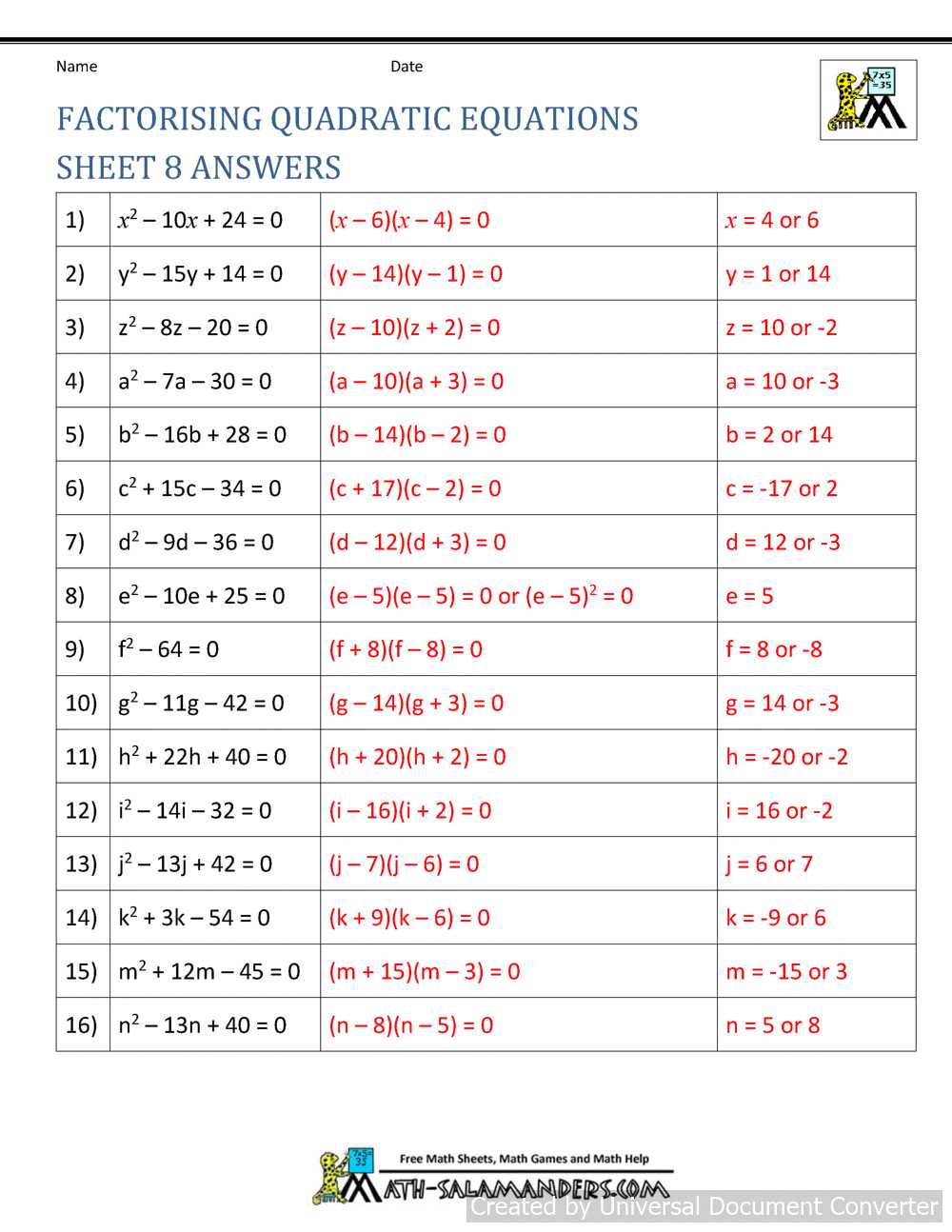
After simplifying an expression into its factors, it’s essential to verify the results to ensure accuracy. One reliable method of verification is using the quadratic formula, which provides a direct way to find the roots of any expression in this form. By comparing the solutions derived from both methods, you can confirm the correctness of your factorization process.
The quadratic formula is expressed as:
x = (-b ± √(b² – 4ac)) / 2a
To verify your factorized expression, substitute the values of the coefficients from the original expression into the quadratic formula and solve for x. If the solutions match the roots obtained through factorization, you can be confident that your work is correct. This method serves as an effective cross-check to ensure no errors were made in the earlier steps.
Remember that the discriminant (b² – 4ac) in the quadratic formula will tell you how many real or complex roots the expression has. This can provide additional insight into the accuracy of your results.
Real-World Applications of Factoring
Breaking down complex expressions into simpler components is not just useful in mathematics, but has practical applications in many fields. From engineering and computer science to finance and physics, the ability to simplify expressions plays a crucial role in solving real-world problems. By understanding how to break down relationships and structures, you can solve a variety of problems more efficiently.
Engineering and Design
In engineering, factoring is used to analyze and design systems, such as optimizing structures and analyzing forces. For instance, when determining the stresses on beams or analyzing fluid dynamics, engineers often encounter expressions that need to be simplified for easier calculation and understanding. Factoring helps break these expressions down to make complex designs more manageable.
Finance and Economics
In the world of finance, factoring is applied in situations like calculating returns on investments, optimizing profit margins, or breaking down complex cost functions. By simplifying expressions, financial analysts can create more accurate models and forecasts. Whether it’s evaluating the break-even point of a business or calculating interest over time, the ability to manipulate and simplify algebraic expressions is essential for making informed decisions.
Understanding how to simplify mathematical relationships gives professionals in various industries a powerful tool for making better decisions and solving complex problems. Whether you’re analyzing trends, optimizing designs, or creating financial models, the skill of breaking down expressions is an invaluable resource.
Using Factoring in Engineering and Physics
The ability to break down complex expressions into simpler components is fundamental in both engineering and physics. These fields often require working with mathematical models that describe physical systems, and simplifying those models makes it easier to solve for unknowns, optimize designs, and predict behaviors. Factoring plays a key role in simplifying equations, allowing for more efficient calculations and clearer understanding of systems.
Applications in Engineering
In engineering, simplifying expressions helps solve problems related to forces, stresses, and material properties. Some examples where simplification is crucial include:
- Structural Analysis: Engineers often need to simplify equations to analyze forces on beams, columns, and other structures.
- Electrical Circuits: Simplifying equations can help engineers determine the current, resistance, or voltage across components in a circuit.
- Thermal Systems: In heat transfer analysis, simplifying heat flow equations can lead to more accurate predictions of system performance.
Applications in Physics

In physics, the simplification of equations is essential to solving problems related to motion, energy, and other fundamental concepts. Here are a few specific uses:
- Projectile Motion: Equations describing the motion of objects under gravity often need to be simplified to calculate the time of flight, range, and maximum height.
- Energy Conservation: In energy transfer equations, simplifying terms can help clarify relationships between potential and kinetic energy.
- Electricity and Magnetism: Simplified equations help analyze the behavior of electric fields, currents, and magnetic forces.
In both engineering and physics, breaking down complex mathematical expressions into simpler forms makes problem-solving more straightforward. It not only helps with calculations but also aids in the visualization and understanding of physical systems, leading to better-designed structures, more efficient technologies, and improved scientific models.
Solving Word Problems with Factoring
When dealing with word problems, the key is to transform the given information into a mathematical expression that represents the scenario. By simplifying this expression, one can often find the unknowns. These problems can involve a variety of real-world situations, from areas of geometric shapes to relationships between quantities. The ability to break down these relationships into solvable parts helps in finding solutions efficiently.
Example Problem 1: Area of a Rectangle

Consider a problem where you are given the area of a rectangular garden and the length is 3 meters more than its width. To find the dimensions, we first set up an expression for the area:
| Expression | Meaning |
|---|---|
| Length = x + 3 | Length is 3 meters more than width |
| Area = x(x + 3) | Area is length multiplied by width |
Now, the equation becomes:
| Step | Expression |
|---|---|
| Set up equation | x(x + 3) = 36 |
| Expand and simplify | x2 + 3x = 36 |
| Rearrange | x2 + 3x – 36 = 0 |
From here, we can simplify the equation and find the value of x, which represents the width of the garden. Once we have the width, the length can be determined easily.
Example Problem 2: Product of Two Numbers
Let’s take another example: two numbers multiply to 45 and add up to 14. The relationship between these numbers can be expressed as:
| Expression | Meaning |
|---|---|
| Product = x(x + 14) | The two numbers multiply to 45 |
We can now translate this information into a solvable mathematical problem and determine the values of x and its corresponding number.
Through the process of simplifying the expressions and solving for the unknowns, we can apply mathematical techniques to real-world situations, helping us make sense of complex scenarios.
Approaching Word Problems Step-by-Step
When tackling word problems, it’s essential to break down the situation into manageable parts. Rather than trying to solve everything at once, focus on understanding the scenario, identifying the key relationships, and translating them into mathematical expressions. By following a structured approach, you’ll be able to simplify even the most complex problems and find the solution with clarity and confidence.
Step 1: Understand the Problem
The first step is to read the problem carefully and identify the key information. Look for numbers, units, and any relationships between variables. Pay attention to phrases that indicate operations, such as “more than,” “less than,” or “increased by.” These terms will help you set up the correct mathematical expressions.
Step 2: Translate the Information
Once you’ve identified the important details, the next step is to translate them into mathematical terms. For example, if the problem describes a relationship between two quantities, express that relationship using variables. If the problem provides a total value, such as an area or perimeter, write that in terms of the variables involved.
For instance, if you’re asked to find the length and width of a rectangle where the length is 5 meters more than the width, you might let x represent the width, and the length would then be expressed as x + 5.
Step 3: Set Up the Mathematical Model

Now that you have the relationships between the quantities, form an equation or system of equations. This step involves translating the word problem into a solvable mathematical expression. Ensure that all the key elements are included, and that the equation accurately reflects the problem’s conditions.
For example, if the problem gives you the area of the rectangle, say 60 square meters, you would write the equation as:
| Expression | Meaning |
|---|---|
| Area = Length × Width | Area is the product of length and width |
| 60 = (x + 5) × x | The area is 60, and length is x + 5 |
Step 4: Solve the Mathematical Model
Once you’ve set up the equation, apply the appropriate methods to solve it. This may involve expanding, simplifying, and isolating the variable to find the solution. If necessary, use the methods you’ve learned to find the value of the unknowns, whether it’s through algebraic manipulation or applying numerical techniques.
By following these steps, you can confidently approach any word problem, breaking it down into its core components and using mathematical methods to find the solution.
Factoring Without Trial and Error
When working with algebraic expressions, it’s essential to use a structured approach instead of relying on guesswork. By identifying patterns and using a step-by-step method, you can break down complex expressions efficiently without testing random possibilities. Understanding the relationships between the terms allows for accurate and quick factorization.
Identifying Key Components
The first step is to recognize the structure of the expression you’re dealing with. For a common form such as ax² + bx + c, you need to find two values that multiply to a * c and add up to b. This is a critical part of breaking the expression into simpler components, which can then be factored without trial and error.
Using the “ac Method” for Efficient Factorization
One of the most reliable strategies for factorization is the “ac method.” This method helps to eliminate guesswork by focusing on the relationship between the leading coefficient a and the constant c. By multiplying these two values together, you get a product, and your task is to find two numbers that multiply to this product and add to the middle coefficient b.
For example, consider the expression:
| Expression | Explanation |
|---|---|
| 6x² + 11x – 35 | Here, a = 6, b = 11, and c = -35. |
Start by multiplying a and c: 6 * -35 = -210. Now, find two numbers that multiply to -210 and add to 11. These numbers are 21 and -10, since 21 * -10 = -210 and 21 + (-10) = 11.
Breaking Down and Simplifying
Now, rewrite the expression using the two numbers you found:
6x² + 21x – 10x – 35
Next, group the terms:
(6x² + 21x) – (10x + 35)
Factor out the greatest common factor (GCF) from each group:
3x(2x + 7) – 5(2x + 7)
Finally, factor out the common binomial:
(3x – 5)(2x + 7)
By following this method, you can factor expressions without trial and error, ensuring a systematic and accurate approach every time.