
For students preparing for the AP Calculus BC test, understanding the core concepts and problem-solving strategies is crucial. This section provides detailed solutions to the most challenging questions, focusing on techniques that can improve your understanding and performance. By breaking down each problem, you can gain valuable insights into how to approach similar questions in the future.
Mastering the material requires more than just memorizing formulas; it involves applying critical thinking and reasoning skills to complex mathematical scenarios. Throughout this article, you will find step-by-step guides that illustrate how to navigate through various types of problems, from differential equations to integrals, and even advanced topics involving series and sequences.
With a clear breakdown of the problem-solving process, students can sharpen their ability to identify key components in each question and develop an organized approach to finding the correct solutions. Whether you are revising for a final test or seeking to improve your calculus skills, this guide will offer the tools you need to succeed.
AP Calc BC 2012 Exam Answers
In this section, we will explore detailed solutions for a selection of questions from the advanced calculus test, helping you to grasp the underlying concepts and techniques needed to tackle similar problems. These solutions cover a variety of topics, offering comprehensive steps that guide you through the reasoning process.
The goal is to break down complex problems into manageable parts, explaining each step clearly. By reviewing these examples, students can learn effective strategies for problem-solving and enhance their mathematical thinking. From integration methods to differential equations, this section aims to provide clarity on the key skills needed for success.
By understanding the structure of each question and how to approach them methodically, students can build confidence in their abilities and improve their overall performance in future assessments. Each solution presented is carefully explained to ensure that the principles behind each step are easy to follow and apply to other types of problems.
Overview of the AP Calc BC 2012 Exam

This section provides an overview of the advanced mathematics assessment that tests a range of topics covered in a college-level calculus course. The focus is on evaluating students’ ability to apply mathematical concepts in solving complex problems. The test includes multiple-choice questions and free-response sections designed to assess both theoretical knowledge and practical problem-solving skills.
Key Areas Tested
The assessment covers various topics such as limits, derivatives, integrals, and series. Students are expected to demonstrate their understanding of these concepts and their ability to solve problems involving these principles. Emphasis is placed on critical thinking and the ability to approach problems systematically.
Scoring and Time Management
Students are allocated a specific amount of time to complete the test, requiring effective time management to ensure all questions are addressed. The test is graded on a scale that reflects the level of mastery achieved in each area. Understanding the format and the weighting of each section helps in planning an efficient approach to tackling the questions.
Key Topics Covered in the 2012 Exam
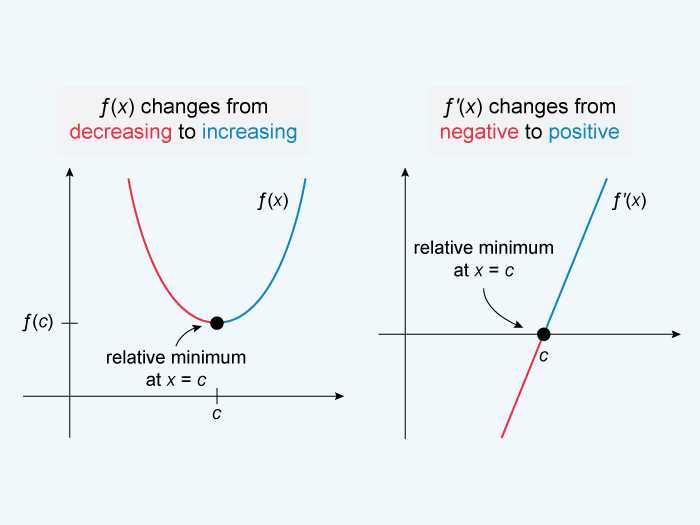
This section highlights the major mathematical concepts assessed during the advanced level assessment. The topics range from fundamental principles of calculus to more complex theories, all of which require deep understanding and the ability to apply them in various scenarios. Mastery of these topics is essential for achieving high marks in the test.
Limits and Continuity
One of the primary areas covered is the study of limits and the continuity of functions. Students are expected to demonstrate their understanding of how functions behave near specific points and the importance of limits in defining derivatives and integrals. Problems in this section test both theoretical understanding and practical application of these concepts.
Integration and Series

The assessment also delves into advanced topics such as integration techniques and infinite series. Students are required to solve problems involving both definite and indefinite integrals, as well as series convergence tests. Understanding these areas is critical for solving more complex mathematical problems that arise in real-world applications.
Understanding the Free Response Questions
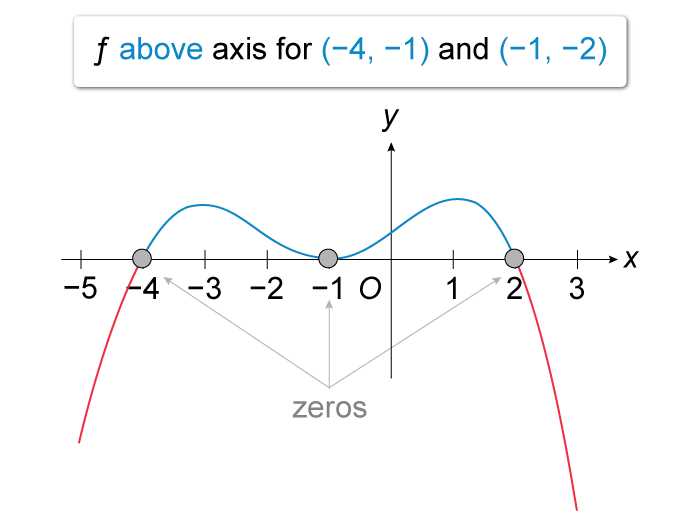
The free response section of the test is designed to assess a student’s ability to apply mathematical concepts to solve complex problems. Unlike multiple-choice questions, these problems require students to show their work and provide a detailed explanation of the steps taken to reach the solution. The ability to clearly communicate the reasoning behind each step is as important as finding the correct answer.
Each problem is typically broken down into parts, testing various aspects of the topic at hand. It’s essential to approach these questions methodically, ensuring that all parts are addressed and explained thoroughly.
Key Strategies for Tackling Free Response Questions
- Read the Question Carefully: Pay attention to all parts of the problem and ensure you understand what is being asked before starting your solution.
- Show All Work: Always provide detailed steps, even if you can solve the problem in your head. This helps to demonstrate your understanding and can earn partial credit.
- Focus on Organization: Structure your response clearly, breaking down complex calculations into smaller, manageable steps.
- Use Proper Notation: Proper mathematical notation and formatting are essential for clarity and precision.
Common Pitfalls to Avoid
- Skipping Steps: Even if the solution seems simple, always show how you arrived at each conclusion.
- Not Answering All Parts: Ensure that every part of the question is answered, as failing to do so can lead to lost points.
- Overcomplicating the Solution: Aim for simplicity and clarity–long-winded or convoluted answers can confuse graders.
Multiple Choice Section Insights
The multiple-choice section of the test is designed to assess a student’s quick problem-solving ability and understanding of key concepts in advanced mathematics. This portion tests not only knowledge but also the ability to select the correct answer efficiently, often under time constraints. It is important to have a strong grasp of the material and be able to quickly identify the most suitable method for each problem.
Success in this section depends on both accuracy and speed. Students are often faced with problems that require a balance between theoretical knowledge and practical application. While the correct answer is key, understanding why it is the correct choice is just as important.
Effective Strategies for Multiple Choice Questions
- Eliminate Wrong Answers: If unsure about the correct answer, try to rule out the clearly incorrect options first. This increases your chances of selecting the correct one.
- Read Carefully: Even though these questions are brief, it is important to read each one thoroughly to ensure you understand the problem before making a choice.
- Work Backwards: In some cases, starting with the answer choices and working backward to check the solution can be an effective strategy.
- Manage Time Wisely: Allocate time wisely, ensuring you don’t spend too much time on any single question. If unsure, move on and come back if time allows.
Common Pitfalls to Avoid
- Overthinking: Multiple-choice questions are often designed to test your ability to recognize the correct answer quickly, so don’t overcomplicate the process.
- Rushing: While time is limited, rushing through questions can lead to careless mistakes. Take a moment to ensure your answer makes sense.
- Skipping Questions: Avoid skipping questions without attempting them, as guessing later can sometimes be better than leaving them unanswered.
Tips for Solving AP Calc Problems
Solving advanced mathematics problems requires both a solid understanding of the concepts and the ability to apply them efficiently. Developing a systematic approach to problem-solving can help you tackle even the most challenging questions with confidence. Whether working through integrals, derivatives, or series, having a strategy in place is key to ensuring accuracy and clarity in your solutions.
Key Strategies for Success
- Understand the Problem First: Carefully read through the question and identify the key information. Clarify what is being asked before jumping into calculations.
- Organize Your Work: Break down complex problems into smaller, manageable steps. Showing each step helps prevent errors and makes it easier to follow your thought process.
- Check Units and Notation: Ensure all units are consistent and that you are using correct mathematical notation throughout the solution.
- Use Visual Aids: Graphs, tables, and diagrams can be very helpful in understanding the problem and visualizing the relationships between variables.
Common Mistakes to Avoid
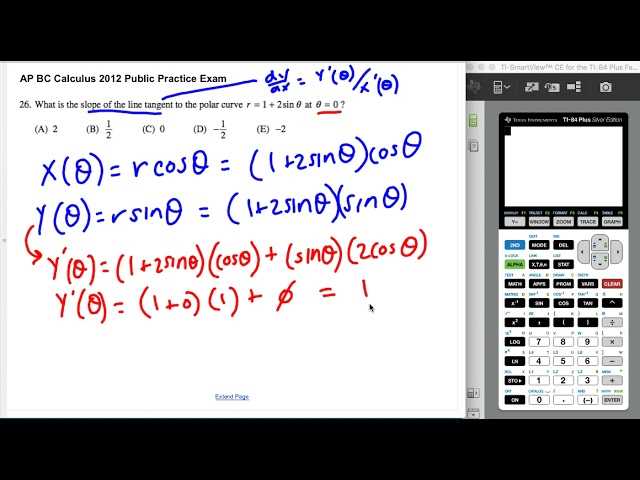
- Skipping Steps: Avoid skipping intermediate steps, even if you are confident in your answer. Each step helps solidify your understanding and reduces the risk of mistakes.
- Misapplying Formulas: Make sure you are applying the correct formula for the given problem and that all variables are defined properly.
- Not Double-Checking: Take the time to check your solution for errors, especially in complex calculations where small mistakes can lead to incorrect results.
Step-by-Step Solutions to Exam Problems
In this section, we will break down several challenging problems from the advanced mathematics assessment and provide detailed, step-by-step solutions. The purpose is to show how to approach each problem methodically, ensuring that every step is clearly explained. By understanding the reasoning behind each solution, students can improve their problem-solving skills and apply these strategies to other questions.
Example 1: Solving an Integral
In this example, we will work through the process of solving a definite integral. The key to solving such problems is understanding the appropriate method for integration and carefully applying it to find the correct solution.
- Step 1: Identify the integral’s bounds and the function to be integrated.
- Step 2: Choose the appropriate integration technique (e.g., substitution, integration by parts, or direct integration).
- Step 3: Perform the integration and simplify the result.
- Step 4: Evaluate the integral at the bounds and calculate the final answer.
Example 2: Solving a Differential Equation
For solving a differential equation, we’ll use separation of variables. This is a common method for first-order differential equations, and it involves isolating the variables to integrate each side of the equation.
- Step 1: Rearrange the equation to separate variables on opposite sides.
- Step 2: Integrate both sides of the equation with respect to their respective variables.
- Step 3: Solve for the dependent variable by isolating it on one side of the equation.
- Step 4: Apply initial conditions (if provided) to find the particular solution.
Common Mistakes to Avoid in Calculus
When working through advanced mathematical problems, there are several common pitfalls that students often encounter. These mistakes can lead to incorrect answers and wasted time. Recognizing and avoiding them is crucial for improving both accuracy and efficiency. In this section, we will highlight some of the most frequent errors made in calculus and provide tips on how to prevent them.
Misapplication of Rules
One of the most common mistakes is incorrectly applying mathematical rules or formulas. It is important to ensure that the right rule is used for the given problem. Whether it’s applying the power rule incorrectly or mixing up the product and quotient rules, these small errors can lead to major mistakes in the final solution.
- Example: Using the wrong formula for integration or differentiation can result in incorrect answers. Always verify that the rule is appropriate for the specific type of function you’re working with.
Ignoring Boundary Conditions
Another frequent error is overlooking the boundary conditions, especially in definite integrals and differential equations. Boundary conditions are essential for determining the precise solution to a problem, and neglecting them can lead to incomplete or inaccurate answers.
- Example: In a definite integral, forgetting to evaluate the function at the limits will result in an incorrect value for the integral.
How to Approach Calculus Word Problems
Word problems in advanced mathematics can often seem intimidating at first, as they involve translating real-world situations into mathematical expressions. However, with the right approach, these problems become much more manageable. The key is to break the problem down into smaller, more understandable steps, allowing you to identify the appropriate techniques and methods for solving it.
The first step is to carefully read through the problem, making sure to highlight key information, such as variables, rates, or any other data that might be needed. Once you understand what is being asked, the next step is to decide which mathematical principles apply to the problem. This could include concepts such as optimization, related rates, or calculating areas and volumes.
Step-by-Step Approach
- Identify Given Information: Carefully note down the data provided in the problem, such as initial conditions, rates, or dimensions.
- Define Variables: Assign variables to the unknowns in the problem, making sure they are clearly labeled to avoid confusion.
- Choose the Right Technique: Determine which method–such as differentiation, integration, or setting up equations–will help solve the problem.
- Set Up the Equation: Translate the word problem into a mathematical equation that represents the relationships between the variables.
Final Steps
- Solve the Equation: Apply the appropriate mathematical operations to solve for the unknowns.
- Interpret the Result: Ensure the solution makes sense in the context of the problem and is presented in the correct units or format.
- Verify Your Answer: Double-check your work to ensure no steps were skipped or misunderstood.
Essential Calculus Formulas for the Exam

Having a solid grasp of fundamental mathematical formulas is crucial for successfully solving problems in advanced mathematics. These formulas serve as the building blocks for solving a variety of problems, from differentiation to integration and beyond. In this section, we will review the most essential formulas that you should be familiar with, as they will help you approach problems efficiently and with confidence.
| Formula | Description |
|---|---|
| Power Rule | If f(x) = x^n, then f'(x) = n * x^(n-1). |
| Product Rule | If f(x) = g(x) * h(x), then f'(x) = g'(x) * h(x) + g(x) * h'(x). |
| Quotient Rule | If f(x) = g(x) / h(x), then f'(x) = (g'(x) * h(x) – g(x) * h'(x)) / (h(x))^2. |
| Chain Rule | If f(x) = g(h(x)), then f'(x) = g'(h(x)) * h'(x). |
| Fundamental Theorem of Calculus | If F(x) is the antiderivative of f(x), then ∫[a,b] f(x) dx = F(b) – F(a). |
| Integration by Parts | ∫ u dv = uv – ∫ v du. |
| Substitution Rule | If u = g(x), then ∫ f(g(x)) g'(x) dx = ∫ f(u) du. |
Using the Calculator Efficiently During the Exam
Effective use of the calculator during a mathematics assessment can significantly improve efficiency, allowing you to focus on problem-solving rather than lengthy calculations. It is important to understand the functionalities of the calculator and how they can be applied to different types of problems. While the tool is valuable, it is crucial to strike a balance between relying on it and ensuring that key mathematical concepts are understood and applied correctly.
Begin by familiarizing yourself with the calculator’s advanced features, such as graphing capabilities, derivative and integral functions, and table generation. These features can save valuable time, especially when dealing with complex functions or large datasets. However, it is equally important to use the calculator strategically, ensuring that it complements your mathematical reasoning rather than replaces it.
Before the assessment, practice using the calculator in different scenarios to get comfortable with its functions. This will help you quickly adapt during the test, making it easier to navigate between different modes, input functions, and interpret results accurately.
Interpretation of Graphs and Tables
Interpreting visual data, such as graphs and tables, is a crucial skill in advanced mathematics. These representations offer a concise way to understand relationships between variables and help in analyzing patterns, trends, and behaviors. By carefully examining the information presented, you can extract valuable insights that guide problem-solving and provide a clearer understanding of the underlying concepts.
When dealing with graphs, focus on the key features such as intercepts, slopes, and asymptotes. Understanding how the graph behaves at different points allows you to make inferences about the function it represents. For example, identifying the maximum and minimum values of a function or determining its concavity can provide important information for solving related problems.
Tables, on the other hand, are often used to present discrete data. Pay attention to the structure of the table, and be sure to recognize patterns or trends in the values. For instance, if the table represents a sequence, recognizing the rate of change between successive terms can help in formulating the appropriate mathematical approach to solve a problem.
Preparation Strategies for the AP Calc BC Exam
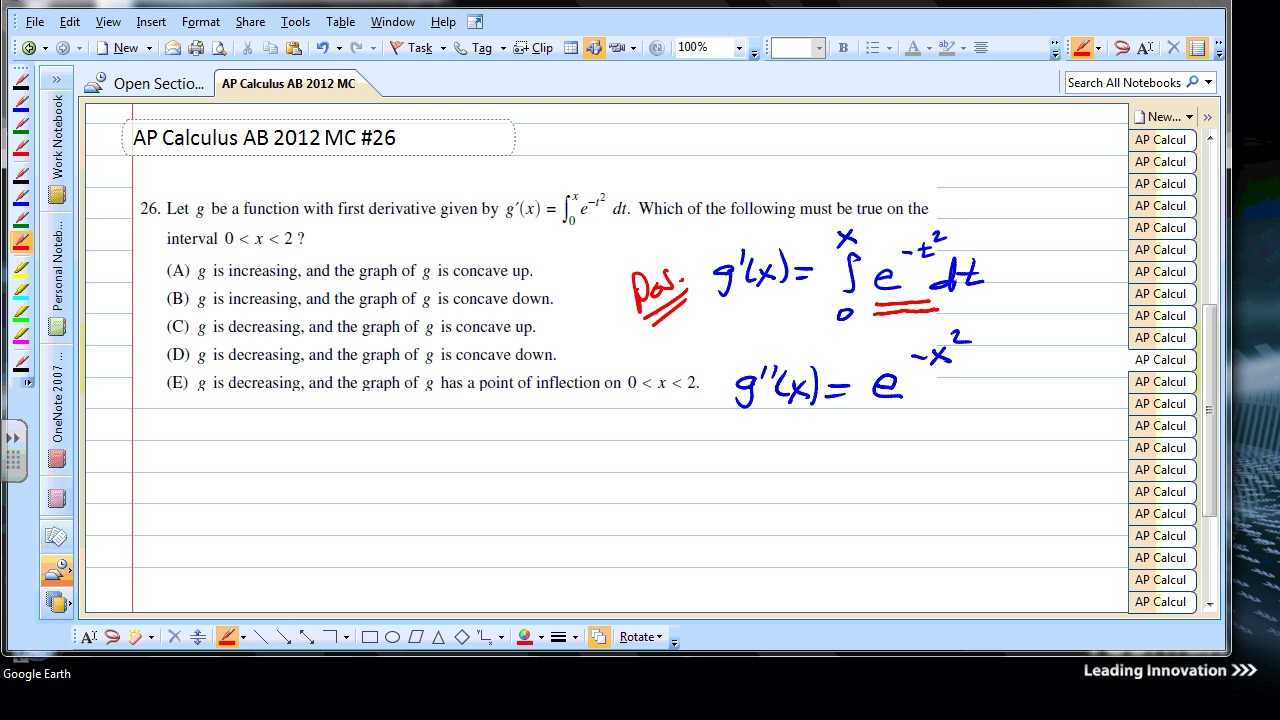
Effective preparation for a high-level mathematics assessment requires a combination of understanding the content, practicing problem-solving techniques, and familiarizing oneself with the test format. To succeed, it is important to not only master the core concepts but also to develop strategies for managing time and stress during the test. Below are several tips to help you prepare efficiently and confidently for the assessment.
Mastering Core Concepts
Before diving into practice problems, ensure that you have a solid grasp of the fundamental topics. A deep understanding of key concepts will allow you to approach problems with confidence. Focus on the following areas:
- Functions and Graphs: Understand how to interpret and manipulate various types of functions, including polynomials, rational functions, and exponential functions.
- Derivatives and Integrals: Be comfortable applying differentiation and integration techniques to solve problems involving rates of change and areas under curves.
- Sequences and Series: Be prepared to work with sequences, series, and convergence tests.
- Applications: Practice applying concepts to real-world problems, such as optimization, motion, and related rates.
Effective Practice and Time Management
In addition to understanding the material, practice is key to performing well. Work through practice problems from previous assessments, and be sure to simulate exam conditions to improve time management.
- Timed Practice: Set aside time for timed practice sessions to familiarize yourself with the pacing of the test. This will help you get used to solving problems efficiently under time constraints.
- Focus on Weak Areas: After each practice session, identify areas where you struggled and focus your efforts on improving those skills.
- Review Mistakes: Carefully review each mistake to understand where your reasoning went wrong and correct any misunderstandings.
By building a strong foundation in the core topics, practicing regularly, and refining your time management skills, you will be well-prepared for the assessment and equipped to perform at your best.
Time Management Tips for the Exam
Efficient time management is essential for performing well in a high-stakes test. Being able to allocate your time wisely during the assessment can make the difference between completing all questions and leaving some unanswered. With proper planning and practice, you can optimize your performance and avoid feeling rushed. Below are some strategies to help you manage your time effectively during the test.
Prioritize and Strategize
Begin by carefully analyzing the structure of the test to understand how to allocate your time most effectively. Consider the following tips:
- Read through the entire test: Quickly skim through the questions to get a sense of which sections may take more time and which are relatively easier. This will help you plan how to distribute your time across the test.
- Start with easier questions: Tackle the questions you feel most confident about first. This allows you to secure those points quickly and builds momentum for the more challenging questions.
- Estimate time for each section: Divide your available time according to the number of questions. Be sure to allocate more time to the more complex sections while leaving time for a final review.
During the Test
Once you are in the test, managing your time in real-time is key. Use the following strategies to ensure you are staying on track:
- Time limits for each question: Set a time limit for each question or section. If you find yourself stuck on a question, move on and return to it later if time allows.
- Don’t get bogged down: It’s easy to get frustrated with a challenging problem, but spending too much time on one question can cost you valuable minutes. Move forward if needed and come back later.
- Use the last few minutes wisely: Reserve the final moments of the test to quickly review your answers and ensure that you have filled in all the answers. Double-check for any mistakes or incomplete sections.
By carefully planning your approach and adhering to time limits for each section, you can ensure that you stay on track and maximize your performance during the test.
Practice with Past Exam Papers

One of the most effective ways to prepare for any high-level assessment is to practice with previous years’ materials. By reviewing and working through past tests, you gain a better understanding of the question format, time constraints, and key topics that tend to appear frequently. In this section, we will explore the benefits of practicing with old papers and how to approach them for maximum preparation.
Why Practicing with Past Papers Works

Working through previous tests offers several advantages:
- Familiarity with question patterns: By solving past problems, you become familiar with the types of questions asked and the structure of the test. This allows you to develop strategies to tackle each section more efficiently.
- Building confidence: Consistent practice builds confidence and reduces test anxiety. As you become more accustomed to solving questions within the time limit, you’ll feel more prepared when it’s time for the actual assessment.
- Identifying weak areas: Practicing old papers helps pinpoint areas where you may need additional review. If you consistently struggle with certain topics, you can focus your revision efforts on those areas.
How to Use Past Papers Effectively
Simply reviewing past papers isn’t enough; it’s important to approach them strategically:
- Simulate real test conditions: When practicing, try to replicate the test environment as closely as possible. Time yourself and avoid distractions, so you can gauge how well you manage time and handle pressure.
- Review your solutions: After completing a past paper, go through your solutions thoroughly. Analyze mistakes and learn from them. Make sure you understand why a particular approach didn’t work or where you could have improved.
- Work on one paper at a time: Focus on completing one full test before moving on to the next. This gives you a sense of progression and allows you to assess your improvement.
Table: Key Topics from Past Papers
Below is a table summarizing some common topics that appear in past tests. Use this as a guide to ensure you’re covering all essential areas.
| Topic | Frequency of Appearance |
|---|---|
| Limits and Continuity | High |
| Derivatives and Applications | Very High |
| Integrals and Antiderivatives | Moderate |
| Series and Sequences | High |
| Differential Equations | Moderate |
By practicing with past papers and using these strategies, you’ll not only familiarize yourself with the format of the test but also improve your problem-solving skills and increase your chances of success.
Resources for Further Calculus Study
To deepen your understanding of advanced mathematical concepts, it is important to explore various resources that enhance both theoretical knowledge and practical problem-solving skills. These materials provide different methods of learning, from comprehensive textbooks to interactive platforms, and will guide you in mastering the subject. Below are some of the most effective resources to continue your mathematical journey.
Books and Texts
Books remain a valuable source of structured content. They provide detailed explanations, step-by-step solutions, and practice exercises, making them an excellent option for self-study. Some key titles for further study include:
- “Advanced Calculus” by Lynn H. Loomis and Shlomo Sternberg: A rigorous and theoretical approach to higher-level mathematics.
- “Calculus: Early Transcendentals” by James Stewart: A comprehensive guide covering both concepts and applications of calculus.
- “Calculus” by Michael Spivak: A more challenging text, focusing on the theory and proofs behind calculus principles.
Online Platforms and Courses
Online platforms offer the flexibility to learn at your own pace, with interactive content and instant feedback. These resources cater to different learning styles and can be used alongside traditional study methods:
- Khan Academy: A popular platform offering free, interactive lessons and exercises that cover a wide range of mathematical topics.
- Coursera: Offers courses from top universities, often with video lectures, assignments, and peer interactions.
- MIT OpenCourseWare: Provides access to lecture notes, problem sets, and exams from MIT’s mathematics courses.
Interactive Tools
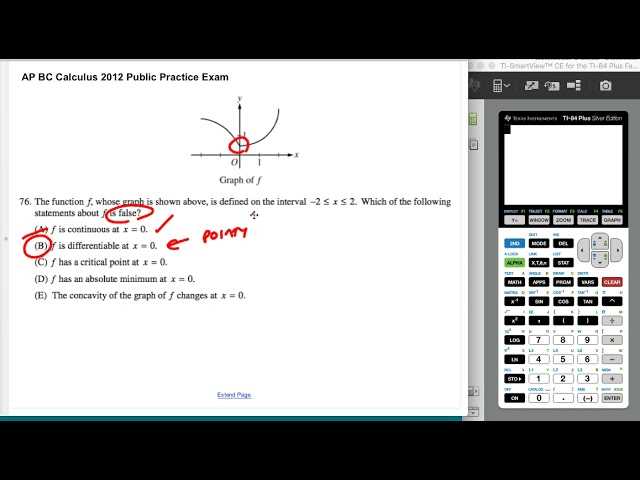
Using interactive tools can help visualize complex mathematical concepts and perform real-time calculations. These tools enhance understanding and provide an engaging way to practice:
- Desmos: A free graphing calculator that allows you to plot functions, explore derivatives, and visualize mathematical relationships.
- GeoGebra: A dynamic mathematics software that integrates geometry, algebra, calculus, and more.
- Wolfram Alpha: A powerful computational engine that provides detailed solutions and step-by-step explanations for various mathematical problems.
Table: Recommended Resources for Further Study
The table below summarizes some of the top resources that will help you advance your mathematical knowledge:
| Resource Type | Resource Name | Link |
|---|---|---|
| Textbook | “Advanced Calculus” by Lynn H. Loomis | Amazon Link |
| Online Course | Khan Academy | Khan Academy Link |
| Interactive Tool | Desmos | Desmos Link |
| Open Courseware | MIT OpenCourseWare | MIT OCW Link |
By utilizing these resources, you can strengthen your understanding of advanced mathematical topics, gain insight into complex concepts, and improve your problem-solving skills. Whether you prefer textbooks, online courses, or interactive tools, these materials will help you excel in your studies.
How the AP Calculus BC Assessment is Graded

The grading process for advanced mathematical assessments involves a combination of multiple-choice and free-response questions, which are designed to evaluate a student’s understanding of various topics. The scoring system takes into account both the accuracy of the responses and the method used to arrive at the solutions. Here is a breakdown of how this assessment is scored, helping students understand what is expected from them and how to maximize their performance.
Multiple-Choice Section

The multiple-choice section typically accounts for a significant portion of the total score. It is designed to assess a student’s knowledge of various concepts and their ability to apply them efficiently. Each correct answer contributes to the overall score, while incorrect or unanswered questions do not carry negative marks. The key points for this section include:
- Number of Questions: Usually 45 questions are asked in this section.
- Score Distribution: Each correct answer contributes a fixed number of points to the overall score.
- No Penalty for Incorrect Answers: Incorrect or skipped answers do not deduct points.
- Time Allocation: Students are allotted a set amount of time to answer these questions, requiring quick thinking and problem-solving ability.
Free-Response Section
The free-response section requires students to provide detailed solutions to a set of problems. Unlike the multiple-choice section, this part evaluates both the correctness of the answer and the reasoning behind it. Each question in this section is scored based on the following criteria:
- Accuracy: The answer must be correct, and any missteps in calculation or reasoning may result in losing points.
- Methodology: Points are awarded for showing the work and demonstrating a logical approach to solving the problem.
- Partial Credit: Even if the final answer is incorrect, partial credit is often awarded for correctly executed steps and valid reasoning.
- Time Management: Effective time management is crucial, as each problem requires a detailed solution, often involving multiple steps.
Scoring Scale and Final Results
The total score is determined by combining the results of both the multiple-choice and free-response sections. The final score is then converted into an overall numerical grade, which is often used to determine the level of understanding and mastery. Typically, the grading system includes:
- Total Possible Points: The total score ranges from 0 to 100, with both sections contributing to this total.
- Score Weighting: The multiple-choice section and the free-response section are weighted equally in determining the final score.
- Performance Levels: A student’s score is used to classify their performance into levels, often ranging from “not proficient” to “highly proficient.”
Understanding how the assessment is graded can help students focus their preparation efforts. By mastering both the accuracy and the methodology behind solving problems, students can maximize their performance and achieve a high score.