AP Statistics FRAPPY Answers Guide and Tips

Preparing for advanced exams in data analysis requires a strategic approach to problem-solving. It’s essential to understand the key concepts and how to apply them under timed conditions. This guide will help you navigate complex exercises commonly found in the test, offering insights into how to break down each question effectively and improve your performance.

Success in these exams isn’t just about memorizing formulas; it’s about developing a deep understanding of how to approach different types of problems. By honing your ability to analyze data sets, draw conclusions, and apply mathematical reasoning, you’ll be well-equipped to tackle any question that comes your way. Throughout this article, we’ll focus on techniques that can boost both your confidence and accuracy.

Problem-solving skills are critical for achieving high scores. Whether dealing with probabilities, distributions, or hypothesis testing, having a clear and structured method for solving challenges is key. By focusing on core principles and practicing consistently, you can significantly improve your results and feel more prepared for exam day.

Understanding AP Exam Problem Solving

To excel in advanced exam questions that assess data analysis skills, it’s essential to grasp the structure and types of problems presented. These challenges require a logical and methodical approach, where understanding the context and applying the right techniques can lead to successful solutions. Focusing on problem breakdown and clear interpretation is crucial for achieving accurate results.

Each problem generally involves multiple steps, from analyzing data sets to drawing meaningful conclusions. The goal is not only to compute numbers but also to demonstrate how well you understand the concepts and can apply them in real-world scenarios. Developing an organized approach allows you to solve complex exercises with confidence, focusing on accuracy and efficiency.

Approaching these exercises with a clear plan will help you identify relevant information, apply appropriate methods, and avoid common mistakes. By practicing regularly and familiarizing yourself with the types of problems you may encounter, you can improve both your speed and problem-solving ability during the exam.

What Are FRAPPY Questions in AP Exam

In the context of the AP exam, certain questions are designed to test your ability to apply theoretical knowledge to real-world situations. These problems require more than just basic calculations; they challenge your reasoning skills and ability to interpret data in meaningful ways. The goal is to assess your understanding of complex concepts and your ability to communicate your findings clearly.

Typically, these questions present a scenario involving a data set, from which you must derive conclusions. You’ll need to analyze the information, identify relevant patterns, and apply the appropriate techniques to solve the problem. These exercises are structured to mimic practical challenges, encouraging you to demonstrate both your analytical skills and your depth of understanding.

Key characteristics of these problems include multi-step reasoning, the use of graphs or tables, and the application of various methodologies such as hypothesis testing or probability calculation. Success in solving them relies not just on knowing the right formulas, but on effectively applying them in context, making these questions an important part of the exam.

How to Approach AP Exam Exercises

When tackling complex problems on the AP exam, it’s important to follow a systematic approach that allows you to break down each question into manageable steps. Start by reading the problem carefully and identifying key information, ensuring you fully understand the context before jumping into calculations. Rushing through a question can lead to misunderstandings, so take your time to analyze the data provided.

Next, decide on the appropriate methods or formulas to use. This step involves recalling relevant techniques that can be applied to the given data and ensuring that you are using them in the correct order. It’s essential to stay organized and structured in your approach to avoid missing any critical steps in the solution process.

Checking your work at the end is also crucial. Review your calculations and ensure that your conclusions align with the data presented. Make sure your answer is well-explained, showing both the method and the reasoning behind your solution. Practicing these steps regularly will improve both your confidence and performance when facing similar problems on the exam.

Key Strategies for Solving AP Exam Problems

When preparing for challenging problems on the AP exam, having a set of effective strategies is essential for success. These strategies not only help you approach each question logically but also ensure you can efficiently manage your time and avoid common mistakes. The key lies in having a structured method to follow and practicing consistently to build confidence.

Here are some strategies to keep in mind when solving complex questions:

Read the Problem Carefully: Always start by thoroughly understanding what the question is asking. Highlight important details and ensure you know what is required before starting your calculations.
Identify the Key Concepts: Determine which mathematical principles or methods apply to the question. This could include probability, hypothesis testing, or regression analysis, among others.
Break Down the Problem: Divide the problem into smaller, more manageable steps. Solving the problem in stages makes it easier to stay organized and ensure you’re not overlooking any critical parts.
Show All Work: Keep your calculations and thought process visible. This helps in verifying your solution later and also demonstrates a clear understanding of the problem-solving approach.
Check for Consistency: After solving, review the final answer to make sure it aligns with the given data and makes sense within the context of the problem.
Practice Regularly: The more problems you solve, the more familiar you become with the types of questions that may appear. Consistent practice helps reinforce the strategies and techniques you’ll need on exam day.

By applying these strategies, you can improve both your accuracy and efficiency when solving complex problems. Developing a systematic approach ensures you tackle each question with confidence and clarity, ultimately enhancing your performance on the exam.

Common Pitfalls in AP Exam Problems

When solving advanced exam problems, it’s easy to fall into traps that can lead to incorrect solutions. These pitfalls often arise from misinterpretations, rushing through calculations, or neglecting important steps in the process. Understanding the common mistakes and how to avoid them can make a significant difference in your overall performance.

Misreading the Question

One of the most frequent errors is failing to carefully read the problem. Often, students overlook crucial details or misunderstand what is being asked. It’s essential to pay attention to every part of the question, especially the wording, as it can significantly impact the approach and final solution.

Overlooking Assumptions and Conditions

Many questions involve assumptions or conditions that are vital for selecting the correct method. Ignoring these can lead to using inappropriate formulas or incorrect reasoning. Always double-check if the problem has any specific requirements, such as normality or independence, that could affect the calculations.

Common Mistake	How to Avoid It
Skipping steps in calculations	Write out each calculation fully to avoid missing critical details
Misapplying formulas	Ensure that the formula matches the problem’s context
Rushing through data interpretation	Take time to properly analyze data and identify relevant patterns
Ignoring units or rounding errors	Be mindful of units and rounding; check consistency throughout

Avoiding these pitfalls requires practice and careful attention to detail. By learning to recognize and address these common issues, you’ll improve both your accuracy and confidence when solving complex problems in the exam.

Essential Formulas for AP Exam Problem Solving

To successfully solve advanced problems on the AP exam, it’s crucial to have a solid grasp of key formulas and how to apply them. These formulas serve as the foundation for solving a wide range of exercises, from data analysis to probability calculations. Knowing when and how to use each formula can significantly speed up your problem-solving process and improve the accuracy of your results.

Below are some of the most important formulas that you should be familiar with, as they are commonly applied in various types of questions:

Formula	Application
Mean = (Σx) / n	Calculate the average of a data set
Variance = Σ(x – mean)² / (n – 1)	Measure the spread of data in a sample
Standard Deviation = √Variance	Determine the dispersion of data points
z = (x – μ) / σ	Standardize a value in a normal distribution
Confidence Interval = Mean ± (z* × SE)	Estimate a population parameter with a specified level of confidence
Regression Equation: y = mx + b	Model the relationship between two variables
P-value = P(Z > z)	Determine the probability of obtaining a result as extreme as the observed

By mastering these key formulas and understanding their applications, you’ll be able to tackle even the most complex problems on the exam with confidence and accuracy. Make sure to practice regularly, as familiarity with these formulas will improve both your speed and problem-solving ability during the test.

Breaking Down Probability AP Exam Questions

Probability problems on the AP exam can often seem complex at first glance, but with a structured approach, they become much more manageable. These questions typically require you to calculate the likelihood of certain events occurring based on a given scenario. To solve them effectively, it’s essential to understand key probability concepts and break down the problem step by step.

Start by clearly identifying the events in the problem. Make sure you understand what each variable represents and what is being asked. Then, determine the type of probability question you’re dealing with, whether it’s conditional probability, independent events, or the use of distributions. This will guide you in choosing the correct method and formula to apply.

Next, organize the information provided, such as sample space, outcomes, and probabilities. For example, if the problem involves a deck of cards or a set of dice, list the possible outcomes and calculate the respective probabilities. This makes it easier to visualize the problem and avoid common mistakes.

Key steps to follow:

Read the problem carefully and identify all events
Determine if events are independent or conditional
Choose the correct probability formula or method
Calculate individual probabilities and combine them as needed
Check for any additional conditions or constraints that might affect the answer

By breaking down probability problems into smaller components and following a logical process, you can avoid errors and confidently solve these questions on the exam.

Using Graphs in AP Exam Problem Solving

Graphs are powerful tools that help to visually represent data, making it easier to identify patterns, trends, and relationships. In AP exam problems, graphs play an essential role in providing insights that can guide your analysis and lead to more accurate solutions. By interpreting graphs correctly, you can gain a better understanding of the underlying concepts and apply the right methods to solve problems efficiently.

Types of Graphs You May Encounter

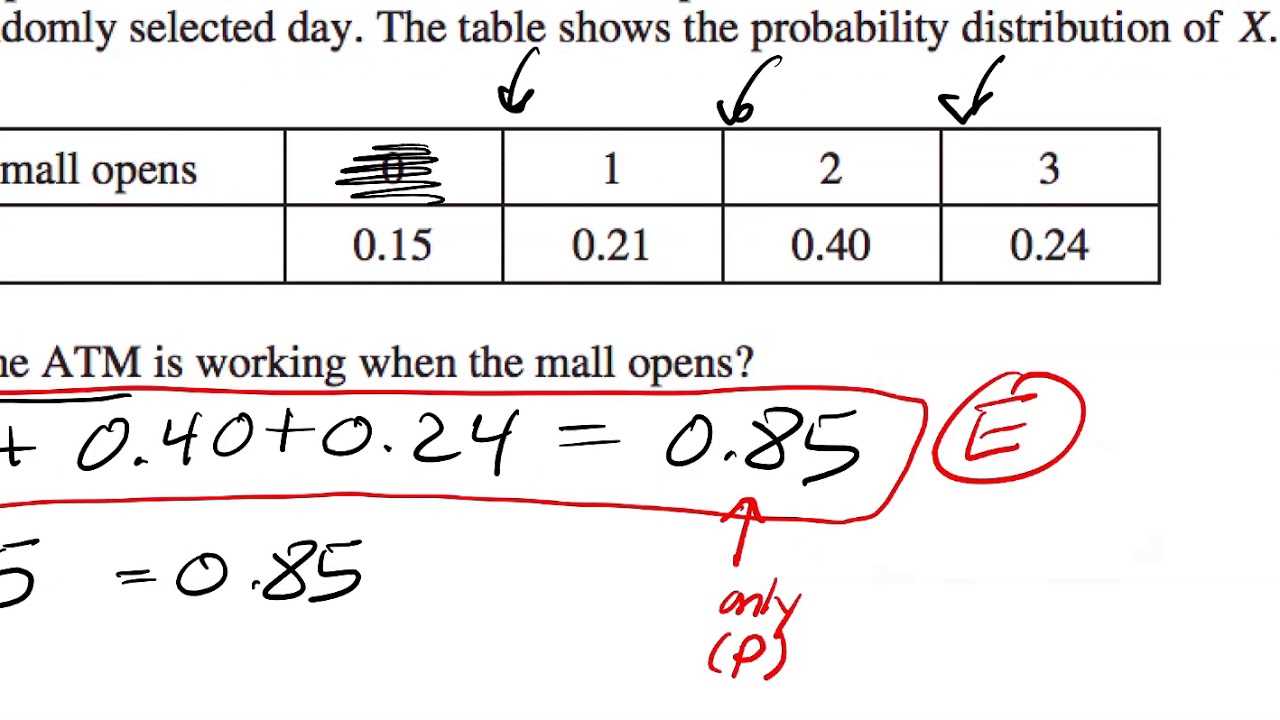
Different types of graphs are used to visualize various kinds of data. Knowing which graph to use and how to interpret it is crucial when approaching exam questions. Below are some common types of graphs you may encounter:

Bar Graphs: Used to represent categorical data and compare different categories.
Histograms: Display the distribution of continuous data, showing the frequency of values within certain ranges.
Scatter Plots: Show relationships between two variables, useful for identifying correlations.
Box Plots: Highlight the spread and central tendency of data, including the median, quartiles, and outliers.

Tips for Interpreting Graphs

When solving problems involving graphs, it’s essential to follow a clear process to extract useful information. Here are some tips:

Examine Axes: Check the axes labels and scales to understand what is being represented.
Identify Trends: Look for any trends or patterns in the data, such as linearity, clusters, or outliers.
Focus on Key Data Points: Pay attention to specific points that might answer the question or require further analysis.
Consider Relationships: If the graph shows two variables, look for any correlations or cause-and-effect patterns.

By effectively using graphs, you can simplify complex problems, avoid common mistakes, and make more informed decisions during the exam. Practice interpreting various types of graphs regularly to build confidence and improve your exam performance.

Tips for Time Management in AP Exam Problem Solving

Effective time management is crucial when tackling challenging problems during the AP exam. With a limited amount of time to answer each question, it’s essential to prioritize tasks, allocate time wisely, and stay focused. By following proven strategies, you can maximize your efficiency and ensure that you complete each section within the allotted time.

Prioritize Easy Questions First

Start by scanning the exam and identifying questions that you can solve quickly. These are often the ones that require basic calculations or straightforward logic. By tackling these questions first, you’ll build confidence and secure easy points, leaving more time for the more difficult problems.

Break Complex Problems into Steps

For more complicated questions, take the time to break them down into smaller, manageable steps. Focus on understanding the key components of the problem and how they relate to one another. This approach will help you avoid feeling overwhelmed and ensure that you address each part of the problem systematically.

Estimate Time for Each Section: Allocate a specific amount of time to each question or section. If a problem is taking too long, move on to the next one and return to it later.
Stay Calm and Focused: Time pressure can cause stress, but maintaining focus and staying calm will help you think clearly and work more efficiently.
Avoid Overthinking: Don’t dwell too long on any one question. Trust your instincts and move on if you find yourself stuck.

By using these time management techniques, you can maximize your performance on the exam, ensuring that you complete all questions within the time limit without sacrificing accuracy. Practice these strategies during mock exams to develop a rhythm and boost your confidence on the actual test day.

How to Interpret Statistical Data Correctly

Interpreting data accurately is essential for solving complex problems and making informed decisions. In many cases, raw numbers and figures can be misleading if they are not properly understood. It’s important to not only analyze the data itself but also to consider the context in which it was collected, as well as the methods used to obtain it. Proper interpretation ensures that you draw meaningful conclusions and avoid common pitfalls in your reasoning.

The first step in interpreting data is to understand the type of data you’re working with–whether it’s categorical or continuous–and how it has been organized. This will determine which methods of analysis are appropriate. For example, while measures like mean and median are useful for continuous data, frequency tables and percentages are more suited to categorical data.

Another critical aspect of interpretation is recognizing the potential biases or limitations of the data. Check for any external factors that might affect the results, such as sample size, sampling method, or potential confounding variables. Being aware of these factors helps to contextualize your findings and avoid drawing inaccurate conclusions.

Examine the Source: Ensure the data comes from a reliable and unbiased source to maintain its credibility.
Check for Outliers: Identify any values that fall outside the normal range, as they could skew your analysis.
Consider the Distribution: Understand the spread and central tendency of the data to gain insights into its overall pattern.
Look for Correlations: Be cautious when interpreting relationships between variables–correlation does not imply causation.

By carefully analyzing data and considering all relevant factors, you can interpret information more accurately and use it to make sound decisions. Developing a thorough understanding of data interpretation techniques will also help you solve problems more effectively in exams and real-world situations.

Working with Hypothesis Testing in AP Problem Solving

Hypothesis testing is a critical method used to make decisions or inferences about a population based on sample data. It involves proposing an assumption or hypothesis about a parameter and then determining whether the sample data supports or contradicts that assumption. In the context of problem-solving, it is essential to apply this process systematically to draw valid conclusions and make reasoned decisions based on the available evidence.

Steps for Conducting a Hypothesis Test

When working with hypothesis tests, it’s important to follow a structured approach to ensure accurate results. The process typically involves several key steps:

State the Hypotheses: Begin by clearly defining the null hypothesis (H₀) and the alternative hypothesis (H₁). The null hypothesis represents the assumption that there is no effect or difference, while the alternative hypothesis suggests the opposite.
Choose the Significance Level: Select an appropriate significance level (α), which determines the threshold for rejecting the null hypothesis. A common value is 0.05, meaning there is a 5% chance of making an incorrect decision.
Collect and Analyze Data: Gather your sample data and perform the necessary calculations, such as calculating the test statistic and the corresponding p-value.
Make a Decision: Compare the p-value to the significance level. If the p-value is less than α, reject the null hypothesis. Otherwise, fail to reject the null hypothesis.

Common Mistakes to Avoid

While hypothesis testing is a powerful tool, it is easy to make mistakes if the process is not followed carefully. Here are some common pitfalls to watch out for:

Misinterpreting the p-value: A p-value is not the probability that the null hypothesis is true. It simply indicates the strength of the evidence against it.
Not Considering Effect Size: Even if a hypothesis test is statistically significant, it’s important to evaluate the practical significance of the result.
Ignoring Assumptions: Many tests rely on certain assumptions, such as normality of the data. Failing to check these assumptions can lead to inaccurate conclusions.

By following these steps and avoiding common errors, you can effectively apply hypothesis testing to solve complex problems and draw valid conclusions based on sample data. Practicing these techniques will improve your problem-solving skills and increase your confidence in hypothesis-driven analysis.

Dealing with Regression in AP Problem Solving

Regression analysis is a powerful technique used to examine the relationship between two or more variables. It helps to understand how one variable influences another, making it essential in many problem-solving scenarios. When working with regression, it is important to focus on identifying the best-fitting model for the data and understanding the relationship it represents. Whether you’re dealing with simple linear regression or more complex models, knowing how to interpret the results correctly is key to drawing meaningful conclusions.

Key Concepts in Regression Analysis

To apply regression analysis effectively, you need to understand the key concepts involved. These include:

Dependent and Independent Variables: The dependent variable is the one you’re trying to predict or explain, while the independent variable(s) are the predictors or factors that influence the dependent variable.
Regression Line: This is the line that best fits the data points in a linear regression model. It represents the relationship between the variables and is used to make predictions.
R-squared Value: The R-squared value indicates the proportion of variance in the dependent variable that can be explained by the independent variable(s). A higher R-squared suggests a stronger relationship.
Residuals: Residuals are the differences between the observed and predicted values. Analyzing residuals can help determine the quality of the regression model.

Interpreting Regression Results

Once you’ve performed regression analysis, interpreting the results accurately is crucial. Below is a summary of key points to consider:

Metric	Meaning
Intercept	The value of the dependent variable when all independent variables are zero.
Slope	Indicates the change in the dependent variable for each unit increase in the independent variable.
p-value	Helps determine whether the relationship between variables is statistically significant. A small p-value (typically
R-squared	Measures the proportion of variance in the dependent variable that can be explained by the independent variables.

By understanding and applying these concepts, you can effectively deal with regression problems in AP problem-solving scenarios. Regression analysis allows you to model relationships, make predictions, and assess the strength of those predictions, which are essential skills in both academic and real-world applications.

AP Stats: Confidence Intervals Explained

Confidence intervals are a fundamental concept in data analysis, providing a range of values within which we can reasonably expect a population parameter to lie. These intervals are used to quantify the uncertainty around a sample estimate and allow researchers to make inferences about larger populations. Understanding how to calculate and interpret confidence intervals is critical for drawing valid conclusions based on data.

The confidence interval is typically expressed with a specified level of confidence, such as 95% or 99%. This percentage indicates how confident we are that the interval contains the true population parameter. For example, a 95% confidence interval means that if we were to repeat the sampling process multiple times, 95% of the calculated intervals would contain the true parameter value.

Key Components of a Confidence Interval:

Point Estimate: This is the initial estimate of the population parameter based on the sample data, such as the sample mean or proportion.
Margin of Error: This represents the amount of variability in the estimate, usually based on sample size and variability within the data. It helps define the range of the confidence interval.
Confidence Level: The chosen level of confidence, such as 95% or 99%, indicates the probability that the interval contains the true parameter value.

Calculating a Confidence Interval:

The general formula for a confidence interval for a population mean is:

Confidence Interval = Point Estimate ± (Critical Value × Standard Error)

Here, the point estimate is typically the sample mean, the critical value is derived from the chosen confidence level, and the standard error is a measure of the variability in the sample data.

Interpreting Confidence Intervals:

When interpreting a confidence interval, remember that the interval provides a range of plausible values, but it does not guarantee that the true population parameter lies within that range for any single sample. The higher the confidence level, the wider the interval will be, reflecting greater uncertainty about the exact value of the parameter.

In practice, confidence intervals are widely used in hypothesis testing, estimation, and decision-making processes. A correctly interpreted confidence interval allows for better-informed conclusions while acknowledging the inherent uncertainty in sampling and data collection.

Making Use of Descriptive Analysis

Descriptive methods provide a way to summarize and describe the essential features of a data set. By using various techniques to present data in a manageable form, we can better understand the main characteristics, patterns, and relationships within the data. This approach plays a key role in providing an overview of the data, helping to identify trends, compare groups, and inform decisions.

Typically, descriptive methods involve the use of central tendency measures, variability measures, and visual representations. These tools help simplify large datasets, making them easier to interpret and analyze. They are often the first step before performing more complex analyses or drawing conclusions from the data.

Key Measures in Descriptive Analysis

Mean: The average value of a set of numbers, giving an overall sense of the “central” value.
Median: The middle value that divides the data into two equal halves, providing a measure of central location less affected by outliers.
Mode: The most frequent value in the dataset, useful for identifying common trends.
Range: The difference between the highest and lowest values, showing the extent of variation within the dataset.

Visualizing Data

In addition to numerical measures, graphical representations are essential in simplifying data interpretation. Common visual tools include:

Histograms: Used to show the distribution of numerical data and identify patterns or outliers.
Boxplots: Help to visualize the spread and central tendency of data, highlighting the interquartile range and potential outliers.
Bar Charts: Effective for comparing different categories or groups within the data.

By combining these numerical and visual techniques, you can gain a clearer understanding of the data at hand. Descriptive analysis not only simplifies complex information but also serves as a foundation for more advanced analytical methods.

Advanced Techniques for FRAPPY Solutions

In tackling complex problems, mastering advanced techniques is essential for achieving accurate and efficient solutions. These strategies build on foundational methods, allowing you to address more intricate questions with a higher level of precision. Understanding how to apply these methods effectively is crucial for overcoming challenges that require deeper analysis and interpretation of data.

Advanced approaches often involve a combination of different methods, each providing insights from a unique perspective. Whether it’s through leveraging more sophisticated models or utilizing multi-step reasoning, these techniques enable a more thorough exploration of the data and its underlying patterns.

Key Techniques to Enhance Problem Solving

Multiple Regression Analysis: Used to explore the relationship between several variables, helping to predict outcomes based on multiple factors.
Bayesian Inference: A powerful statistical method for updating the probability of a hypothesis based on new evidence, ideal for dynamic situations.
Simulations: Running repeated trials to model complex systems and understand the behavior of a system under various conditions.
Bootstrap Methods: A resampling technique that helps estimate the distribution of a statistic by repeatedly sampling with replacement.

Leveraging Advanced Visual Tools

In addition to analytical methods, advanced visual tools can offer significant insight into the data, allowing for clearer interpretation of results. Some examples include:

Heatmaps: Visualizing correlations between variables, particularly useful for understanding large, complex datasets.
Time Series Plots: Ideal for examining data over time and identifying trends or cyclical patterns.
Pair Plots: Used to visualize relationships between multiple variables and uncover potential interactions.

By incorporating these advanced techniques into your problem-solving toolkit, you can approach even the most challenging tasks with greater confidence and accuracy, ultimately leading to more robust conclusions and decisions.

Improving Accuracy in AP Stats FRAPPY

Achieving precise results in complex problems requires attention to detail and a strategic approach to data analysis. Whether you’re working with numerical models or interpreting graphical representations, the goal is to enhance accuracy through thoughtful methods and careful execution. Accuracy not only improves the quality of your conclusions but also strengthens your ability to solve even the most intricate tasks.

To refine your accuracy, it’s essential to approach each problem systematically. Identifying key variables, eliminating potential sources of error, and employing effective strategies are all crucial steps in ensuring your solutions are both precise and reliable.

Strategies for Enhancing Precision

Double-Check Your Calculations: Small errors can lead to large discrepancies. Always verify each step of your work to ensure accuracy in your computations.
Use Appropriate Models: Selecting the right model or approach for the problem at hand can significantly increase the reliability of your results.
Be Mindful of Assumptions: Clearly understand the assumptions behind any model or method you use, as incorrect assumptions can skew the outcome.
Refine Your Data Interpretation: Avoid overgeneralizing or misinterpreting the data. Pay close attention to the context and the relationships between variables.

Utilizing Tools for Greater Accuracy

To further improve the accuracy of your solutions, there are several tools and techniques that can assist in both computation and analysis:

Graphing Calculators: These tools can help verify results and perform complex calculations more accurately than manual methods.
Software for Data Visualization: Tools like Excel or R allow for precise plotting and can help you identify trends or patterns that might be missed with raw data.
Statistical Tables: Relying on trusted statistical tables for reference can minimize errors in critical areas like probability calculations.

By adopting these practices and leveraging the right tools, you can significantly enhance the accuracy of your work, leading to more reliable conclusions and a deeper understanding of the problems you’re solving.

Reviewing FRAPPY Answers for Mistakes

When tackling complex problems, the review process is just as important as the initial attempt. Carefully going over your work allows you to catch errors, refine your reasoning, and ensure that all aspects of the problem have been properly addressed. A mistake, no matter how small, can lead to incorrect conclusions, so taking time to double-check your work is an essential step toward improving your problem-solving skills.

The process of reviewing answers for mistakes involves several key steps. Start by revisiting the question itself, ensuring that you’ve understood every part of it. Then, go through each step of your solution to identify any potential miscalculations, overlooked assumptions, or logical gaps. It’s crucial to be methodical in this process to avoid skipping over any possible errors.

Key Steps in the Review Process

Recheck Your Assumptions: Ensure that the assumptions you made at the start are valid and don’t skew your results.
Verify Mathematical Calculations: Go over each calculation step carefully. Even small arithmetic errors can have a big impact on the final result.
Ensure Proper Interpretation: Double-check that you’re interpreting the problem correctly, especially when working with complex data sets or graphs.
Look for Overgeneralizations: Be mindful of drawing conclusions too quickly, especially when the data or the conditions are nuanced.

In addition to self-review, it can be beneficial to have someone else check your work. A fresh perspective may reveal mistakes you’ve missed or provide valuable feedback on your approach.

By incorporating a detailed and systematic review process, you can ensure that your answers are accurate, reliable, and logically sound. Taking the time to identify and correct mistakes will not only help improve the quality of your work but also build confidence in your problem-solving abilities.