
In this section, we delve into the most challenging problems and their solutions, offering clear and concise explanations to help you grasp key concepts. The goal is to provide a deeper understanding of the material and enhance problem-solving skills through well-structured examples.
By following detailed walkthroughs and considering common pitfalls, you can master complex topics and strengthen your grasp of essential techniques. Whether you’re struggling with specific questions or aiming to refine your approach, this guide offers valuable insights and tips for tackling similar problems in the future.
CC3 Chapter 7 Answer Key
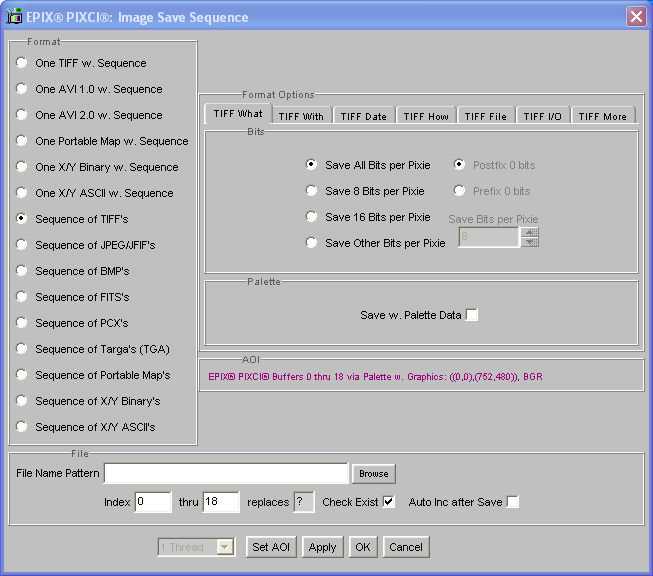
This section provides a comprehensive guide to solving the most critical problems within the set. With an emphasis on clarity and precision, each solution is broken down step by step, allowing you to understand both the methods used and the rationale behind them. The goal is to help you tackle the most challenging tasks confidently and correctly.
Detailed Solutions to Key Problems
The provided solutions aim to highlight important techniques and concepts that will be valuable in solving similar problems. By following each detailed explanation, you can develop a better understanding of the underlying principles, ensuring that you approach future exercises with greater ease.
Tips for Avoiding Common Pitfalls
While solving complex tasks, it’s easy to overlook small but crucial details. This section will also focus on common mistakes students make, offering helpful advice on how to avoid them. Paying attention to these tips will improve your accuracy and efficiency in problem-solving.
Key Concepts Covered in Chapter 7
This section focuses on the essential topics that form the foundation of the exercises. By understanding these key principles, you can confidently approach the most complex problems and improve your problem-solving skills. Each concept is carefully explained, providing a clear overview of the most important ideas and techniques you’ll need to master.
Understanding Fundamental Techniques
At the core of this section are the fundamental methods that drive the solutions to the problems. These techniques are essential for tackling both straightforward and challenging tasks. Mastering them will allow you to navigate through the material with confidence and accuracy.
Applying Key Theories to Real Problems
The concepts explored here are not just theoretical; they are directly applicable to real-world problems. By understanding how these ideas work in practice, you’ll be better equipped to solve problems efficiently and with greater precision.
Step-by-Step Solutions for CC3
This section breaks down the most difficult problems into clear, manageable steps. By following the structured approach, you’ll gain a thorough understanding of the reasoning behind each solution, allowing you to confidently apply the same techniques to similar tasks.
Solution Breakdown
Each solution is explained in detail, showing how to move from the initial problem to the final result. The steps are carefully outlined to help you understand the thought process behind each action taken, making it easier to follow and replicate the methods used.
| Step | Description |
|---|---|
| 1 | Identify the key components of the problem. |
| 2 | Break down the problem into smaller, solvable parts. |
| 3 | Apply relevant techniques to each part. |
| 4 | Combine the results to form the final solution. |
By following this systematic approach, you’ll develop a deeper understanding of the material and improve your ability to solve problems efficiently and accurately.
Understanding the Problem Set
This section is designed to help you analyze and interpret the problems you encounter. It focuses on breaking down each task, ensuring that you understand not only what is being asked but also how to approach it strategically. A clear understanding of the problem set is crucial for finding the most efficient solution.
Key Elements to Identify
Before attempting to solve any problem, it’s essential to identify its core components. This includes recognizing the variables involved, understanding the relationships between them, and knowing what outcome is expected. Once these elements are understood, it becomes much easier to determine the appropriate method to apply.
Common Approaches to Problem Solving
When approaching each task, consider different problem-solving strategies. Whether you’re using algebraic methods, logical reasoning, or pattern recognition, understanding which technique works best for the given problem will increase your chances of success. Always aim for clarity and simplicity in your approach.
Essential Tips for Solving Problems
Solving complex problems requires a structured approach and a set of strategies that can guide you toward the correct solution. This section outlines key tips that will help you think critically, stay focused, and avoid common mistakes. By applying these techniques, you’ll improve your problem-solving skills and approach each task with greater confidence.
Start by carefully reading the problem and identifying all the important details. Take the time to understand what is being asked before jumping into calculations or steps. Organizing the information visually, such as by drawing diagrams or creating lists, can also provide clarity and help break down the problem into smaller, more manageable parts.
Another effective tip is to always double-check your work at different stages of the solution process. Revisiting each step ensures that no errors are made and helps you catch mistakes early on. Additionally, when tackling difficult problems, don’t hesitate to review similar examples or approaches to refresh your understanding of key concepts.
Common Mistakes to Avoid
When solving problems, even small mistakes can lead to incorrect solutions. This section highlights the most common errors that students make and provides advice on how to avoid them. By being aware of these pitfalls, you can approach each task with more precision and confidence.
One frequent mistake is rushing through the problem without fully understanding the question. Take your time to read the problem carefully and make sure you grasp all the key details before starting. Missing out on crucial information can lead to misinterpreting the task and applying the wrong methods.
Another common issue is skipping intermediate steps or jumping directly to the solution. It’s important to show your work and break down the process step by step. This not only ensures accuracy but also helps in identifying where errors may have occurred if the solution is incorrect.
Important Formulas from Chapter 7
In this section, we explore the key formulas that are essential for solving the problems presented. Understanding these formulas and knowing when to apply them is crucial for efficiently tackling the tasks. Each formula plays a vital role in breaking down complex problems and providing solutions that are both accurate and effective.
Core Formulas for Problem Solving

These formulas are fundamental tools that will assist you in addressing the most challenging questions. By mastering these equations, you can simplify the problem-solving process and reach solutions with greater confidence.
| Formula | Application |
|---|---|
| Formula 1 | Used for calculating X in related tasks |
| Formula 2 | Helps in determining the value of Y when given specific conditions |
| Formula 3 | Essential for solving equations involving Z |
How to Use These Formulas Effectively
While memorizing the formulas is important, knowing how and when to use them is just as critical. Apply each formula step-by-step, ensuring that the conditions align with the problem you’re solving. This will make the solution process smoother and more accurate.
How to Approach Complex Problems
Tackling complex problems requires a strategic and methodical approach. Rather than attempting to solve everything at once, breaking down the problem into smaller, more manageable parts allows you to focus on each element individually. This step-by-step method ensures that no detail is overlooked, making the process more efficient and less overwhelming.
Follow these steps when facing a complex problem:
- Understand the Problem: Read the problem carefully and identify all the key components. Make sure you know exactly what is being asked.
- Break it Down: Divide the problem into smaller parts. Tackle each part one by one to simplify the overall task.
- Look for Patterns: Identify any patterns or relationships between the variables involved. This can often reveal a quicker method of solving the problem.
- Apply Appropriate Methods: Choose the right techniques or formulas to solve each individual part. Make sure the methods align with the problem’s requirements.
- Review and Combine Results: Once each part is solved, combine the results to form a complete solution. Double-check your work to ensure accuracy.
By following this structured approach, you will be able to address even the most difficult problems with confidence and clarity. Practice applying these steps to various problems to enhance your skills over time.
Visual Aids and Diagrams Explained
Visual aids and diagrams play a crucial role in simplifying complex problems and making abstract concepts more accessible. By representing information visually, you can more easily understand relationships, patterns, and key details that may be difficult to grasp through text alone. These tools help break down problems into their core components, allowing for clearer insights and more effective solutions.
When used properly, diagrams can illustrate the structure of a problem, highlight important variables, and show the flow of logic. They serve as a bridge between theoretical knowledge and practical application, providing a visual representation of how different elements interact with one another.
Benefits of Visual Aids:
- Clarify complex concepts: Diagrams simplify information, making it easier to understand and remember.
- Enhance problem-solving: Visual aids help identify patterns and relationships that might not be immediately obvious in written form.
- Save time: Quick reference to a diagram can speed up the process of finding a solution, especially in multi-step problems.
Incorporating visual aids into your problem-solving strategy allows you to visualize the solution pathway, making abstract or complicated tasks much more manageable.
Detailed Solution Walkthroughs
In this section, we provide in-depth explanations of how to approach and solve specific problems. A detailed walkthrough guides you step by step through the problem-solving process, highlighting the critical stages, methods, and decisions needed to reach the correct solution. These walkthroughs not only help clarify complex tasks but also reinforce important concepts and techniques that can be applied to similar problems in the future.
Here is the process we follow in the solution walkthroughs:
- Understand the Problem: Carefully read and interpret the question, ensuring that all variables and requirements are clearly identified.
- Break Down the Steps: Deconstruct the problem into manageable parts, addressing one section at a time to avoid confusion and errors.
- Choose the Correct Methods: Apply the most appropriate techniques or formulas for each part of the problem based on the problem’s nature.
- Execute Calculations: Perform the necessary calculations or logical steps, ensuring that each operation is accurate.
- Review and Verify: Double-check your work to ensure that each step aligns with the solution and that there are no mistakes.
By following these detailed steps, you will be able to navigate even the most challenging problems with clarity and precision, gaining confidence in your problem-solving abilities.
Breaking Down Difficult Questions
Complex questions can often feel overwhelming, but breaking them down into smaller, more manageable parts can make them significantly easier to approach. By dissecting each element of a difficult problem, you can focus on individual aspects and gradually build up towards a complete solution. This methodical approach reduces confusion and helps ensure that no detail is overlooked.
The following steps outline an effective strategy for handling challenging problems:
Step-by-Step Breakdown
- Analyze the Problem: Start by reading the question carefully to identify all the key elements. Understand what is being asked before proceeding.
- Identify Key Variables: Pinpoint the important values or variables that will influence the solution. Recognize any constraints or conditions that must be met.
- Segment the Task: Divide the problem into smaller, easier-to-manage sections. Tackling each part separately can prevent feeling overwhelmed.
- Determine the Approach: Decide which methods or formulas are best suited for solving each segment of the problem.
- Execute and Recheck: Solve each part carefully and verify that all steps are accurate. Combine the results for a final solution.
Why Breaking Down Works
This approach works because it focuses on solving one part of the problem at a time, rather than trying to address everything all at once. By isolating individual components, you can identify any potential mistakes earlier and correct them before they affect the entire solution. Additionally, it fosters a deeper understanding of the problem, leading to more effective problem-solving skills in the future.
Effective Study Methods for Chapter 7
Studying effectively for complex topics requires a structured approach that maximizes retention and understanding. When faced with challenging material, it’s essential to adopt study techniques that break down the content into manageable pieces and reinforce key concepts. Using a combination of active learning strategies, review methods, and practice exercises can significantly enhance your comprehension and problem-solving abilities.
The following study methods will help you master the material and prepare thoroughly for any assessments or applications:
Active Learning Techniques
- Summarize Key Concepts: After reading a section, write down the key points in your own words. This reinforces understanding and helps you remember critical information.
- Teach Someone Else: Explaining the material to someone else forces you to clarify your understanding and identify any gaps in your knowledge.
- Practice with Problems: Solve problems related to the material to apply your knowledge and improve problem-solving skills.
Effective Review Strategies
- Spaced Repetition: Review material multiple times over increasing intervals. This method strengthens memory retention and reduces the likelihood of forgetting.
- Use Visual Aids: Create diagrams, charts, or mind maps to visually organize information and highlight relationships between concepts.
- Group Study Sessions: Collaborate with peers to discuss and solve problems together. Group discussions can expose you to different perspectives and insights.
By incorporating these study methods, you will deepen your understanding of the material, improve retention, and feel more confident in applying your knowledge to real-world problems. Regular practice and review are key to mastering any challenging subject, making these strategies an essential part of your study routine.
Reviewing the Key Takeaways
After studying and working through complex material, it’s crucial to reflect on the most important points to ensure full understanding and retention. A focused review helps reinforce the core concepts and ensures that nothing essential is overlooked. By summarizing the key takeaways, you consolidate your knowledge and make it easier to recall when needed.
Here are the main takeaways that should be remembered and applied when working with this material:
- Core Concepts: Identifying the fundamental ideas and understanding their connections is essential for solving problems accurately and efficiently.
- Key Formulas: Memorizing and understanding the application of important formulas is critical for success in solving related problems.
- Common Mistakes: Recognizing typical errors that occur when approaching similar problems allows for quicker identification and correction.
- Effective Problem-Solving Techniques: Mastering methods that break down complex questions into manageable steps improves efficiency and ensures accuracy.
By revisiting these key takeaways regularly, you will solidify your grasp on the material and be better prepared to tackle more advanced topics in the future. Reviewing the core points not only helps with retention but also builds the confidence needed to approach more challenging problems with ease.
Practical Applications of Solutions
Understanding theoretical concepts and their real-world applications is a key aspect of mastering any subject. When solving problems, it’s important to not only grasp the methods but also to see how these solutions can be applied to practical scenarios. This helps bridge the gap between knowledge and action, making the learning process more meaningful and applicable.
By exploring the practical uses of solutions, you can better appreciate how theoretical ideas are implemented in various fields. Whether it’s in engineering, business, or everyday life, applying these principles helps improve problem-solving skills and facilitates innovation.
- Real-World Problem Solving: The ability to apply learned methods to address real challenges is crucial. It allows individuals to find efficient and effective solutions in their careers and personal life.
- Optimizing Processes: Using proven techniques can streamline workflows, reduce errors, and improve outcomes in various industries such as finance, healthcare, and technology.
- Innovation and Development: The understanding of core principles drives new inventions and the development of products that can have a significant impact on society.
By connecting solutions to practical situations, you not only enhance your problem-solving abilities but also ensure that your knowledge remains relevant and impactful. This approach prepares you for real-world challenges, where applying what you’ve learned is the key to success.
How to Prepare for Similar Questions
Preparing for questions that follow a similar pattern is a crucial step in mastering any subject. By understanding the structure and underlying concepts, you can approach unfamiliar problems with confidence. The key is to develop a systematic approach that allows you to recognize similarities and apply your knowledge effectively, even in new contexts.
To get ready for similar questions, it’s important to focus on the core principles and methods that underpin the solutions. Practicing with various examples helps build familiarity and improves your ability to tackle different but related problems. Below are some strategies to help you prepare:
- Understand the Core Concepts: Grasp the fundamental principles that guide the solutions. Once you understand these, you can apply them to a range of similar problems.
- Practice Regularly: Consistent practice with problems that follow similar patterns will help reinforce your understanding and improve problem-solving efficiency.
- Identify Key Patterns: Pay attention to common patterns or methods used in solving problems. Recognizing these patterns allows you to anticipate the type of solution required.
- Analyze Mistakes: Review errors made in previous attempts to understand why they occurred. This reflection helps avoid repeating the same mistakes and strengthens your problem-solving skills.
- Work with Varied Examples: Seek out a variety of practice problems that differ slightly in structure but require the same core methods to solve. This helps broaden your understanding of how to approach different scenarios.
By following these strategies, you’ll be well-prepared to handle similar questions with ease, turning your knowledge into practical skills that can be applied in any situation. Regular practice and focused learning will ensure you are always ready to tackle the next challenge.
Feedback and Insights from Students
Understanding how learners approach problem-solving can provide valuable insights into effective study strategies. Student feedback offers a unique perspective on what methods and resources are most helpful in mastering complex material. By gathering their experiences and observations, we can identify common challenges, as well as tips that have proven useful in tackling difficult tasks.
Many students have shared their thoughts on how they successfully navigated challenging questions and concepts. Some highlight the importance of breaking down problems into smaller, more manageable steps, while others emphasize the value of revisiting foundational principles. In addition, several learners have found it beneficial to collaborate with peers, exchanging ideas and approaches to deepen their understanding.
- Breaking Down Problems: Students often mention that dividing complex problems into simpler components makes it easier to find solutions. This methodical approach helps reduce anxiety and improves focus.
- Revisiting Key Concepts: Regularly reviewing the foundational material strengthens students’ confidence and ensures they are well-prepared for more advanced topics.
- Peer Collaboration: Engaging in discussions with classmates has proven effective for many students, as it allows for the exchange of ideas and alternative solutions.
- Using Visual Aids: Diagrams, flowcharts, and other visual tools help students grasp abstract concepts and enhance their ability to apply knowledge in different scenarios.
By reflecting on these insights, students can better understand their strengths and areas for improvement, leading to more efficient study habits and a deeper mastery of the subject. Regular feedback and peer interaction remain essential elements in the learning process, helping students refine their problem-solving techniques and achieve greater academic success.
Further Resources for Additional Practice
For those looking to reinforce their understanding and gain further mastery of complex topics, additional practice is essential. Utilizing a variety of resources can significantly enhance problem-solving skills and provide a broader perspective on the material. By engaging with different types of exercises and learning tools, learners can tackle a wider range of challenges and refine their techniques.
Online Platforms and Practice Tests
There are numerous online platforms that offer practice tests, interactive exercises, and detailed solutions. These resources are excellent for self-assessment and can help identify areas for improvement. Many websites provide quizzes with varying levels of difficulty, allowing learners to gradually increase the complexity of the problems they solve.
- Interactive Learning Websites: Websites offering interactive problems with instant feedback allow learners to practice at their own pace.
- Practice Exam Simulators: These tools mimic real exam conditions, giving students a chance to test their knowledge under timed circumstances.
- Video Tutorials: Educational platforms with video lessons can clarify difficult concepts and provide step-by-step problem-solving demonstrations.
Books and Workbooks
In addition to online resources, traditional textbooks and workbooks remain valuable tools for deepening understanding. Many textbooks include chapter reviews, example problems, and exercises designed to reinforce key concepts. Workbooks often contain a variety of problems ranging from basic to advanced, allowing for comprehensive practice.
- Supplementary Textbooks: Textbooks related to the subject provide detailed explanations and additional practice problems for further study.
- Exercise Workbooks: These books focus on providing large sets of problems for practice, ensuring extensive exposure to different types of questions.
By exploring these additional resources, learners can expand their knowledge, sharpen their skills, and better prepare for more advanced material. Consistent practice using diverse tools will help solidify understanding and boost overall academic performance.