
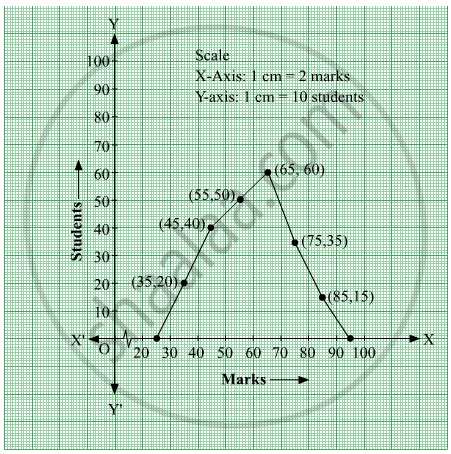
In this section, we will explore fundamental techniques and methods that are crucial for analyzing and interpreting numerical data. By focusing on key problem-solving strategies, we aim to provide clear insights into how data sets can be understood and manipulated effectively.
Whether you’re dealing with averages, distributions, or various forms of analysis, it is essential to have a firm grasp on the basic tools that help in making sense of raw data. This section offers a step-by-step approach to mastering essential skills and gaining clarity in tackling complex problems.
From descriptive summaries to more advanced methods of evaluation, this guide is designed to break down the most important topics, providing practical examples and solutions. By the end of this section, you’ll be equipped with the knowledge to confidently approach and solve related tasks with ease.
Chapter 6 Answer Guide
This section provides a comprehensive guide to the essential concepts and methods needed to tackle the challenges found in the sixth part of the course. It focuses on key approaches that help break down complex tasks and offers step-by-step solutions to common problems. Mastering these techniques will enhance your understanding and ability to analyze various sets of data efficiently.
Understanding Core Techniques
Each topic in this section builds upon fundamental principles that are crucial for any form of data analysis. Whether you are calculating averages, measuring variability, or exploring relationships within data, the guide offers detailed instructions to ensure clear comprehension. By following these steps, you will be able to approach each problem systematically, ensuring accuracy and clarity in your results.
Practical Examples and Applications

Real-life scenarios are included to help you apply what you’ve learned. These examples demonstrate how to use the core methods effectively in practical situations. The solutions provided not only clarify the steps involved but also highlight common mistakes to avoid, ensuring that you can work through similar problems on your own in the future.
Overview of Key Concepts in Data Analysis
This section explores the essential techniques and principles that form the foundation of effective data interpretation and problem-solving. Understanding these core ideas is crucial for analyzing and drawing meaningful conclusions from numerical data. Whether you are working with central tendencies or evaluating data spread, mastering these concepts ensures accurate results in every analysis.
Important Methods to Master
To analyze data effectively, it is necessary to understand various methods such as identifying averages, measuring variability, and examining data distribution. These tools are widely used across different scenarios to simplify complex information and help make informed decisions. Below is an overview of the most common methods:
| Method | Description |
|---|---|
| Mean | The average value of a data set, calculated by summing all values and dividing by the number of values. |
| Median | The middle value in a sorted data set, useful when data is skewed. |
| Mode | The most frequently occurring value in a data set. |
| Range | The difference between the highest and lowest values in a data set. |
Why These Concepts Matter
Grasping these core techniques provides the framework for more advanced analysis, allowing for accurate predictions and informed decision-making. These methods are not just theoretical but are used daily to interpret real-world data across various fields. By mastering these key concepts, you are better prepared to tackle complex challenges and improve your problem-solving skills.
Understanding Descriptive Methods for Data Analysis
This section delves into the fundamental techniques used to summarize and interpret data. Descriptive methods are designed to provide an overview of key patterns, trends, and relationships within a dataset. By utilizing these tools, analysts can transform complex data into a more understandable format, enabling clearer insights and decision-making.
Key Measures for Summarizing Data
Descriptive analysis involves various measures that help represent data in a concise way. These include central tendency measures, such as the mean and median, as well as measures of dispersion, like range and standard deviation. The table below outlines the key metrics used to summarize data:
| Measure | Purpose | Calculation |
|---|---|---|
| Mean | Represents the average value of the dataset | Sum of all values / Number of values |
| Median | Shows the middle value in an ordered dataset | Middle value when data is sorted |
| Mode | Identifies the most frequent value in the dataset | Most common value |
| Range | Measures the spread between the highest and lowest values | Highest value – Lowest value |
| Standard Deviation | Indicates how spread out the values are from the mean | Square root of variance |
Applying Descriptive Methods Effectively
Using these descriptive methods effectively requires not only the correct calculation but also the appropriate application to the problem at hand. By selecting the right measure, you can gain a clearer understanding of the data’s central trend and variability. This ensures that the conclusions drawn from the data are both accurate and meaningful, guiding informed decision-making.
Solving Problems on Data Distribution
This section focuses on methods for understanding and solving problems related to how data is spread across different values. Distribution analysis helps identify patterns and trends, offering insights into the structure of a dataset. By understanding how data points are distributed, you can make more accurate predictions and informed decisions based on the observed trends.
Identifying Patterns in Data
When solving problems related to data distribution, the first step is recognizing the pattern or shape of the distribution. Is the data normally distributed, skewed, or does it have multiple peaks? By visually inspecting the data or using measures like skewness and kurtosis, you can gain a clearer understanding of its overall structure. Identifying these patterns allows for more accurate analysis and better decision-making.
Practical Application of Distribution Techniques
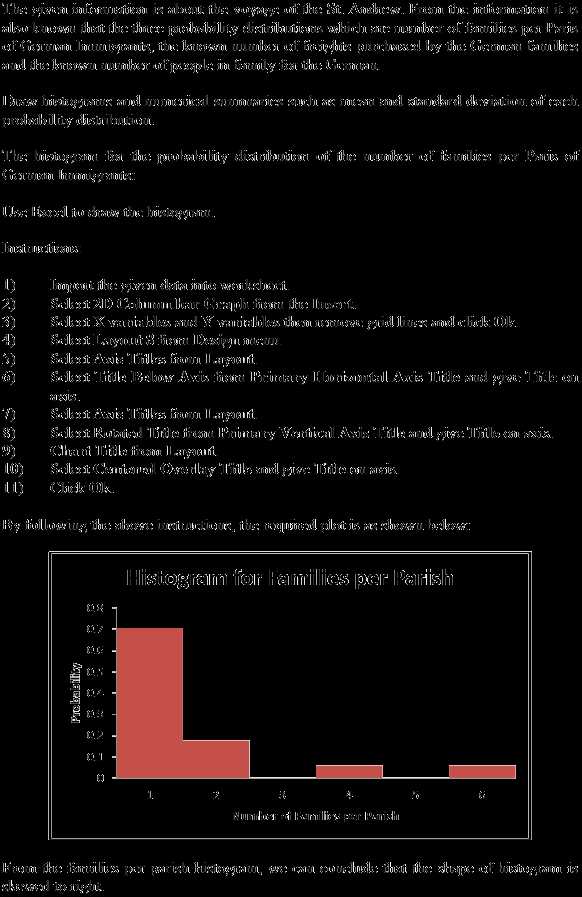
After identifying the distribution pattern, it’s important to apply the right techniques to analyze the spread of data. For example, calculating the range, variance, or standard deviation can provide a clearer picture of how much the data deviates from the central point. These tools help quantify the spread and variability of the dataset, offering a deeper understanding of its characteristics.
Interpreting Measures of Central Tendency
Understanding the central values within a dataset is crucial for summarizing and interpreting its overall pattern. Central tendency measures provide a way to capture the typical or most common value, offering a clear point of reference for comparing different data sets. These measures help identify trends and make it easier to communicate insights derived from the data.
There are three primary measures used to assess central tendency: the mean, median, and mode. Each offers a different perspective on the dataset’s central value, making it important to understand when to use each one depending on the nature of the data. The mean gives the average, the median reflects the middle value, and the mode identifies the most frequent occurrence.
Exploring Measures of Dispersion
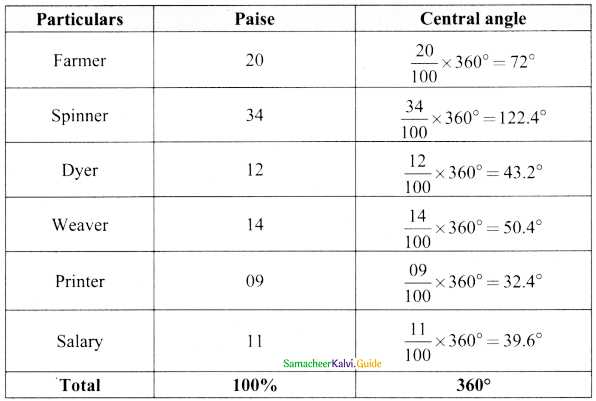
Dispersion measures are essential for understanding how spread out or varied the values in a dataset are. These metrics help evaluate the extent of variability and provide insights into the consistency or fluctuation within the data. By examining how widely data points differ from one another, you can make more informed decisions and draw meaningful conclusions about the overall dataset.
Common Methods for Measuring Spread
Several key methods are commonly used to quantify dispersion. The range, variance, and standard deviation are the most frequently applied measures. Each of these methods offers a different level of detail in understanding the extent of variation within a dataset:
| Measure | Purpose | Calculation |
|---|---|---|
| Range | Indicates the difference between the highest and lowest values | Highest value – Lowest value |
| Variance | Measures the average squared deviation from the mean | Sum of squared differences / Number of values |
| Standard Deviation | Provides the square root of the variance, indicating how spread out the data is | Square root of variance |
Interpreting Dispersion in Data
Once these measures are calculated, they allow for a deeper understanding of data variability. A small range or standard deviation suggests that the values are tightly clustered around the central tendency, while a large range indicates more significant variation. Understanding dispersion helps analysts determine the degree of certainty or uncertainty when making predictions or interpreting results from the data.
Applying Probability in Data Analysis
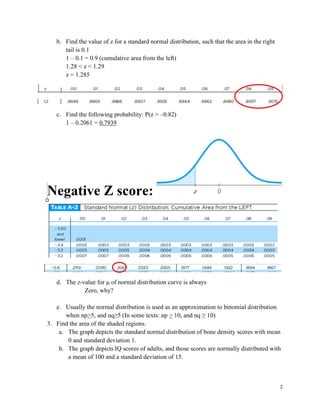
Probability plays a crucial role in evaluating and predicting outcomes based on observed data. By understanding the likelihood of different events, analysts can make more informed decisions and provide more accurate insights. Probability is especially valuable when working with uncertain or incomplete information, allowing for the assessment of risks and uncertainties in various scenarios.
Key Concepts in Probability
To apply probability effectively, it’s important to first understand some fundamental concepts. These include events, outcomes, and sample spaces, all of which are essential for calculating the likelihood of different occurrences. Below are some key terms to keep in mind when working with probability:
- Event: A specific outcome or a set of outcomes in an experiment.
- Outcome: The result of a single trial or observation.
- Sample Space: The set of all possible outcomes in a given experiment.
Calculating and Applying Probabilities
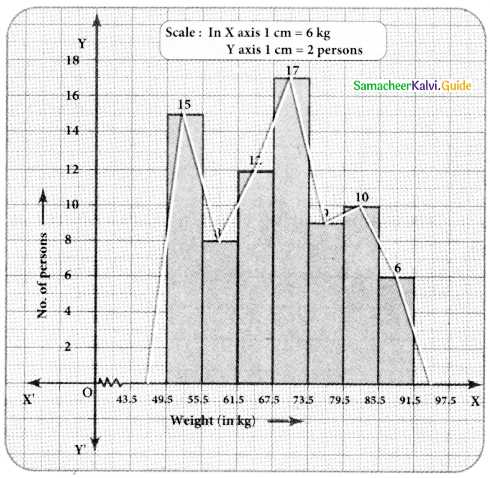
Once the basic concepts are understood, the next step is to calculate the probability of different events. This can be done using various formulas and methods, depending on the type of probability being calculated. Here are a few examples:
- Simple Probability: The likelihood of a single event occurring, calculated as the number of favorable outcomes divided by the total number of outcomes.
- Conditional Probability: The probability of an event occurring given that another event has already occurred.
- Joint Probability: The probability of two or more events occurring simultaneously.
By applying these probability concepts to real-world scenarios, analysts can better understand the chances of specific outcomes, leading to more reliable conclusions and predictions.
How to Analyze Data Sets
Analyzing data sets involves examining and interpreting data to uncover meaningful patterns, relationships, and trends. This process allows you to extract valuable insights that can inform decisions, guide research, or predict future outcomes. The goal is to transform raw data into actionable information by systematically organizing and evaluating it.
Steps in Data Analysis
To effectively analyze a data set, follow these essential steps:
- Data Collection: Gather the necessary data from reliable sources, ensuring that it is accurate, complete, and relevant to the problem at hand.
- Data Cleaning: Remove any inconsistencies, errors, or outliers from the data that could distort the analysis.
- Exploratory Data Analysis: Examine the data visually and statistically to identify initial patterns, distributions, and relationships.
- Data Modeling: Apply appropriate statistical or machine learning models to analyze the data and test hypotheses.
- Interpretation and Conclusion: Interpret the results of your analysis, drawing conclusions based on the findings and determining their implications.
Common Techniques for Analyzing Data
There are various techniques and tools that can be used to analyze a data set. Here are some commonly used methods:
- Descriptive Analysis: Summarizes the basic features of the data, such as mean, median, and mode, to provide a clear overview.
- Regression Analysis: Explores the relationship between variables to understand how one variable affects another.
- Correlation Analysis: Examines the strength and direction of the relationship between two or more variables.
- Hypothesis Testing: Uses statistical tests to determine whether the data supports a specific hypothesis or assumption.
By following these steps and applying the appropriate techniques, you can effectively analyze data sets and extract meaningful insights that can drive decision-making and problem-solving.
Identifying Statistical Relationships
Recognizing relationships between different variables is a fundamental part of data analysis. By understanding how one factor influences another, you can uncover patterns, make predictions, and improve decision-making. Identifying these connections requires a mix of visualization techniques and statistical methods to reveal how variables interact within a dataset.
Correlation and Causality
One of the most common ways to identify relationships is through correlation analysis. Correlation measures the strength and direction of the association between two variables. A strong positive correlation indicates that as one variable increases, the other also tends to increase. Conversely, a negative correlation suggests that as one variable rises, the other falls. However, it’s crucial to note that correlation does not imply causality – just because two variables are correlated, it does not mean one causes the other.
Visualization Techniques for Exploring Relationships
To better understand the relationships between variables, various visualization methods can be helpful:
- Scatter Plots: These graphs are used to display the relationship between two continuous variables, showing how they vary together.
- Line Graphs: Line graphs can help identify trends over time or in relation to other variables, providing a clear view of changes in data.
- Heatmaps: A heatmap is effective for identifying correlations between multiple variables, using color to represent the strength of the relationship.
By using these methods and tools, you can effectively identify and interpret statistical relationships, which can lead to deeper insights and better-informed decisions.
Using Graphs to Visualize Data
Graphs provide a powerful way to represent data visually, making it easier to detect patterns, trends, and relationships. Visualizations help convey complex information in a more digestible format, allowing for quicker analysis and more effective communication of findings. By transforming raw data into graphical representations, you can enhance your understanding and share insights in a clear, intuitive manner.
Types of Graphs for Data Visualization
There are various types of graphs used to visualize different kinds of data. Each type serves a unique purpose and is best suited for specific kinds of analysis. Below are some common types of graphs and their uses:
- Bar Charts: Useful for comparing categories or groups, bar charts display data with rectangular bars that represent values. These graphs work well for discrete data and show relative sizes of different categories.
- Line Graphs: Ideal for showing trends over time, line graphs connect data points with a line, making it easy to track changes and patterns across a time period or continuous range.
- Pie Charts: Used to represent proportions or percentages, pie charts divide a circle into segments, with each segment showing a part of the whole. This type is best for showing the relative sizes of categories within a dataset.
- Histograms: Similar to bar charts, histograms display the distribution of data across continuous intervals or bins. These graphs are ideal for showing the frequency distribution of numerical data.
Choosing the Right Graph for Your Data
When selecting a graph, it’s essential to consider the type of data you are working with and the insights you want to convey. The choice of graph influences how clearly the patterns and relationships in your data are represented. Here are some tips for choosing the right visualization:
- Consider the data type: Choose a graph type that best suits the nature of your data–categorical, continuous, or time-based.
- Keep it simple: Avoid overcomplicating your graph with too many elements. Focus on the key message and ensure the graph is easy to understand.
- Ensure clarity: Make sure the labels, axes, and legends are clear, and the graph is not cluttered with unnecessary information.
By selecting the appropriate graph for your dataset and presenting it effectively, you can significantly improve the clarity and impact of your data analysis.
Calculating Variance and Standard Deviation
To understand the distribution of data points within a dataset, two essential measures are often used: variance and standard deviation. These metrics provide insight into how spread out the values are, revealing the degree of variation or consistency within the data. Both are fundamental for analyzing data patterns and determining the predictability or volatility of a dataset. By calculating these values, one can assess whether the data points are clustered tightly around the mean or spread widely.
Variance: Measuring the Dispersion

Variance quantifies how far each data point is from the mean of the dataset. A higher variance indicates that the values are more dispersed, while a lower variance suggests that the data points are closely grouped around the mean. This metric is especially useful in determining the overall variability within a set of observations.
The formula for calculating variance is:
Variance (σ²) = Σ (xi – μ)² / N
Where:
- xi = each individual data point
- μ = the mean of the dataset
- N = the number of data points in the dataset
Standard Deviation: Interpreting Data Spread
Standard deviation is the square root of the variance and provides a more intuitive understanding of data dispersion. It is expressed in the same units as the original data, making it easier to interpret. A higher standard deviation indicates greater spread, while a lower standard deviation suggests that the data points are closer to the mean. Standard deviation is often used because it offers a clearer picture of data variability.
The formula for standard deviation is:
Standard Deviation (σ) = √Variance
Let’s now look at an example of how to calculate these values. Consider the following dataset: 2, 4, 6, 8, 10.
| Data Points | Deviation from Mean | Squared Deviation |
|---|---|---|
| 2 | -4 | 16 |
| 4 | -2 | 4 |
| 6 | 0 | 0 |
| 8 | 2 | 4 |
| 10 | 4 | 16 |
The mean of this dataset is 6. After calculating the deviations and squaring them, we get a total of 40. To find the variance, divide this sum by the number of data points (5). The variance is 8. Finally, by taking the square root of the variance, we obtain a standard deviation of approximately 2.83.
Understanding variance and standard deviation is crucial for interpreting the spread and consistency of data, and they are widely applied across many fields, such as finance, research, and quality control.
Understanding Confidence Intervals
In data analysis, it is often crucial to estimate the true value of a population parameter based on a sample. A confidence interval provides a range within which the true value is likely to fall, considering the inherent variability of the data. This range is accompanied by a level of confidence, which indicates how certain we are that the true value lies within the interval. Confidence intervals are widely used to quantify uncertainty and provide a more accurate view of the data than simply reporting a single point estimate.
The concept of a confidence interval revolves around the idea of statistical inference. Instead of claiming an exact value, a confidence interval acknowledges the natural variation in sample data and provides a range that likely contains the true population parameter. The width of the interval depends on factors such as sample size, variability, and the chosen confidence level. A wider interval implies more uncertainty, while a narrower interval suggests greater precision.
Typically, confidence intervals are expressed with a confidence level, such as 95% or 99%, which reflects the probability that the interval contains the true value. For example, a 95% confidence interval means that if the same sampling method were repeated many times, 95% of the intervals generated would contain the true population parameter.
Here’s an example of how to calculate a confidence interval for the mean of a sample. Let’s assume a sample mean of 50, a standard deviation of 10, and a sample size of 30. Using the formula for a confidence interval:
Confidence Interval = Mean ± (Z * (Standard Deviation / √Sample Size))
Where:
- Mean = 50
- Standard Deviation = 10
- Sample Size = 30
- Z = Z-score corresponding to the desired confidence level (for 95%, Z ≈ 1.96)
Substituting the values into the formula:
Confidence Interval = 50 ± (1.96 * (10 / √30))
The margin of error is calculated as 1.96 * (10 / √30), which is approximately 3.58. Therefore, the 95% confidence interval for the population mean is:
46.42 to 53.58
This means we can be 95% confident that the true population mean lies between 46.42 and 53.58. Confidence intervals are an essential tool in statistical analysis, allowing researchers to make more informed decisions and quantify the uncertainty in their estimates.
Using Regression for Predictions
In data analysis, regression techniques are powerful tools for understanding the relationship between variables and making predictions. By examining how one variable depends on others, regression allows us to model these connections and estimate future values based on known data. This approach is essential in many fields, from economics to healthcare, where predicting outcomes can drive decision-making and improve strategies.
At its core, regression involves identifying patterns in the data that indicate how one variable changes in response to another. The simplest form is linear regression, which assumes a straight-line relationship between the independent variable(s) and the dependent variable. By fitting a line to the observed data, we can predict the dependent variable for any given value of the independent variable.
For example, suppose you’re trying to predict house prices based on the size of the house. Using regression, you could determine the equation that best fits the data, such as:
Price = a + b * Size
Where a is the intercept and b is the slope of the line. Once the model is built, you can plug in the size of any house to estimate its price. The regression model doesn’t just provide predictions–it also helps quantify the strength and significance of the relationship between the variables, giving insights into which factors most influence the outcome.
Multiple Regression for Complex Predictions
When dealing with more than one independent variable, multiple regression comes into play. This method extends the idea of linear regression by considering multiple factors simultaneously. For instance, house prices might be influenced by not just size, but also location, age, and condition of the property. Multiple regression allows you to account for these factors together, providing a more nuanced prediction model.
The general form of a multiple regression equation looks like:
Price = a + b1 * Size + b2 * Location + b3 * Age
By analyzing the coefficients of each variable, you can assess how much each one contributes to the price. This approach allows for more accurate predictions, as it incorporates a broader range of factors.
Evaluating the Accuracy of Predictions

One of the key aspects of using regression for predictions is evaluating how well the model performs. Various metrics, such as R-squared and mean squared error, help assess the fit of the model to the data. A high R-squared value indicates that the model explains a significant portion of the variation in the dependent variable, while lower error metrics suggest more accurate predictions.
Regression is a versatile and widely used method for making predictions, allowing for both simple and complex models to be applied in various domains. By understanding the relationships between variables, analysts can make informed decisions and plan for future scenarios with greater confidence.
Importance of Sampling Methods
When analyzing large sets of data, it is often impractical or even impossible to collect information from every individual in a population. This is where sampling techniques come into play. By selecting a representative subset of the population, researchers can draw conclusions that are generalizable to the entire group without needing to survey everyone. The accuracy and reliability of these conclusions depend heavily on how the sample is chosen, making proper sampling methods crucial to the integrity of any study.
Sampling methods are used to ensure that the sample reflects the population’s characteristics as closely as possible. If done correctly, they can help produce reliable estimates, minimize biases, and increase the efficiency of data collection. However, poor sampling can lead to misleading results and incorrect conclusions. Understanding the different methods and their appropriate applications is vital for obtaining meaningful insights from data.
Types of Sampling Methods
There are several sampling techniques, each with its own advantages and limitations. Below are some of the most commonly used approaches:
- Random Sampling: Every individual in the population has an equal chance of being selected. This method is simple and effective for ensuring a truly representative sample.
- Stratified Sampling: The population is divided into subgroups (or strata) based on specific characteristics, and a sample is taken from each subgroup. This approach ensures that all relevant subgroups are adequately represented.
- Systematic Sampling: A sample is chosen using a fixed interval. For example, selecting every 10th person in a list. This method is easy to implement, but care must be taken to avoid patterns that could bias the sample.
- Cluster Sampling: The population is divided into clusters, and entire clusters are randomly selected for inclusion. This method is efficient for large, geographically dispersed populations.
- Convenience Sampling: Samples are chosen based on ease of access or availability. While cost-effective, this method is prone to significant bias and should be used with caution.
Evaluating Sampling Methods
To determine the reliability of a sample, several factors must be considered:
- Sample Size: Larger samples tend to yield more accurate estimates and reduce the impact of outliers or anomalies.
- Bias: Sampling methods should be designed to minimize bias. A biased sample can lead to inaccurate conclusions that do not reflect the true population.
- Cost and Time: Some methods are more resource-intensive than others. Researchers must balance the need for accuracy with available resources and time constraints.
In summary, choosing the right sampling method is essential for ensuring the validity of research findings. A well-selected sample provides a reliable representation of the population, enabling researchers to make informed decisions and draw meaningful conclusions from their data.
Practical Examples in Chapter 6
Applying theoretical concepts to real-world situations helps deepen understanding and enhances practical skills. In this section, we explore various examples that illustrate how data analysis methods can be used in everyday scenarios. These examples are designed to demonstrate the relevance of analytical tools and how they can be used to solve practical problems across different fields.
Example 1: Analyzing Test Scores

Imagine a classroom of students who have taken a final exam. By analyzing their scores, we can identify trends and gain insights into overall performance. Here’s how the different concepts are applied:
- Mean: The average score of all students is calculated to give an overall sense of the class’s performance.
- Median: The middle score is identified to see if there is any skewing in the distribution, particularly in the presence of outliers.
- Variance and Standard Deviation: These metrics are used to determine how spread out the scores are, helping to identify how consistent or varied students’ performances are.
Example 2: Customer Satisfaction Survey
Suppose a company conducts a survey to measure customer satisfaction. The survey results are collected and analyzed to determine the effectiveness of the company’s products and services. Key steps in the analysis include:
- Sampling: A random sample of customers is chosen to represent the larger customer base, ensuring that the results are not biased.
- Probability: The likelihood of customers giving certain ratings is calculated to help predict overall satisfaction levels.
- Confidence Intervals: These are used to estimate the true satisfaction level within a range of values, providing a sense of the uncertainty in the results.
Example 3: Market Research and Trends
Market researchers often rely on data analysis to predict future trends and consumer behavior. In this example, researchers might collect sales data from a variety of stores and use regression techniques to predict future sales. Key applications include:
- Linear Regression: A model is created to understand the relationship between factors such as advertising spend and sales volume.
- Correlation: The strength of the relationship between two variables is assessed to determine whether increasing one factor (like marketing budget) leads to increased sales.
- Data Visualization: Graphs and charts are used to represent the trends over time, making it easier to communicate the findings to stakeholders.
These practical examples demonstrate the power of analytical methods in making informed decisions and solving real-world problems. Whether it’s assessing student performance, gauging customer satisfaction, or predicting future trends, the ability to analyze data effectively is an invaluable skill in many fields.
Common Mistakes in Statistical Analysis
In data evaluation, certain errors often arise that can significantly impact the interpretation and reliability of results. These mistakes can distort findings, leading to misguided conclusions and incorrect decision-making. Recognizing and addressing common pitfalls is crucial for ensuring that data analysis is both accurate and meaningful.
One of the most frequent mistakes is misinterpreting the data. This happens when analysts incorrectly assume relationships between variables, such as confusing correlation with causation. It’s essential to understand that just because two factors appear to move together, it doesn’t necessarily mean that one is causing the other. Additionally, failing to consider the context or overlooking important variables can also result in misleading interpretations.
Another common issue arises from using improper sample sizes or non-representative samples. Small or biased samples can produce results that do not accurately reflect the broader population. It’s important to ensure that the sample is large enough and selected randomly to avoid skewed outcomes. This helps in making valid generalizations and ensures the robustness of the findings.
Ignoring the assumptions of statistical methods is another common mistake. Many analysis techniques assume certain conditions, such as normal distribution of data or independence between observations. When these assumptions are violated, the results may become unreliable. Before applying any method, it’s important to check whether the data meets these assumptions or consider alternative approaches if necessary.
Overfitting is another pitfall that can occur when models are too complex. In an attempt to capture every nuance in the data, analysts may create overly intricate models that work well with the training data but fail to generalize to new datasets. To avoid this, it’s crucial to balance model complexity with the risk of overfitting, ensuring that the model remains simple yet effective.
Finally, overlooking confounding variables can lead to incorrect conclusions about cause-and-effect relationships. Confounders are variables that influence both the independent and dependent variables, creating a false impression of a direct relationship. It’s essential to identify and control for these confounding factors to obtain accurate results and avoid biased interpretations.
By being mindful of these common mistakes and taking steps to prevent them, analysts can ensure that their findings are valid and reliable. A careful and methodical approach to data analysis helps produce accurate insights that can guide informed decisions and actions.
Reviewing Key Formulas and Equations
Understanding and applying the right formulas is essential for analyzing data effectively. These mathematical expressions are the foundation for making sense of numerical information and deriving meaningful insights. Whether you’re calculating averages, determining probabilities, or assessing variability, having a solid grasp of the key equations is crucial for accurate analysis and interpretation.
One of the most fundamental formulas is the calculation of the mean, which provides the central value of a dataset. The formula for the mean is:
Mean = (Sum of all values) / (Number of values)
This gives a measure of the typical or average value in a dataset. In addition to the mean, the variance and standard deviation are essential for understanding the spread or dispersion of the data. The formulas for variance and standard deviation are as follows:
Variance = Σ (Xᵢ – μ)² / N
Standard Deviation = √Variance
Where Xᵢ represents each data point, μ is the mean, and N is the total number of data points. These formulas allow you to measure the extent of variability in a dataset, with the standard deviation offering a more interpretable value due to its units being the same as the original data.
Another key formula involves probability, especially when making predictions or analyzing outcomes. The basic probability formula is:
Probability = (Number of favorable outcomes) / (Total number of outcomes)
This formula helps in calculating the likelihood of an event occurring and is foundational to making informed decisions based on chance.
For more advanced analysis, the regression equation is used to model relationships between variables. The most common form of regression is linear regression, represented as:
y = β₀ + β₁x + ε
Where y is the dependent variable, x is the independent variable, β₀ is the intercept, β₁ is the slope, and ε represents the error term. This equation helps in predicting the value of y based on the value of x.
By reviewing and practicing these key formulas and equations, you can enhance your ability to analyze data efficiently and accurately. These tools are essential for making data-driven decisions and for performing various types of analyses across different fields.