
In the world of mechanics, one of the key challenges is analyzing the movement of objects that follow a non-linear path. When an object is set into motion with an initial speed, the way it moves can be influenced by several factors, including gravity, initial velocity, and time. Understanding these dynamics requires careful analysis and calculation, especially when the object’s motion is not confined to a single plane.
To solve these types of problems, it’s essential to break down the movement into its components. By using both vertical and horizontal directions, we can analyze the various aspects of the object’s motion, providing insight into how it travels and how long it will remain in motion. This approach is not only useful for theoretical studies but also for real-world applications, such as predicting the trajectory of objects in various fields, including engineering and sports.
In this article, we will explore how to approach these types of challenges and walk through the steps to solve complex scenarios. With the right set of tools and methods, even the most intricate problems can be broken down into manageable parts. By understanding the core principles, anyone can master the art of calculating the motion of objects in a three-dimensional space.
3D Motion Challenges: Solving Horizontal Launch Scenarios
In the study of motion, certain scenarios require understanding how objects behave when they are set into motion in a three-dimensional space. This often involves examining how an object moves both vertically and horizontally under the influence of forces such as gravity. By breaking down these situations into simpler components, we can more easily predict the object’s trajectory and final position.
When solving these types of challenges, the key lies in applying the principles of motion to each direction separately. The vertical component is influenced by gravitational pull, while the horizontal component remains constant, assuming no other external forces act upon the object. By considering the time it takes for the object to fall and the distance it travels horizontally, we can derive solutions to the overall motion.
To approach these problems, we typically use equations of motion that allow us to calculate both the time of flight and the distance traveled. Understanding how these calculations work together enables us to solve for variables such as velocity, displacement, and duration of the object’s path. With these steps in mind, anyone can tackle the complexities of 3D motion involving horizontal movement.
Understanding the Basics of Motion in 3D
When analyzing the movement of an object through space, it is important to consider how various forces influence its motion. In many cases, objects follow a curved path due to the effects of gravity and initial speed. The key to understanding these motions is to break them down into simpler components, usually along two axes: vertical and horizontal. This approach allows us to predict the object’s behavior and calculate its final position after a certain period.
Key Principles of Motion
The first principle to understand is that the movement in each direction is independent of the other. The horizontal motion is unaffected by gravity, meaning that the object will continue moving at a constant speed unless acted upon by another force. Meanwhile, the vertical motion is governed by gravity, causing the object to accelerate downwards at a constant rate.
Breaking Down the Components
To calculate the overall motion, we use the concepts of time and velocity. By determining how long the object is in motion and how fast it is moving, we can solve for the distance traveled in both the horizontal and vertical directions. These components are then combined to give the full trajectory of the object, from its initial position to where it ultimately lands.
Key Concepts in 3D Motion Problems
When dealing with motion in three-dimensional space, understanding the underlying principles is crucial to solving related challenges. These scenarios often require analyzing an object’s behavior in both vertical and horizontal directions simultaneously. The key to mastering such problems is recognizing the independence of each axis and applying relevant equations to calculate position, velocity, and acceleration in both dimensions.
Below are some essential concepts for solving 3D motion challenges:
- Independence of Axes: Horizontal and vertical movements are analyzed separately, as the motion in one direction does not affect the other.
- Constant Horizontal Velocity: In the absence of external forces, an object’s horizontal speed remains constant throughout its motion.
- Acceleration Due to Gravity: The vertical motion is affected by a constant downward acceleration, typically denoted as 9.8 m/s² on Earth.
- Time of Flight: The duration of motion is a critical factor in determining both horizontal distance and vertical displacement.
- Vector Decomposition: Motion is often broken down into vector components, allowing for easier calculation of position and velocity at any given time.
By applying these concepts and using appropriate kinematic equations, one can predict the trajectory and behavior of objects moving through 3D space under the influence of gravity and initial velocity.
The Role of Horizontal Velocity
In motion analysis, the horizontal velocity of an object plays a fundamental role in determining how far it travels in the horizontal direction before reaching the ground. Unlike vertical motion, which is affected by gravitational acceleration, the horizontal component remains constant throughout the object’s flight, assuming no external forces such as air resistance are present. This constant velocity is crucial for calculating the range of the object’s motion.
Horizontal velocity does not change unless acted upon by an external force. This means that the speed at which an object moves in the horizontal direction remains steady from start to finish. The distance covered in this direction depends directly on the initial velocity and the time of flight, which is determined by the vertical motion.
In many real-world applications, such as predicting the trajectory of a thrown object or understanding the motion of a vehicle on a flat surface, the constant horizontal velocity is an essential factor. By combining this with the time spent in the air, one can calculate the total horizontal displacement, providing a complete picture of the object’s path through space.
Time of Flight in Horizontal Launches

The time an object spends in the air is a crucial aspect when analyzing its motion. For objects that begin their movement with an initial speed along a flat surface, the time of flight is primarily determined by the vertical motion. Since gravity affects the object as it falls, the duration of time the object remains airborne is influenced by how quickly it accelerates downwards.
Key Factors Influencing Time of Flight
Several factors contribute to the time an object remains in motion before reaching the ground. These include:
- Initial Height: The greater the starting height of the object, the longer it will take to reach the ground due to the increased distance it must fall.
- Acceleration Due to Gravity: On Earth, gravity pulls objects down at a constant rate of approximately 9.8 m/s², which directly affects the time of flight.
- Vertical Velocity: For objects with any initial vertical velocity, this component will also influence the total time spent in the air.
Calculating Time of Flight
To calculate the time of flight for an object moving in this way, we typically focus on the vertical displacement. Using the kinematic equation for vertical motion, we can determine the duration it takes for the object to fall to the ground. Once this time is known, we can use it to calculate how far the object travels horizontally, based on its constant horizontal speed.
Calculating Range for Horizontal Projectiles
Determining the range of an object moving through space involves calculating how far it travels in the horizontal direction before hitting the ground. In scenarios where the object begins its motion with an initial speed along a flat surface, its horizontal displacement depends on the time it stays in the air and its constant horizontal velocity. Understanding these relationships allows for precise predictions of the object’s final position.
Factors Affecting Range
The range of an object is influenced by several key factors:
- Initial Velocity: The speed at which the object is moving horizontally at the moment of release directly impacts the distance it will travel.
- Time of Flight: The longer the object stays in the air, the greater the horizontal distance it will cover. The time of flight is influenced by the object’s initial vertical position and gravitational acceleration.
- Acceleration Due to Gravity: While gravity does not affect horizontal motion directly, it determines the time the object is airborne, indirectly influencing the range.
Range Calculation Process
To calculate the range, we use the formula:
Range = Horizontal Velocity × Time of Flight
First, calculate the time of flight using vertical motion equations, considering the height from which the object starts its fall. Then, using the constant horizontal velocity, multiply it by the time to find the total distance the object will travel in the horizontal direction before landing.
Effect of Gravity on Horizontal Motion
Gravity plays a crucial role in determining the overall behavior of an object in motion. While it directly affects vertical displacement by pulling the object downward, it does not influence the horizontal speed of the object. However, gravity impacts the time an object spends in the air, which in turn affects how far the object will travel in the horizontal direction. Understanding this relationship is essential for accurate motion predictions.
When an object moves with an initial horizontal velocity, gravity causes it to fall at a constant rate, irrespective of its horizontal motion. The object’s downward acceleration due to gravity remains unchanged throughout its flight. The time spent in the air, determined by vertical motion, directly influences the horizontal distance covered by the object.
| Variable | Description | Impact of Gravity |
|---|---|---|
| Horizontal Velocity | Speed of the object in the horizontal direction | No impact–remains constant unless external forces act |
| Vertical Velocity | Speed of the object in the vertical direction due to gravity | Increases due to constant acceleration from gravity |
| Time of Flight | Duration for which the object remains in the air | Increases as the object falls under the influence of gravity |
| Range | Horizontal distance the object covers | Indirectly affected by gravity through its influence on time of flight |
In summary, gravity does not alter the object’s horizontal motion directly, but by affecting how long the object is in the air, it plays a significant role in determining the total horizontal displacement. This is why objects with higher initial vertical heights spend more time in the air, and thus cover a greater horizontal distance, assuming all other factors are constant.
Initial Speed and Its Impact on Trajectory
The initial speed at which an object begins its motion plays a significant role in shaping its overall trajectory. This starting velocity determines how far the object will travel in the horizontal direction before it hits the ground. While gravity affects the vertical motion, the horizontal speed remains unchanged unless acted upon by external forces. The relationship between initial speed and trajectory is key to predicting the object’s range and flight duration.
How Initial Speed Affects Horizontal Motion
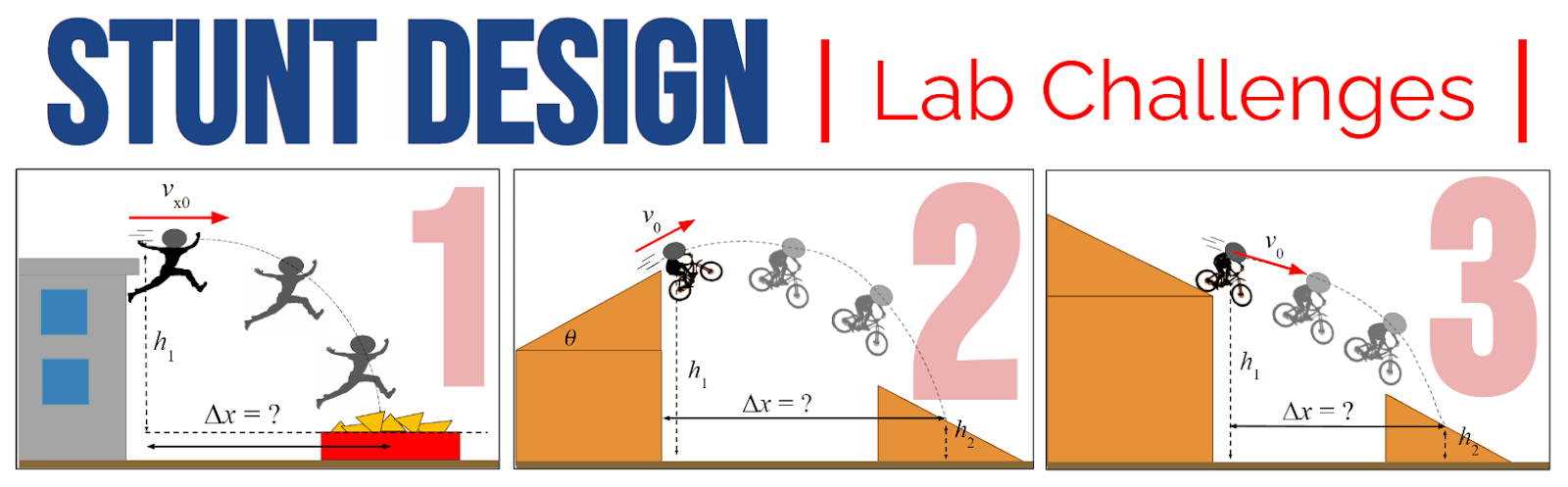
When an object is set in motion with a specific initial speed, its horizontal distance depends on both this speed and the time it remains airborne. A higher initial speed results in a greater horizontal displacement, as the object travels further in the same amount of time. The time spent in the air is influenced by vertical motion, which is governed by gravitational acceleration.
Calculating the Impact of Initial Speed
The impact of initial speed can be observed through its effect on the horizontal range. A higher velocity leads to a longer time of flight and, consequently, a larger horizontal distance. The relationship between speed and range can be described mathematically, taking into account both vertical and horizontal components of motion.
| Factor | Description | Impact of Initial Speed |
|---|---|---|
| Initial Speed | Starting velocity of the object in the horizontal direction | A higher initial speed results in a greater horizontal distance covered |
| Time of Flight | Duration the object stays in the air | Initially, speed does not affect time, but indirectly longer horizontal motion may suggest longer flight time |
| Horizontal Range | Total distance the object travels in the horizontal direction | Increases with higher initial velocity, as the object covers more ground during the time spent in the air |
In summary, initial speed is crucial in determining how far an object will travel before hitting the ground. By controlling this variable, one can predict the object’s horizontal range and assess how various speeds affect its overall trajectory. Understanding this relationship is essential for solving motion-related problems in real-world applications.
Using Vectors to Solve 3D Problems
In analyzing motion in three-dimensional space, vectors play a pivotal role in breaking down complex movements into manageable components. By representing both magnitude and direction, vectors provide a clear and organized method for solving problems involving multiple directions of motion, such as vertical and horizontal displacements. Using vectors simplifies the process of analyzing various forces and motion paths in 3D space.
Breaking Motion into Components
When solving for the displacement or velocity of an object in three dimensions, it’s common practice to resolve the motion into its individual components along the x, y, and z axes. This allows for a more straightforward application of the basic equations of motion. Vectors help isolate each component, making calculations easier and enabling a clearer understanding of the object’s path.
Applications of Vectors in 3D Motion
Vectors are especially useful in problems where an object moves in multiple directions simultaneously. For example, in a case where an object moves both vertically and horizontally, vectors can separate the motion into two orthogonal components. By analyzing each component individually and then combining them, the total displacement and velocity can be determined more efficiently. The same approach is used when calculating forces, velocities, or accelerations in various directions, ensuring accuracy in predictions and calculations.
In summary, vectors provide a powerful tool for solving problems involving motion in three-dimensional space. By decomposing motion into manageable components, vectors enable a more accurate and systematic approach to solving complex movement-related issues, ensuring that all factors influencing the object’s trajectory are considered.
Common Mistakes in Solving Projectile Problems
When solving motion-related issues, especially those involving objects in flight, several common errors can arise that lead to inaccurate results. These mistakes often stem from misunderstanding the relationship between horizontal and vertical components of motion, overlooking the influence of forces, or misapplying mathematical principles. Recognizing these pitfalls can help improve problem-solving accuracy and avoid misleading conclusions.
Neglecting the Independence of Horizontal and Vertical Motion

One of the most frequent mistakes is assuming that horizontal and vertical motions are dependent on each other. In reality, they operate independently of each other. The horizontal motion remains constant if no external horizontal force is acting on the object, while the vertical motion is solely influenced by gravity. Failing to treat these motions separately can lead to confusion, especially when determining the object’s trajectory or time in the air.
Misunderstanding the Effect of Gravity
Another common error involves misjudging the role of gravity in motion. Some may incorrectly assume that gravity impacts only the vertical velocity, but it also affects the object’s time of flight. Gravity causes the object to accelerate downward, which is critical for calculating the time it will spend in the air. Incorrectly assuming the object doesn’t experience gravity’s full effect can result in underestimating the time it takes to reach the ground and, therefore, the horizontal distance it covers.
Additionally, a mistake in calculating initial velocities or neglecting to account for air resistance (if relevant) can lead to misleading results. These small errors, though sometimes overlooked, can significantly impact the overall accuracy of the problem-solving process.
In summary, understanding the independence of horizontal and vertical motion, as well as properly accounting for the effects of gravity, is essential when solving flight-related problems. By avoiding these common mistakes, you can ensure more precise calculations and a better understanding of the object’s behavior in motion.
Step-by-Step Solution Process for 3D Projectiles
Solving problems involving objects moving in three-dimensional space requires a methodical approach to ensure all variables and forces are accounted for. The solution process typically involves breaking down the motion into manageable parts, focusing on both the horizontal and vertical components separately. This step-by-step method allows for a clearer understanding of how each factor influences the object’s trajectory and provides an accurate result.
Step 1: Identify Given Information
Before starting calculations, it’s essential to list all the known values. These include initial velocity, angle of motion (if applicable), height of release, and any forces acting on the object such as gravity. Recognizing what is given will guide the rest of the calculation process.
- Initial velocity (magnitude and direction)
- Height or distance of launch
- Acceleration due to gravity
- Air resistance (if relevant)
Step 2: Break Down Motion into Components
Next, divide the object’s motion into horizontal and vertical components. These components act independently, so treat them separately to simplify the calculations. For the horizontal motion, remember that the velocity remains constant if no horizontal forces are acting on the object. In contrast, the vertical motion will be influenced by gravity, causing acceleration over time.
- Calculate horizontal velocity using the given initial speed and angle (if necessary).
- Calculate vertical velocity using the same method, factoring in gravity for any change in height or speed over time.
Step 3: Apply the Kinematic Equations
Use the appropriate kinematic equations to calculate the object’s displacement, velocity, and time of flight. For horizontal motion, the distance traveled can be found by multiplying the horizontal velocity by the time of flight. For vertical motion, use equations that include gravity to determine how long the object is in the air and how far it falls during its trajectory.
Step 4: Combine Results
Once the horizontal and vertical motions have been calculated, combine the results to find the overall trajectory. The total distance traveled is the combination of the horizontal distance and the vertical displacement. By using vector addition, you can determine the object’s final position and analyze its path in three-dimensional space.
In conclusion, breaking down the motion into smaller components, applying the correct equations, and carefully combining the results are key steps in solving any three-dimensional motion problem. This systematic approach ensures that all factors are considered and the solution is as accurate as possible.
Impact of Air Resistance on Horizontal Motion
When an object moves through the air, it experiences forces that can significantly alter its path. One of the most crucial of these forces is air resistance, which opposes the motion of the object and slows it down over time. While objects in motion are generally expected to maintain a consistent speed in the absence of external forces, air resistance causes a continuous loss of velocity, especially in the horizontal direction. Understanding how this force affects motion is essential for accurate predictions of the object’s trajectory and displacement.
Unlike vertical motion, where gravity has a clear and predictable effect, horizontal motion is more complex when air resistance is considered. The force of air resistance increases with the velocity of the object, meaning that the faster it moves, the more drag it experiences. This results in a gradual reduction in horizontal speed as the object travels through the air.
The impact of air resistance can be illustrated through the following points:
- Velocity Reduction: As the object moves, air resistance reduces its horizontal velocity over time, leading to a shorter horizontal distance traveled.
- Non-linear Deceleration: The deceleration due to air resistance is not constant but increases as the object speeds up.
- Dependence on Shape and Surface Area: The amount of air resistance depends on the shape, size, and texture of the object. For example, a streamlined object experiences less drag than a rough or irregularly shaped one.
- Significant for High-Speed Motion: The effect becomes more pronounced at higher velocities. For slower-moving objects, air resistance may have minimal impact.
Overall, air resistance alters the idealized path of an object by gradually slowing its horizontal motion, which must be accounted for in more precise calculations of displacement and time of flight. Its impact is more significant at higher speeds and for larger objects, making it a key factor to consider in real-world scenarios where accuracy is essential.
Using Graphs to Visualize Projectile Motion
Graphs provide a powerful tool for understanding the dynamics of an object in motion, especially when it comes to illustrating the complex relationships between various factors such as velocity, acceleration, and time. By plotting key variables, such as horizontal distance, vertical height, and speed, one can gain insight into the behavior of an object as it moves through space. These visual representations help simplify complex calculations and make it easier to predict the path of the object.
When analyzing motion, two key graphs are typically used: one for horizontal motion and another for vertical motion. Each graph provides valuable information about how the object behaves over time, including its speed, position, and acceleration in both directions. The resulting visualizations not only demonstrate how the object’s motion progresses but also reveal the interplay between forces such as gravity and air resistance.
Horizontal Motion Graphs
In the case of horizontal motion, the graph typically shows a constant velocity, assuming no significant forces, such as air resistance, are acting on the object. The horizontal distance increases linearly with time, and the slope of the graph represents the constant speed. Since there is no acceleration in the horizontal direction (in an idealized model), the velocity remains unchanged throughout the motion.
Vertical Motion Graphs
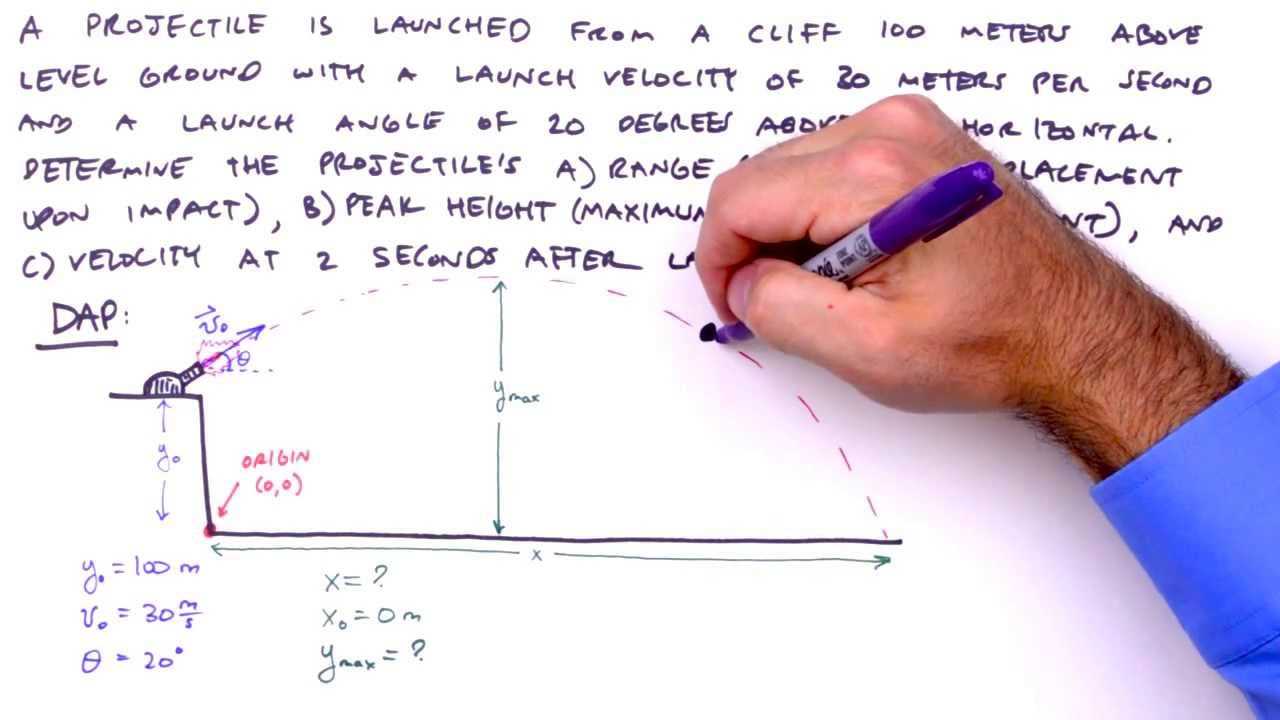
Vertical motion, however, is influenced by gravity and typically results in a curved graph. The vertical velocity starts at zero (if the object is initially at rest) and increases as the object accelerates downward due to gravitational pull. The shape of the graph is parabolic, reflecting the object’s increasing speed as it moves downward. The acceleration due to gravity causes a consistent increase in velocity, which can be seen as a straight line when plotted against time.
By combining both graphs, one can gain a comprehensive understanding of how an object moves in two dimensions, allowing for a better prediction of its flight path and landing point. These graphs not only aid in theoretical calculations but also provide a clear and intuitive way to grasp the principles of motion in a visual format.
How to Set Up a Problem Correctly
When tackling any motion-related task, setting up the problem correctly is essential to ensuring that all necessary factors are considered and calculations are accurate. A clear and structured approach helps avoid common mistakes and allows for a better understanding of the scenario. The first step is to gather all the information given, including initial conditions such as starting speed, angles, and other relevant details. From there, it’s important to break the problem into smaller components, such as horizontal and vertical motions, and apply the appropriate equations to each.
1. Identify Known Values
Before beginning any calculations, it’s crucial to identify what information is provided in the scenario. Typically, the problem will provide key details such as initial speed, height, or time of flight. These values will form the foundation for solving the task. Organizing this information into a table can help visualize what’s given and what needs to be determined.
| Known Information | Value |
|---|---|
| Initial Speed | 15 m/s |
| Initial Height | 20 m |
| Acceleration due to Gravity | 9.8 m/s² |
2. Break the Motion into Components
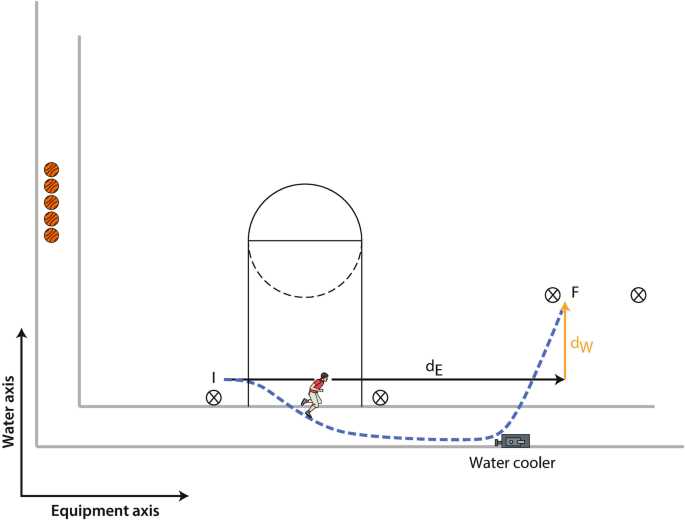
Once the known values are identified, it’s time to separate the motion into horizontal and vertical components. This step simplifies the problem and ensures that the correct equations are used for each direction. For horizontal motion, focus on constant velocity, while for vertical motion, use equations that account for acceleration due to gravity. Treating each component independently will allow for easier manipulation of the equations and prevent confusion.
By carefully organizing the information, understanding the forces at play, and breaking the problem into manageable components, solving the task becomes much more straightforward. These initial steps are key to a successful solution process and can help avoid mistakes in more complex calculations.
Application of Kinematic Equations in 3D
In motion analysis, understanding how objects behave in three dimensions is crucial for accurate predictions. By applying kinematic equations, we can describe the movement of an object through space, considering both horizontal and vertical motions. These equations provide a systematic way to calculate key parameters such as velocity, displacement, and time, using the forces acting on the object. The application of these equations becomes particularly important when dealing with more complex scenarios, such as when motion occurs in multiple directions simultaneously.
To solve problems involving three-dimensional motion, the first step is to decompose the motion into its individual components. Typically, this means separating the horizontal and vertical directions, allowing for the application of the appropriate kinematic equations to each. For horizontal motion, the object’s velocity remains constant unless affected by external forces, while vertical motion is influenced by acceleration due to gravity.
For each component, the following kinematic equations can be applied:
- For horizontal motion: v_x = v_x0 (constant velocity)
- For vertical motion: y = y0 + v_y0 * t – 1/2 * g * t² (acceleration due to gravity)
By solving these equations for each direction separately, we can determine the overall trajectory of the object and make accurate predictions about its future position. This method simplifies the problem, ensuring that each component is treated independently but in relation to the others, leading to a clear and organized approach to solving motion problems in three dimensions.
Solving for Velocity Components
When dealing with motion in two or more dimensions, it is essential to break down the velocity into its individual components. This process allows for a clearer understanding of how an object moves in each direction. By separating the velocity into horizontal and vertical components, we can apply the appropriate equations for each direction, simplifying the problem and making it easier to solve. This method is especially useful in cases where forces act in different directions, as it enables us to treat each direction independently while still considering their combined effects on the object’s overall motion.
To solve for the components of velocity, we use trigonometric relationships. For an object moving at an angle, the velocity can be decomposed into two parts: one along the x-axis (horizontal direction) and one along the y-axis (vertical direction). The velocity components can be calculated using the following formulas:
- Horizontal velocity component: v_x = v * cos(θ)
- Vertical velocity component: v_y = v * sin(θ)
In these equations, v represents the object’s total velocity, and θ is the angle at which it is moving relative to the horizontal. By using these formulas, you can determine the individual components of velocity and analyze the motion along each axis separately. Once the components are known, they can be used to calculate other parameters, such as displacement, time, and acceleration, using the relevant kinematic equations.
In summary, solving for velocity components is a crucial step in analyzing two- or three-dimensional motion. It allows for a more manageable approach to complex problems by simplifying the motion into horizontal and vertical components, each of which can be treated independently to determine the overall trajectory of the object.
Real-World Examples of Horizontal Motion
Understanding how objects behave when they are set into motion in a straight line is essential in many real-world applications. Horizontal motion is a fundamental concept, and its effects can be observed in a variety of everyday situations. By examining how objects move in such scenarios, we can better grasp the principles that govern their trajectories and make more informed decisions in practical settings.
Example 1: Dropping an Object from a Moving Vehicle
Consider a situation where an object is dropped from a car moving at a constant speed. From the perspective of an observer inside the car, the object would seem to fall straight down. However, from the perspective of an observer outside the car, the object follows a curved path as it retains the forward velocity of the car while falling toward the ground. This scenario demonstrates how an object’s horizontal motion continues even after it is released, due to its initial speed matching the vehicle’s velocity.
Example 2: Throwing a Ball from a Moving Cart
Another example can be seen when a ball is thrown from a cart moving along a track. If the ball is thrown forward with the same speed as the cart’s movement, it will appear to travel straight ahead from the perspective of an observer on the cart. For an observer on the ground, however, the ball will follow a curved path due to its horizontal speed from the moving cart and its vertical fall due to gravity. The principles of horizontal motion are crucial in understanding how the ball’s trajectory is influenced by its initial velocity and the forces acting on it.
These real-world examples highlight how horizontal motion impacts the movement of objects in dynamic environments. By understanding the fundamental principles that govern this type of motion, we can predict and analyze the behavior of objects more accurately in both everyday and specialized contexts.
Additional Resources for Further Learning
For those looking to deepen their understanding of motion, velocity, and the forces involved in real-world applications, there are a variety of resources available. These resources provide detailed explanations, practice exercises, and interactive tools to help solidify the concepts and offer broader perspectives on the topic. Whether you are a beginner or someone with a foundational understanding, these materials will expand your knowledge and help you apply the principles effectively.
Online Courses
Interactive learning platforms offer comprehensive courses that cover a wide range of topics related to motion, forces, and kinematics. Some excellent platforms to explore include:
- Coursera – Offers courses from top universities, focusing on practical applications of motion in various contexts.
- Khan Academy – Features beginner-friendly lessons on motion, including videos, practice exercises, and quizzes.
- edX – Provides access to free and paid courses, including in-depth studies of mechanics and related fields.
Books and Texts
For those who prefer traditional reading, there are numerous textbooks and guides that explore the concepts of motion in greater depth. Recommended books include:
- “Understanding Physics” by Isaac Asimov – A clear, accessible introduction to the fundamental concepts of motion and forces.
- “Classical Mechanics” by Herbert Goldstein – A more advanced textbook that delves into the mathematical foundations of motion and dynamics.
- “Fundamentals of Physics” by David Halliday and Robert Resnick – A well-known resource that covers a wide range of concepts in physics, with extensive practice problems.
Interactive Simulations and Tools
For hands-on learners, interactive tools and simulations can be invaluable in visualizing complex motions and understanding the underlying principles. Some popular resources include:
- PhET Simulations – Provides free, interactive simulations that allow users to experiment with and explore various physical concepts.
- Algodoo – A physics-based simulation tool that lets you create and manipulate dynamic scenarios to observe the effects of forces and motion.
- GeoGebra – Offers dynamic mathematics tools that can be used to model and analyze the motion of objects in different settings.
By utilizing these resources, learners can build a stronger grasp of motion, forces, and their applications in both theoretical and practical contexts. Whether through formal courses, self-study books, or interactive tools, there are many ways to continue exploring and mastering the subject.