
Mathematical problem sets often require a combination of theoretical knowledge and practical application. The solutions to these exercises help reinforce understanding and provide insight into complex ideas. Mastering these tasks not only boosts confidence but also improves critical thinking and analytical skills.
Through detailed explanations and structured methods, students can better grasp how to approach each problem. Focusing on core principles allows for a deeper comprehension of the material, making even the toughest challenges more manageable. Building a strong foundation in these topics ensures that learners are well-prepared for future lessons.
Whether you’re revisiting basic techniques or tackling more advanced challenges, the key is consistent practice and clarity in reasoning. Developing an organized approach will aid in accurately solving problems and enhancing overall performance in mathematical studies. Clarity and perseverance are the cornerstones of success in mastering these tasks.
Practice B Geometry Answer Guide
In this section, we will walk through a series of solutions that are designed to improve your problem-solving skills. Each explanation is crafted to clarify the steps involved in reaching the correct conclusions. Understanding the logic behind these exercises is crucial for strengthening your mathematical abilities.
Step-by-Step Breakdown
For each problem, we begin by identifying the given information and then proceed through logical steps to arrive at the solution. By following a clear and methodical process, you can ensure that no crucial detail is overlooked. This approach not only helps in finding the right answer but also in reinforcing key concepts.
Tips for Effective Problem Solving
While working through these problems, it’s important to stay organized and keep track of your work. Using diagrams or sketches can help visualize the relationships between different elements. Additionally, reviewing the steps after reaching a solution can often reveal shortcuts or alternative methods that further streamline your process.
Key Concepts in Geometry Practice B
To effectively tackle mathematical challenges, it’s essential to understand the core principles that underpin the problems. In this section, we will focus on the fundamental ideas that are critical for solving complex tasks. These concepts form the foundation of the skills needed to succeed and build confidence in tackling progressively difficult exercises.
Understanding Shapes and Their Properties

A solid grasp of geometric shapes and their properties is crucial. By learning about different forms, their angles, sides, and relationships, you will be better equipped to solve various types of problems. Recognizing patterns and knowing how to apply relevant theorems can drastically simplify the process of finding solutions.
Using Measurement Techniques Effectively
Measurement is another key aspect that must be mastered. Whether dealing with lengths, areas, or volumes, understanding the formulas and how to apply them is fundamental. Accurate measurements are the backbone of correct solutions, and knowing when and how to use them is vital for success in these exercises.
Step-by-Step Solutions for 1.4 Problems
Breaking down complex problems into manageable steps is an effective strategy for mastering mathematical tasks. This section outlines a methodical approach to solving various exercises. By following a clear sequence of operations, you can ensure that each part of the problem is addressed properly, leading to accurate results.
Identifying Key Information
The first step in solving any problem is recognizing and organizing the given data. Carefully review the information provided and isolate the key components needed to proceed. Whether it involves identifying shapes, angles, or other elements, understanding what’s available allows you to create a plan of action for solving the task.
Applying Relevant Formulas
Once the problem is understood, applying the correct formulas is essential. Make sure to choose the right equation for the situation, whether it involves calculating areas, angles, or relationships between different components. Following a systematic approach ensures that all calculations are accurate and that nothing is overlooked during the process.
Understanding Geometry Formulas for Practice B
Mathematical formulas serve as essential tools for solving various types of problems. In this section, we will explore the most commonly used equations in this field. A deep understanding of these formulas is key to accurately calculating areas, volumes, and relationships between geometric elements. Knowing when and how to apply them is crucial for efficient problem solving.
Basic Formula Overview
Each formula has a specific purpose, whether it relates to the calculation of areas, perimeters, or angles. Here is a quick overview of some fundamental formulas:
| Shape | Formula | Description |
|---|---|---|
| Rectangle | Area = Length × Width | Used to calculate the area of a rectangle. |
| Triangle | Area = 1/2 × Base × Height | Used to find the area of a triangle. |
| Circle | Area = π × Radius² | Used for calculating the area of a circle. |
| Square | Area = Side² | For calculating the area of a square. |
Using Formulas in Context
It is important to understand the context in which these formulas apply. For example, knowing how to derive the perimeter of a polygon, or how to find the angle between intersecting lines, requires not only familiarity with the formulas but also the ability to recognize the correct scenario in which they should be applied. Regular practice with different problems enhances the ability to identify the relevant formulas quickly.
Common Mistakes in Practice B Geometry

When solving mathematical problems, it’s easy to make errors that can lead to incorrect results. Recognizing common mistakes and understanding their causes can help improve accuracy and efficiency. By identifying and avoiding these pitfalls, students can strengthen their problem-solving skills and approach challenges with greater confidence.
Misinterpreting the Problem
One of the most frequent mistakes occurs when the problem is not fully understood. Failing to properly identify the given information or misinterpreting the question can lead to incorrect conclusions. Taking the time to carefully read and analyze the problem ensures that all necessary details are considered before proceeding with a solution.
Incorrect Application of Formulas
Another common error is using the wrong formula or applying it incorrectly. It’s essential to choose the correct equation for the situation and to use it accurately. Whether it involves confusion between area and perimeter formulas or improper use of trigonometric relations, double-checking each formula used can help prevent mistakes.
How to Approach 1.4 Geometry Questions
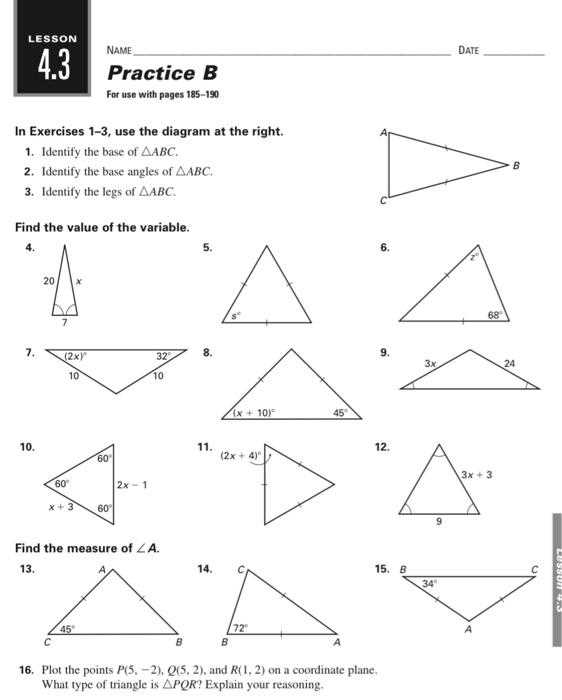
Effective problem solving requires a strategic approach, especially when dealing with mathematical tasks. By breaking down each question into manageable parts and following a systematic method, you can ensure that each step is clear and logical. Understanding the structure of a problem allows you to focus on the key elements and avoid common mistakes.
Step 1: Analyze the Problem
The first step is to carefully read through the problem and identify all relevant details. Look for given information, such as measurements, angles, or other important values. Organize this information visually or mentally, and determine what is being asked for. By understanding the context and what needs to be found, you will be better prepared to select the appropriate approach.
Step 2: Choose the Right Tools
Once the problem is clearly understood, it’s time to decide on the best method to solve it. This might involve applying a specific formula, using geometric relationships, or employing logical reasoning. Below is a table of some common methods and their use cases:
| Method | When to Use | Example |
|---|---|---|
| Pythagorean Theorem | Right triangles with known leg lengths | Finding the hypotenuse |
| Area Formula | For polygons (squares, rectangles, etc.) | Calculating the area of a rectangle |
| Angle Sum Theorem | Triangles and polygons | Finding missing angles in polygons |
By selecting the right technique, you ensure that the process remains straightforward and efficient.
Tips for Solving Geometry Problems Effectively
Solving mathematical problems can be challenging, but with the right strategies, it becomes a more manageable task. Developing a systematic approach helps in breaking down complex questions into simpler steps. By focusing on the fundamentals and avoiding common pitfalls, you can improve your accuracy and efficiency in problem-solving.
Organize Your Work
Before diving into calculations, it’s crucial to organize all the information clearly. Start by writing down the known values and identifying what needs to be found. Drawing diagrams or sketches can significantly aid in visualizing relationships and clarify how different elements interact. Clear organization not only makes it easier to follow your process but also helps spot errors early on.
Double-Check Your Calculations
It’s easy to overlook small mistakes, especially during lengthy calculations. Always take a moment to review your work. Check your formulas, ensure all values are correctly plugged in, and verify your math. Double-checking your steps will prevent simple errors from affecting the final result and ensure the solution is accurate.
Visual Aids for 1.4 Geometry Answers
Effective visual tools can significantly enhance understanding and problem-solving skills. By integrating different types of diagrams, charts, and illustrations, learners can improve their ability to grasp complex concepts. These aids help transform abstract ideas into tangible representations, making it easier to visualize relationships and solve related tasks.
Various methods can be employed to assist with comprehension:
- Diagrams: Simplified drawings highlighting key points and angles allow for easier analysis of shapes and their properties.
- Graphs: Coordinate systems or graphing tools help depict relationships between variables and spatial arrangements.
- Interactive Tools: Digital platforms where users can manipulate shapes and measurements foster hands-on learning.
- Step-by-Step Visual Guides: These offer sequential visuals that break down complex procedures into manageable steps.
Incorporating these tools into learning not only aids in comprehension but also boosts confidence in tackling various challenges.
Geometry Review for Practice B Answers
Reviewing foundational concepts is essential for tackling more advanced problems. A strong grasp of basic principles allows for smoother application in complex scenarios. Understanding the core ideas and practicing their usage is key to solving related tasks efficiently and accurately.
This review focuses on revisiting important topics and methods, providing clarity and reinforcing the knowledge needed to solve typical challenges:
- Basic Shapes and Properties: Familiarity with common figures and their characteristics forms the basis for solving related problems.
- Angles and Relationships: A clear understanding of various angle types and how they interact within different configurations is essential.
- Measurement Techniques: Accurately calculating dimensions, areas, and volumes remains crucial in almost all tasks.
- Transformations: Knowing how to apply shifts, rotations, and reflections helps in understanding the movement of shapes.
By revisiting these concepts, learners can approach challenges with more confidence and accuracy.
Common Strategies for Geometry Success
Achieving success in spatial reasoning tasks involves more than just memorizing formulas. It requires a strategic approach to problem-solving that combines analytical thinking with practical techniques. By mastering essential skills and applying them consistently, learners can improve their proficiency and confidence in solving complex problems.
Below are key strategies that can help enhance performance:
| Strategy | Description |
|---|---|
| Understand Key Concepts | Grasping the fundamental principles behind shapes, angles, and transformations helps in quickly identifying solutions. |
| Visualize the Problem | Drawing diagrams or mentally picturing the problem can clarify relationships and guide toward the correct solution. |
| Break Down Complex Problems | Breaking problems into smaller, manageable steps prevents overwhelm and ensures accuracy in each part of the solution. |
| Use Logical Reasoning | Applying logical steps, such as the properties of symmetry and congruence, can lead to quick conclusions. |
| Practice Regularly | Frequent practice reinforces concepts, helping to internalize methods and improve speed and accuracy. |
Incorporating these strategies into study routines can significantly improve problem-solving skills and lead to greater success in tackling various tasks.
Checking Your Answers in Geometry
Verifying the correctness of your solutions is an essential step in mastering spatial reasoning tasks. Ensuring that each step is accurate and logical can prevent mistakes and improve the overall understanding of concepts. A careful review process helps confirm that no errors were made and that the solution is consistent with the principles at hand.
Here are some effective methods for double-checking your work:
- Revisit Key Steps: Go over each calculation and logical step to ensure nothing was overlooked.
- Check for Consistency: Verify that your results align with expected relationships and known properties of shapes.
- Use Alternative Methods: If possible, solve the problem using a different approach to confirm the result.
- Estimate and Compare: Make rough estimates of the solution and compare them with your final answer to spot any obvious errors.
- Verify Units and Measurements: Ensure that the units and dimensions in your solution match the problem’s requirements.
Taking the time to review not only confirms accuracy but also deepens your understanding of the material, leading to greater confidence in future tasks.
Advanced Geometry Tips for Practice B
As tasks become more complex, advanced techniques and strategies become essential for solving problems efficiently. Building a deeper understanding of the underlying principles and applying sophisticated methods can help solve even the most challenging scenarios. These tips will help refine your skills and enhance your problem-solving ability.
Key Strategies for Success
- Use Theorems Effectively: Familiarize yourself with key theorems and properties that can simplify problems, such as the Pythagorean theorem or properties of similar triangles.
- Focus on Symmetry: Recognizing symmetry in shapes can reduce the complexity of a problem by allowing you to apply patterns or shortcuts.
- Leverage Algebraic Methods: Incorporating algebraic techniques, such as solving systems of equations, can help handle problems involving coordinates and geometric figures.
- Work Backwards: Sometimes starting from the desired result and working backwards can provide insight into how to approach a problem.
Practical Approaches for Problem Solving

- Draw Detailed Diagrams: Accurately sketching the problem can often reveal hidden relationships or dimensions that are not immediately obvious.
- Consider Special Cases: Analyzing specific instances or extreme cases can sometimes lead to general solutions that apply to a broader set of problems.
- Break Down Complex Figures: Decompose complicated shapes into simpler parts that are easier to analyze and solve.
- Check for Precision: Pay close attention to measurements, especially when working with areas or angles, as small errors can lead to larger mistakes.
Applying these advanced strategies not only helps with tackling complex problems but also improves overall understanding of geometric concepts, leading to greater success in solving difficult tasks.
Helpful Resources for Geometry Students
Access to the right tools and materials can make a significant difference in mastering spatial reasoning and mathematical concepts. Whether you’re looking to reinforce foundational knowledge or tackle more complex problems, there are numerous resources that can help you improve your skills and understanding.
Here are some useful resources that can assist students in mastering key concepts:
- Textbooks and Study Guides: Well-structured books and guides provide step-by-step explanations, practice problems, and illustrations that simplify complex ideas.
- Online Learning Platforms: Websites and apps offering interactive lessons and tutorials can help students visualize concepts and work through problems at their own pace.
- Video Tutorials: Watching expert explanations on platforms like YouTube can offer alternative ways to understand difficult topics.
- Mathematical Software: Programs that allow for the manipulation of shapes and measurements provide a hands-on approach to learning and visualizing abstract concepts.
- Practice Worksheets: Printed or digital worksheets with a variety of problems allow for additional practice and reinforcement of skills.
- Study Groups and Forums: Collaborating with peers in study groups or engaging in online forums provides opportunities for discussion, clarification, and problem-solving together.
Using a combination of these resources can provide a well-rounded approach to mastering the material and improve performance in problem-solving tasks.
Improving Geometry Skills with Practice B
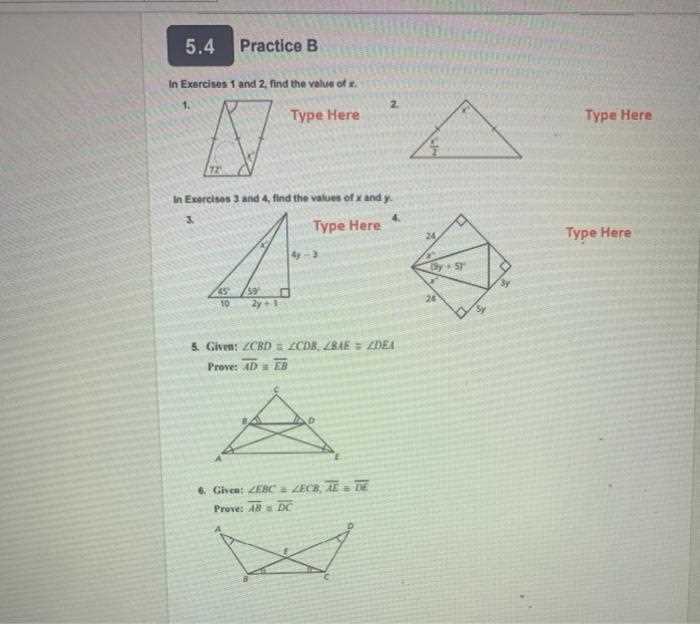
Consistent practice is a key factor in developing proficiency in spatial reasoning and mathematical problem-solving. By working through various exercises and applying learned concepts, students can strengthen their understanding and improve their ability to solve complex challenges. Practice not only reinforces knowledge but also builds confidence in tackling new problems.
Focus on Key Areas for Improvement
- Mastering Fundamental Theorems: Understanding the core principles is essential for approaching more complex tasks. Regularly reviewing these theorems helps solidify your foundation.
- Strengthening Visualization Skills: Visualizing shapes, angles, and transformations helps connect abstract concepts to real-world applications. Drawing diagrams and using models can improve spatial awareness.
- Applying Problem-Solving Strategies: Developing a step-by-step approach to each problem allows for more efficient and accurate solutions. Identify patterns, simplify problems, and break them into smaller parts.
Benefits of Regular Practice
- Enhanced Speed: The more you practice, the quicker you will recognize patterns and solve problems, allowing for faster completion of tasks.
- Increased Accuracy: Frequent exercises help reduce errors by reinforcing correct methods and calculations.
- Confidence Boost: Successfully solving a variety of problems builds confidence and prepares you for more challenging exercises.
By focusing on these areas and making practice a routine, students can significantly improve their performance and deepen their understanding of spatial relationships and mathematical reasoning.