In the world of mathematics, understanding complex expressions and operations is crucial for solving a wide range of problems. By developing a strong grasp of these concepts, learners can enhance their problem-solving abilities and build a solid foundation for more advanced topics.
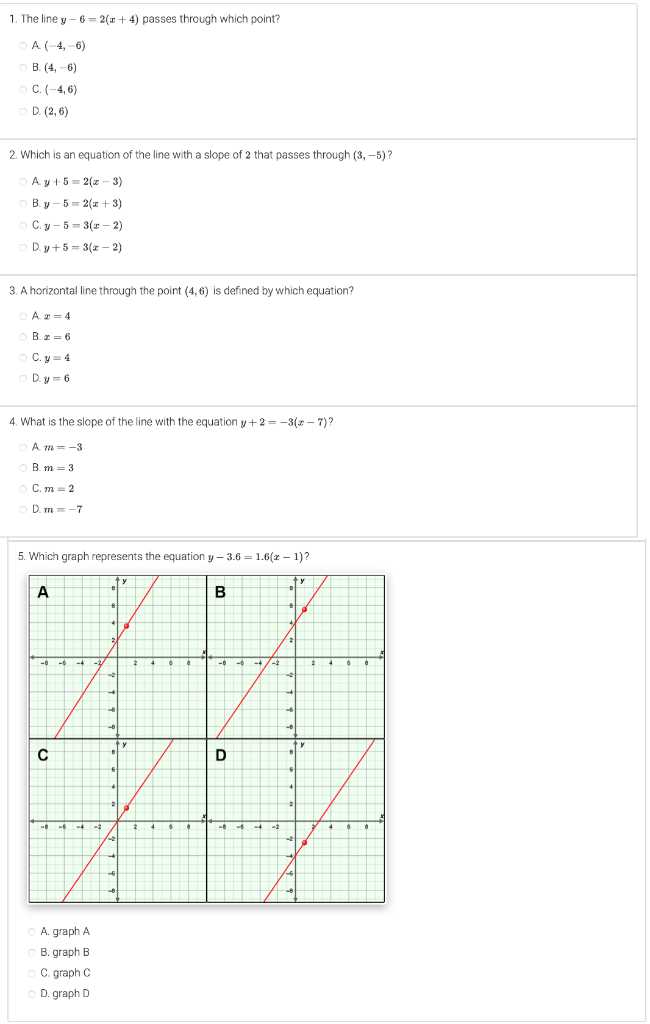
Throughout this section, we focus on essential techniques that will help you navigate through intricate equations and mathematical relationships. With a clear approach and well-practiced methods, you will be able to tackle various types of problems with confidence and precision.
By familiarizing yourself with the right strategies and honing your skills, you will gain the tools needed to accurately approach and resolve mathematical challenges. This knowledge is not only important for academic success but also for real-world applications where logical reasoning and numerical proficiency are key.
Advanced Problem Solving Techniques in Mathematics
In mathematics, mastering complex problem-solving methods is essential for tackling higher-level equations and models. This section explores key strategies that can help improve your approach to challenging mathematical scenarios. By applying the right steps and techniques, you can navigate through difficult tasks with clarity and efficiency.
As you progress through various exercises, the key to success lies in understanding the underlying principles and consistently applying learned strategies. Whether you are solving algebraic expressions, working with graphs, or manipulating equations, recognizing patterns and using systematic approaches will lead to more accurate results.
Effective Strategies for Mathematical Challenges
When addressing complex equations, it’s crucial to break down the problem into manageable steps. Identify the core components of the equation and use known methods to simplify each part. Additionally, staying organized and methodical can help reduce errors and ensure that every aspect of the problem is addressed systematically.
Applying Mathematical Concepts in Real-World Problems
Mathematical principles are not just theoretical–they have practical applications in various fields such as engineering, economics, and technology. By honing your problem-solving techniques, you can translate abstract concepts into tangible solutions that solve real-world challenges effectively. This skill set is invaluable in both academic and professional contexts.
Understanding Special Functions in Math
Mathematical operations often involve a variety of expressions and techniques, each suited to solving specific types of problems. In this section, we explore key mathematical concepts that form the backbone of many problem-solving strategies. A solid understanding of these methods is essential for addressing complex equations and developing a deeper grasp of the subject.
By studying these principles, learners gain the ability to approach problems from multiple angles, applying the most effective strategies based on the nature of the task at hand. Each technique is designed to simplify complicated expressions and lead to precise solutions, making them indispensable tools in higher-level mathematics.
| Concept | Description | Example |
|---|---|---|
| Exponential Functions | Functions where the variable is in the exponent | f(x) = e^x |
| Logarithmic Functions | Inverse of exponential functions | f(x) = log(x) |
| Trigonometric Functions | Functions related to angles and periodic motion | f(x) = sin(x), cos(x) |
Common Mistakes in Special Functions
When working with advanced mathematical expressions, it’s easy to make errors that can significantly affect the outcome. Many of these mistakes arise from misinterpreting key concepts or overlooking important details during problem-solving. Understanding where these errors occur can help you avoid them and improve your overall accuracy.
Below are some common mistakes to watch out for when dealing with complex mathematical operations:
- Incorrect application of rules: Many problems require the use of specific rules for solving equations, such as logarithmic properties or trigonometric identities. Misapplying these rules often leads to incorrect results.
- Overlooking domain restrictions: Certain operations, such as division by zero or taking the logarithm of a negative number, are undefined. Ignoring these restrictions can result in mathematical errors.
- Failure to simplify expressions: Complex expressions should often be simplified before attempting to solve them. Failing to reduce terms early on can make solving the problem unnecessarily difficult.
- Sign errors: Mistakes in handling negative signs, especially in exponents or within parentheses, are common and can completely change the result of an operation.
- Misunderstanding the inverse relationship: The inverse operations, such as the relationship between exponential and logarithmic functions, are often misunderstood, leading to incorrect transformations.
By being aware of these frequent mistakes, you can take steps to avoid them and improve your problem-solving efficiency. Practice and careful attention to detail are key to mastering complex mathematical operations.
How to Approach Skills Practice

Mastering complex mathematical concepts requires a structured approach to solving problems. By following a clear, methodical process, you can improve your understanding and accuracy, leading to better results. Here’s a guide to help you tackle challenging exercises effectively.
The key to success is breaking down the problem into manageable steps. This allows you to focus on each part individually and reduces the likelihood of errors. Below are strategies for a more effective approach:
- Understand the Problem: Carefully read the question to identify what is being asked. Clarifying the problem will help you determine which techniques to apply.
- Break Down Complex Equations: Large equations can be intimidating. Start by simplifying them into smaller parts. Focus on one element at a time to make the overall task less overwhelming.
- Identify Key Relationships: Look for patterns or connections between different components of the problem. These insights can often lead to quicker and more accurate solutions.
- Practice with Variety: Working on a wide range of problems helps strengthen your problem-solving abilities. Aim to challenge yourself with problems of increasing difficulty to build confidence.
- Review and Reflect: After solving a problem, review your solution and check for any possible mistakes. Reflecting on your approach will help reinforce concepts and improve future performance.
By following these steps and maintaining a focused mindset, you can approach even the most difficult problems with confidence and clarity. The more you practice with intent, the more proficient you will become at handling advanced challenges.
Tips for Solving Function Problems
When tackling mathematical problems that involve relationships between variables, having a clear strategy is essential. By focusing on key principles and following a systematic approach, you can make complex tasks more manageable and reduce the likelihood of errors. Here are some useful tips to improve your problem-solving skills:
Approach these problems by understanding the core concepts first, then applying the appropriate methods in a logical order. With careful practice and attention to detail, you can efficiently solve even the most challenging equations.
| Tip | Explanation | Example |
|---|---|---|
| Start with Simplification | Break down the equation into simpler parts to make the problem more manageable. | f(x) = (2x + 4) / 2 simplifies to f(x) = x + 2. |
| Identify Patterns | Look for repeated structures or relationships that can guide your solution process. | Recognizing symmetry in a graph can simplify calculations. |
| Use Graphing for Visualization | Plotting the equation can provide insight into its behavior and help identify solutions more easily. | Graphing y = 2x + 3 shows the slope and intercept clearly. |
| Check for Domain Restrictions | Ensure that the values you are working with are within the valid domain of the equation. | A logarithmic equation is only valid for positive numbers. |
By following these tips and applying them to your problem-solving routine, you’ll be able to approach even the most intricate problems with greater clarity and accuracy.
Mastering Mathematical Function Techniques
To excel in advanced mathematical problem-solving, it’s essential to develop a strong command of various techniques used to analyze and manipulate equations. These techniques allow you to simplify complex expressions and find solutions efficiently. Mastery in this area not only enhances your problem-solving skills but also builds a deeper understanding of mathematical relationships and operations.
In this section, we explore some of the key methods that will help you tackle challenging problems. By applying these strategies correctly, you can significantly improve both your accuracy and confidence when solving complex equations.
Key Techniques for Effective Problem Solving
- Factoring: This method is useful for breaking down complex expressions into simpler components. By factoring, you can identify common factors and reduce the complexity of the equation.
- Substitution: Substituting variables allows you to simplify equations and solve for unknowns step by step. This technique is often used to replace complicated terms with simpler ones.
- Graphing: Visualizing equations can help identify solutions more easily. By plotting graphs, you can observe patterns, intersections, and behavior, leading to quicker problem-solving.
- Using Inverses: Recognizing the inverse relationships between operations, such as the inverse of addition (subtraction) or multiplication (division), can simplify many tasks.
Applying These Techniques in Real Problems
Each of these techniques can be applied in different mathematical scenarios. For example, factoring can be particularly useful when dealing with polynomial equations, while substitution is key when solving systems of equations. By practicing these methods, you’ll gain the ability to handle increasingly difficult problems with greater ease.
With consistent practice and a focus on these core techniques, you’ll be well on your way to mastering advanced mathematical concepts and solving problems with precision.
Key Concepts for Special Functions
Understanding advanced mathematical expressions requires a solid grasp of key principles that govern their behavior. These fundamental concepts are the building blocks that help simplify complex operations and allow for the effective manipulation of variables. A deep understanding of these core ideas is essential for solving a wide range of problems accurately and efficiently.
In this section, we will explore several important concepts that are central to working with intricate mathematical relationships. These concepts serve as tools for better comprehension and application of various techniques, making it easier to navigate through more challenging mathematical tasks.
- Domain and Range: The domain refers to the set of all possible input values, while the range defines the set of output values. Understanding these limits helps in determining the validity of operations.
- Inverse Relationships: In many mathematical expressions, certain operations are the inverse of others. Recognizing these relationships allows for easier manipulation and solution finding.
- Continuity: Continuity ensures that a function behaves smoothly without abrupt changes. It’s important to check for discontinuities when solving equations to avoid invalid results.
- Asymptotes: These are lines that a graph approaches but never touches. Understanding asymptotic behavior is crucial for analyzing the long-term trends of an equation.
- Symmetry: Many equations exhibit symmetry, either about the x-axis, y-axis, or the origin. Recognizing symmetry can simplify the problem-solving process by reducing the number of calculations needed.
By internalizing these core concepts, you will be better equipped to understand and manipulate complex mathematical relationships with precision and ease. They are fundamental tools that will support your problem-solving journey in higher mathematics.
Breaking Down Complex Function Problems
When faced with intricate mathematical problems, it’s important to approach them in a structured and systematic way. By deconstructing the problem into smaller, more manageable parts, you can tackle each component one step at a time. This strategy not only makes solving complex equations easier but also improves your overall problem-solving abilities.
The process involves recognizing patterns, simplifying expressions, and identifying relationships between different variables. By taking a methodical approach, you can uncover solutions more efficiently and with greater accuracy.
- Identify Key Variables: The first step is to determine the key variables and constants in the equation. This allows you to focus on what needs to be solved and avoid distractions from irrelevant details.
- Simplify Expressions: Complex expressions can often be reduced into simpler forms. Start by factoring, combining like terms, or simplifying fractions to make the problem easier to handle.
- Work in Stages: Break the problem into smaller, logical steps. Solve one part, then move on to the next. This method prevents errors and keeps the process clear and focused.
- Look for Patterns or Symmetry: Many equations exhibit repeating patterns or symmetrical properties. Recognizing these can save time and lead to faster solutions.
- Use Substitution: If the equation is too complicated, try substituting simpler terms for complex expressions. This can make the problem more approachable and easier to solve.
By following these strategies and maintaining a step-by-step approach, you can break down even the most complex problems into manageable tasks, ultimately leading to more successful solutions.
Why Special Functions Matter in Math
In mathematics, certain types of equations and relationships are pivotal for solving a wide range of problems. These particular forms of relationships often arise in various fields such as physics, engineering, and economics, where they help describe complex systems. Understanding and applying these key expressions is crucial for advancing in mathematical studies and solving real-world problems effectively.
These mathematical models are not just theoretical; they have practical applications that can simplify the process of analyzing data, predicting outcomes, and solving problems in diverse areas of study. Without a solid understanding of these core relationships, it would be much harder to tackle the advanced challenges that arise in science and technology.
Mastering these techniques provides the tools necessary to approach a variety of mathematical challenges with confidence. Whether dealing with theoretical calculations or real-world applications, these concepts form the foundation of much of modern mathematics and help to drive innovation and understanding in many scientific disciplines.
Strategies for Improved Function Practice
Enhancing your ability to solve complex mathematical problems requires consistent effort and effective strategies. By adopting targeted approaches, you can streamline your learning process and improve your problem-solving skills. These strategies will help you build a strong foundation and tackle even the most challenging equations with confidence.
Here are several approaches to improve your ability to handle mathematical expressions and equations:
- Understand the Basics: Start by mastering the fundamental concepts that underpin advanced problems. A solid grasp of the basics will help you recognize patterns and simplify more complex tasks.
- Break Down Problems: Deconstruct problems into smaller, manageable parts. This allows you to focus on one element at a time and reduces the complexity of the overall task.
- Practice Regularly: Consistent practice is key to mastery. The more you engage with problems, the more familiar you become with different techniques and methods.
- Work on Real-Life Applications: Apply what you’ve learned to practical problems. This helps solidify your understanding and shows the real-world relevance of abstract concepts.
- Review Mistakes: Analyzing errors can be a powerful learning tool. By understanding where you went wrong, you can refine your approach and avoid similar mistakes in the future.
- Seek Help When Needed: Don’t hesitate to reach out to peers, instructors, or online resources. Sometimes, a different perspective can provide clarity and new insights.
By incorporating these strategies into your study routine, you will gradually develop a deeper understanding and greater proficiency in solving complex mathematical problems.
Examples of Special Functions in Use
Mathematical relationships play a crucial role in a wide range of practical applications. Understanding how these expressions are applied in real-world scenarios can provide insight into their significance and utility. From engineering to economics, these mathematical tools are essential for modeling complex systems, making predictions, and solving diverse problems.
In this section, we will explore various examples of how these key relationships are used in different fields. These examples will illustrate their practical value and demonstrate how mastering these concepts can enhance your problem-solving capabilities.
Application in Engineering
In engineering, certain mathematical relationships are used to model physical systems, such as electrical circuits, fluid dynamics, and structural integrity. For example, in electrical engineering, equations that describe the behavior of circuits involving resistors, capacitors, and inductors often rely on specific forms of mathematical expressions. By understanding these relationships, engineers can design more efficient systems and predict their behavior under different conditions.
Application in Economics
In economics, these mathematical models are used to forecast trends, such as inflation rates, supply and demand, and market equilibrium. These relationships help economists analyze the impact of various variables on the economy, providing valuable insights for policy-making and business strategy. For instance, supply and demand curves can be analyzed using certain mathematical techniques to predict price fluctuations and market behavior.
| Field | Example | Purpose |
|---|---|---|
| Engineering | Ohm’s Law | To model the relationship between voltage, current, and resistance in electrical circuits. |
| Economics | Supply and Demand Curves | To forecast price fluctuations and understand market behavior. |
| Physics | Newton’s Laws of Motion | To describe the movement of objects and the forces acting upon them. |
These examples highlight the importance of mathematical expressions in solving real-world challenges. Mastery of these concepts not only enhances theoretical understanding but also prepares individuals to apply their knowledge in practical settings effectively.
Common Function Types You Should Know
Understanding the different types of mathematical expressions is crucial for solving a wide range of problems. Each type of relationship serves a specific purpose and is used in various fields, from basic arithmetic to complex scientific calculations. Familiarity with these key forms allows for a deeper understanding and more effective problem-solving techniques.
Below are some of the most common types of mathematical expressions that are essential to know:
- Linear Relationships: These describe constant rates of change and are represented by straight lines. The simplest form is y = mx + b, where m is the slope and b is the y-intercept. These are used in a wide range of applications, from economics to physics.
- Quadratic Expressions: These are used to describe parabolic curves and take the form y = ax^2 + bx + c. Quadratic relationships are often used in physics, especially in projectile motion, and are also critical in optimization problems.
- Exponential Functions: These express growth or decay at a constant rate, such as y = a * e^(bx). Exponential relationships are widely used in fields like biology (population growth), finance (compound interest), and physics (radioactive decay).
- Logarithmic Functions: The inverse of exponential functions, logarithmic expressions help solve equations involving exponential growth or decay. They are commonly written as y = log_b(x), and are fundamental in solving equations related to sound intensity and pH levels in chemistry.
- Trigonometric Functions: These relationships involve angles and ratios in right-angled triangles, expressed as sin(x), cos(x), tan(x), and are crucial in fields like engineering, physics, and navigation.
These are just a few examples of the types of expressions you’ll encounter in mathematics. Understanding these forms and their properties not only improves your ability to solve specific problems but also enhances your overall mathematical thinking and analytical skills.
Step-by-Step Guide to Solving Functions
Solving mathematical expressions involves understanding their structure and applying systematic steps to find the correct solutions. By following a methodical approach, you can break down even complex problems into manageable parts. This guide outlines a straightforward process for tackling these challenges effectively and efficiently.
Here’s a step-by-step method to help you approach and solve mathematical relationships:
- Identify the given information: Carefully examine the problem and note down all the known values. These could include variables, constants, or coefficients that are directly provided in the equation.
- Understand the relationship: Determine the type of relationship involved. Whether it’s linear, quadratic, or exponential, recognizing the form of the equation helps in selecting the right method for solving.
- Simplify the equation: Combine like terms and move all variables to one side of the equation. If the equation is too complex, try to factor or expand terms to make it easier to work with.
- Apply the appropriate method: Depending on the equation type, use the relevant solving technique. For linear equations, this might involve simple algebraic manipulation, while for quadratic equations, factoring or the quadratic formula may be necessary.
- Solve for the unknowns: Once the equation is simplified, solve for the variable. Be mindful of multiple possible solutions, especially in non-linear problems where more than one answer may exist.
- Check your solution: After solving, substitute your answer back into the original equation to verify its correctness. This helps ensure that no mistakes were made during the solving process.
By following these steps, you can approach even the most challenging mathematical expressions with confidence, ensuring you arrive at accurate solutions each time.
Best Resources for Function Practice
Mastering mathematical relationships requires consistent exposure to a variety of problems. The best way to improve is by engaging with resources that provide a wide range of challenges, explanations, and step-by-step solutions. Below are some excellent tools and platforms to help you sharpen your understanding and enhance your problem-solving abilities.
Online Platforms
Websites like Khan Academy, Coursera, and edX offer in-depth courses with video tutorials and exercises to help reinforce key concepts. These platforms often provide interactive features that allow you to test your understanding as you progress through lessons.
Textbooks and Practice Books
Books dedicated to algebra, calculus, or advanced mathematics often contain extensive practice problems, complete with answers and explanations. Popular options include “Precalculus” by James Stewart and “Calculus” by Ron Larson, which cover a wide array of topics and provide valuable insights for learners at all levels.
By utilizing these resources, you’ll be able to systematically build your proficiency and approach even the most complex problems with confidence.
Understanding Function Notation in Math
Mathematical notation plays a critical role in conveying complex ideas with simplicity. When dealing with relationships between variables, the symbols used are essential for communicating the operations being performed. Function notation is one such system that provides a structured way to represent how one quantity depends on another.
In function notation, we commonly express a relationship as f(x), where f represents the name of the function and x is the input value. This notation allows us to easily evaluate expressions by substituting values for the variable and calculating the corresponding output. Understanding this system is crucial for solving equations and grasping advanced concepts in mathematics.
Advanced Tips for Function Problem Solving
Solving complex mathematical problems requires more than just understanding basic concepts; it involves applying advanced strategies that simplify the process and enhance accuracy. By mastering these techniques, you can approach even the most challenging problems with confidence and efficiency.
One effective method is to break down the problem into smaller, manageable parts. This allows you to focus on individual components without feeling overwhelmed. Additionally, recognizing patterns in the equations or graphs can lead to quicker solutions, as many problems share similar structures. It’s also helpful to revisit foundational principles and ensure that each step is logically sound before proceeding to the next. By building on these advanced strategies, you’ll develop a deeper understanding and improve your problem-solving skills.
How to Check Your Function Answers
After solving a mathematical problem, it’s crucial to verify that your results are correct. Checking your work not only helps ensure accuracy but also strengthens your understanding of the underlying concepts. This process allows you to identify any mistakes early on, improving both your confidence and problem-solving skills.
Double-Check Your Steps
The first step in verifying your solution is to review each step of your work. Go through the calculations carefully and ensure that all operations were performed correctly. Even small errors can lead to incorrect results, so it’s important to check for any overlooked mistakes or miscalculations. By retracing your steps, you can identify where things may have gone wrong and correct them.
Use Alternative Methods
Another effective way to check your results is by using a different approach to solve the same problem. For example, if you used algebraic manipulation to find your answer, try graphing the equation or using a numerical method to verify your solution. If both methods yield the same result, it’s a strong indication that your solution is correct. Additionally, you can use online calculators or tools to cross-check your findings, though it’s important to understand the reasoning behind the solution to avoid relying solely on technology.