
Preparation for any challenging math assessment requires understanding the core principles and honing problem-solving skills. By revisiting sample questions and analyzing detailed solutions, students can deepen their knowledge and boost their confidence. This process involves not just memorization, but also the development of strategies for tackling complex problems efficiently.
When reviewing previous test papers, it’s crucial to focus on both the format and the underlying concepts. Knowing how to approach each type of question helps streamline the preparation process, ensuring that you can apply your knowledge effectively under timed conditions. Additionally, breaking down each problem step-by-step allows for a clearer understanding of the methods involved.
In this guide, we explore how to make the most of previous assessment materials, offering insight into key concepts, techniques, and common pitfalls. Whether you’re preparing for a final test or looking to improve your mathematical reasoning, this approach will help sharpen your skills and enhance your performance on similar challenges.
2008 AP Calculus AB Practice Exam Answers

Reviewing past assessment materials can be a powerful tool for reinforcing key mathematical concepts. By examining solutions to complex problems, students can gain a better understanding of the methods used to solve them and identify common challenges faced during testing. This section will focus on how analyzing sample questions from previous years can improve performance on future assessments.
Each question offers an opportunity to explore different strategies for problem-solving. By studying how answers are derived step-by-step, you can learn to approach similar questions more efficiently. Understanding the rationale behind each solution is crucial for mastering advanced topics and applying techniques correctly under timed conditions.
In this section, we break down several typical problems and their solutions to provide clear guidance on how to handle various question types. Whether tackling theoretical problems or more practical scenarios, this approach will help solidify your comprehension and build confidence in your abilities.
Key Topics Covered in the Exam
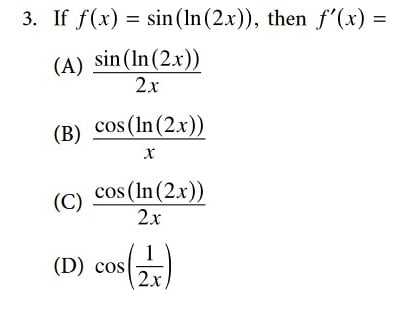
Understanding the core areas of focus in any advanced assessment is essential for targeted preparation. Certain mathematical concepts are frequently tested, and a solid grasp of these topics can significantly improve performance. This section highlights the key subjects that are commonly addressed, helping you prioritize your study efforts and build a well-rounded skill set.
Functions and Their Properties
A deep understanding of functions, their behavior, and how they are manipulated forms the foundation of most questions. Topics such as limits, continuity, and transformations are critical. Knowing how to analyze and interpret different types of functions, from linear to exponential, is key to tackling more complex problems.
Integration and Differentiation Techniques
The ability to apply differentiation and integration methods is central to success in higher-level mathematics. Familiarity with the rules of derivatives, the chain rule, and integration by parts is vital. These concepts form the core of many problems, requiring both theoretical knowledge and practical application skills.
How to Approach AP Calculus Problems
Success in higher-level mathematics assessments relies on developing a strategic approach to problem-solving. Rather than memorizing isolated formulas or methods, it’s essential to understand the concepts at the core of each question. By focusing on breaking down problems systematically and applying logical steps, you can improve accuracy and efficiency under time constraints.
Understanding the Problem
The first step in tackling any challenging problem is to carefully read and analyze it. Pay attention to key details, such as given information, what is being asked, and any specific conditions or constraints. Identifying the problem type early on allows you to choose the appropriate method for solving it, whether it’s solving for an unknown variable or finding an integral.
Applying the Right Techniques
Once you’ve grasped the problem, select the most effective technique for solving it. Whether you need to differentiate, integrate, or apply rules of limits, choose the method that best fits the scenario. Practice is crucial in recognizing which technique works best for various types of questions and understanding when to apply it accurately.
Step-by-Step Solutions for Exam Questions

Breaking down complex problems into manageable steps is a key strategy for success in any challenging test. By following a structured approach to each question, you can ensure that you don’t overlook any crucial details and solve the problem efficiently. This method not only helps to achieve the correct solution but also enhances understanding of the concepts being tested.
Each problem can be tackled by identifying the underlying principles and applying the right techniques progressively. Start by reading the question carefully, then move through the necessary steps one at a time, ensuring you follow logical reasoning. By doing so, you’ll avoid making common mistakes and build confidence in solving similar questions in the future.
In the sections that follow, we’ll demonstrate this step-by-step approach by working through several sample problems. For each, we’ll break down the solution process to highlight the key concepts and methods involved, helping you learn how to approach similar questions with ease.
Tips for Solving Multiple Choice Questions
Multiple-choice questions often test both your knowledge and your ability to quickly analyze different options. Success in these types of questions requires a clear understanding of the concepts and a strategic approach to eliminate incorrect answers. By applying a few key techniques, you can increase your chances of selecting the correct answer, even if you’re unsure at first.
Read Each Question Carefully
Before jumping to the answer choices, take a moment to fully read and comprehend the question. Pay attention to every detail and ensure you understand exactly what is being asked. If the question involves a calculation, try to identify the necessary formulas or concepts before looking at the options.
Eliminate Clearly Wrong Choices
Start by eliminating any answers that are obviously incorrect. Often, there are one or two options that are clearly not suitable based on your knowledge of the subject. Narrowing down the choices early on increases your chances of selecting the correct answer even if you’re unsure about the remaining options.
| Step | Action |
|---|---|
| 1 | Read the question carefully. |
| 2 | Identify key terms and concepts. |
| 3 | Eliminate clearly wrong answers. |
| 4 | Use the process of elimination. |
By following these simple steps, you can significantly improve your accuracy in multiple-choice questions and better manage your time during the assessment.
Strategies for the Free Response Section
The free response section is often the most challenging part of any test, requiring you to show a deep understanding of the material and demonstrate your problem-solving skills. Unlike multiple-choice questions, these problems demand clear, logical reasoning and the ability to present your work step by step. Developing a strong approach to this section can greatly improve your performance and ensure that you cover all aspects of each question.
Plan Your Time Carefully
Effective time management is crucial when tackling open-ended questions. Allocate enough time for each problem, but be sure not to spend too long on any one question. If you find yourself stuck, move on to the next problem and return to the difficult one later. This approach ensures that you have enough time to answer all questions thoroughly.
Show All Work and Explain Your Reasoning
One of the most important aspects of the free response section is clearly showing your work. Even if you arrive at the correct solution, you may lose points if you don’t demonstrate the steps you took to get there. Make sure to explain your reasoning, as this shows your understanding of the concepts and makes it easier to earn partial credit if a mistake is made.
| Step | Action |
|---|---|
| 1 | Read each problem carefully and highlight key information. |
| 2 | Break the problem into manageable steps. |
| 3 | Work through each part methodically and check your work. |
| 4 | Write clear, concise explanations of your reasoning. |
By following these strategies, you can approach the free response section with confidence, ensuring that you showcase your full understanding and earn maximum points for each problem.
Common Mistakes to Avoid on the Exam
Even the most prepared students can make mistakes during an assessment, especially under pressure. It’s crucial to be aware of common errors so you can take steps to avoid them. By recognizing potential pitfalls, you can focus on maintaining accuracy and ensuring that you approach each question with confidence and clarity.
One frequent mistake is rushing through the problems without fully understanding what’s being asked. It’s essential to read each question carefully and identify key information before attempting a solution. Skipping this step can lead to misinterpretation of the question and unnecessary errors.
Another common issue is neglecting to show all steps or explain reasoning. While it might seem like a time-saver, skipping work can result in losing valuable points, even if the final answer is correct. Always provide a clear, logical explanation for your methods and show your work in detail to demonstrate your understanding.
Lastly, failing to review your work is a significant error. In the rush to finish, many overlook small mistakes that could have been easily corrected with a quick review. Make sure to allocate time at the end to check your answers and ensure that all steps are accurate and clearly presented.
Understanding Concepts Through Practice
Mastering advanced mathematical concepts requires more than just memorization of formulas; it demands a deep understanding of the principles behind the methods. One of the most effective ways to solidify this knowledge is through continuous application. Working through various problems helps you gain a practical understanding of how concepts are used and allows you to see how theory translates into real-world problem solving.
Building a Strong Foundation
To truly grasp the subject, it’s important to first establish a solid foundation in the fundamental principles. This involves understanding the key concepts in depth, such as rates of change and area calculations, and how they connect with each other. By practicing these core concepts regularly, you strengthen your ability to approach more complex problems with ease.
Improving Problem-Solving Skills
As you encounter different types of problems, you learn to recognize patterns and develop strategies for solving them. Regular practice challenges you to think critically and apply your knowledge in new ways, helping you refine your problem-solving techniques. The more you practice, the more intuitive your understanding becomes, allowing you to solve even the toughest problems with confidence.
How to Maximize Your Score
Achieving a high score on any challenging test requires a combination of preparation, strategy, and effective time management. It’s not just about knowing the material–it’s about applying the knowledge efficiently and confidently under timed conditions. By focusing on key areas and approaching the test strategically, you can maximize your performance and increase your chances of success.
First and foremost, consistent practice is essential. Familiarizing yourself with the types of questions and understanding the concepts thoroughly will give you the edge you need. The more you practice, the more comfortable you become with the format and style of the problems, allowing you to respond more quickly and accurately when it counts.
Additionally, time management is a critical skill. Be sure to allocate enough time for each section, and don’t get bogged down on any single question. If you find yourself stuck, move on and come back later. Prioritize the questions you are most confident in, and ensure you leave time to double-check your work for potential errors.
Lastly, remember to stay calm and focused during the test. Stress can undermine your performance, so approach each problem with a clear mind and a systematic approach. By remaining composed, you’re more likely to recall information accurately and apply the correct techniques to solve each question effectively.
Reviewing Core Formulas
To perform well on any advanced math test, it is essential to have a strong command over the key formulas that form the foundation of problem-solving techniques. These formulas are not only tools for solving specific problems but also serve as shortcuts that help streamline the thought process. Having them memorized and understanding when and how to apply them can significantly improve efficiency and accuracy during the test.
Essential Formula Categories
There are several key categories of formulas that are critical for success in any mathematical assessment. These categories cover the core areas that often appear in test questions, including differentiation, integration, and limits. A thorough understanding of these areas ensures you are ready for any question type that may arise.
- Limits: The basic limit rules, L’Hopital’s Rule, and special limits for trigonometric and exponential functions.
- Derivatives: Power rule, product and quotient rules, chain rule, and derivatives of common functions (polynomials, logarithms, etc.).
- Integrals: Fundamental theorem of calculus, integration by parts, substitution, and common integrals of trigonometric and exponential functions.
Key Formulas to Memorize
While understanding concepts is important, memorizing the most frequently used formulas will save time during the test and help avoid mistakes. Here are some of the most critical formulas you should commit to memory:
- Power Rule: If f(x) = x^n, then f'(x) = n * x^(n-1).
- Product Rule: If f(x) = u(x) * v(x), then f'(x) = u'(x) * v(x) + u(x) * v'(x).
- Chain Rule: If f(x) = g(h(x)), then f'(x) = g'(h(x)) * h'(x).
- Integration by Parts: ∫ u dv = uv – ∫ v du.
By regularly reviewing these core formulas and practicing their application, you can develop a more intuitive understanding and gain confidence in your ability to tackle a wide range of problems. Keep a formula sheet handy during your study sessions to reinforce your memory, and apply these formulas to various types of problems to ensure you are ready for the test.
AP Exam Scoring Breakdown
Understanding the scoring system is crucial for maximizing your performance and setting realistic goals. The scoring process for advanced placement assessments involves both multiple-choice questions and free-response sections, each contributing a specific weight to the overall score. Familiarizing yourself with how each section is graded can help you prioritize your time and effort during the test.
Multiple-Choice Section
The multiple-choice portion of the test is designed to assess your ability to recognize correct approaches and apply concepts quickly. Each correct answer contributes to your total score, while incorrect answers typically do not carry a penalty. This section is usually the largest in terms of points, so it’s important to pace yourself and attempt every question, even if you’re unsure. When you feel confident, move quickly; when uncertain, eliminate as many options as possible to improve your chances of choosing the right answer.
Free-Response Section

The free-response section evaluates your ability to apply concepts in a more open-ended format. Here, you’ll be required to explain your reasoning, show your work, and arrive at the correct solutions. The free-response answers are graded based on accuracy, clarity, and logical progression. Be sure to show all steps and avoid skipping any part of the process, as partial credit is awarded for correct methodology even if the final answer is incorrect. This section plays a crucial role in your overall score, and effectively communicating your thought process can make a significant difference.
Resources for Additional Practice

To strengthen your understanding and improve your problem-solving skills, it is essential to engage with various resources designed for further practice. These resources offer different formats of questions, explanations, and solutions, which will help you deepen your grasp of key concepts. Regular practice with diverse material will ensure you are well-prepared for any challenge that may arise during assessments.
Online Platforms

Several online platforms provide interactive problems, tutorials, and full practice sets that are invaluable for reinforcement. Here are some recommended websites:
- Khan Academy: Offers detailed lessons and exercises covering a wide range of topics, perfect for guided learning and self-paced practice.
- AP Classroom: This official resource by College Board offers various resources, including past questions and personalized feedback based on your progress.
- PatrickJMT: Features short video lessons explaining step-by-step solutions to complex problems and mathematical concepts.
Books and Study Guides
Books remain an excellent source of structured learning. Consider these highly recommended study guides:
- Barron’s AP Study Guide: A comprehensive guide with practice questions, detailed solutions, and test-taking strategies.
- 5 Steps to a 5: Known for its structured approach, this series offers practice problems, model responses, and valuable tips for students looking to boost their score.
- Cracking the AP Series by Princeton Review: Includes full-length practice tests, answer keys, and in-depth explanations.
Incorporating these resources into your study routine will not only enhance your comprehension but also provide you with the variety of challenges necessary to refine your skills and gain confidence for the upcoming tests.
How to Use the 2008 Exam for Preparation
Using past assessment papers as a study tool can be highly beneficial in reinforcing your knowledge and improving your test-taking strategies. By working through older tests, you can familiarize yourself with the structure of questions, the types of topics commonly covered, and the level of difficulty you may encounter. This will help you build confidence and identify areas that require more attention.
Start by reviewing the problems in their entirety, without initially looking at the provided solutions. This will allow you to test your own understanding and simulate the test-taking experience. Focus on time management, and try to complete each section within the recommended time frame. Afterward, thoroughly analyze your work and compare it with the official solutions, paying close attention to any mistakes and understanding the correct methods for solving the problems.
In addition to simply solving the problems, use the past test as a diagnostic tool. Identify patterns in the types of problems you struggle with most and dedicate more study time to those specific areas. Additionally, consider reviewing any related concepts that are crucial for mastering those problem types. By using the past assessment in this way, you’ll gain valuable insights into your strengths and weaknesses, guiding your preparation for future assessments.
Analyzing Past Exam Trends
Reviewing previous assessments allows students to identify recurring themes and problem formats. By analyzing the patterns in past tests, you can pinpoint the areas that are most frequently tested, enabling you to focus your efforts on mastering those specific topics. Understanding these trends also helps you anticipate the types of questions that might appear in future assessments, making your preparation more targeted and efficient.
Identifying Commonly Tested Topics
One of the first steps in analyzing past assessments is recognizing which topics consistently appear in each test. For example, certain mathematical concepts or problem types may recur regularly, signaling their importance in the curriculum. Make note of these frequently tested areas and dedicate additional study time to mastering them.
- Limits and Continuity
- Derivatives and Their Applications
- Integrals and Antiderivatives
Understanding Question Formats and Difficulty
Another critical aspect to consider when reviewing past tests is the format and difficulty level of the questions. Some problems may follow a predictable structure, while others may require deeper reasoning or multi-step problem-solving. Familiarizing yourself with these question formats helps you better manage your time and approach during the actual test. It also allows you to assess which types of questions tend to be more challenging, so you can prepare accordingly.
Importance of Time Management During the Exam
Effective time management is crucial for success in any timed assessment. The ability to allocate your time wisely can determine how well you perform under pressure. Without a clear plan, students may find themselves rushing through questions or, conversely, spending too much time on one section and not completing others. By practicing time management, you ensure that you can tackle each question with the attention it requires, maximizing your potential score.
Strategies for Managing Your Time

Here are a few strategies to help manage your time effectively during the test:
- Set Time Limits for Each Section: Before starting, familiarize yourself with the total time allotted and divide it among the different parts of the test. Make sure to stick to these time limits to ensure you have enough time for all sections.
- Prioritize Easy Questions: Start with the questions that you find easiest or are most confident about. This will help you build momentum and ensure that you secure those points early on.
- Don’t Get Stuck: If a question is taking too long, move on to the next one and come back to it later. Avoid spending too much time on a single problem, especially if it’s difficult.
Practice with Time Constraints
One of the best ways to improve your time management skills is to simulate test conditions during your study sessions. Practice solving problems within the time limits to get a sense of how long each question takes. This will help you develop a more accurate sense of timing and boost your confidence during the actual test.
How to Stay Calm Under Pressure
Staying composed under stressful circumstances is key to performing well in any high-pressure situation. When facing a timed assessment or a challenging task, feelings of anxiety or panic can easily disrupt your focus and hinder your ability to think clearly. By learning how to manage these emotions, you can maintain a steady mindset, think more clearly, and approach the task with confidence.
Techniques for Staying Calm
Here are a few strategies to help you remain calm when the pressure is on:
- Practice Deep Breathing: Slow, deep breaths can help calm your nervous system and reduce feelings of panic. Try inhaling for a count of four, holding for four, and exhaling for four to help regulate your breathing and regain control.
- Take Regular Breaks: During study sessions or when working on a difficult problem, take short breaks to clear your mind. Even a brief pause can help reduce stress and refocus your attention.
- Positive Visualization: Imagine yourself successfully completing the task at hand. Visualization can help boost your confidence and reduce anxiety about potential outcomes.
- Stay Present: Focus on the present moment rather than worrying about the future or past mistakes. Concentrating on one question at a time can help reduce feelings of overwhelm.
Preparation is Key
Being well-prepared for any assessment or challenge is one of the best ways to stay calm. The more familiar you are with the material or the format of the task, the less likely you are to feel anxious when the time comes to perform. Consistent practice and preparation help you feel more confident and in control when it matters most.