
Preparing for high-level mathematics assessments requires a solid understanding of key principles and the ability to apply them under time pressure. One effective approach is to work through previous test materials, which offer a glimpse into the types of challenges you might encounter. By studying and analyzing solutions to past questions, you can sharpen your skills and improve problem-solving efficiency.
Building confidence in mathematical reasoning comes from recognizing common patterns and understanding the methods used to solve complex problems. Focusing on the areas that tend to be most challenging will help refine your techniques and give you a better grasp of the subject matter. Through careful review and practice, you can improve both speed and accuracy when tackling similar problems in the future.
In this section, we will break down typical problems from past assessments and explore the correct methods for tackling them. The goal is to provide a structured way to approach each type of question, helping you gain the confidence needed to perform well in any similar future test situation.
2012 AP Calculus AB Exam Overview
The advanced mathematics test assesses a student’s understanding of key concepts and problem-solving techniques. This assessment is designed to challenge participants with a series of thought-provoking questions that test both theoretical knowledge and practical application skills. It is split into two sections: one focused on multiple-choice questions and the other on free-response questions, providing a comprehensive evaluation of the subject matter.
Each section targets different areas of mathematical proficiency:
- Multiple-choice questions: These questions test your ability to quickly apply mathematical concepts and select the most accurate solution from a set of options.
- Free-response questions: Here, you must demonstrate your reasoning and calculation steps while solving more complex problems, often requiring multiple stages of work.
The assessment covers a range of topics, including but not limited to:
- Functions and their properties
- Rates of change and limits
- Integration and differentiation techniques
- Applications of integrals and derivatives in real-world scenarios
- Solving differential equations and analyzing solutions
By working through previous materials and studying the structure of past assessments, students can identify the areas that may require more attention and focus. Each problem has its unique approach, which allows for a deeper understanding of the overall subject. Preparation for this type of test involves not only mastering the content but also becoming comfortable with the format and pacing of the assessment.
Understanding the AP Calculus AB Exam Format
The assessment consists of two main components: a multiple-choice section and a free-response section. Both parts are designed to test a student’s proficiency in solving advanced mathematical problems and applying learned concepts in different scenarios. The format encourages both speed and accuracy, making it crucial for students to manage their time effectively.
The multiple-choice section includes a series of questions where students must select the correct option based on their understanding of the material. This section is structured to assess quick recall, conceptual understanding, and the ability to apply formulas and techniques to solve problems.
The free-response section requires detailed written solutions, where students demonstrate their problem-solving process and mathematical reasoning. This section often includes multi-step problems that assess a deeper understanding of the material, requiring clear explanations and well-organized calculations.
Both sections are timed, with the multiple-choice part typically being shorter but requiring faster decision-making, while the free-response portion allows for more time to work through each problem in detail. Mastery of both sections is essential to perform well on the assessment.
Key Concepts Tested in 2012 Exam
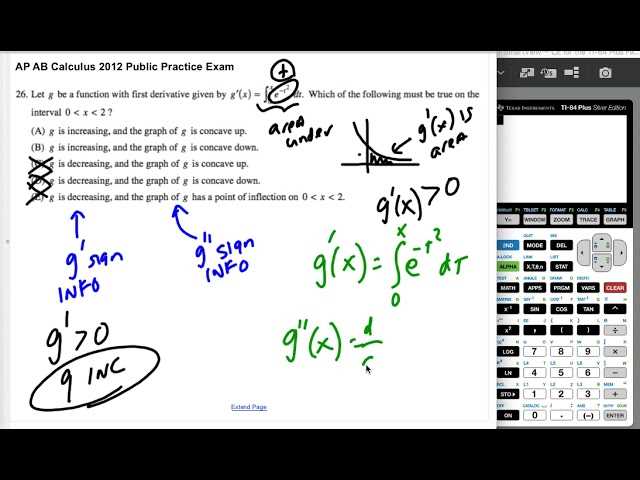
The assessment covers several foundational topics in advanced mathematics, focusing on both theoretical understanding and practical application. Key concepts include functions, rates of change, and the use of different techniques for solving complex problems. Mastery of these topics is essential for achieving a high score.
One major focus is on the understanding of limits and continuity, which are crucial for analyzing the behavior of functions. Additionally, the test assesses the application of derivatives and integrals, particularly in solving real-world problems. These concepts are foundational for understanding how mathematical models are used to represent various physical phenomena.
Other areas covered include the interpretation of graphs, understanding the relationships between functions and their derivatives, and applying integration techniques to find areas and volumes. The assessment also tests problem-solving skills in the context of differential equations and optimization.
How to Use Public Practice Exams
Working through past assessments is an excellent way to familiarize yourself with the format, structure, and types of problems you will encounter in a high-level mathematics test. By engaging with these materials, you can identify key areas that require more focus and refine your problem-solving strategies.
Start by reviewing each problem carefully and try to solve it without referring to any solutions. This will help you practice under realistic conditions and test your understanding of the concepts. Afterward, check your work by reviewing the correct answers and study the solution process to understand any mistakes you may have made.
Additionally, use these resources to time yourself, simulating real test conditions. This will help improve your time management skills and ensure that you can efficiently work through the problems within the allotted time. Focus on the types of questions that challenge you the most and revisit those areas for further practice.
Common Pitfalls in Calculus Exams
During advanced mathematics assessments, students often encounter specific challenges that can lead to mistakes. These common pitfalls can undermine performance, even for those with strong understanding. Being aware of these issues and preparing accordingly can make a significant difference in the final results.
Misinterpreting the problem: One of the most frequent errors is misunderstanding the question or missing key details. Pay close attention to the wording and any conditions or constraints given in the problem. Carefully read each part before attempting a solution.
Skipping steps: Rushing to the final answer without showing intermediate steps is a common issue, especially in the free-response section. It’s essential to clearly outline your reasoning and calculations, not only for clarity but also to ensure you don’t overlook critical stages in the process.
Forgetting units or context: In some problems, especially those involving real-world applications, students may forget to include appropriate units or interpret the results in context. Always double-check that the answers make sense in the context of the problem and include any necessary units or explanations.
Time pressure: The clock can often feel like an adversary during these assessments. Managing your time wisely, pacing yourself, and knowing when to move on from a difficult problem are key strategies to avoid falling into the trap of spending too long on a single question.
Steps to Prepare for AP Calculus
Preparing for an advanced mathematics assessment requires a structured approach, focusing on both understanding the core concepts and mastering problem-solving techniques. A well-planned study strategy can greatly enhance performance and reduce anxiety on test day. Here are some effective steps to help guide your preparation process.
Master Key Concepts

The first step is to ensure you have a solid understanding of the fundamental concepts. Review important topics such as limits, derivatives, and integrals. Focus on mastering each topic one at a time, and make sure to grasp the underlying principles before moving on to more complex problems. Use resources such as textbooks, online lectures, and practice problems to reinforce your understanding.
Practice Problem-Solving
Next, work through as many practice problems as possible. Start with basic exercises to build your confidence and gradually move to more challenging questions. Pay attention to the types of problems that appear most often in past assessments and focus on improving your efficiency in solving them. This will help you become comfortable with the question format and identify areas where you may need more practice.
Finally, test yourself under timed conditions to simulate the actual test environment. This will help you manage your time better during the real assessment and allow you to identify any areas where you might be struggling. Consistent practice and a focus on key concepts will help you achieve the best possible results.
Analyzing the 2012 Exam Questions
Reviewing past test questions is an invaluable tool for understanding the structure and focus of an advanced mathematics assessment. By carefully analyzing the types of problems presented, students can gain insights into the most commonly tested concepts and refine their problem-solving techniques. A deeper look at how questions are framed and what is expected in each solution will help sharpen both knowledge and approach.
Identifying Key Themes: The questions are typically designed to assess specific mathematical principles, such as rates of change, function behavior, and integration techniques. Understanding which themes reappear throughout the assessment allows students to focus their study on the areas that matter most. Recognizing patterns in problem types also aids in predicting the kind of questions to expect in future tests.
Breaking Down Problem Solving Methods: It’s important to not only solve the problems but to understand the reasoning behind each solution. Pay close attention to the steps involved in each question, including any formulas or theorems applied. By breaking down the methodology, you can identify the most efficient approach to solving similar problems in the future. Reviewing solutions will also help in recognizing any mistakes made and understanding how to avoid them in future attempts.
Time management is another crucial aspect: As you analyze the questions, take note of how long each problem might reasonably take to complete. Simulating this timed approach while studying will prepare you to manage your time effectively when working through similar problems in a test setting.
Tips for Answering Multiple Choice Questions

Multiple-choice questions often require quick thinking and a clear understanding of the concepts. While they may seem straightforward, it’s important to approach them strategically to ensure accuracy and efficiency. The following tips will help you improve your performance when facing these types of questions.
Carefully Read Each Question
Before selecting an answer, make sure to read the question thoroughly. Pay close attention to keywords and any specific instructions or conditions mentioned. Often, multiple-choice questions are designed to test not just knowledge but also comprehension and attention to detail.
Eliminate Incorrect Answers First

One effective strategy is to immediately eliminate the clearly incorrect options. This improves your chances of choosing the correct answer, even if you’re unsure. By narrowing down the choices, you increase the likelihood of selecting the right one through logical deduction.
| Incorrect Answer | Why It’s Incorrect |
|---|---|
| Option A | Does not satisfy the given conditions of the problem. |
| Option C | Contradicts a fundamental concept in the problem. |
| Option D | Fails to align with the problem’s numerical constraints. |
After eliminating the obvious wrong answers, you can focus on the remaining choices. If still uncertain, make an educated guess based on the process of elimination and your understanding of the material. Always double-check your answer before finalizing it, as time allows.
Strategies for Solving Free Response Questions

Free response questions require more than just the correct final answer; they demand a clear and logical explanation of your thought process. These questions often assess your ability to demonstrate understanding and apply concepts to solve complex problems. Developing a systematic approach is key to successfully tackling these types of questions.
Here are some strategies to help you effectively solve free response questions:
- Understand the problem: Carefully read the entire question and break it down into smaller, manageable parts. Pay attention to all given information, including any conditions or constraints, to avoid missing important details.
- Organize your work: Clearly write out all steps of your solution. Start with the formula or method you plan to use, and show each intermediate step. A well-organized solution is easier to follow and demonstrates your understanding of the process.
- Explain your reasoning: Don’t just write down calculations–explain why you are using specific techniques or steps. Even if you arrive at the correct answer, a detailed explanation helps clarify your thinking and maximizes the points you can earn.
- Check your work: Before finalizing your answer, review each part of the problem to ensure that your solution is logical and that no mistakes were made. Double-check calculations and verify that your final answer makes sense in the context of the problem.
By following these strategies, you can enhance the clarity of your solutions and demonstrate a thorough understanding of the material, leading to a stronger performance on free response sections.
How to Check Your Calculus Answers
Ensuring the accuracy of your solutions is crucial when working through complex mathematical problems. It’s not enough to simply arrive at an answer; verifying the correctness of your work is essential for both understanding the process and avoiding simple mistakes. Here are several techniques you can use to double-check your solutions and confirm their validity.
- Review the Problem Statement: Re-read the question carefully to make sure you’ve answered exactly what was asked. Sometimes, it’s easy to misinterpret the problem or overlook key information. Ensure that you’ve considered all given variables and conditions before moving forward.
- Check Your Calculations: Go through each step of your solution again. Verify that all calculations are accurate and that you haven’t skipped any steps. Look for any arithmetic or algebraic errors that may have crept in.
- Use a Different Approach: If possible, try solving the problem using a different method or formula. This can help confirm that your initial solution was correct. For example, if you used derivatives in one approach, you could try verifying your result by applying integration or using a graphing method.
- Estimate Your Answer: Check if your solution makes sense by making a rough estimate. For example, if you’re solving for a rate of change or area, estimate whether the answer is reasonable based on the context of the problem.
- Plug In Your Answer: If applicable, substitute your final solution back into the original equation or problem. If the solution satisfies the equation, you’ve likely done your work correctly. This is especially helpful for verifying solutions to equations or inequalities.
By using these verification techniques, you can confidently check your solutions and ensure the integrity of your work, which will help you avoid costly errors and boost your understanding of mathematical principles.
Reviewing Solutions to 2012 Questions
Reviewing solutions to past questions is an essential part of the learning process. It allows you to identify where you went wrong, reinforce concepts that were difficult, and build confidence in solving similar problems in the future. By carefully analyzing each solution, you gain a deeper understanding of the methods used and improve your problem-solving skills.
When reviewing solutions, consider the following steps to ensure a thorough and effective review:
- Understand the Approach: Look at how each solution is structured. Pay attention to the strategies and methods used to solve the problems. Understanding the underlying techniques will help you apply them to other questions in the future.
- Identify Mistakes: If you made an error, pinpoint exactly where you went wrong. Was it in the initial setup, a calculation mistake, or a misinterpretation of the problem? Recognizing the specific type of error helps you avoid repeating it.
- Compare with Alternative Solutions: Sometimes, there are multiple ways to solve a problem. Compare the solution you found with different methods or approaches. This can broaden your perspective and improve your flexibility when tackling similar questions.
- Check for Completeness: Make sure that each solution is fully explained and that no steps were skipped. A well-documented solution ensures that you understand not just the final result, but the reasoning behind each step.
- Seek Feedback: If possible, discuss your solutions with peers, teachers, or online communities. Getting different viewpoints can help clarify any misunderstandings and reinforce correct methods.
By carefully reviewing each solution, you can deepen your understanding, avoid repeating past mistakes, and become more adept at solving problems in future challenges.
Importance of Timing in the Exam
Time management is one of the most crucial skills to develop when preparing for a rigorous assessment. Properly allocating your time during the test ensures that you can answer all the questions without rushing, while still maintaining accuracy. Without effective timing, even the most prepared individuals may struggle to complete the test within the allotted period, leading to unnecessary stress and potentially missed opportunities to earn points.
Balancing Speed and Accuracy
In a high-pressure environment, it’s important to strike a balance between answering questions quickly and ensuring accuracy. Rushing through questions can result in careless errors, while spending too much time on a single problem can leave you with insufficient time for the rest of the test. Developing strategies to quickly assess the difficulty of each question will help you decide when to move on or devote extra time.
Effective Time Allocation Strategies
One way to manage your time is by setting benchmarks for each section of the test. Divide the total time into segments based on the number of questions and their complexity. For example, you might decide to spend a fixed amount of time on multiple-choice questions and a little more time on free-response sections. Regular practice under timed conditions is essential to refine your timing strategies and ensure that you can complete each section efficiently.
By mastering the art of time management, you can enhance your performance, reduce anxiety, and ensure that every part of the test receives the attention it deserves.
How to Interpret AP Exam Scoring
Understanding how scores are calculated and interpreted in a standardized assessment is key to evaluating your performance. Scoring systems are designed to measure both the accuracy of your responses and your overall proficiency in the subject. Each part of the test is weighted differently, and understanding these weights can help you interpret your score accurately and identify areas for improvement.
In many tests, the scoring system consists of raw scores, weighted scores, and overall scores, with each section contributing to the final result. The following table explains the general breakdown of how scores are typically interpreted:
| Section | Weight | Scoring Criteria |
|---|---|---|
| Multiple-Choice Section | 50% | Each correct answer contributes one point, and no points are subtracted for incorrect answers. |
| Free-Response Section | 50% | Points are awarded based on the completeness and correctness of your written solutions. Partial credit may be given. |
After scoring each section, the raw scores are converted into a composite score, which is then compared to a predetermined scale to assign a final score ranging from 1 to 5. A score of 5 indicates excellent performance, while a score of 1 generally suggests a need for improvement.
Knowing how the scoring system works allows you to better assess your strengths and weaknesses and plan your preparation strategy for future assessments.
AP Calculus AB Study Resources
Having access to the right study materials is essential for mastering complex mathematical concepts and performing well on standardized assessments. Effective resources provide structured guidance, practice problems, and explanations that help build both foundational knowledge and advanced skills. From textbooks and online tutorials to practice questions and interactive apps, a variety of tools can enhance your preparation.
Textbooks and Reference Guides
Textbooks remain one of the most reliable resources for studying mathematical concepts. They offer comprehensive explanations of topics, step-by-step examples, and practice exercises that reinforce key principles. Some recommended books include titles from renowned publishers like Kaplan and Princeton Review, which cover all the essential material and provide targeted practice for the subject matter.
Online Platforms and Tools
Online platforms such as Khan Academy and Coursera offer interactive lessons and videos that cater to different learning styles. These resources break down difficult topics into digestible segments, providing visual explanations and quizzes to test your knowledge. Additionally, apps like Wolfram Alpha can assist in solving complex equations and verifying solutions.
Incorporating a mix of these materials into your study plan will help ensure a thorough understanding of the subject and better equip you for any challenges that may arise during the assessment process.
Benefits of Practicing with Past Exams
Working through previous assessment papers offers a multitude of benefits for students preparing for rigorous tests. By engaging with questions from past years, learners can gain a deeper understanding of the material, improve their problem-solving skills, and become familiar with the format and timing of the actual test. This approach allows students to target areas of weakness while reinforcing their strengths, ultimately enhancing their readiness for the challenge ahead.
Improved Familiarity with Question Types
One of the most significant advantages of reviewing past papers is the opportunity to become familiar with the variety of questions that may appear in the assessment. By tackling a wide range of problems, students learn the patterns and themes commonly tested, which helps in developing strategies for answering similar questions. Repetition is key–the more often students practice with real test questions, the more confident and efficient they become in solving them under time pressure.
Enhanced Time Management Skills

Another key benefit of using previous papers for practice is the chance to develop time management skills. Students can simulate real test conditions by timing themselves during practice sessions. This experience teaches them how to allocate time effectively to each section and question. Practice under timed conditions is invaluable for building the stamina and mental focus needed to complete the entire assessment within the allocated time.
Incorporating past papers into your study routine provides not only an opportunity for targeted learning but also a boost in test-taking confidence, leading to better overall performance when the time comes.
What to Expect on the Exam Day

The day of the assessment is a crucial moment in your preparation journey. It’s important to approach it with confidence, knowing exactly what to expect and how to handle the various stages of the process. From arriving at the testing center to the final moments of completing your test, being prepared can help alleviate stress and ensure you perform at your best.
Before the Test
- Arrive Early: Ensure that you arrive with plenty of time to spare. This will give you the opportunity to settle in, find your seat, and mentally prepare for the challenge ahead.
- Bring Necessary Items: Double-check that you have all required materials, such as identification, pencils, erasers, and a calculator (if allowed). Having everything ready will save you from unnecessary stress.
- Stay Calm: Take deep breaths and focus on maintaining a positive attitude. Stress management is essential for performing well on the test.
During the Test
- Follow Instructions Carefully: Listen attentively to the proctor’s instructions. Make sure you understand the rules and guidelines before beginning.
- Time Management: Keep an eye on the clock and pace yourself. Allocate time for each section, ensuring that you don’t spend too long on any one question.
- Stay Focused: Maintain concentration throughout the test. If you find yourself stuck on a question, move on and come back to it later if time allows.
After the Test
- Stay Calm and Positive: Once the test is complete, take a moment to relax. The hard work is over, and you’ve done your best.
- Reflect: Think about your performance and what you’ve learned through the process. This can help guide your preparation for future challenges.
By being well-prepared and understanding the sequence of events on test day, you can approach the assessment with confidence, helping you to achieve the best possible result.