Understanding how to break down complex expressions into simpler components is an essential skill in mathematics. This process not only simplifies the calculations but also reveals the underlying structure of the problem. By learning to identify patterns and apply appropriate strategies, students can efficiently handle a wide range of mathematical challenges.
In this section, we will explore one of the most effective methods for addressing these types of problems. Through clear steps and well-organized approaches, you will learn how to approach problems systematically, ensuring accurate results every time. Whether you’re tackling basic forms or more intricate variations, this method will provide the tools needed to work through various scenarios with ease.
Mastering this approach requires a combination of understanding the principles and consistent application. Over time, as you continue to apply these techniques, your confidence and speed will increase, allowing you to handle even the most complex problems effortlessly.
Mastering Polynomial Solutions Through Simplification
Achieving proficiency in breaking down complex expressions is crucial for anyone looking to excel in mathematics. By learning how to simplify such forms, individuals can not only find solutions efficiently but also gain a deeper understanding of how various components interact. This approach allows for a structured and logical method to tackle seemingly difficult problems.
Understanding the Basic Steps
The first step in handling these challenges involves identifying the key parts of the expression. Once you recognize the terms and their relationships, you can apply specific techniques to rewrite the expression in a more manageable form. The main goal is to transform the original structure into a set of simpler components that can be easily solved.
Why This Approach Works
This method is based on the principle that expressions with similar structures can be rearranged into factors that make solving straightforward. By recognizing common patterns and applying consistent strategies, the process becomes more intuitive and less time-consuming. As a result, problems that initially seem daunting are simplified into smaller, more manageable steps.
| Step | Description |
|---|---|
| 1 | Identify the expression and its components |
| 2 | Look for common factors or patterns |
| 3 | Apply appropriate techniques to simplify |
| 4 | Rewrite the expression in factorized form |
| 5 | Find the solutions by setting each factor to zero |
Understanding the Basics of Factoring
Mastering the art of breaking down complex expressions into simpler components is a fundamental skill in mathematics. This approach helps transform a seemingly complicated problem into smaller, more manageable pieces. The key to success lies in recognizing patterns and applying the right methods to simplify the original structure.
At its core, the technique revolves around rewriting a given problem as a product of two or more terms. This allows for easier manipulation and solution finding. The process is similar to reversing the multiplication process, where you decompose a given expression into its simpler factors.
| Step | Description |
|---|---|
| 1 | Recognize the structure of the expression |
| 2 | Identify common factors or terms |
| 3 | Split the expression into simpler components |
| 4 | Apply reverse multiplication to isolate terms |
| 5 | Combine the factors to form the final solution |
Why Factoring Solves Polynomial Problems
Understanding why breaking down expressions into simpler components works is essential for mastering complex problems in algebra. The key idea behind this method is that when you rewrite a complicated expression as a product of simpler terms, it becomes easier to identify the solutions. By separating the factors, you can identify the specific values that satisfy the original structure.
The Role of Zero in the Process
The fundamental principle behind this method is the “zero product property.” This rule states that if the product of two terms equals zero, then at least one of those terms must also be zero. By applying this property to the factored form of an expression, you can quickly find the values that make the equation true. This transforms the problem into a simpler task of solving for individual variables.
Breaking Down the Problem Step-by-Step
When you apply this approach, you first break the expression into its components, identifying two or more factors. Afterward, you set each of these factors equal to zero and solve for the variable. This approach eliminates the need for complicated computations, making it a straightforward and effective method for finding solutions to these types of problems.
Key Methods for Factoring Polynomials
When working with complex expressions, it’s essential to apply the right techniques to break them down into simpler components. The goal is to identify patterns and utilize strategies that allow you to rewrite the original form in a way that’s easier to work with. Different methods can be used depending on the structure of the expression, each offering a unique approach to achieving the solution.
One of the most commonly used methods is grouping, which involves rearranging terms to identify common factors between pairs of terms. Another technique involves recognizing special patterns like perfect square trinomials, which can be quickly simplified. Both methods allow for efficient decomposition, making the problem more manageable.
Additionally, understanding how to handle expressions with multiple terms is crucial. By applying systematic approaches such as these, solving complex problems becomes a more straightforward task. As you become more familiar with these techniques, your ability to handle a wide range of problems will improve significantly.
How to Factor Perfect Square Trinomials
Recognizing and simplifying certain types of expressions can make solving problems much faster. A perfect square trinomial is one of these special forms that can be easily broken down into the product of two identical binomials. Identifying this structure is key to simplifying and solving the problem with minimal effort.
To factor a perfect square trinomial, start by recognizing the pattern. The first and last terms must be perfect squares, and the middle term must be twice the product of the square roots of the first and last terms. Once this pattern is identified, the trinomial can be rewritten as the square of a binomial, making the entire process much easier to manage.
For example, an expression like x² + 6x + 9 is a perfect square trinomial. The first term, x², is the square of x, the last term, 9, is the square of 3, and the middle term, 6x, is twice the product of x and 3. Therefore, it can be factored as (x + 3)².
Factoring by Grouping Explained Simply
One of the most effective ways to simplify expressions with four terms is by grouping. This method involves reorganizing the terms into pairs and factoring each pair separately. Once each pair is simplified, common factors can be identified, leading to a much more manageable expression. The key to success with this approach is recognizing how the terms interact with each other.
Start by splitting the original expression into two groups that each have common factors. After factoring the terms in each group, you’ll often find that both groups share a common binomial factor. Once this shared factor is identified, you can then factor it out, resulting in a simplified expression.
For example, consider the expression ax + ay + bx + by. First, group the terms as (ax + ay) and (bx + by). Factor out the common factors from each group: a(x + y) and b(x + y). Now, you can factor out the common binomial (x + y), giving you (x + y)(a + b).
Common Mistakes When Factoring Equations
While simplifying complex expressions, it’s easy to overlook certain details, leading to mistakes that can throw off your entire solution. Many errors stem from misidentifying patterns or failing to factor completely. Understanding the common pitfalls can help you avoid these issues and improve your accuracy when working through these problems.
Forgetting to Factor Completely
One frequent mistake is stopping the process too early. Sometimes, after factoring out the greatest common factor (GCF) or simplifying the terms, the expression may seem simplified enough, but it still contains factors that need to be broken down further. Always double-check that you’ve fully simplified the terms and completed the factorization.
Misapplying the Zero Product Property
Another common error is incorrectly applying the zero product property. This rule states that if two factors multiply to zero, one or both of the factors must be zero. Sometimes, people forget to set each factor equal to zero or mistakenly leave out one of the factors, which results in incomplete solutions.
To avoid these mistakes: Always ensure that you have fully simplified the expression before proceeding and remember to check each factor carefully. Double-check your work to catch any steps you may have missed.
Step-by-Step Guide to Solving Equations
Breaking down complex problems into manageable steps is key to finding the correct solution. By following a systematic approach, you can simplify even the most difficult expressions. This guide outlines the essential steps for approaching these problems, ensuring that you understand the process from start to finish.
Start by rearranging the terms to create a clear structure. Identify any common factors and simplify the expression as much as possible. Once this is done, you can proceed to the next step, where you focus on finding the values that satisfy the simplified form.
After simplifying, apply relevant rules or methods to isolate the variable. This may involve rewriting terms or breaking the expression into smaller components. Once all the terms are isolated, you can solve for the variable, ensuring that each step is verified and that no detail is overlooked.
Real-Life Applications of Factoring
Understanding how to break down complex expressions is not only useful in mathematics but also in various real-world situations. Many fields, such as engineering, physics, economics, and computer science, rely on the ability to simplify and solve problems that involve complex relationships between variables. By mastering the techniques of simplification, you can approach practical challenges with greater efficiency and precision.
For instance, in engineering, simplifying formulas is often necessary to model physical systems. Whether it’s calculating the dimensions of a structure or determining the forces acting on an object, the ability to break down complicated relationships into simpler components makes solving these problems more feasible. Similarly, in economics, simplifying equations helps in understanding market trends, optimizing resource allocation, and making cost-effective decisions.
Even in computer science, algorithms often use simplified mathematical models to process data or predict outcomes. By mastering these methods, professionals can create more efficient programs and systems. In everyday life, factoring helps in budgeting, planning, and other decision-making tasks by allowing people to break down problems and analyze individual components.
Checking Solutions After Factoring
After simplifying a problem and identifying potential solutions, it’s important to verify that these solutions are correct. This process ensures that no errors were made during the simplification and that the identified values truly satisfy the original problem. Without this step, it’s possible to overlook mistakes or find inaccurate results.
Substituting Values Back into the Original Expression
The most straightforward way to verify your solutions is to substitute them back into the original form. By doing so, you can check if both sides of the expression balance correctly. If the substituted values satisfy the equation, then the solutions are correct; otherwise, you may need to recheck the factorization or steps taken.
Using a Different Approach for Cross-Verification
Another method to confirm the accuracy of the solutions is by using an alternative technique. If one method of simplification was used, try a different approach to see if it yields the same results. This cross-verification helps ensure consistency and provides greater confidence in the solutions you’ve found.
Remember: Always double-check your work and verify that the solutions meet the conditions of the problem. This extra step can help prevent small mistakes that could lead to incorrect results.
How to Factor Quadratics with Leading Coefficients
When dealing with expressions where the first term is not just a simple variable squared, factoring requires a bit more effort and strategy. These cases typically involve an additional constant that affects the overall simplification process. To handle such problems, you need to carefully break down the expression in a way that allows for the correct identification of factors.
One of the most effective methods for these types of problems is the “splitting the middle term” technique. This process involves finding two numbers that multiply to the product of the first and last terms, while also adding up to the middle term. Here’s how you can approach it:
- Step 1: Identify the leading coefficient (the number multiplying the first term) and the constant term.
- Step 2: Multiply the leading coefficient by the constant term.
- Step 3: Find two numbers that multiply to the result from Step 2 and add to the middle term.
- Step 4: Rewrite the middle term using these two numbers.
- Step 5: Group the terms and factor each group separately.
- Step 6: Factor out the common binomial factor from both groups.
For example, consider the expression 6x² + 5x – 6. The first step is to multiply 6 (the leading coefficient) by -6 (the constant term), which gives -36. Next, find two numbers that multiply to -36 and add up to 5. These numbers are 9 and -4. Rewrite the middle term as 6x² + 9x – 4x – 6. Now, group the terms: (6x² + 9x) – (4x + 6). Factor each group: 3x(2x + 3) – 2(2x + 3). Finally, factor out the common binomial: (2x + 3)(3x – 2).
This method works by transforming the original problem into something more manageable, allowing you to identify the factors correctly and simplify the expression efficiently.
Handling Negative Numbers in Factoring
When working with expressions that involve negative values, it’s important to approach the process with care. Negative numbers can sometimes complicate the task of simplifying and identifying factors, but understanding how to manage them can make the entire process smoother. The key lies in recognizing how negative signs affect the multiplication and addition of terms.
One common challenge is dealing with a negative constant or coefficient, especially when looking for two numbers that both multiply and add to specific values. Here’s how you can handle such situations:
- Identifying Product and Sum: First, look for two numbers that multiply to give the product of the leading coefficient and the constant term. If either of these numbers is negative, you will need to account for it in the next step.
- Dealing with Signs: When one or both numbers are negative, pay close attention to how the signs will affect the sum. For instance, if the product is negative, one of the factors must be negative, and the other must be positive.
- Splitting the Middle Term: When dealing with negative numbers, be sure to rewrite the middle term carefully. For example, in a case where the two numbers multiply to a negative value and sum to the middle term, adjust the signs so that the correct pair is used to rewrite the expression.
For example, consider the expression x² – 5x – 6. To factor it, you need two numbers that multiply to -6 (the constant) and add to -5 (the middle term). The numbers -6 and 1 work because -6 × 1 = -6, and -6 + 1 = -5. After rewriting the expression as x² – 6x + x – 6, group the terms: (x² – 6x) + (x – 6). Then factor out the common terms from each group: x(x – 6) + 1(x – 6). Finally, factor out the common binomial: (x + 1)(x – 6).
By carefully handling negative numbers, you can successfully factor expressions that initially seem more challenging. Understanding how to manipulate the signs and apply them correctly is an essential skill in simplifying mathematical problems.
Using the Zero Product Property Effectively
The Zero Product Property is a powerful tool that allows you to find solutions to problems involving products of terms. When the product of two or more factors equals zero, at least one of the factors must be zero. This principle can simplify many algebraic challenges by providing a straightforward way to determine the values that make an expression true.
To use this property effectively, it is essential to first rewrite the expression in a form where it is set equal to zero. Once this is done, you can then split the expression into its individual factors and set each factor equal to zero.
Steps for Applying the Zero Product Property
- Rearrange the Expression: Begin by ensuring that the expression is set equal to zero. If necessary, move terms around to achieve this.
- Factor the Expression: Once you have a zero on one side, factor the remaining terms as much as possible.
- Set Each Factor Equal to Zero: After factoring, break the expression into separate equations. Set each factor equal to zero and solve for the variable.
- Find All Solutions: Solve each individual equation to find the possible values for the variable.
For example, consider the equation x² – 5x + 6 = 0. First, factor it as (x – 2)(x – 3) = 0. Next, set each factor equal to zero: x – 2 = 0 and x – 3 = 0. Solving these gives the solutions x = 2 and x = 3.
Why It Works
The Zero Product Property works because if the product of multiple factors equals zero, at least one of the factors must be zero. This helps narrow down the possible values for the variable, making the problem much easier to solve. It is especially useful when dealing with factored expressions, as it allows you to break the problem down into simpler parts.
By mastering the use of the Zero Product Property, you can efficiently solve many types of algebraic problems and quickly find the values that satisfy an equation.
Advanced Factoring Techniques for Quadratics

When dealing with more complex problems, it’s important to move beyond basic methods and explore advanced techniques for breaking down expressions. These strategies involve recognizing patterns and using specific formulas that can simplify the process, helping to find solutions quickly and accurately. Mastering these methods is key to tackling harder problems with confidence.
One such advanced technique is the use of splitting the middle term, which requires breaking down the linear term into two parts that make the expression easier to handle. Another powerful approach involves using the method of completing the square, which transforms the expression into a perfect square trinomial.
Techniques for Advanced Factorization
- Splitting the Middle Term: This technique involves identifying two numbers that multiply to give the product of the leading coefficient and the constant term, while adding up to the middle term. This allows you to rewrite the expression in a more easily factorable form.
- Completing the Square: By adding a specific value to both sides of the expression, this method creates a perfect square trinomial that can be factored as a binomial squared.
- Using the Difference of Squares: If the expression contains terms that are perfect squares, you can apply this formula: a² – b² = (a + b)(a – b). This helps break down complex expressions efficiently.
- Factoring by Grouping: When the expression contains four terms, grouping them into pairs that share common factors can simplify the process. This method is especially useful for expressions with multiple variables.
Example of Advanced Techniques
Consider the expression 6x² + 11x – 35. To factor this using the splitting the middle term technique, we look for two numbers that multiply to 6 * -35 = -210 and add up to 11. These numbers are 21 and -10. Rewrite the middle term as 21x – 10x, and then factor by grouping:
- Group: (6x² + 21x) – (10x – 35)
- Factor each group: 3x(2x + 7) – 5(2x + 7)
- Factor out the common binomial: (3x – 5)(2x + 7)
By applying advanced techniques like these, you can factor more complicated expressions that are otherwise difficult to manage with basic methods.
How Factoring Connects to Other Math Topics
Breaking down complex expressions into simpler components is an essential skill in mathematics that connects to a wide range of other topics. Whether it’s simplifying problems in algebra, finding solutions in geometry, or handling advanced concepts in calculus, the ability to manipulate and transform expressions is fundamental. This technique serves as a bridge that ties together different areas of math, helping you approach new challenges with confidence and ease.
By mastering the art of breaking down polynomials and expressions, you unlock the ability to simplify a wide variety of problems. This skill plays a crucial role in understanding functions, working with systems of equations, and even solving problems in geometry and calculus. The connections between these topics show how a single approach can be applied across different mathematical fields to solve a diverse range of problems.
Applications Across Mathematical Disciplines
- Algebra: Simplifying terms and recognizing common factors are core aspects of algebra, helping to solve for unknown values and manipulate equations efficiently.
- Geometry: When working with areas and volumes, simplifying algebraic expressions is key, especially when calculating the dimensions of geometric shapes or working with spatial properties.
- Calculus: In calculus, understanding how to break down complex functions into simpler forms is essential for finding derivatives and limits, which are foundational to the subject.
- Systems of Equations: Simplifying expressions is particularly helpful when working with multiple equations, where finding common factors can lead to easier solutions.
Real-World Examples in Other Math Fields
In geometry, for instance, when calculating areas, simplifying the expressions for rectangles, circles, or triangles can involve breaking them down into smaller parts. Similarly, in calculus, simplifying a function by identifying its components makes it easier to calculate derivatives and integrals. This approach is used not only to simplify the problem but to identify patterns that lead to faster solutions.
| Mathematical Field | Application of Expression Simplification |
|---|---|
| Algebra | Solving for unknowns and simplifying terms |
| Geometry | Finding areas and volumes, working with spatial properties |
| Calculus | Breaking down complex functions for easier derivative and limit calculations |
| Systems of Equations | Simplifying and solving multiple equations |
The connections between this technique and other areas of mathematics underscore its importance in both foundational and advanced mathematical learning. Whether you’re solving simple problems or dealing with complex concepts, this skill remains indispensable.
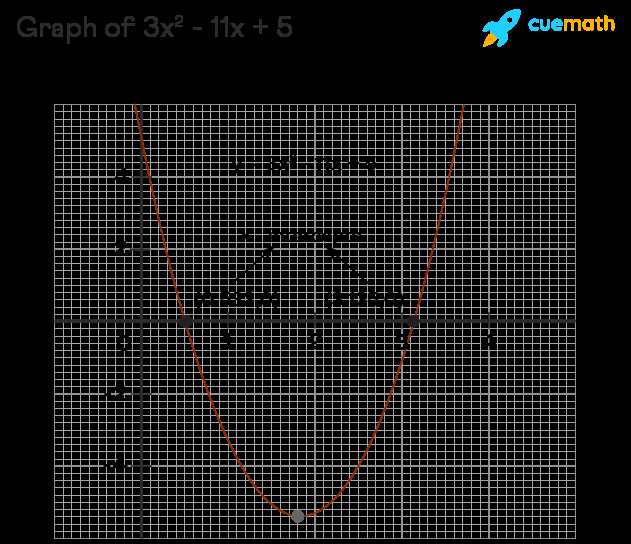
Visualizing Factoring on Graphs
Understanding how mathematical expressions can be represented visually provides deeper insights into their structure and behavior. By translating algebraic relationships into graphical form, we can see how changes in variables influence the overall outcome. This connection allows for a more intuitive grasp of the underlying principles, particularly when dealing with expressions that have multiple terms. Graphs offer a powerful tool for visualizing how a given expression behaves and how it can be simplified or manipulated.
When we graph certain functions, the x-intercepts often reveal key insights into the values that satisfy the expression. These intercepts, where the graph crosses the x-axis, are directly related to the roots or solutions of the expression. Visualizing these intersections allows us to identify patterns and relationships that are not immediately apparent from the algebraic form alone.
Understanding the Connection Between Roots and Graphs
The roots or solutions of an expression correspond to the points where the graph intersects the x-axis. These intersections are important because they tell us the values that make the expression equal to zero. The process of simplifying or breaking down an expression often involves finding these points of intersection, which can be easily seen on a graph. This provides a clear visual representation of the relationships between variables.
How to Interpret Graphical Representations
- Roots: The x-intercepts of a graph indicate where the expression evaluates to zero. These are the values that satisfy the expression.
- Symmetry: Many expressions exhibit symmetrical properties, which can be seen in the shape of the graph. Recognizing this symmetry helps identify important features such as the vertex or the axis of symmetry.
- Behavior of the Graph: The shape and direction of the graph reveal important details about the nature of the expression. For example, a parabola may open upwards or downwards depending on the coefficients of the terms.
By analyzing the graph of an expression, we can gain a deeper understanding of its structure and the values that satisfy it. This visual approach not only simplifies the process of working with expressions but also enhances problem-solving skills by providing a clear, tangible representation of the mathematical concepts at hand.
Why Practice is Crucial for Mastery
Mastering any skill, particularly in mathematics, requires more than just theoretical understanding. It involves consistent effort and repeated application of the concepts to build confidence and fluency. Just like learning a musical instrument or playing a sport, refining one’s abilities in math is achieved by regularly working through problems and encountering different variations of the same concepts. This active engagement allows individuals to internalize techniques and better recognize patterns that may not be obvious at first glance.
Building Confidence Through Repetition
Repetition allows learners to become more comfortable with the material, reducing anxiety and increasing the ability to quickly recall methods and apply them effectively. When students repeatedly engage with problems, they begin to recognize common features and strategies, which leads to faster, more accurate results. This confidence is crucial for tackling more complex problems that require advanced thinking and problem-solving skills.
Developing Problem-Solving Skills
Engaging with a variety of problems helps develop critical thinking and problem-solving skills. The more one works with different types of challenges, the better equipped they become to approach unfamiliar problems with a clear strategy. This adaptability is a key component of mastering mathematical concepts and ensuring long-term success.
In conclusion, achieving mastery in any subject is not a matter of memorizing formulas or procedures but rather honing the ability to apply these techniques with ease and accuracy. Regularly working through problems helps solidify knowledge and fosters the development of both confidence and critical thinking abilities.
Tips for Speed and Accuracy in Factoring
Achieving both speed and accuracy in mathematical procedures requires a balance of understanding, familiarity, and focus. By developing certain habits and strategies, individuals can approach problems more efficiently without sacrificing precision. Whether you’re working through basic or more complex tasks, there are effective methods to improve both your speed and the correctness of your solutions.
Understanding Patterns and Techniques
One of the key factors in improving efficiency is recognizing recurring patterns and applying the right technique to each type of problem. For example, familiarizing yourself with standard forms and their corresponding approaches can drastically reduce the time spent figuring out the method for each challenge.
- Know common forms: Understand common types of problems and their solutions, such as special products (e.g., difference of squares, perfect squares).
- Use shortcuts: When applicable, use shortcuts or special rules that apply to certain types of problems (like factoring by grouping).
- Work backward: If you’re stuck, try reversing the process to check your steps or to identify patterns that may simplify the work.
Practice Mental Calculations
Being able to perform calculations mentally can significantly speed up the process. This is particularly useful when dealing with smaller numbers or simpler problems where extensive writing or use of a calculator isn’t necessary. Strengthening your ability to perform quick calculations will help you reduce errors and save time.
- Break down numbers: Instead of multiplying large numbers all at once, break them down into smaller, manageable parts to handle mentally.
- Use estimation: Estimate answers where possible to quickly determine if you’re on the right track, especially when working with coefficients or constants.
- Memorize key formulas: Remember essential formulas and relationships so you don’t waste time looking them up during the process.
By regularly practicing these techniques and honing your skills, you can boost both your speed and accuracy, making even the most complex problems easier to handle efficiently.