
Preparing for a key math exam can be overwhelming, especially when trying to ensure you’ve covered every important concept. To succeed, it’s essential to revisit core ideas and refine problem-solving strategies. This section provides a detailed guide for tackling the final evaluations that test your understanding and application of mathematical skills.
Understanding the material and practicing regularly are crucial steps toward mastery. While reviewing questions, it’s important to focus not just on solutions but also on the reasoning behind each step. By addressing common challenges and identifying areas of improvement, you can build the confidence needed to excel when the real assessment comes.
In the following sections, you’ll find clear explanations and strategies for handling various mathematical problems, allowing you to focus on the methods that bring the best results. Emphasizing logical steps and effective techniques will give you the tools to approach any question with ease.
Algebra 1 Test Answer Breakdown

Understanding the reasoning behind each solution is crucial for mastering mathematical evaluations. It’s not enough to simply arrive at the correct result; it’s important to break down the steps and understand why they lead to that conclusion. This approach will help you tackle similar problems with greater confidence and precision.
Step-by-Step Explanation
When reviewing a question, the first step is to identify the key concepts involved. Whether it’s solving an equation, graphing a function, or simplifying an expression, recognizing the core technique needed will guide your approach. Once you’ve identified the method, carefully follow each operation and be mindful of any rules that apply. For instance, if you’re solving for an unknown, make sure every step adheres to the rules of equality or inverse operations.
Common Pitfalls to Avoid
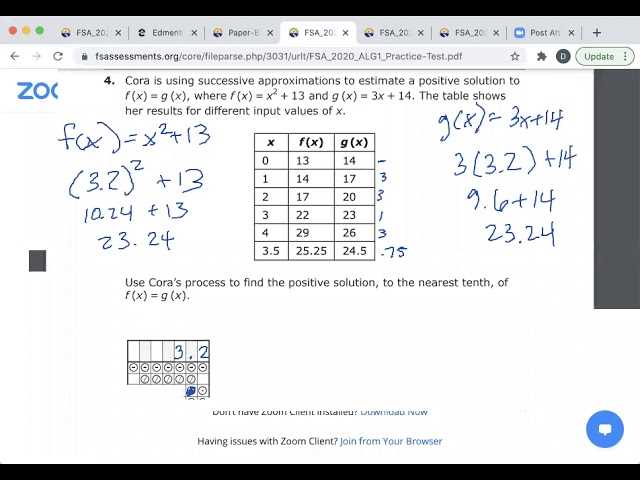
As you analyze each solution, it’s important to be aware of common mistakes that can easily occur during calculations. For example, sign errors, misinterpreting an equation’s structure, or forgetting to apply a property correctly can all lead to incorrect results. Taking extra time to check your work after each step is an excellent way to ensure accuracy and avoid these frequent errors.
Mastering Key Algebra 1 Concepts
To succeed in mathematical assessments, it’s essential to understand and master the core principles that form the foundation of the subject. These fundamental concepts are the building blocks that enable you to solve problems efficiently and accurately. By focusing on these key ideas, you can improve both your problem-solving skills and your overall performance.
Below is a table outlining some of the most critical concepts you should focus on. These areas are commonly tested and understanding them deeply will significantly boost your ability to handle a variety of questions:
| Concept | Description |
|---|---|
| Equations | The process of finding the value of variables that satisfy a given mathematical statement. |
| Functions | Relations that assign exactly one output for each input, often expressed in equation form. |
| Inequalities | Expressions that compare values using signs such as greater than, less than, or equal to. |
| Exponents | The operation of raising numbers to a certain power, which simplifies multiplication and division. |
| Factoring | Breaking down expressions into products of simpler terms to simplify equations or expressions. |
Focusing on these areas will enhance your ability to approach a wide range of problems with confidence and clarity. Mastery of these fundamental topics will also make more advanced concepts easier to understand as you progress in your studies.
Common Mistakes to Avoid on Tests
During an important assessment, it’s easy to make small errors that can affect your performance. These mistakes often arise from rushing through questions or misinterpreting instructions. By being aware of the most common pitfalls, you can take steps to avoid them and improve your accuracy under pressure.
Skipping Crucial Steps
One of the most frequent mistakes is skipping essential steps in the problem-solving process. It’s tempting to try and solve an equation quickly, but skipping intermediate steps can lead to errors that compound as the problem progresses. Always take the time to work through each stage methodically, even if you feel confident about the answer.
Misinterpreting Symbols and Notations
Another common issue is misunderstanding symbols and notations used in mathematical expressions. For instance, mistaking a negative sign for subtraction or confusing the order of operations can lead to incorrect results. Pay careful attention to each symbol, especially in complex problems where small errors can have a significant impact on the outcome.
Effective Study Tips for Algebra 1
To truly excel in mathematical evaluations, a well-structured study routine is essential. Rather than simply reviewing content, effective preparation involves focusing on understanding the core principles, practicing regularly, and refining problem-solving techniques. Below are several proven strategies to help you study efficiently and retain the material:
- Break Down Complex Problems: Start by dividing complicated problems into smaller, manageable parts. This approach makes it easier to understand each step and avoid errors.
- Use Practice Questions: Consistent practice is crucial. Work through a variety of questions to strengthen your skills and get comfortable with different problem types.
- Study in Short Sessions: Instead of cramming for hours, break your study time into focused intervals. Short, frequent sessions are more effective than long, drawn-out ones.
- Review Mistakes: After practicing, go over any mistakes you made. Understanding why something went wrong is key to improving your skills.
- Use Visual Aids: Diagrams, charts, and other visual tools can help you grasp abstract concepts and improve retention.
These methods will help you approach your studies in a more organized and effective manner, leading to better understanding and improved performance during evaluations. Consistency, patience, and strategic practice are key to mastering the material and achieving success.
Understanding Practice Test Solutions
To fully grasp mathematical concepts, it’s crucial to understand not only the correct results but also the steps that lead to those results. Reviewing solutions thoroughly helps to identify where mistakes may have occurred and reinforces the methods used to solve each problem. By carefully analyzing each solution, you can improve your problem-solving approach and gain deeper insight into the material.
- Break Down Each Step: Don’t just focus on the final answer; go through each step of the solution to understand how it was reached. Pay attention to the operations, rules, and properties applied at each stage.
- Identify Key Concepts: Every problem is built around certain principles. Recognizing these concepts as you review solutions helps reinforce your understanding and application of them in future problems.
- Compare Different Approaches: If a solution involves multiple methods, compare them to see how different techniques can lead to the same result. This will expand your problem-solving toolkit.
- Learn from Mistakes: When reviewing solutions, pay particular attention to any errors you may have made. Understanding why a mistake occurred will help you avoid similar issues in the future.
- Practice Regularly: Consistent review and solving similar problems will help cement your understanding of the methods used in the solutions.
By taking the time to thoroughly examine each solution, you can improve both your understanding and your ability to apply mathematical methods effectively. Mastery comes not just from getting the right answer, but from knowing why and how that answer was achieved.
How to Use Test Answers Wisely
Simply knowing the correct results to problems is not enough to improve your skills. The key to mastering mathematical concepts lies in understanding the process behind each solution. By reviewing and reflecting on the solutions, you can better grasp the strategies used and apply them to future problems. Using the provided solutions wisely allows you to enhance your approach and avoid repeating mistakes.
Here’s a guide on how to make the most of the solutions you’ve reviewed:
| Strategy | Purpose |
|---|---|
| Analyze Each Step | Focus on the methods and operations used, and understand why they were applied at each stage. |
| Identify Mistakes | Look for any errors in your own process and learn from them to avoid repeating them in the future. |
| Compare Approaches | Compare the solution to your own approach to see if there’s a more efficient or accurate method. |
| Reapply Methods | Use the steps and strategies from the solution to solve similar problems, reinforcing your understanding. |
| Focus on Concepts | Ensure that you fully understand the underlying concepts, rather than just memorizing steps. |
By applying these strategies, you can transform simple solutions into valuable learning experiences that will help you strengthen your skills and perform better in future evaluations.
Step-by-Step Answer Explanations
Breaking down each solution into clear, manageable steps is crucial for understanding the reasoning behind the final result. Rather than simply focusing on the end result, it is essential to follow through with each stage of the process. This method allows you to understand the logic, avoid mistakes, and build the skills necessary to solve similar problems in the future.
The following steps illustrate how to approach a typical problem and understand the process behind the solution:
- Identify the Given Information: Start by recognizing all the details provided in the problem. This includes constants, variables, and any additional conditions that affect the equation.
- Choose the Right Method: Based on the problem type, select the appropriate strategy to solve it–whether it’s isolating a variable, simplifying an expression, or applying a specific property.
- Perform Operations: Carefully execute the necessary mathematical operations, such as addition, subtraction, multiplication, or division. Be meticulous in applying each operation correctly.
- Simplify the Expression: After performing the operations, simplify the result if possible. This might involve factoring, combining like terms, or reducing fractions.
- Double-Check the Solution: Before finalizing your answer, review each step to ensure there are no calculation mistakes. If possible, substitute the solution back into the original problem to verify its correctness.
By following this step-by-step approach, you’ll develop a deeper understanding of the processes involved in solving problems. Each step builds upon the last, and with practice, you’ll gain the confidence and skill needed to handle even more complex problems with ease.
Essential Algebra 1 Topics to Review

To perform well in any mathematical evaluation, it’s important to master a variety of fundamental concepts. A strong grasp of the core topics will help you solve problems more efficiently and with greater confidence. Reviewing these key areas will not only prepare you for assessments but will also solidify your overall understanding of mathematical principles.
Key Areas to Focus On

- Linear Equations: Understanding how to solve equations with one variable, including techniques like isolating the variable and applying inverse operations.
- Exponents and Powers: Familiarize yourself with the rules of exponents, including multiplication, division, and raising powers to powers.
- Factoring: Review how to factor quadratic expressions and solve for variables in factored forms.
- Functions and Graphing: Learn how to interpret and graph functions, as well as understanding domain and range.
- Systems of Equations: Study methods for solving systems, including substitution, elimination, and graphical approaches.
- Inequalities: Focus on solving and graphing inequalities, and understanding how to work with compound inequalities.
Techniques to Strengthen Understanding

- Practice Word Problems: Translate real-world scenarios into mathematical equations to apply concepts in context.
- Use Visual Aids: Graphing and drawing diagrams can help visualize relationships and better understand abstract concepts.
- Review Past Mistakes: Reflect on errors made in previous exercises and identify patterns or concepts that need more attention.
By revisiting these essential topics, you’ll build a strong foundation that will make more complex concepts easier to understand and help you approach future problems with greater efficiency and accuracy.
Preparing for the Algebra 1 Final
As you approach the final evaluation in mathematics, preparation becomes key to achieving success. The final exam typically covers a wide range of topics, and having a structured approach to studying will help you tackle each section with confidence. Whether you’re reviewing specific problem types or brushing up on core concepts, strategic preparation will make all the difference.
Start by identifying the key topics you’ve learned throughout the course. Create a study plan that covers these areas and allocate time to each one based on your strengths and weaknesses. It’s also important to practice with different problem sets to familiarize yourself with various question formats and challenge yourself with problems that may appear in the evaluation.
Don’t forget to make use of available resources, such as review sheets, sample problems, and past assessments. Studying actively, rather than passively reviewing notes, will help reinforce your understanding and improve recall during the exam. Lastly, ensure you’re getting enough rest and managing stress, as a clear mind will help you perform at your best when it’s time to take the test.
Strategies for Time Management During Tests

Effective time management is a crucial skill when approaching any type of evaluation. With a limited amount of time to complete a series of problems, it’s important to prioritize tasks, allocate time wisely, and stay focused throughout the process. By using proven strategies, you can ensure that you make the most of the time available and avoid rushing through problems.
Start by quickly scanning the entire set of questions before diving into the first one. This gives you an overview of the content and helps you identify the sections that you are most confident in. Begin with the questions that you find easiest, as this will help you build momentum and ensure that you get those points first.
Next, set time limits for each section or group of problems. For example, if you have an hour for the exam and there are 60 questions, aim to spend no more than a minute on each one. Keep an eye on the clock, but avoid checking it too often, as this can cause unnecessary stress.
If you come across a particularly challenging question, don’t get stuck on it for too long. Mark it and move on, returning to it after you have completed the other questions. This prevents you from losing valuable time on a single problem and helps maintain your overall pace.
Lastly, always leave a few minutes at the end to review your work. This allows you to catch any mistakes and ensures that you haven’t overlooked any questions. Practicing these strategies regularly will improve your efficiency and help you manage your time effectively during any assessment.
Building Confidence for Algebra 1 Exams
Confidence plays a key role in your ability to perform well during any evaluation. When you feel assured in your knowledge and problem-solving abilities, you approach each question with a calm and focused mindset. Developing this confidence takes time and practice, but with the right approach, you can build it effectively before your assessment.
Key Strategies for Boosting Confidence
- Consistent Practice: The more you practice, the more familiar you become with different problem types and solutions. This repetition builds confidence in your skills.
- Break Down Complex Problems: When faced with a difficult problem, break it down into smaller, more manageable parts. This method reduces anxiety and allows you to focus on one step at a time.
- Use Positive Reinforcement: Celebrate small wins. Completing practice problems successfully boosts your morale and reinforces your abilities.
- Review Mistakes: Instead of getting discouraged by errors, review them to understand where things went wrong. This turns mistakes into valuable learning experiences.
Building a Supportive Environment
- Study Groups: Working with peers can help reinforce learning. Explaining concepts to others strengthens your own understanding and offers new perspectives.
- Ask for Help: Don’t hesitate to ask teachers or tutors for clarification on challenging topics. Understanding a difficult concept fully can significantly boost your confidence.
- Visual Aids: Diagrams, charts, and visual representations of problems can simplify complex ideas and make you feel more confident in your ability to solve them.
By consistently practicing, breaking down challenges, and seeking support when needed, you will gradually build the confidence necessary to approach any assessment with assurance and clarity.
How Practice Tests Improve Performance
Simulated evaluations are an invaluable tool for improving overall performance in any academic subject. By engaging with these mock assessments, students can familiarize themselves with the format and structure of real evaluations, while also identifying areas that need further attention. Repeated exposure to similar questions enhances problem-solving speed and accuracy, ultimately boosting confidence and efficiency.
Enhanced Familiarity with Question Types
Working through simulated problems allows you to become familiar with various question formats and their respective challenges. The more you interact with these types of problems, the more adept you become at recognizing patterns and applying appropriate strategies for solving them. This familiarity reduces anxiety on the actual assessment and helps you approach each problem with a clear, methodical mindset.
Identifying and Addressing Weak Areas

One of the most valuable benefits of engaging in simulated evaluations is the ability to pinpoint specific areas of weakness. As you work through the questions, you’ll notice patterns in the mistakes you make, which can highlight gaps in your understanding. By reviewing these errors, you can target specific concepts or skills that need further practice, ensuring that you approach the actual assessment fully prepared.
In addition to improving content knowledge, mock assessments help you develop critical test-taking skills, such as time management and stress reduction, which are key to excelling under pressure.
Solving Word Problems in Algebra 1
Word problems can often feel challenging due to the need to translate real-world scenarios into mathematical expressions. However, by breaking down the problem step by step, you can make the process more manageable. The key lies in understanding what the problem is asking and identifying the important information that needs to be used in calculations. With practice, these problems become easier to solve, and you can apply systematic methods to arrive at the correct solutions.
Steps for Tackling Word Problems:
- Read Carefully: Begin by reading the problem carefully and identifying the key pieces of information. Highlight or underline important values and relationships.
- Define Variables: Decide what the unknowns are and assign variables to represent them. This will help you organize your thoughts and form equations.
- Translate Words into Equations: Convert the written information into a mathematical form. Use the relationships between the variables and constants to set up an equation.
- Solve the Equation: Once the equation is set up, solve for the unknowns using appropriate methods such as substitution or elimination.
- Check the Solution: After solving, plug the values back into the original problem to ensure they make sense in the given context.
For example, consider a problem that involves a person purchasing several items. First, identify the cost of each item, then set up an equation based on the total cost. Solving this equation will give you the number of items purchased or the cost of each item, depending on the unknown.
By following these steps, you can effectively solve word problems and build the confidence needed to approach them with ease. Practice is essential, as the more problems you solve, the more adept you will become at recognizing patterns and applying the correct strategies.
Interpreting Graphs and Equations Correctly
Understanding how to read and interpret graphs and mathematical expressions is essential for solving problems accurately. Graphs provide a visual representation of relationships between variables, while equations offer a concise way to express these relationships algebraically. Being able to interpret both correctly allows you to gain insights into trends, patterns, and solutions that are not immediately obvious from the numbers alone.
When working with graphs, focus on key elements such as the axes, scale, and points plotted. Each point on the graph represents a specific relationship between the variables. Understanding the slope, intercepts, and the overall shape of the graph can help you deduce important information about the problem, such as rates of change or the values at specific points.
Equations, on the other hand, provide a direct way to relate variables. It is crucial to recognize the structure of the equation–whether it’s linear, quadratic, or another form–as this will guide you in solving for unknown values. Be mindful of operations such as addition, subtraction, multiplication, and division, and how they influence the relationship between the variables.
By practicing the interpretation of both graphs and equations, you develop a deeper understanding of how mathematical concepts work together. This skill helps you not only in exams but also in applying mathematical thinking to real-life situations, where interpreting data and relationships is key.
Resources to Enhance Your Algebra Skills
Improving your skills in solving mathematical problems requires access to the right resources that can provide support, practice, and detailed explanations. Whether you’re looking for interactive platforms, textbooks, or video tutorials, there are a variety of tools available to help you master concepts and perform well in assessments.
Using educational websites, mobile apps, and online forums is a great way to reinforce what you’ve learned and address areas where you may need more practice. These resources often offer step-by-step guides, problem sets, and solutions that can be customized to your learning level.
Additionally, textbooks and workbooks designed for learners at different levels can provide a structured way to progress. Many of these texts come with solutions and explanations that can help you better understand how to approach and solve complex problems.
| Resource Type | Description | Example Resources |
|---|---|---|
| Online Platforms | Interactive lessons and problem-solving tools | Khan Academy, IXL, Mathway |
| Video Tutorials | Step-by-step instructions for complex topics | YouTube channels, Coursera, edX |
| Textbooks & Workbooks | In-depth coverage with exercises and solutions | Pre-Algebra Workbooks, College Algebra Textbooks |
| Mobile Apps | On-the-go learning with practice problems and quizzes | Photomath, Wolfram Alpha |
Incorporating a variety of these resources into your study routine will help solidify your understanding, making it easier to apply mathematical concepts in different contexts. Whether you prefer self-paced learning or need direct assistance, there’s a wide range of tools to suit your needs.
How to Identify Your Weak Areas
Understanding where you struggle the most is a key part of improving your skills. Identifying weak areas allows you to focus your efforts on specific concepts that need attention, rather than wasting time on areas you already understand. This targeted approach ensures a more efficient and effective learning process.
To find these challenging areas, start by reviewing past work. Look for patterns in mistakes, whether they occur in particular types of problems or topics. Take note of any concepts that consistently cause difficulty, and make those a priority in your study sessions.
Utilize Practice Exercises
Engage with a variety of exercises that cover different topics. By practicing consistently, you’ll quickly spot the areas where you struggle. Repeatedly attempting problems that challenge you can help you identify gaps in your understanding and give you the chance to address them before an assessment.
Analyze Feedback and Mistakes
If you’re working with a tutor, teacher, or online platform, make sure to review feedback carefully. Pay attention to the areas where you’ve made errors and ask for clarification if something isn’t clear. Analyzing mistakes will help you understand why a solution didn’t work, allowing you to avoid repeating the same errors in the future.
Tip: If you have access to detailed solutions, review them thoroughly to see where your approach may have diverged from the correct method. This analysis can be a powerful tool for refining your skills.