AP Calculus BC Practice Exam with Answers and Solutions

Preparing for a challenging academic assessment requires a deep understanding of key concepts and the ability to apply them efficiently under time constraints. As you approach the final stages of your preparation, it’s crucial to engage with materials that allow you to test your knowledge, identify weaknesses, and build confidence. This section provides the opportunity to refine your skills through carefully structured content, designed to simulate the real test environment.

Developing a solid foundation in mathematical principles, including integration, differentiation, and related topics, will empower you to solve complex problems. Engaging with various questions will help you become familiar with the question types and improve your problem-solving techniques.

By working through sample problems and reviewing solutions, you will not only reinforce your understanding but also gain insight into the most effective methods for approaching difficult challenges. This process is essential for achieving top performance and ensuring that you’re fully prepared when it matters most.

AP Calculus BC Practice Exam with Answers

To excel in advanced mathematics assessments, it’s essential to engage with a variety of challenges that simulate real test conditions. This section provides you with a comprehensive set of problems designed to help you evaluate your knowledge and sharpen your problem-solving abilities. By working through these questions, you can build confidence and refine your approach, ensuring you’re fully prepared for the actual test.

How to Approach the Problems

Understanding the structure and style of the questions is crucial for success. These problems cover a broad range of mathematical concepts and will require you to apply different strategies. Here are a few tips for tackling the problems:

Identify the key concepts involved in each question.
Break down complex problems into smaller, manageable parts.
Use efficient methods to solve each problem, such as simplifying equations or applying known formulas.
Review your solutions and identify any errors or areas for improvement.

Reviewing the Solutions

Once you’ve completed the set, it’s crucial to review the solutions carefully. This step will help you understand the reasoning behind each answer and strengthen your mathematical skills. As you examine the solutions, focus on:

Understanding the step-by-step approach used to solve each problem.
Identifying any patterns or techniques that could be applied to similar questions in the future.
Noting areas where you may need further practice or clarification.

By dedicating time to both solving the questions and reviewing the solutions, you will deepen your understanding and enhance your ability to tackle any challenge that comes your way.

What is AP Calculus BC?

AP Calculus BC is an advanced placement course and assessment designed to challenge students by covering a wide array of mathematical topics. It builds on concepts learned in earlier studies and introduces more complex theories and applications, preparing students for college-level mathematics. The course emphasizes not only understanding fundamental principles but also applying them in various real-world scenarios and abstract problems.

The curriculum of this course covers various areas such as limits, derivatives, integrals, and series, among other topics. It is aimed at students who wish to delve deeper into mathematical theories and prepare for higher education or future careers in fields requiring advanced quantitative skills.

Topic	Description
Limits	Understanding the behavior of functions as they approach certain points.
Derivatives	Techniques to find the rate of change of a function.
Integrals	Methods for calculating areas under curves and accumulation functions.
Series	Exploration of infinite sums and their convergence.
Parametric Equations	Representation of curves and motion using parameters.

Successful completion of the course can lead to college credit, depending on the final assessment score, providing students with a head start in their academic journey. Mastery of these topics opens up opportunities for deeper studies in mathematics and its applications in science, engineering, economics, and more.

Key Topics Covered in AP Calculus BC

In this advanced course, students explore a variety of fundamental and complex mathematical concepts. These topics form the backbone of the subject and provide students with the tools to solve real-world problems and theoretical challenges. Understanding these areas is crucial for success and further study in mathematics, science, and engineering.

Fundamental Principles and Theorems

The course begins by building a strong foundation in key mathematical principles. These include:

Limits: Studying how functions behave near specific points, especially when values approach infinity or discontinuities.
Derivatives: Understanding how to calculate rates of change and applying these methods to a variety of problems.
Integrals: Mastering techniques for calculating areas under curves and solving problems involving accumulation.

Advanced Topics and Applications

As the course progresses, students delve into more advanced concepts that require deeper understanding and problem-solving ability:

Series and Sequences: Exploring infinite sums and their convergence, crucial for many applications in physics and engineering.
Polar Coordinates and Parametric Equations: Introducing alternative methods to represent curves and study motion.
Vector Calculus: Analyzing multi-dimensional motion and the application of calculus to fields like electromagnetism.

These topics are essential for building advanced problem-solving skills and preparing students for higher-level academic work. Mastery of these concepts will not only help students excel in assessments but also provide the mathematical foundation for future studies in various disciplines.

How to Approach the AP Calculus Exam

When preparing for a high-level mathematical assessment, having a clear strategy can make a significant difference. Approaching the test methodically ensures that you utilize your time effectively and tackle each problem with confidence. Success in these types of challenges requires both deep understanding and the ability to think critically under time pressure.

Effective Time Management

Managing time during the test is one of the most important factors for success. Here are a few strategies to help you allocate time efficiently:

Read through all questions before starting to solve them to get an overview of the tasks.
Start with the questions you are most comfortable with to build confidence and save time.
Allocate a specific amount of time for each section and stick to it, ensuring you have time to address every part of the test.

Understanding Question Types

Each section of the test will include different types of problems, ranging from multiple-choice to free-response questions. Familiarity with the format will allow you to approach each question more efficiently:

For multiple-choice questions, focus on eliminating incorrect options to increase your chances of choosing the right one.
For open-ended problems, break them down into smaller steps and approach them systematically, showing all necessary work.
Use diagrams or graphs where appropriate to visualize problems and simplify complex concepts.

By incorporating these strategies, you can approach the assessment with a structured plan, maximizing your performance and minimizing unnecessary stress.

Time Management Tips for AP Exams

Effective time management during a high-stakes assessment can greatly enhance performance. With a well-planned approach, you can ensure that every minute is spent wisely, allowing you to tackle all questions confidently. Organizing your time is key to completing the test successfully and reducing stress.

Prioritize and Plan

Before diving into the questions, take a moment to assess the entire test. This initial step allows you to make informed decisions on how to approach each section:

Read Through the Entire Test: Skim through all the questions first to get an overview and identify sections you feel most confident in.
Allocate Time for Each Section: Divide your available time based on the difficulty and length of each part. Allocate extra time for challenging sections or complex problems.
Set Personal Deadlines: For each question or task, set a mental deadline. This helps ensure you stay on track and don’t spend too much time on one question.

Maintain Focus and Flexibility

While sticking to a plan is important, it’s equally necessary to stay adaptable:

Don’t Get Stuck: If a particular question is taking too long, move on to the next one. Come back to difficult questions later if time permits.
Use Time Wisely: For multiple-choice questions, use the process of elimination quickly. For free-response, write out clear steps to show your understanding.
Monitor Your Progress: Regularly check the clock to ensure you’re pacing yourself well throughout the assessment.

By following these time management strategies, you can approach the test with confidence, ensuring that you complete all sections while minimizing stress.

Understanding the Multiple-Choice Questions

Multiple-choice questions are designed to test your ability to quickly and accurately assess a problem and choose the most appropriate solution from a set of options. These questions often require you to understand core principles, apply formulas, and identify patterns efficiently. By mastering the approach to these types of problems, you can improve both speed and accuracy during the assessment.

To succeed with multiple-choice questions, it’s essential to use strategies that enhance your decision-making process. Below are some key techniques to keep in mind:

Strategies for Answering Multiple-Choice Questions

Read Carefully: Always read the question and all the provided options thoroughly. Pay attention to details and nuances that might differentiate the correct answer from the others.
Eliminate Obvious Distractions: If you spot answers that are clearly incorrect, cross them out immediately. This increases your chances of selecting the right option.
Look for Clues: Many times, the wording of the question or other options can give you hints about the correct answer. Look for keywords or terms that align with concepts you’re familiar with.
Work Backwards: If you’re unsure, try plugging each answer option into the equation or scenario to see which one fits best.

Dealing with Difficult Questions

If you encounter a particularly challenging multiple-choice question, don’t panic. Instead, use the following methods:

Skip and Return: If a question is taking too long, mark it and move on. You can come back to it later with a clearer mind or after solving easier questions.
Guess Strategically: If you need to guess, eliminate as many incorrect answers as possible and make an educated guess from the remaining options.
Check for Consistency: If two options seem similar but differ slightly, consider the possibility of one being a more refined or accurate version of the other.

By using these strategies, you can navigate through multiple-choice questions more effectively, improving your overall performance and increasing your chances of selecting the correct answer. Remember, practice and familiarity with these techniques are key to mastering this type of problem.

How to Solve Free Response Questions

Free response questions assess your ability to solve complex problems in detail, requiring not only correct answers but also the steps you took to arrive at them. These problems often involve multiple stages and test your deep understanding of mathematical concepts. Solving these questions successfully requires a structured approach, careful planning, and clear reasoning.

When tackling free response questions, it’s essential to break down each problem into manageable steps and communicate your reasoning effectively. Below are key strategies to help you approach these problems systematically:

Step-by-Step Problem Solving

Start by identifying what the question is asking and outline your plan of action. Follow these steps to stay organized:

Read the Problem Carefully: Ensure you fully understand what is being asked. Look for key terms, operations, and any conditions that are given.
Break It Down: Break the problem into smaller, more manageable parts. If the question involves multiple steps, tackle one part at a time.
Use Appropriate Formulas: Choose the correct methods or formulas based on the information provided. Be sure to apply them accurately.
Show All Work: Clearly write out each step of your solution. Even if the answer is correct, partial credit can be awarded for demonstrating the right process.
Check Your Work: After completing each part, check your solution for errors and verify that it addresses the original question.

Organizing Your Solution

Presenting your solution clearly can make a significant difference in how it is graded. A well-organized response helps you stay on track and ensures that your reasoning is easily understood. Follow this format:

Step	Action
1	Write down the known values and what you need to find.
2	Set up any necessary equations or relationships between variables.
3	Carry out calculations step by step, showing every intermediate result.
4	Clearly label the final answer and ensure it’s in the correct units, if applicable.

By following these steps, you will improve your ability to solve free response problems effectively and present your solutions clearly. This methodical approach will help you maximize your score and demonstrate your problem-solving skills.

Common Mistakes to Avoid on the Exam

During high-stakes assessments, it’s easy to make avoidable mistakes that can cost you valuable points. Many of these errors are due to simple oversights or misinterpretations, rather than a lack of knowledge. Being aware of common pitfalls and taking steps to avoid them will help ensure you perform to the best of your ability.

Below are some frequent mistakes that candidates make and tips on how to steer clear of them:

Common Errors to Watch Out For

Misreading the Question: Always double-check what the question is asking. Many mistakes happen when students misinterpret the problem or overlook important details.
Rushing Through Calculations: While time is limited, speeding through calculations can lead to careless mistakes. Take your time to check each step and ensure accuracy.
Skipping Steps: Skipping intermediate steps might save time, but it can result in missing crucial points or errors in reasoning. Always show your work, even for seemingly simple tasks.
Forgetting Units or Labels: For quantitative problems, failing to include correct units or labels can result in an incomplete answer, even if the calculation is correct.
Not Reviewing Work: If time allows, review your responses before submitting. This ensures that you catch any errors or miscalculations you might have overlooked initially.

How to Prevent These Mistakes

Taking proactive steps to avoid these common errors can improve your overall performance. Below are effective strategies for preventing mistakes:

Mistake	Prevention Strategy
Misreading the Question	Carefully read the question twice, highlighting key terms and information.
Rushing Through Calculations	Work at a steady pace, double-checking calculations after each step.
Skipping Steps	Write out every step, even if the solution seems obvious, to avoid errors.
Forgetting Units or Labels	Always include appropriate units or labels when applicable and check them before finishing.
Not Reviewing Work	Set aside time at the end to review all answers and ensure everything is correct.

By being mindful of these common mistakes and implementing strategies to avoid them, you can approach the assessment with greater confidence and improve your chances of success.

Effective Study Strategies for Calculus BC

Mastering advanced mathematical concepts requires not only understanding the material but also adopting a strategic approach to studying. By focusing on the most important topics, practicing regularly, and using a variety of study methods, you can enhance your problem-solving abilities and deepen your understanding. Implementing an effective study plan is key to excelling in any rigorous assessment.

Here are some proven study strategies to help you succeed in mastering complex mathematical topics:

Start Early: Begin your preparation well in advance to give yourself plenty of time to review concepts, solve problems, and reinforce your understanding.
Break Down Complex Topics: Divide difficult concepts into smaller, more manageable sections. Focus on mastering each section before moving on to the next.
Practice Regularly: Consistent practice is essential for reinforcing concepts. Work through a variety of problems to build your skills and gain confidence in your abilities.
Use Different Resources: Explore a variety of study materials such as textbooks, online tutorials, or video lessons. Different perspectives can help clarify difficult concepts.
Teach What You Learn: Teaching a concept to someone else is one of the best ways to reinforce your understanding. Try explaining complex ideas to a study partner or even to yourself.
Focus on Weak Areas: Identify the topics or types of problems you find most challenging and dedicate extra time to improving in those areas.
Review Mistakes: When practicing, pay close attention to errors and misunderstandings. Learn from them by revisiting the material and ensuring you understand the correct process.

By adopting these strategies, you’ll create a solid foundation for your learning and approach complex topics with greater ease. Regular practice, along with a focus on mastering fundamental principles, will help you achieve success in any advanced mathematical assessment.

Utilizing Practice Tests for Success

Simulated assessments are one of the most effective tools for reinforcing knowledge and improving problem-solving skills. By working through sample questions in a test-like environment, you gain valuable experience that helps build confidence and enhances time management skills. These exercises allow you to identify your strengths and weaknesses, providing insights into areas where further focus is needed.

Here are several ways to make the most of these mock assessments:

Replicate Test Conditions: Take the mock tests under similar conditions to the actual assessment. This means limiting the time, eliminating distractions, and completing the test in one sitting. Simulating the real experience will help you become more comfortable when it matters most.
Review Mistakes: After completing each mock test, carefully review your answers, especially the incorrect ones. Understand where you went wrong and why, so you can avoid similar errors in the future.
Focus on Time Management: Practice solving questions within the time limits to develop an efficient pace. Working under pressure will help you get comfortable with managing the clock during the real test.
Track Your Progress: Keep a record of your mock test results and note improvements or recurring issues. Tracking your performance over time helps you identify patterns and gauge your readiness.
Target Weak Areas: Use the results from your simulated assessments to pinpoint topics that need additional attention. Focus your study efforts on these areas to improve your overall performance.
Vary the Difficulty Level: Don’t limit yourself to easy questions. Practice with a mix of both basic and challenging problems. This will ensure you are prepared for any difficulty level that might appear in the actual assessment.

By consistently incorporating mock tests into your study routine, you not only prepare yourself for the real experience but also refine your test-taking strategies and boost your confidence. The more you practice, the better equipped you’ll be to perform successfully.

Answer Key for AP Calculus Practice Exam

Having access to a solution guide is crucial for evaluating your performance and understanding the correct approaches to various problems. By reviewing detailed explanations for each question, you can pinpoint where you made mistakes and learn the right methods to solve similar problems in the future. The key not only confirms your answers but also helps reinforce concepts, providing deeper insights into how each solution is derived.

Below is a comprehensive breakdown of the correct responses to the problems, along with the reasoning behind each one:

Multiple Choice Questions

For the multiple-choice section, reviewing the correct options is essential. This part allows you to compare your selected answers with the correct ones and identify areas where you may have misunderstood the concepts.

Question 1: Correct Answer: B – Explanation: To solve for this, we used the fundamental theorem of calculus to integrate the given function over the specified range.
Question 2: Correct Answer: D – Explanation: This question required applying the chain rule, which was key to obtaining the correct result.
Question 3: Correct Answer: A – Explanation: The correct approach here was to use limits and determine the behavior of the function as it approached infinity.

Free Response Questions

In this section, solutions are provided with step-by-step instructions. This is where showing your work and following logical steps is essential for full credit.

Question 1: Correct Solution: Begin by differentiating the given equation, then apply the product rule to simplify the expression.
Question 2: Correct Solution: The area under the curve can be determined by setting up the proper integral, followed by solving it using integration by parts.

Reviewing these solutions and understanding the thought process behind each step will not only improve your understanding of the material but will also help you avoid making similar mistakes in the future.

Breaking Down the Practice Test Solutions

Understanding how to approach and solve each question in a mock assessment is a crucial part of mastering the material. It’s not just about getting the right answer but also understanding the reasoning behind each step. By breaking down the solutions, you can see the thought process involved in solving each problem and learn valuable techniques that will help you tackle similar questions in the future.

In this section, we’ll walk through the correct solutions, highlighting key steps and strategies to ensure a deeper understanding of the content. This will also provide clarity on any mistakes made, so you can avoid them in the future.

Multiple Choice Solutions

When working through multiple-choice questions, it is important to break down each option and understand why the correct answer is the best choice. Here’s how to approach these types of questions:

Question 1: The correct answer is option B. To solve this, we use integration by parts. By recognizing the components, we apply the appropriate formula to simplify the integral.
Question 2: The correct answer is option D. This involves using the chain rule to differentiate the composite function. Step-by-step analysis reveals that this is the most efficient approach.
Question 3: The correct answer is option A. This question tests the limit of a function at infinity, and applying L’Hopital’s Rule helps us find the correct value.

Free Response Solutions

For free-response problems, it’s essential to break down the solution into manageable parts. The key is to show every step clearly and understand why each operation is performed. Here’s a detailed walkthrough of how to approach these questions:

Question 1: First, differentiate the given equation. Then, apply the product rule to obtain the simplified expression. This step ensures we account for all components correctly.
Question 2: Set up the integral to find the area under the curve. Use integration by parts to handle the complex functions and solve it in stages.

By carefully following the steps outlined in these solutions, you can reinforce your problem-solving abilities and gain confidence in your approach. Understanding the process behind each solution ensures you’re fully prepared for any similar questions on the real test.

How to Improve Your Problem-Solving Skills

Developing strong problem-solving abilities is essential for success in any challenging subject. The key to becoming a better problem solver lies in practice, understanding concepts, and applying strategies in different contexts. By honing these skills, you can approach complex problems with confidence and precision.

Improvement in problem-solving comes from consistent effort and learning from mistakes. Here are some effective strategies to enhance your abilities:

1. Break Down the Problem

One of the most effective ways to approach a difficult problem is to break it down into smaller, manageable parts. This step-by-step approach not only helps you understand the problem better but also makes it less overwhelming. Try the following:

Identify the key components of the problem.
Understand what information is given and what is being asked.
Organize your thoughts and plan your approach.

2. Practice Different Types of Problems

Exposing yourself to a variety of problems helps you become more adaptable and sharp. The more diverse the problems you solve, the better you’ll understand the different methods and techniques used to tackle them. Incorporate these practices into your routine:

Solve problems from different topics to build a broad skill set.
Challenge yourself with increasingly difficult problems to stretch your abilities.
Review solutions to understand why specific approaches work well.

3. Learn from Mistakes

Making mistakes is a natural part of the learning process. Instead of getting discouraged, use each mistake as an opportunity to improve. Here’s how:

Analyze the errors you made and determine what went wrong.
Try to identify any patterns in the mistakes you make.
Ask for feedback and look for different methods to solve the problem correctly.

4. Develop a Strong Conceptual Foundation

To solve problems effectively, you must understand the underlying concepts. Focus on grasping the theory behind each topic before jumping into solving problems. This approach helps you apply the right strategies when faced with different scenarios.

Review key concepts regularly to strengthen your understanding.
Ask questions and seek clarification if something is unclear.
Apply concepts to real-life situations to deepen your comprehension.

By consistently practicing and refining these strategies, you’ll build the problem-solving skills needed to excel in any challenging subject. Keep working on your approach, and over time, you will notice significant improvement in your abilities.

The Role of Graphing Calculators in Calculus

Graphing calculators are invaluable tools that assist students in visualizing and solving complex mathematical problems. These devices not only simplify calculations but also allow for a deeper understanding of mathematical concepts through graphical representation. In advanced mathematics, where functions and their behaviors can be intricate, graphing calculators provide a way to explore and analyze these relationships in real time.

Utilizing these calculators effectively can enhance learning, speed up computations, and allow students to focus on problem-solving strategies rather than getting bogged down in manual calculations. Below are some key ways graphing calculators contribute to the learning process:

1. Visualizing Functions and Graphs

One of the most significant benefits of using a graphing calculator is the ability to quickly plot functions and visualize their behavior. This allows students to:

See the shape and properties of functions (e.g., symmetry, intercepts, and asymptotes).
Understand the relationship between algebraic expressions and their graphical representations.
Compare different functions by graphing them simultaneously for easy analysis.

2. Simplifying Complex Calculations

In advanced topics, computations often become cumbersome, and mistakes can be easily made when done by hand. Graphing calculators can simplify these tasks by:

Performing derivatives and integrals with ease, providing immediate results.
Solving systems of equations and inequalities that might otherwise take significant time.
Providing numerical approximations when exact solutions are difficult to compute manually.

3. Enhancing Problem-Solving Strategies

Beyond calculation, these devices help students approach problems from multiple angles. Here’s how:

They allow for experimentation with different parameters and constants in functions, helping students find patterns and solutions more intuitively.
Graphing calculators help identify potential areas where errors may occur, encouraging students to check their work in real-time.
They facilitate simulations of complex mathematical models, aiding students in solving real-world problems and scenarios.

4. Preparing for Standardized Tests

Many standardized tests allow the use of graphing calculators, making it crucial for students to be familiar with their functions. By incorporating the device into practice sessions, students can:

Become proficient in navigating the calculator’s features.
Save valuable time during exams by automating routine calculations.
Gain confidence in applying their knowledge to solve problems effectively under timed conditions.

In conclusion, graphing calculators are powerful educational tools that provide both practical advantages and deeper insights into mathematical concepts. Their role extends beyond mere computation, offering a way for students to explore, analyze, and solve mathematical problems with greater ease and efficiency.

Reviewing Integration and Differentiation Concepts

Mastering the concepts of integration and differentiation is essential for solving a wide range of mathematical problems. These two fundamental techniques are at the heart of advanced mathematics, providing the tools needed to analyze change, area, and other key properties of functions. By revisiting these concepts, students can strengthen their understanding and improve their ability to tackle more complex problems.

Understanding how to apply these methods in various contexts is crucial. While integration focuses on finding areas under curves or total accumulation, differentiation helps in determining rates of change and slopes of tangents to curves. A solid grasp of both allows students to confidently approach a variety of problems, from real-world applications to theoretical challenges.

Key Concepts in Differentiation

Differentiation deals with the concept of finding the rate of change of a function. Here are the key ideas to keep in mind when working with derivatives:

Concept	Description
Derivative of a function	Represents the rate of change of a function at a given point, or the slope of the tangent line to the curve.
Product and Quotient Rules	Used when differentiating products or quotients of two functions. The product rule is used for multiplication, while the quotient rule applies to division.
Chain Rule	Allows differentiation of composite functions, where one function is nested inside another.
Higher-order derivatives	Refers to the derivative of a derivative, providing deeper insights into the curvature and concavity of the function.

Key Concepts in Integration

Integration focuses on finding the accumulated area under a curve or the total accumulation of a quantity. The key concepts in integration include:

Concept	Description
Indefinite Integrals	Represents the general form of an antiderivative, providing a family of functions that could have produced the given rate of change.
Definite Integrals	Used to calculate the total area under a curve between two specific points, giving a numerical result rather than a family of functions.
Fundamental Theorem of Calculus	Links the concept of differentiation and integration, showing that differentiation and integration are essentially inverse operations.
Integration by Parts	A method used to solve integrals involving the product of two functions, based on the product rule for differentiation.
Substitution Method	A technique used to simplify integrals by substituting part of the function with a new variable, making the integration process easier.

By revisiting these concepts and applying them in different contexts, students can develop a deeper understanding of how functions behave and how to solve problems that involve rates of change or areas. Practicing a variety of problems using these methods will reinforce their skills and improve their confidence in handling more challenging topics.

Test-Taking Strategies for High Scores

Achieving a high score on a challenging assessment requires more than just knowledge; it also involves effective strategies that can help manage time, reduce stress, and ensure accuracy. A strategic approach can significantly improve performance, especially when facing complex problems. By preparing both mentally and physically, and using specific tactics during the test, you can maximize your potential and increase your chances of success.

Here are some essential strategies that can help you perform at your best:

Pre-Test Preparation

Organize Your Study Time: Create a study schedule leading up to the test. Prioritize weak areas while also revisiting strong topics to maintain balance.
Understand the Format: Familiarize yourself with the structure and types of questions that will appear. This will help you feel more confident and reduce surprises on test day.
Get Adequate Rest: A well-rested mind performs better. Avoid last-minute cramming and ensure you get a good night’s sleep before the test.

During the Test

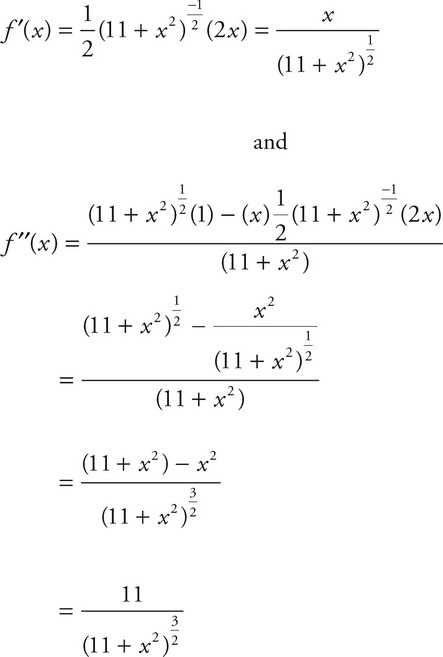
Time Management: Allocate time to each section or question based on its complexity. Keep track of time and make sure to pace yourself to avoid rushing at the end.
Read Instructions Carefully: Skim through the instructions and any question-specific details. Missing important information can lead to avoidable mistakes.
Start with What You Know: Tackle questions you feel confident about first. This will help build momentum and ensure you secure easy points early on.
Don’t Get Stuck: If you encounter a difficult question, move on and come back to it later. Spending too much time on a single question can cost valuable time.
Show Your Work: For questions that require detailed solutions, write down your thought process. This can help you stay organized and may also earn you partial credit even if the final answer is incorrect.

After the Test

Review Your Responses: If time allows, double-check your answers to ensure there are no mistakes, especially in calculations or misunderstood questions.
Stay Calm: It’s easy to worry about difficult questions, but remember that one tough problem doesn’t define your overall performance. Stay calm and trust in your preparation.

Implementing these strategies will not only help you manage your time effectively but also approach the test with confidence and clarity. By practicing these techniques and maintaining a positive mindset, you’ll be better equipped to perform at your best and secure high marks.

What to Expect on the Actual AP Exam

When preparing for a high-stakes assessment, it’s crucial to understand what to expect on the test day. Knowing the structure, the types of questions, and the testing environment can help reduce anxiety and allow you to perform at your best. The format of the test is designed to challenge your problem-solving abilities, critical thinking, and time management skills, so being familiar with what lies ahead will give you an edge.

Here’s what you can expect during the actual test:

Test Structure

Two Main Sections: The test typically consists of two major parts: multiple-choice questions and free-response questions. Both sections assess your ability to apply knowledge in various contexts, though they differ in format and style.
Multiple-Choice Questions: This section will present a series of problems, each with four possible answers. You’ll need to identify the correct solution based on the problem’s requirements. This part tests your ability to quickly apply concepts and make informed choices.
Free-Response Questions: These questions require you to solve problems in greater detail. You will need to show your work, explain your reasoning, and provide clear solutions. These questions are designed to evaluate your depth of understanding and problem-solving approach.

Time Constraints

Limited Time Per Section: Each part of the test has a specific time limit. The multiple-choice section generally allows you less time per question, while the free-response section gives you more time to work through each problem. Managing your time wisely will be essential to completing both sections within the allotted time frame.
Time Management is Key: You may need to pace yourself during the test to ensure you have enough time for all questions. If you get stuck on a question, it’s often best to move on and return to it later, rather than losing valuable time.

Testing Environment

Controlled Setting: The test will be administered in a quiet, controlled environment, typically in a classroom or large hall. You will be seated at a desk with your materials (pencil, calculator, etc.) and will be monitored by proctors to ensure fair testing conditions.
Prohibited Items: Items such as cell phones, notes, and electronic devices (other than approved calculators) are not allowed in the testing area. Make sure to review the testing rules beforehand to avoid any confusion on the day of the test.

Overall, while the assessment is designed to be challenging, knowing what to expect can help you feel more confident and prepared. Understanding the structure, time limits, and environment will allow you to focus on demonstrating your skills to the best of your ability. Make sure to approach the test with a calm and focused mindset to maximize your performance.

Post-Exam Tips for Continuous Learning

Once you have completed a high-stakes assessment, the journey doesn’t end there. It’s important to continue building on your knowledge and skills, whether you’ve done well or encountered difficulties. Post-assessment reflection and strategic follow-up are essential for deepening your understanding and improving in the long term. Here are a few tips to help you stay on track and continue learning after the test.

Review Your Performance

Analyze Mistakes: Take the time to go over the questions you found challenging. Understand where you made mistakes and identify areas for improvement. Did you misinterpret a question? Did you rush through a section? Reflecting on your approach will help you refine your problem-solving strategies for future challenges.
Review Correct Answers: It’s just as important to review the questions you got right. Think about why those answers were correct and how you arrived at them. This will reinforce your knowledge and boost your confidence for the next time you encounter similar problems.

Continue Practicing and Learning

Use Additional Resources: Keep learning by using various study materials, such as textbooks, online resources, and video tutorials. Exploring different perspectives will help you solidify concepts and fill in any gaps in your understanding.
Set New Learning Goals: Reflect on areas you still find difficult or topics that were not covered extensively. Set specific, measurable goals to improve those skills. This will ensure that you’re making steady progress and advancing your overall competence in the subject.
Challenge Yourself: Don’t shy away from more difficult problems. Practice tackling more complex scenarios and explore higher-level concepts. Gradually, this will help you develop a deeper understanding and greater mastery of the material.

Continuous learning is key to long-term success. Whether you felt confident or faced challenges during the assessment, the post-test period is an opportunity to strengthen your abilities. By reviewing your performance, setting goals, and consistently practicing, you’ll continue to improve and be well-prepared for future opportunities.