
In this section, we delve into a comprehensive review of essential problems encountered in the AP math assessment. This part focuses on fundamental concepts and methods that are critical for achieving success in the test. Students will find solutions to various problems, providing clarity and understanding for each step in the process.
By analyzing key techniques and mathematical principles, this guide helps enhance your ability to solve complex questions effectively. Emphasis is placed on applying theoretical knowledge to practical scenarios, allowing for a better grasp of the material and preparation for the upcoming challenges.
Whether you’re working through challenging questions or refining your problem-solving skills, this resource offers detailed explanations to ensure mastery of the core concepts. With a mix of critical reasoning and strategic approaches, you will be well-equipped to tackle similar problems in future assessments.
AP Mathematics Test Problem Solutions
This section provides a detailed breakdown of key problems often encountered in the AP math assessment. It is designed to guide students through common challenges, focusing on the essential principles and methods required to solve each problem effectively. The solutions are presented step-by-step, allowing for a clear understanding of the problem-solving process.
Through examining various types of problems, the goal is to equip students with the necessary skills to approach complex scenarios with confidence. By breaking down each question, we highlight important strategies and techniques that can be applied to similar problems in future assessments. Mastery of these concepts is crucial for performing well under exam conditions.
Each solution emphasizes critical thinking and logical reasoning, ensuring that students are not only able to arrive at the correct results but also understand the underlying concepts. This approach helps build a solid foundation for tackling higher-level mathematical problems, enhancing both accuracy and efficiency in solving them. Practice and familiarity with these types of questions are key to success in any mathematical evaluation.
Overview of AP Mathematics Test Format
The AP mathematics assessment is structured to evaluate a student’s understanding of key mathematical concepts and their ability to apply these concepts in problem-solving scenarios. The test is designed to challenge students’ critical thinking skills, covering a range of topics from functions to limits and derivatives. The structure ensures that students can demonstrate both theoretical knowledge and practical application.
Test Structure and Timing
The evaluation consists of multiple-choice questions and free-response problems, each testing different aspects of the curriculum. Students are given a limited amount of time to complete each part, requiring both accuracy and speed. The test is divided into two sections, with each section designed to assess specific skills. The first part typically includes multiple-choice questions, while the second part focuses on free-response problems, allowing for deeper exploration of individual topics.
Key Areas of Focus
Throughout the test, emphasis is placed on the application of mathematical methods to real-world situations. Questions range from basic calculations to more complex problems requiring a deeper understanding of mathematical principles. A strong foundation in problem-solving strategies is essential for success, as students must demonstrate the ability to navigate through various problem types efficiently. Mastery of fundamental topics is critical for performing well in this assessment.
Understanding the Test Structure
This part of the assessment is designed to evaluate your ability to apply mathematical principles and solve problems under timed conditions. The structure is focused on testing both your theoretical knowledge and practical problem-solving skills. Questions are crafted to assess your understanding of key topics, requiring a clear approach and precise calculations.
Types of Questions
The questions in this section are primarily multiple-choice, each presenting a set of possible answers. You will need to choose the correct option based on your understanding of the material. These questions test your ability to quickly recognize patterns and apply appropriate formulas or methods. Critical thinking is required to select the best answer in a limited time frame.
Skills Tested
This section focuses on your ability to manipulate mathematical concepts and apply them to real-world scenarios. You will encounter problems related to limits, derivatives, and function behavior, among others. Efficiently navigating through these questions requires not only a solid understanding of the material but also the ability to manage time effectively, ensuring all questions are addressed within the given period.
Key Topics Covered in Part A
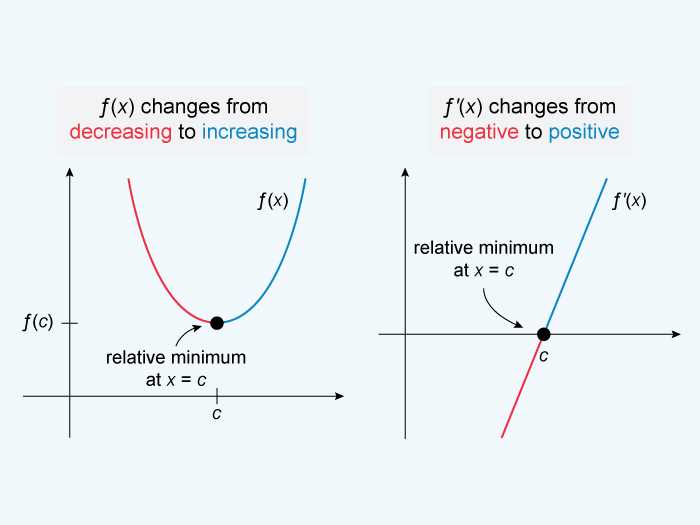
This segment of the assessment highlights several fundamental concepts that are essential for understanding advanced mathematical problem-solving. The questions focus on testing your ability to apply core principles, such as rates of change, behavior of functions, and limits. A solid grasp of these topics is crucial for navigating the problems effectively and accurately.
Limits and Continuity
Understanding limits is one of the foundational topics covered. Questions often explore how functions behave near specific values, testing your ability to evaluate limits and identify points of discontinuity. Mastery of this topic allows you to determine function behavior at critical points, a key skill for solving more complex problems in later stages.
Rates of Change and Derivatives
The ability to compute and interpret rates of change is another central focus. Problems in this area often involve finding derivatives to determine how functions change over time or with respect to other variables. Calculating derivatives and understanding their geometric significance are essential for successfully answering these types of questions.
Function Analysis
In addition to limits and derivatives, this section tests your skills in analyzing different types of functions. Whether it’s linear, exponential, or logarithmic, questions challenge your ability to recognize function behavior and apply appropriate methods for solving related problems. This broad knowledge is key to answering questions that involve optimization, curve sketching, and other advanced techniques.
How to Approach Multiple-Choice Questions
Multiple-choice questions can often seem challenging, but with the right approach, you can navigate them efficiently. The key is to focus on both your understanding of the material and the strategies you use when tackling each problem. Here are some steps to help you improve your performance:
- Read the question carefully – Make sure you understand what is being asked before you look at the options. Pay attention to keywords like “maximum,” “minimum,” “increasing,” and “decreasing” that help define the problem.
- Eliminate obvious incorrect choices – Even before calculating, quickly rule out any answers that are clearly wrong. This increases your chances of selecting the correct one.
- Work through the problem step-by-step – If possible, solve the problem on scratch paper or in your head before reviewing the answer choices. This ensures that your reasoning matches the options provided.
- Look for patterns in the choices – If the options contain numbers that seem out of place or too extreme, they may be incorrect. This can help you narrow down the possibilities.
- Check for negative signs or special conditions – Pay close attention to signs in equations or specific conditions stated in the problem. Misreading these details can easily lead to mistakes.
- Manage your time effectively – Don’t spend too much time on any one question. If you’re stuck, make an educated guess and move on. You can always come back later if time allows.
By applying these strategies, you’ll improve your chances of selecting the right answer and manage your time more effectively during the test.
Common Mistakes in Part A Responses
When approaching this part of the assessment, students often make certain errors that can cost them valuable points. These mistakes generally arise from misunderstandings of key concepts, miscalculations, or simply overlooking details in the problem. By identifying and addressing these common pitfalls, you can improve your accuracy and increase your overall score.
Misinterpreting the Problem
One of the most frequent mistakes is misinterpreting the wording of the question. Even a small detail can change the direction of your solution. Here are some common issues:
- Missing important conditions – Always pay attention to specific conditions mentioned, such as limits, continuity, or function restrictions.
- Confusing terminology – Terms like “rate of change” or “local maximum” are precise and should be interpreted correctly to avoid solving the wrong type of problem.
- Overlooking units or signs – Ignoring units of measurement or signs (positive or negative) can lead to incorrect conclusions.
Calculation Errors
Even if the problem is understood correctly, errors in the calculation process are common. Here are some areas where mistakes often occur:
- Incorrect application of formulas – Using the wrong formula or applying it incorrectly can result in wrong answers. Always verify that the formula is appropriate for the problem at hand.
- Sign mistakes – One of the most common errors is making sign errors during calculations, especially when dealing with derivatives or integrals.
- Rounding too early – Rounding off intermediate steps can cause a loss of precision. It’s better to keep values as exact as possible until the final answer.
By being mindful of these common mistakes, you can approach the questions with greater confidence and precision, leading to more accurate results on your test.
Strategies for Efficient Time Management
Time management is a critical skill when tackling any timed assessment. Being able to pace yourself effectively ensures that you can answer all questions thoughtfully without feeling rushed. It’s not just about working quickly; it’s about working smart. By adopting the right strategies, you can maximize your performance and reduce stress during the test.
Prioritize and Plan
Before diving into the problems, take a moment to scan through the entire set of questions. Identify the ones that you find easier or are more familiar with, and tackle those first. This will help you build confidence and ensure that you score points on questions you can easily answer. For more challenging problems, allocate extra time later, once the quicker ones are out of the way.
- Start with easier problems – Answering straightforward questions quickly boosts your confidence and saves time.
- Skip and return – If a question is too difficult, move on and come back to it later. This avoids wasting time on one problem when there are others to solve.
- Set time limits – Give yourself a specific amount of time for each question. This will help prevent spending too long on any single item.
Stay Focused and Avoid Overthinking
Overthinking a problem can lead to unnecessary mistakes and lost time. It’s important to stay focused on what is being asked and to avoid second-guessing your initial thoughts. Trust your instincts and the methods you’ve practiced. If a problem doesn’t immediately make sense, move on and return to it later with a fresh perspective.
- Stick to your first choice – Often, the first answer that comes to mind is correct. Don’t waste time doubting your choices.
- Break down complex problems – If a question seems overwhelming, break it down into smaller, manageable parts. Solving each part step-by-step is often more efficient.
- Keep an eye on the clock – Regularly check the time to ensure you’re on track to complete all questions.
By applying these strategies, you’ll be able to approach your test with greater efficiency, ensuring you complete all problems while maintaining accuracy and clarity in your work.
Solving Limits and Derivatives Problems
In many assessments, solving problems related to changes in functions and their behavior is essential. These types of questions typically focus on understanding the limits of a function as it approaches certain values and determining the rate of change through derivatives. A methodical approach to solving these problems can greatly improve accuracy and efficiency.
Approaching Limit Problems
When solving limit-related questions, it’s important to first check if direct substitution works. If it doesn’t, you may need to apply algebraic manipulation, such as factoring or rationalizing, to simplify the expression. In some cases, you may also encounter special limits such as indeterminate forms or infinite limits, which require more advanced techniques.
Working with Derivatives
To solve derivative problems, begin by recalling key rules such as the power rule, product rule, and chain rule. Each rule serves a specific purpose for differentiating different types of expressions. Identifying which rule to use based on the structure of the function is critical for arriving at the correct derivative.
| Function Type | Rule to Use |
|---|---|
| Polynomial Functions | Power Rule |
| Product of Two Functions | Product Rule |
| Composite Functions | Chain Rule |
By mastering these fundamental techniques, you will be able to solve limits and derivatives problems with confidence and precision. The key is to practice each step carefully and develop an intuitive understanding of when and how to apply each rule.
Analyzing Function Behavior in Part A
In this section of the assessment, understanding the behavior of functions plays a crucial role in solving problems effectively. The ability to analyze key features such as continuity, intervals of increase or decrease, and local extrema is essential for interpreting the function’s overall shape and characteristics. This section requires a strategic approach to recognize patterns and apply the appropriate methods to analyze different types of functions.
Identifying Critical Points
Critical points are where the function’s behavior changes. These points occur where the derivative is zero or undefined. Identifying these points allows you to determine important characteristics, such as maxima, minima, or points of inflection.
- Find the derivative – Start by taking the derivative of the function to locate where it equals zero or is undefined.
- Test intervals – Once you have critical points, test intervals between them to determine if the function is increasing or decreasing.
- Classify critical points – Use the first or second derivative test to classify the critical points as local maxima, minima, or points of inflection.
Determining Limits and Asymptotic Behavior
Another critical aspect of analyzing a function is determining its behavior as it approaches certain values or infinity. This can provide insights into the function’s long-term trends and possible asymptotes.
- Find one-sided limits – Check how the function behaves as it approaches specific points from either side.
- Evaluate infinite limits – Analyze how the function behaves as the input grows very large or very small, potentially leading to vertical or horizontal asymptotes.
- Consider end behavior – For rational functions, determine the end behavior by examining the degrees of the numerator and denominator.
By mastering these techniques, you can analyze the behavior of any function and apply this knowledge to solve problems more accurately in the test.
How to Interpret Graphical Questions
Graphical questions in assessments often require you to analyze visual representations of functions or data to extract key information. These types of problems test your ability to translate what you see into mathematical concepts, such as understanding slopes, intercepts, and areas under curves. Interpreting these graphs correctly is essential for making informed decisions and solving problems efficiently.
Identifying Key Features on a Graph
When presented with a graph, the first step is to identify important features that can guide you in solving the problem. These might include the function’s intercepts, maxima, minima, asymptotes, and inflection points.
- Intercepts – Look for where the graph crosses the x-axis (x-intercepts) and y-axis (y-intercepts). These values are often critical for solving equations or understanding behavior.
- Extrema – Identify the highest or lowest points on the graph, which indicate local maxima or minima. These points provide insight into the function’s overall behavior.
- Asymptotes – Pay attention to any lines the graph approaches but never reaches, indicating horizontal, vertical, or oblique asymptotes.
Analyzing Slopes and Rates of Change
Another important aspect of interpreting graphs is understanding the slope of a function at various points. The slope of a graph at a specific point corresponds to the rate of change of the function at that point, which is often the focus of the question.
- Positive and Negative Slopes – A positive slope indicates the function is increasing, while a negative slope shows it is decreasing.
- Zero Slope – A slope of zero indicates a horizontal tangent line, which can represent a local maximum, minimum, or point of inflection.
- Increasing and Decreasing Intervals – Pay attention to intervals where the function is increasing or decreasing, as these intervals are key to understanding the graph’s behavior.
By carefully analyzing the graph’s features and understanding how they relate to the function’s properties, you can solve graphical questions more effectively and accurately.
Answering Rate of Change Questions
Rate of change questions are designed to test your ability to determine how one quantity changes relative to another. These types of problems typically involve interpreting the behavior of a function in terms of its slope or derivative. Understanding how to approach these questions requires familiarity with how rates of change describe the relationship between variables and the application of mathematical concepts to analyze these relationships effectively.
The key to answering rate of change questions is to recognize what is being asked: whether the problem is asking for the instantaneous rate at a specific point, or the average rate over an interval. In many cases, these problems can be solved by applying the definition of a derivative or using a simple difference quotient.
Here are some steps to follow when approaching these types of questions:
- Identify the function – Look at the problem to determine the function that describes the relationship between the variables.
- Find the rate of change – If the question asks for the rate at a specific point, compute the derivative of the function. If the question is asking for the average rate, use the formula for average rate of change.
- Substitute the values – Plug in the appropriate values of the variables (such as time or distance) to calculate the rate of change at the given point or over the interval.
- Interpret the result – Once you have the rate of change, interpret its meaning in the context of the problem. For example, if the rate represents speed, the result would indicate how fast an object is moving at that instant or over a given time period.
By following these steps, you can accurately determine the rate of change in a variety of contexts and apply these concepts to solve complex problems efficiently.
Examining Continuity and Discontinuity
Understanding the concepts of continuity and discontinuity is fundamental in analyzing the behavior of functions. These concepts describe whether a function behaves smoothly without interruption or whether there are sudden jumps, breaks, or undefined points in its graph. Recognizing these features allows you to identify where a function may fail to be continuous and to understand the implications of such behavior for solving problems.
Continuity refers to the idea that a function has no breaks, holes, or jumps at a particular point or over an interval. A function is considered continuous at a point if the following conditions are met:
- The function is defined at that point.
- The limit of the function as it approaches that point exists.
- The limit of the function as it approaches that point equals the function’s value at that point.
On the other hand, discontinuity occurs when any of these conditions are violated. Discontinuities can take several forms, including removable, jump, and infinite discontinuities. Understanding the different types of discontinuities is essential for accurately interpreting functions.
Types of Discontinuity
- Removable Discontinuity – This occurs when a function has a hole at a point. The limit of the function at that point exists, but the function’s value does not match the limit.
- Jump Discontinuity – This type of discontinuity happens when there is a sudden jump in the function’s value as it approaches a particular point from either direction.
- Infinite Discontinuity – This occurs when the function approaches infinity or negative infinity as it nears a certain point, often represented by vertical asymptotes.
By carefully analyzing these behaviors, you can determine whether a function is continuous or where it might exhibit discontinuities, which is crucial for solving various mathematical problems and understanding the function’s overall behavior.
Reviewing Key Theorems for Part A
Mastering key theorems is essential for solving complex mathematical problems, especially when analyzing functions. These fundamental principles provide the necessary tools for solving limits, derivatives, and other important concepts. A solid understanding of these theorems enables you to navigate challenges more efficiently and accurately, particularly in problem-solving scenarios that require deeper analysis of function behavior.
Several theorems are crucial when tackling questions related to function analysis, limits, and rates of change. By reviewing and applying these theorems, you can simplify complex problems and ensure accurate results. Below are some of the core theorems to keep in mind:
The Intermediate Value Theorem
The Intermediate Value Theorem states that if a continuous function takes on two values at any two points, it must also take on any value between those two points. This principle is particularly useful when trying to prove the existence of a solution within a given interval. For example, if a function has opposite signs at the endpoints of an interval, there is a point within that interval where the function equals zero.
The Mean Value Theorem
The Mean Value Theorem establishes that for a continuous function on a closed interval, there exists at least one point where the derivative of the function equals the average rate of change over that interval. This theorem helps in understanding how a function behaves between two points and is foundational in solving many rate-of-change problems.
By revisiting these key theorems and understanding their applications, you can approach problems in a more structured and confident manner. Each theorem offers a powerful tool that enhances your problem-solving capabilities, especially when dealing with complex mathematical expressions.
Using Derivatives to Solve Word Problems
Derivatives are powerful tools for solving real-world problems where the rate of change is important. Word problems often present situations where quantities change over time or in relation to other variables. By translating these scenarios into mathematical expressions, you can use derivatives to find critical information, such as rates of change, maximum and minimum values, or points of intersection. Understanding how to apply derivatives in these contexts can simplify complex problems and provide clear, actionable solutions.
When solving word problems, it’s essential to carefully interpret the situation described and set up equations that model the problem accurately. Once the relationship is defined, derivatives can help analyze how the system behaves, revealing insights into the changing quantities and their relationships.
Example: Rate of Change in Distance
Consider a problem where you are asked to find the speed of a car at a specific moment in time. Given a function that represents the distance traveled over time, the derivative of that function will give you the velocity of the car at any point. To solve such problems, follow these steps:
- Write the function that models the situation, e.g., d(t) = 3t^2 + 2t, where d(t) represents distance and t represents time.
- Find the derivative of the function, d'(t) = 6t + 2, which gives the rate of change of distance with respect to time (velocity).
- Substitute the given time into the derivative to find the instantaneous velocity at that moment.
Example: Maximizing Revenue
Another common application is using derivatives to maximize or minimize quantities, such as revenue or profit. Suppose you are given a function for revenue and need to determine the point at which revenue is maximized. By taking the derivative of the revenue function and setting it equal to zero, you can find the critical points. Analyzing the second derivative will confirm whether those points represent maxima or minima.
Using derivatives in word problems requires practice in interpreting the situation and translating it into mathematical terms. Once the relationship is defined, the derivative offers a systematic way to analyze the behavior of the quantities involved and find optimal solutions or rates of change. With this approach, you can tackle a wide range of real-life problems efficiently and effectively.
Applying L’Hopital’s Rule in Part A
When faced with indeterminate forms such as 0/0 or ∞/∞ in limit problems, L’Hopital’s Rule provides a systematic method to resolve these expressions. This rule allows you to differentiate the numerator and denominator separately and then re-evaluate the limit. It is a valuable tool for simplifying complex limits and is often employed in problems where direct substitution leads to indeterminate results.
Before applying L’Hopital’s Rule, it is important to confirm that the limit is in one of the indeterminate forms. Once confirmed, the next step is to differentiate the numerator and denominator. This process is repeated as necessary until the limit can be resolved. The rule simplifies the computation and provides a clear path to the solution when traditional methods fail.
Steps for Applying L’Hopital’s Rule
- Step 1: Identify the indeterminate form (e.g., 0/0 or ∞/∞).
- Step 2: Differentiate the numerator and denominator separately.
- Step 3: Re-evaluate the limit using the new expressions.
- Step 4: Repeat the process if the result is still indeterminate.
- Step 5: If a determinate value is obtained, the problem is solved.
Example: Using L’Hopital’s Rule
Consider the limit expression:
lim (x → 0) (sin(x) / x)
If you substitute 0 directly, both the numerator and denominator become 0, leading to an indeterminate form. To resolve this, apply L’Hopital’s Rule:
- Differentiate the numerator: d/dx[sin(x)] = cos(x)
- Differentiate the denominator: d/dx[x] = 1
- The new limit becomes: lim (x → 0) (cos(x) / 1) = 1
Therefore, the limit of sin(x) / x as x approaches 0 is 1.
By applying L’Hopital’s Rule, the original indeterminate form is resolved efficiently. This approach is essential when solving more complicated problems in which direct substitution does not yield a solution.
Preparing for AB Part A Assessment
Effective preparation for the first portion of any advanced mathematics assessment requires a combination of strategic review and focused practice. Understanding key concepts and honing problem-solving skills are essential for success. To excel in this section, students should prioritize mastering the foundational principles that form the basis of the questions presented. Developing strong problem-solving techniques and becoming familiar with the format will ensure a confident approach during the test.
Key Topics to Review
Focus on the core areas that are regularly tested. These include:
- Limits and Continuity: Understand the behavior of functions as they approach specific values and how discontinuities affect the graph of a function.
- Rates of Change: Be able to interpret and compute rates of change in a variety of contexts, from motion problems to growth and decay models.
- Derivatives: Master the techniques for finding derivatives, both conceptually and algebraically, and apply them to real-world scenarios.
- Application of Derivatives: Familiarize yourself with problems involving optimization and motion, where derivatives are used to analyze change.
Effective Strategies for Success
Developing a systematic study routine is key to thorough preparation. Here are a few approaches to consider:
- Practice with Timed Tests: Simulate testing conditions by taking timed practice sets to build your ability to manage time and pace yourself during the real assessment.
- Focus on Weak Areas: Identify the topics that present the greatest challenges and dedicate extra time to reinforcing your understanding of these areas.
- Review Past Problems: Go over previously asked questions to become familiar with the types of problems that may appear. Analyze both correct and incorrect solutions to improve your approach.
- Clarify Key Concepts: Make sure you have a solid grasp of important theorems and techniques, as these are frequently tested and form the basis for more complex problems.
By following a focused and strategic preparation plan, students can significantly improve their confidence and ability to perform well in the first section of the assessment.
Tips for Improving Performance
To enhance your performance during any assessment, it is crucial to focus on both mental preparation and practical strategies. Proper planning, effective study habits, and adopting time-management techniques can all contribute to a better outcome. By mastering the material and refining test-taking approaches, you can tackle questions with confidence and efficiency.
Key Strategies for Success
Implementing the following strategies can greatly improve your results:
| Strategy | Description |
|---|---|
| Understand Key Concepts | Thoroughly review foundational topics, as these will help you tackle a wide variety of problems. Don’t just memorize formulas–ensure you understand their applications. |
| Practice Time Management | Set time limits when working through practice problems to simulate the pressure of the actual assessment. Develop a pace that allows you to address all questions. |
| Focus on Weak Areas | Identify areas where you struggle most and allocate extra time to these. Strengthening your weaknesses will prevent them from hindering your performance. |
| Stay Calm and Confident | Maintaining a calm, confident mindset during the assessment allows you to focus better. Practice relaxation techniques before and during the test if needed. |
| Review Mistakes | After practice sessions, thoroughly review your mistakes and understand why you made them. This helps you avoid similar errors in the future. |
Final Preparations
As the test day approaches, ensure you are mentally and physically prepared. Adequate rest and a healthy routine leading up to the test are just as important as your study efforts. Trust your preparation, and remember that a positive attitude can significantly influence your performance.
Reviewing Practice Questions and Solutions
One of the most effective ways to prepare for any assessment is by reviewing a variety of practice problems and their corresponding solutions. This helps reinforce understanding, identify patterns, and improve problem-solving skills. Going through different types of questions enables you to familiarize yourself with the format and the kinds of challenges you may encounter, while analyzing the solutions ensures you understand the steps involved in reaching the correct answer.
Steps for Effective Review
When reviewing practice problems, consider the following steps:
| Step | Action |
|---|---|
| Understand the Problem | Before jumping into solving, carefully read the question and identify the key information. This helps you focus on what is being asked and avoid unnecessary confusion. |
| Attempt to Solve Without Looking at the Solution | Try solving the problem on your own first. This gives you a chance to identify your current understanding and pinpoint areas for improvement. |
| Analyze the Solution Step by Step | Once you look at the solution, break it down step by step. Make sure you understand why each step is taken, and how it leads to the final result. |
| Note Mistakes and Learn from Them | If you made any errors, identify where you went wrong and understand the reasoning behind the correction. This prevents similar mistakes in the future. |
| Review Similar Problems | After reviewing the solution, practice similar problems to solidify your understanding and improve speed and accuracy in problem-solving. |
Benefits of Regular Review
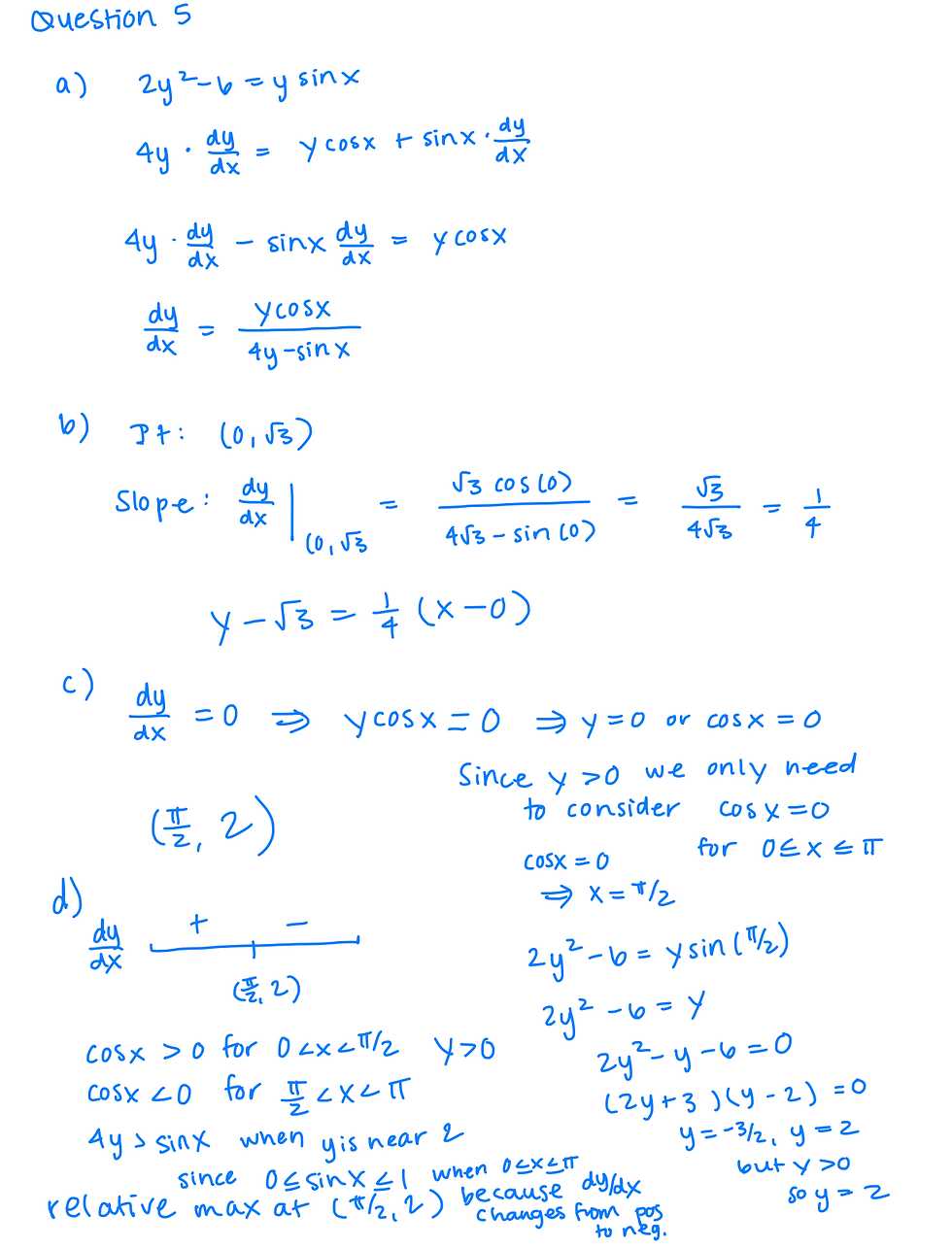
Regularly reviewing problems and their solutions helps develop a deeper understanding of the material. It also builds confidence in your ability to apply concepts and techniques effectively. The more problems you solve, the more familiar you become with the process, increasing both your proficiency and your performance on assessments.