Ap Calculus Practice Exam Answers and Solutions Guide

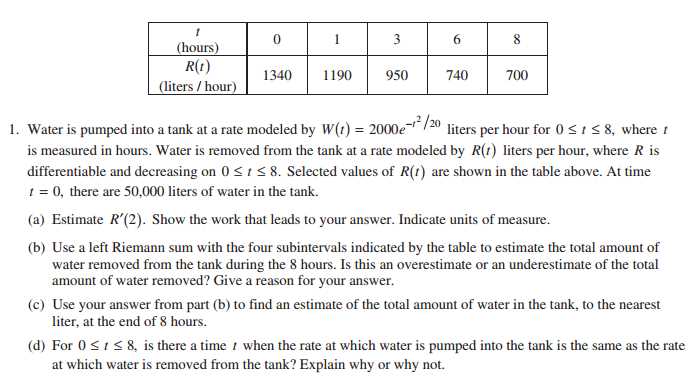
Preparing for a rigorous math assessment can be a challenging yet rewarding experience. It requires a deep understanding of key concepts and the ability to apply them in various scenarios. With the right approach and resources, you can build the confidence needed to excel in these types of evaluations.

One of the most effective ways to improve your skills is through solving relevant questions that closely mirror the actual test format. By working through problems and reviewing comprehensive solutions, you not only solidify your understanding but also learn how to approach complex problems with greater ease. Consistent practice and focused review are key to mastering the material and achieving the results you desire.

In this section, you’ll find a range of resources designed to help you hone your abilities, offering step-by-step breakdowns and expert tips to enhance your preparation. Whether you’re refining your problem-solving techniques or improving your test-taking strategies, these insights will guide you toward success.

AP Calculus Practice Exam Answers

When preparing for a high-level math test, reviewing detailed solutions is essential for mastering the material. By studying how to approach various problem types and understanding the reasoning behind each step, you can enhance your problem-solving abilities. This process not only helps reinforce theoretical knowledge but also boosts your confidence when faced with similar questions in an actual assessment.

In this section, we will provide a comprehensive breakdown of key problems, explaining each solution in a clear and systematic manner. By following these step-by-step guides, you’ll gain a deeper understanding of how to tackle challenging questions and improve your performance. Focused review and strategic practice are vital components of any effective preparation strategy.

As you work through the examples, pay attention to the methods and approaches used to arrive at the correct conclusions. These techniques are not only useful for this particular test but can also be applied to a variety of similar academic challenges.

Understanding AP Calculus Exam Format

To achieve success on a high-level mathematics assessment, it’s crucial to understand the structure and layout of the test. Familiarity with the format enables you to approach each section with confidence and better manage your time during the evaluation.

The assessment is divided into multiple sections, each designed to evaluate different aspects of your mathematical skills. Here is an overview of the key components:

Multiple Choice Section: Tests your ability to quickly and accurately solve a variety of problems.
Free Response Section: Requires you to provide detailed solutions and explain your reasoning step by step.
Time Management: Understanding how much time to allocate for each section is critical to completing the test efficiently.

By practicing under timed conditions and reviewing each section’s requirements, you’ll be better prepared to navigate the different problem types. Focusing on both the content and the structure will give you an edge during the assessment.

How to Approach Calculus Exam Questions

When faced with a challenging math test, it’s essential to have a clear strategy for tackling each problem. The key is to break down each question into manageable parts and approach it methodically. By staying organized and focused, you can navigate through complex problems with confidence.

Here are some effective techniques for addressing math problems in assessments:

Read Carefully: Make sure you understand the question fully before starting. Pay attention to details such as units, key terms, and what is being asked.
Identify What Is Given: Identify all the known information in the problem and mark it clearly. This helps you decide on the approach to solve the problem.
Choose the Right Approach: Determine the best method for solving the problem, whether it’s through algebraic manipulation, graphical analysis, or other strategies.
Work Step-by-Step: Break down the solution process into clear, logical steps. Write out every calculation to avoid mistakes.
Double-Check Your Work: Before finalizing your solution, review each step to ensure accuracy and check that your final answer makes sense in the context of the question.

By following these steps, you can improve your chances of solving problems efficiently and accurately, even under time pressure.

Common Mistakes in AP Calculus Exams

During any high-level math assessment, it’s easy to make small errors that can have a significant impact on your overall score. Recognizing and avoiding these common pitfalls is an essential part of preparation. By understanding where mistakes typically occur, you can develop strategies to avoid them and ensure more accurate results under pressure.

Below is a table highlighting some of the most frequent mistakes students make, along with tips on how to avoid them:

Error Type	Cause	How to Avoid
Misinterpreting the Question	Not reading the problem carefully or misunderstanding key terms.	Take time to fully understand what is being asked before starting your solution.
Incorrect Calculations	Careless arithmetic or algebraic mistakes during steps.	Double-check each step and use a calculator where appropriate.
Skipping Units	Forgetting to include or convert units of measurement.	Always note the units in the problem and ensure consistency throughout.
Rushing Through Solutions	Trying to complete the test too quickly, leading to sloppy work.	Take time to work through each problem, managing time efficiently to avoid mistakes.
Overlooking Simplifications	Failing to simplify answers or leaving equations in complex forms.	Always simplify expressions as much as possible, and check your final answer.

By being mindful of these common errors and taking proactive steps to avoid them, you can improve your performance and increase your chances of achieving a higher score.

Key Topics to Focus on for Success

To achieve top performance in any advanced math test, it’s essential to focus on the most critical concepts that are frequently assessed. These topics form the foundation for most problems you’ll encounter, so mastering them will significantly improve your ability to solve complex questions efficiently.

Here are some key areas that require your attention:

Limits and Continuity: Understand the behavior of functions as they approach specific points and how continuity impacts their solutions.
Derivatives and Their Applications: Be comfortable with calculating derivatives and applying them to real-world problems, such as rates of change and optimization.
Integrals: Focus on integration techniques, both definite and indefinite, and their applications in areas like area under curves and accumulation of quantities.
Applications of Derivatives: Study topics like related rates, linear approximations, and motion problems that rely on derivative concepts.
Fundamental Theorems: Make sure you understand the fundamental theorems and their role in connecting derivatives and integrals.
Series and Sequences: Practice working with infinite series and sequences, especially convergence tests and power series expansions.

By dedicating time to these critical areas, you will be well-prepared for tackling a wide range of problems with confidence. Make sure to not only practice solving problems but also to understand the underlying principles behind each topic.

Best Resources for AP Calculus Review

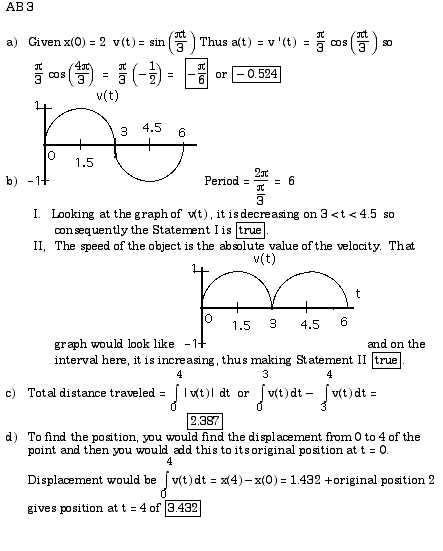
Effective preparation for any advanced mathematics test requires the right mix of materials to reinforce concepts and practice problem-solving. The best resources provide both theoretical explanations and practical exercises to ensure a well-rounded understanding of the subject.

Books and Study Guides

Comprehensive study guides and textbooks are invaluable when it comes to reviewing key concepts and strategies. These resources often break down complex topics into understandable segments and include practice questions to test your knowledge.

AP Prep Books: Publishers like Barron’s and Princeton Review offer detailed guides with practice questions and in-depth solutions.
Textbooks: Standard textbooks, such as Stewart’s “Calculus” or Larson’s “Calculus: Early Transcendental Functions,” provide thorough explanations and example problems.

Online Platforms and Tools

Digital resources make it easy to access interactive materials and simulate real test conditions. Many websites offer free tutorials, videos, and quizzes to sharpen your skills.

Khan Academy: Offers free video lessons and exercises that cover all major topics, from differentiation to integration.
College Board Resources: The official site provides practice problems, sample questions, and scoring guidelines to help you understand the format and expectations.
Wolfram Alpha: A powerful tool for checking solutions and exploring different approaches to problems.

By combining books, online platforms, and interactive tools, you can create a personalized study plan that fits your learning style and preparation needs.

Step-by-Step Solutions for Practice Tests

To fully understand complex mathematical concepts, it’s essential to go beyond just solving problems. A step-by-step approach helps you break down each question, understand the reasoning behind each move, and build confidence in your problem-solving skills. This method also ensures that you can identify where mistakes might occur and learn how to correct them.

Breaking Down the Problem

The first step in tackling any question is to thoroughly read and comprehend the problem. Once you have a clear understanding, it is important to break the problem into smaller, more manageable parts. This allows you to focus on each element individually and reduces the chance of making errors.

Identify Key Information: Extract all the important details such as given values, required outcomes, and any relevant formulas.
Choose the Right Strategy: Decide on the most effective approach–whether it’s through substitution, graphing, or solving equations directly.
Start with Known Values: Begin with the information you’re certain about, and use it to solve for unknowns step by step.

Understanding the Solution Process

Once you’ve broken down the question, it’s time to apply your solution strategy. Ensure each calculation is clearly shown, and don’t skip any steps. This not only helps avoid mistakes but also makes it easier to trace back your work if needed.

Work Through Each Step: Write out each calculation and explain your reasoning as you go. This ensures clarity and helps you identify where any errors may arise.
Double-Check Your Work: Once you have a final solution, go through the entire process again to verify that your answer is accurate and makes sense in the context of the problem.

By consistently using this step-by-step approach, you’ll be able to improve your problem-solving ability and handle even the most challenging questions with ease.

How to Analyze Practice Exam Results

After completing a series of test questions, it’s essential to reflect on your performance to identify both strengths and areas for improvement. Analyzing your results effectively can help you target specific topics that need further review and guide your preparation moving forward.

Here are some steps to follow when reviewing your test results:

Review Incorrect Answers: Go through each mistake carefully to understand why you got it wrong. Was it a simple error, or did you misunderstand the question?
Identify Patterns: Look for recurring mistakes or types of problems you consistently struggle with. This will help pinpoint areas that need more focus in future study sessions.
Check for Conceptual Gaps: If you’re consistently making mistakes in certain topics, it might indicate a lack of understanding in the underlying concepts. Take the time to review these areas more thoroughly.
Evaluate Time Management: Assess whether you spent too much time on certain questions, leaving others incomplete. This can help improve your pacing during future practice rounds.

By thoroughly analyzing your results, you can adjust your study approach to focus on weaker areas, improve your problem-solving techniques, and gain a deeper understanding of the material.

Improving Your Time Management Skills

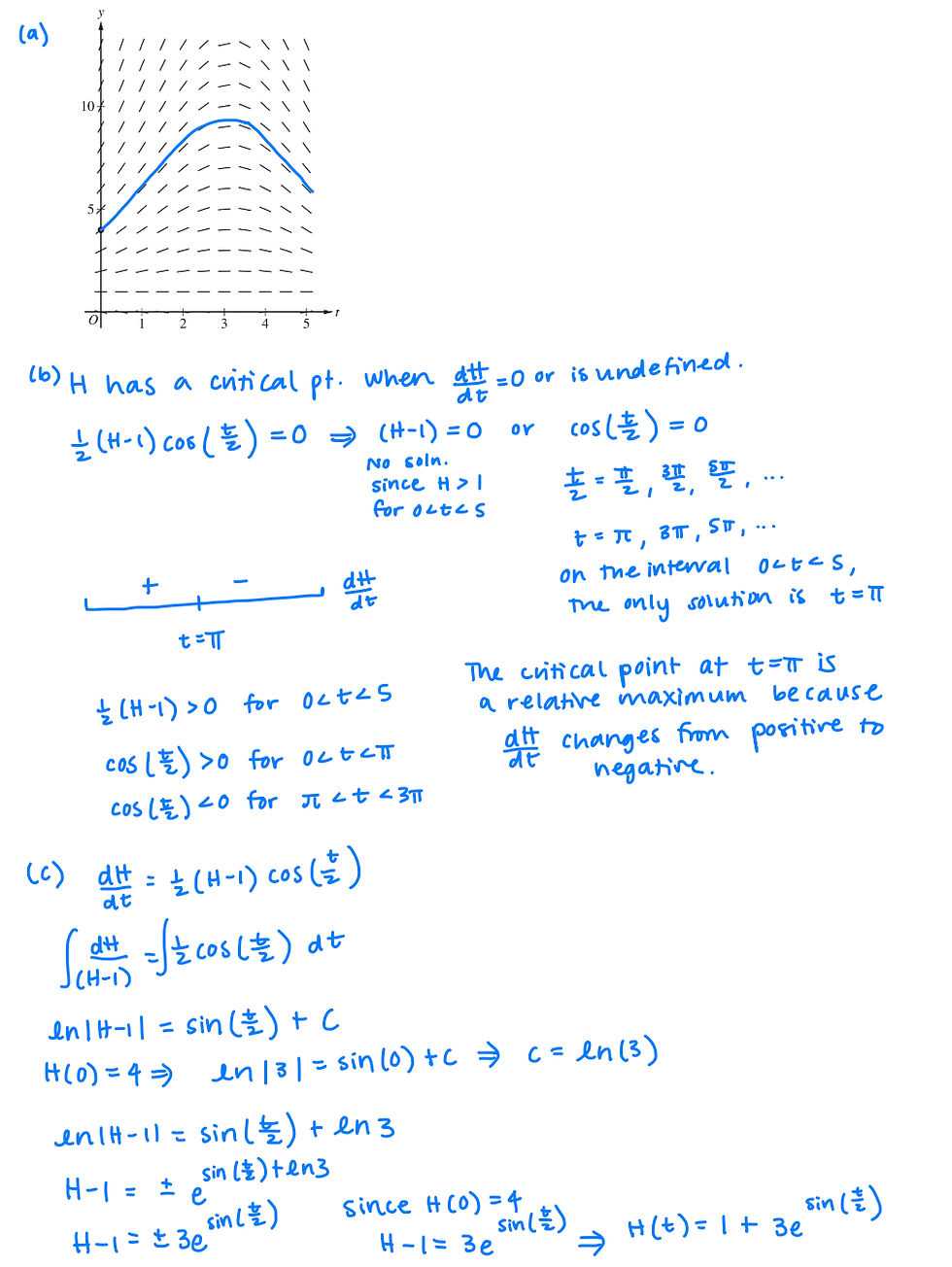
Efficiently managing your time is essential for success, especially when facing time-bound challenges. Proper time management allows you to allocate appropriate time to each task, reduce stress, and ensure that you have enough time to review your work before the deadline. Developing these skills can make a significant difference in your overall performance.

Strategies for Better Time Management

Here are some key strategies to improve how you manage your time during any assessment or practice session:

Set a Time Limit for Each Task: Break your work into manageable sections and assign a specific time frame to each. This helps avoid spending too much time on one question.
Prioritize Questions: Start with the questions you find easiest, as this will build momentum and save time for more challenging tasks later.
Track Your Progress: Regularly check the time and assess your progress. If you’re falling behind, adjust your approach or move on to the next section.

Sample Time Allocation Plan

Creating a time allocation plan helps you structure your approach effectively. Below is a sample plan that can be used to divide your time across different sections:

Section	Time Allotted	Strategy
Easy Questions	10 minutes	Quickly solve and move on
Moderate Difficulty	15 minutes	Carefully read and solve
Challenging Problems	20 minutes	Spend more time, then move on if stuck
Review and Final Check	10 minutes	Go over answers and check for errors

By applying these strategies and sticking to a time allocation plan, you’ll improve your ability to complete tasks efficiently and with greater accuracy.

How to Tackle AP Calculus Word Problems

Word problems often appear as one of the more challenging types of questions in any advanced mathematics test. They require not only a solid understanding of mathematical principles but also the ability to interpret and translate real-world scenarios into mathematical expressions. By following a structured approach, you can break down these problems and solve them effectively.

Steps for Solving Word Problems

When faced with a word problem, it’s essential to follow a logical process that helps you understand the question, identify key information, and find the solution. Here’s how to approach them:

Read the Problem Carefully: Take your time to fully understand the situation. Pay close attention to the given information and what is being asked.
Highlight Key Information: Identify important numbers, terms, and relationships. This will help you focus on the elements that are necessary for solving the problem.
Draw a Diagram or Chart: Visual aids can simplify complex problems by providing a clear representation of the situation. It also helps to map out relationships between different elements.
Translate into Equations: Convert the word problem into a mathematical form. Write down expressions or equations based on the information provided.

Tips for Efficient Problem-Solving

Aside from the basic approach, there are additional strategies that can help you solve word problems more efficiently:

Stay Organized: Keep your work neat and clearly show each step of your thought process. This not only helps avoid errors but also makes it easier to follow your reasoning.
Check Units and Dimensions: Ensure all units of measurement are consistent and that any conversions are done correctly.
Look for Patterns: Some word problems follow predictable patterns. Recognizing these can save you time and effort during the problem-solving process.

By applying these methods and practicing regularly, you’ll improve your ability to solve word problems accurately and efficiently, which is a crucial skill for any mathematical assessment.

Essential Theorems and Formulas to Remember

Mastering certain key principles and equations is critical for success in any advanced mathematics test. These essential theorems and formulas serve as the foundation for solving a wide variety of problems. Keeping them in mind will allow you to approach questions with confidence and precision, minimizing the time spent on complex calculations.

Below is a list of some of the most important theorems and formulas that you should remember:

Theorem/Formula	Description
Fundamental Theorem of Calculus	Relates the derivative of a function to its integral, providing a direct connection between differentiation and integration.
Chain Rule	Used to differentiate composite functions by multiplying the derivative of the outer function by the derivative of the inner function.
Product Rule	Used for differentiating the product of two functions: (uv)’ = u’v + uv’.
Quotient Rule	Used for differentiating the quotient of two functions: (u/v)’ = (vu’ – uv’)/v².
Integration by Parts	A technique for integrating the product of two functions: ∫u dv = uv – ∫v du.
Mean Value Theorem	States that for a continuous function, there is at least one point where the derivative equals the average rate of change over an interval.

These fundamental theorems and formulas are the building blocks for solving more complex problems. By memorizing and understanding their applications, you can tackle a wide range of questions efficiently and effectively.

Effective Strategies for AP Multiple Choice

Multiple-choice questions are designed to test both your understanding and ability to apply various mathematical concepts quickly. While they may appear straightforward, the key to success lies in using effective strategies that help you identify the correct answer while minimizing errors. By developing a systematic approach, you can boost your accuracy and efficiency when tackling these questions.

Approach Each Question Methodically

It’s important to read each question carefully and ensure you fully understand what is being asked before considering the options. Here are some strategies to help guide your thought process:

Read Carefully: Don’t rush through the question. Pay attention to every detail and focus on the specifics to avoid missing subtle hints.
Eliminate Obvious Incorrect Answers: Start by crossing out answers that clearly don’t fit. This reduces the number of options and increases your chances of selecting the correct one.
Estimate Before Calculating: Sometimes, it’s helpful to estimate the answer first. This is especially true for questions involving large numbers or complex operations.

Use Process of Elimination

If you’re uncertain about the correct answer, don’t get stuck. Instead, use the process of elimination to narrow down your options. By ruling out the answers that don’t make sense, you can improve your odds of selecting the right choice. Additionally, if two answers seem similar, there’s a good chance one is close but not quite right. Look for subtle differences to pinpoint the most accurate option.

These techniques, combined with a solid understanding of core mathematical principles, will help you perform confidently on multiple-choice questions. Regular practice with these strategies will lead to better results and increased speed during testing.

Graphing Techniques for Exam Success

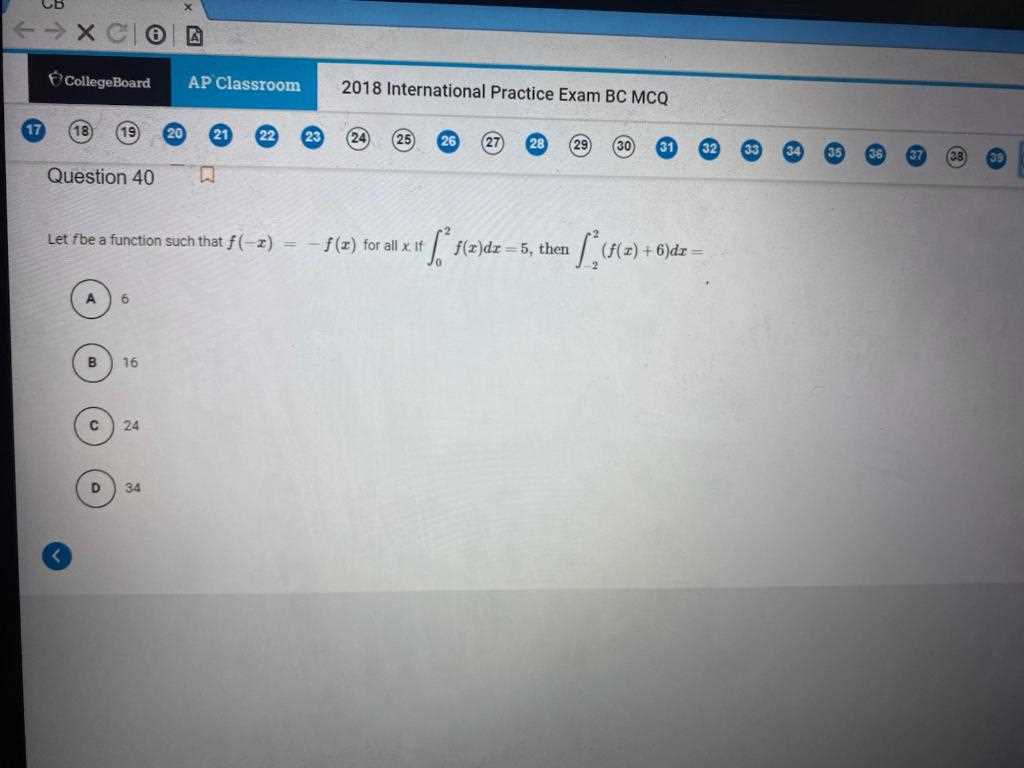
Graphing plays a critical role in many mathematical assessments, allowing you to visualize complex relationships and equations. Mastering graphing techniques can significantly improve your ability to interpret problems and provide clear solutions. Whether working with functions, derivatives, or integrals, a solid understanding of how to graph accurately and efficiently can help you solve problems with greater precision.

Key Graphing Tips to Remember

To make the most of your graphing skills, focus on the following strategies:

Identify Key Features: Before plotting, identify important points such as intercepts, maxima, minima, and asymptotes. These key features provide valuable insights into the overall behavior of the graph.
Understand the Function’s Behavior: Know how the graph of the function should behave based on its type. For example, polynomial functions typically have smooth curves, while rational functions may exhibit vertical or horizontal asymptotes.
Label Your Axes: Ensure that both axes are clearly labeled with appropriate scales. This makes your graph easier to understand and interpret.

Graphing Strategies for Efficiency

When under time pressure, efficiency is key. Here are some strategies to help you graph quickly without sacrificing accuracy:

Sketch First: If exact plotting isn’t possible, start by sketching a rough graph. This can help you visualize the function’s behavior and guide your thinking before refining the graph.
Use Symmetry: Many functions exhibit symmetry, which can save time. For example, even functions have symmetry about the y-axis, while odd functions are symmetric about the origin.
Focus on Critical Points: Don’t worry about plotting every single point. Focus on key points that provide a clear understanding of the graph’s shape.

By mastering these graphing techniques and integrating them into your problem-solving approach, you will be better prepared to tackle graph-based questions with confidence and accuracy during the test.

Test Tips for Better Scores

Improving your score on any mathematical assessment requires a combination of preparation, strategy, and careful execution. While practice is essential, it’s equally important to adopt effective techniques during the test itself. By focusing on key strategies, you can maximize your performance and increase your chances of achieving the best possible result.

Preparation is Key

The foundation for success begins long before the test day. Proper preparation helps to build confidence and ensure you’re familiar with all relevant concepts:

Review Core Concepts: Make sure you understand fundamental topics and methods, such as function analysis, rate of change, and integration techniques. A strong grasp of the basics will help you tackle a variety of questions effectively.
Practice Regularly: Consistent practice with a variety of problems helps reinforce learning and identify areas where you need improvement. Working through problems of different difficulty levels will enhance your problem-solving skills.
Understand the Format: Familiarize yourself with the test format and question types. Knowing what to expect helps reduce anxiety and allows you to allocate time efficiently.

Strategies for Test Day

On the day of the test, a strategic approach will help you use your time effectively and avoid common pitfalls:

Read Questions Carefully: Take your time to understand what each question is asking before jumping into the solution. Sometimes the wording can be tricky, and careful reading can prevent errors.
Manage Your Time: Be mindful of time limits. Allocate specific amounts of time to each section, and don’t spend too much time on a single question. Move on if you’re stuck and return to it later if necessary.
Check Your Work: If time permits, always review your answers. Double-check your calculations and make sure you’ve answered each question fully.

By combining thorough preparation with strategic thinking during the test, you can approach your assessment with confidence and achieve the highest possible score.

How to Use a Calculator During the Exam

Using a calculator effectively can significantly boost your performance during a timed mathematical assessment. However, it’s important to use it strategically, ensuring it complements your problem-solving skills rather than relying on it too heavily. The right approach will allow you to save time, avoid mistakes, and enhance your overall efficiency on the test.

Familiarize Yourself with the Calculator

Before you sit for the assessment, take time to become familiar with the specific calculator allowed for the test. Knowing the functions and capabilities of the calculator will allow you to use it more effectively:

Understand All Functions: Review the different features of the calculator, such as graphing capabilities, memory functions, and built-in formulas. This knowledge will help you select the best tool for each problem.
Practice with the Calculator: Before the test, practice solving problems using the calculator. This ensures you are comfortable with entering equations, storing values, and using advanced features.
Master Shortcuts: Learn the most efficient ways to input equations and solve problems quickly. Knowing calculator shortcuts can save precious time during the exam.

When to Use the Calculator

While a calculator can be a helpful tool, it’s essential to know when and how to use it properly during the test:

Use for Complex Calculations: For lengthy or complicated calculations, use the calculator to ensure accuracy. This is especially helpful for computations that would be time-consuming or prone to error if done manually.
Graphing Functions: If the test allows for graphing, use your calculator to plot graphs of functions. This can help you visualize problems and identify solutions more easily.
Avoid Overreliance: While the calculator can speed up certain tasks, don’t rely on it for every step. Always understand the underlying concepts and use the calculator as a tool, not a crutch.

By mastering the use of your calculator before the test and strategically applying it during the assessment, you can maximize its potential and optimize your performance.

Understanding Limits and Derivatives Better

Grasping the core concepts of rates of change and behavior of functions at specific points is essential for excelling in mathematical assessments. By improving your understanding of limits and derivatives, you’ll be better prepared to analyze and solve problems that involve instantaneous changes or the behavior of functions as they approach certain values. These concepts are fundamental in many areas of mathematics and are crucial for a deep understanding of various real-world applications.

Limits play a key role in understanding the behavior of functions as they approach a certain value. Whether you’re evaluating a function as it approaches a specific number or infinity, the concept of limits allows you to describe how the function behaves at those points. This understanding forms the basis for defining continuity and differentiability of functions.

Derivatives, on the other hand, deal with the rate at which a function is changing at any given point. They provide critical information about the steepness of a curve and can be used to solve problems involving motion, growth rates, and optimization. Being able to differentiate various types of functions efficiently is a vital skill for tackling complex problems.

To improve your understanding of these concepts, here are a few key strategies:

Practice with Real-World Examples: To grasp the abstract nature of these concepts, apply them to practical examples. For instance, consider how the speed of a car (rate of change) can be represented as a derivative and how the distance traveled can be analyzed using limits.
Work Through Different Types of Problems: Limits and derivatives can appear in various forms, from simple polynomial functions to more complex rational and trigonometric expressions. Working through diverse problems will help you understand when and how to apply specific techniques.
Understand the Rules and Theorems: Master key rules like the chain rule, product rule, and L’Hopital’s rule for limits. Understanding these theorems will make it easier to solve problems efficiently and correctly.

By reinforcing your knowledge of limits and derivatives through regular practice and real-world applications, you will not only improve your problem-solving skills but also develop a stronger conceptual foundation for more advanced mathematical topics.

Preparing for the Free Response

In order to succeed in the free response section of a mathematical assessment, it’s essential to understand not only the required techniques but also the structure of the problems. These types of questions often test your ability to apply various concepts in a clear, logical sequence. Preparation for this section involves mastering problem-solving strategies, as well as being able to communicate your reasoning in a well-organized manner.

Understanding the Problem is the first step. Carefully read each question to identify what is being asked. Many problems involve multiple parts, each requiring different approaches or calculations. Break down the question into manageable steps, and make sure you understand the underlying concepts before proceeding.

Showing Work Clearly is critical. Unlike multiple-choice questions, free-response problems assess your ability to demonstrate thought processes and mathematical reasoning. Use proper notation, label your work, and explain each step of your solution. Even if the final answer is correct, incomplete or unclear work can lead to lost points.

Managing Your Time effectively is another key to success. Allocate time to each question based on its complexity and point value. Don’t get stuck on a single problem for too long–move on and come back to it later if necessary. Having a strategy for time management can help ensure that you address every question within the allotted timeframe.

Practice Under Real Conditions is one of the best ways to prepare. Simulate test conditions by setting aside time for untimed problem-solving and timed practice runs. This approach will help you become familiar with the format and reduce any test anxiety you might have.

By focusing on clear communication, strategic time management, and consistent practice, you’ll be better equipped to handle the challenges presented in the free-response section of the assessment. Remember, it’s not just about finding the right answer–it’s about demonstrating your understanding of the concepts in a structured and effective way.

Building Confidence Before the Test

Approaching a major assessment with confidence can significantly improve your performance. Preparation is key, but equally important is maintaining a positive mindset. By focusing on strategies to build your self-assurance, you can reduce stress and perform at your best on test day. This section outlines several effective techniques to help you feel more confident as the test approaches.

Mastering the Material

Thoroughly understanding the content is the first step in building confidence. Review all key concepts and problem types, and make sure you are comfortable with the methods and techniques needed to solve them. Consistent study and focused practice are essential for reinforcing your knowledge. As you work through problems, pay attention to your progress and note areas where you feel confident versus areas that may need more attention.

Simulating Test Conditions

Taking timed practice sessions can be a game-changer. By simulating the actual testing conditions, you familiarize yourself with the format and the pressure of time. This practice helps you manage your time effectively during the actual assessment, allowing you to approach each section without feeling rushed or overwhelmed. Try to replicate the test environment as closely as possible–no distractions, no interruptions, and a strict time limit.

Positive Self-Talk and Stress Management

Maintain a positive mindset by focusing on your strengths and past successes. Positive self-talk can reduce feelings of anxiety and replace self-doubt with determination. Along with this, it’s important to incorporate stress management techniques, such as deep breathing, meditation, or physical exercise. These practices can help calm your nerves and ensure that you’re mentally prepared to tackle the test with clarity and focus.

By reinforcing your knowledge, simulating the test conditions, and managing stress effectively, you can approach the assessment with confidence and a sense of readiness. Trust in your preparation, stay focused, and remember that every challenge is an opportunity to demonstrate what you know.