Lesson 10.6 Practice A Answers Explained

This section offers a comprehensive breakdown of essential exercises designed to help you reinforce your understanding of the material. The focus is on developing critical problem-solving skills while ensuring a deeper grasp of the underlying principles. By reviewing each step, you’ll improve your ability to tackle complex tasks with confidence.

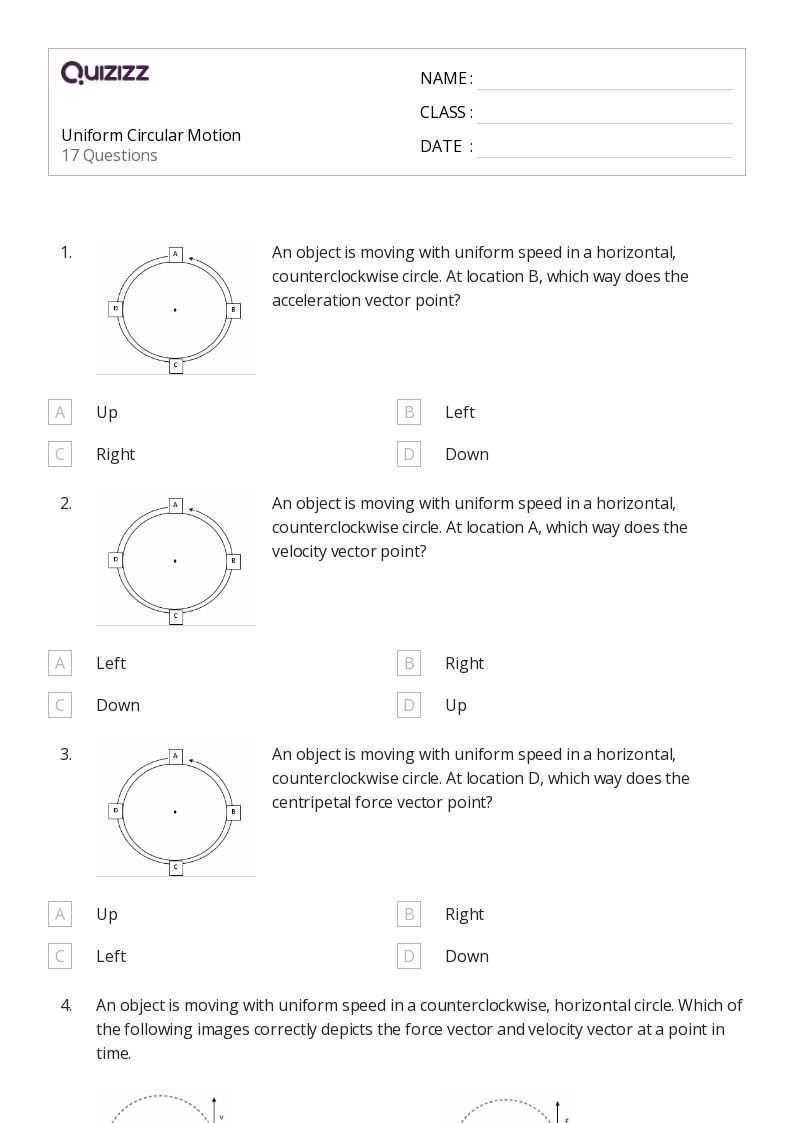
Step-by-step guidance is provided to ensure clarity in every approach. The goal is to enhance your ability to analyze and apply various strategies effectively. Each solution is explained in detail, helping you understand the logic behind every decision.

As you explore these exercises, you’ll gain valuable insights into the most effective methods for overcoming challenges and refining your overall proficiency. Whether you’re revisiting familiar concepts or encountering new ones, this section is designed to support your learning journey and boost your confidence in tackling related topics.

Lesson 10.6 Practice A Answers Overview

This section provides an overview of the key solutions and strategies for the exercises designed to test your grasp of the core material. It focuses on guiding you through each problem, ensuring that you not only arrive at the correct outcomes but also understand the reasoning behind each step. The goal is to help you develop a deeper comprehension and enhance your problem-solving skills.

Each solution is carefully broken down to highlight the methods used in reaching the final result. By understanding the underlying processes, you will be able to apply these techniques to similar problems in the future. The aim is to make you comfortable with both the approach and the reasoning, fostering a more intuitive understanding of the concepts.

Understanding Key Concepts in Lesson 10.6

To effectively tackle the exercises, it’s important to first understand the foundational principles that guide the problems. The material builds on various core ideas, each of which plays a crucial role in how you approach the tasks. Mastery of these concepts is essential for progressing through more complex scenarios with confidence and accuracy.

Core Ideas for Success

The key to solving these exercises lies in understanding the fundamental techniques that underpin each question. These methods are not only essential for the specific problems at hand but also form the basis for applying similar strategies in future challenges. By focusing on these techniques, you’ll develop a stronger intuition for the material.

Building Problem-Solving Skills

Another critical aspect of mastering this content is improving your problem-solving abilities. By consistently practicing and reviewing different approaches, you will refine your skillset. Emphasis on logical reasoning and step-by-step breakdowns will help you approach each task with greater clarity and precision.

Common Mistakes in Practice A

While working through these exercises, there are several frequent errors that can hinder progress. Recognizing and addressing these common mistakes is key to improving your understanding and avoiding setbacks. Being aware of typical missteps will help you refine your approach and boost your accuracy in future tasks.

Frequent Errors to Watch Out For

Misunderstanding the Problem Statement: It’s easy to misinterpret the question, which can lead to incorrect solutions. Always read the instructions carefully to ensure you understand what is being asked.
Skipping Key Steps: Rushing through problems can cause you to overlook important intermediate steps. Taking the time to go through each part methodically is crucial.
Incorrect Application of Formulas: Using the wrong formula or applying it incorrectly is another common mistake. Ensure you’re using the correct method for each situation.
Overlooking Units: Not paying attention to units or dimensions can lead to mismatches in calculations. Always double-check units before finalizing your answers.
Not Double-Checking Work: Failing to review your answers before submission can result in avoidable errors. A final check often reveals overlooked mistakes.

How to Avoid These Mistakes

Read carefully: Make sure you fully understand the task before starting. Clarify any doubts before moving on.
Break down the process: Work through problems step by step, checking each part before moving forward.
Check your formulas: Always verify that the formula you’re using is correct and applies to the situation.
Be meticulous with units: Ensure that all units are consistent and correctly accounted for throughout the problem.
Review your answers: Never skip the review process–double-check all work for accuracy.

How to Approach Practice A Questions

When tackling the exercises, it’s essential to approach each one with a clear strategy. The right mindset and structured process can make a significant difference in your ability to solve problems effectively. By following a step-by-step approach, you can ensure that you understand the concepts and apply the correct methods to reach the solution.

Steps for Effective Problem Solving

Read the Problem Carefully: Begin by fully understanding the task. Pay attention to all details, including any specific instructions or constraints.
Identify Key Information: Extract the most important data from the question. Focus on numbers, variables, and any relationships mentioned.
Choose the Right Method: Select the appropriate approach or formula based on the problem’s requirements. If you’re unsure, try to recall similar problems you’ve worked through before.
Break Down the Problem: Divide the task into smaller, manageable steps. Solving in stages will make the process less overwhelming.
Double-Check Your Work: Once you have a solution, review your steps to ensure everything is correct. This will help catch any errors or missed information.

Tips for Improved Efficiency

Stay Organized: Write down each step clearly, especially when dealing with complex calculations or multiple stages.
Manage Your Time: Don’t spend too long on any one question. Move on if you’re stuck and return to challenging problems later.
Practice Consistently: The more you practice, the more comfortable you’ll become with identifying patterns and applying solutions.
Ask for Help: If you’re unsure about a method or approach, seek clarification from a tutor, peer, or online resources.

Breaking Down Problems

When approaching a problem, it’s essential to break it into smaller, more manageable components. This method allows you to focus on each element individually, ensuring a thorough understanding and more accurate results. By analyzing each step carefully, you can identify patterns and apply the correct strategies to reach the solution efficiently.

Step	Description	Common Mistakes
Step 1: Understand the Problem	Read the problem carefully, identify the key information and requirements.	Rushing through the question, missing crucial details.
Step 2: Identify the Method	Determine the best approach to solve the problem, including any formulas or strategies.	Using the wrong formula or technique.
Step 3: Break the Problem into Parts	Divide the problem into smaller, manageable steps to make it less overwhelming.	Trying to solve everything at once without a clear plan.
Step 4: Solve Step by Step	Work through each part logically, checking progress after each step.	Skipping intermediate steps or jumping ahead.
Step 5: Verify Your Solution	Double-check calculations and verify that your final answer makes sense.	Not reviewing the work, leading to simple errors.

By following these steps, you can approach any problem systematically, ensuring that you tackle each aspect of the task with precision. This structured approach not only helps you solve the current problem but also strengthens your overall problem-solving abilities for future challenges.

Step-by-Step Guide to Answers

To solve the exercises effectively, it’s important to follow a clear and structured approach. By breaking down each problem into smaller tasks, you can address the most complex components one at a time. This method ensures you don’t miss any details and gives you a more thorough understanding of the material as you work through each step.

Step	Action	Explanation
Step 1: Analyze the Question	Read the problem carefully and identify all the important details.	Understanding the question is crucial before attempting to solve it. Make sure you know exactly what is being asked.
Step 2: Identify Relevant Information	Extract key data such as numbers, variables, and relationships.	Pinpoint the information that will help you solve the problem. Leave out irrelevant details to avoid confusion.
Step 3: Choose the Right Approach	Determine which method or formula applies best to the problem.	Select the correct strategy based on the problem’s requirements, whether it involves equations, graphs, or logical reasoning.
Step 4: Perform Calculations	Carry out the necessary steps to solve the problem.	Follow the chosen method step by step, ensuring accuracy in every calculation. Write down all intermediate steps to stay organized.
Step 5: Verify the Solution	Double-check your solution to confirm that it answers the question correctly.	Review all steps and calculations to ensure that your solution is accurate and complete. If possible, recheck using a different method.

By following this step-by-step approach, you can ensure that each problem is tackled systematically and that you arrive at the correct solutions. Taking the time to break down the problem will not only increase your efficiency but also your confidence in solving similar tasks in the future.

Tips for Mastering Practice A

To excel in solving problems effectively, it’s important to adopt a focused approach that helps you grasp key concepts while also refining your problem-solving techniques. Success comes not just from working through tasks but from building a deeper understanding of the material and approaching each exercise strategically. By following a few practical tips, you can enhance both your efficiency and accuracy in tackling challenging problems.

Focus on Key Concepts: Ensure you have a solid grasp of the fundamental ideas before attempting to solve the problems. A strong understanding of the core concepts makes it easier to apply the correct methods.
Take Your Time: Don’t rush through tasks. Approach each problem thoughtfully, breaking it down into smaller, manageable steps to avoid errors and oversights.
Practice Regularly: The more you practice, the more familiar you’ll become with common techniques and problem types. Consistency leads to better retention and mastery.
Analyze Mistakes: Reviewing your errors is one of the best ways to improve. Identify where you went wrong, learn from it, and make sure not to repeat the same mistakes.
Stay Organized: Write down intermediate steps clearly and keep your work neat. This will help you track your progress and catch potential mistakes early.
Seek Clarification: If you find yourself stuck, don’t hesitate to ask for help. Consulting a peer, tutor, or online resource can provide valuable insights and prevent unnecessary frustration.

By implementing these strategies, you can ensure that you approach each task with confidence and skill. Mastery comes with consistent effort and a mindful approach, so keep practicing, stay organized, and reflect on your progress to continue improving.

Review of Answering Techniques

Mastering the art of answering questions involves more than just providing a response; it requires a thoughtful and systematic approach to ensure clarity and correctness. By refining your techniques, you can enhance the quality of your solutions and improve your overall performance. Understanding the essential steps involved in crafting a well-structured answer is key to achieving success in problem-solving tasks.

Key Strategies for Effective Responses

Understand the Question: Before starting, take the time to carefully read and understand what is being asked. Make sure you identify the key components and focus areas.
Organize Your Thoughts: Break down the problem into smaller, more manageable parts. This will help you approach the question methodically and avoid missing any critical details.
Use Clear and Concise Language: Express your answers clearly. Avoid unnecessary jargon and stay focused on the core points to ensure your explanation is easy to follow.
Check Your Work: Always review your answers before finalizing them. Look for possible mistakes, misinterpretations, or missed steps to make sure your solution is accurate.

Common Pitfalls to Avoid

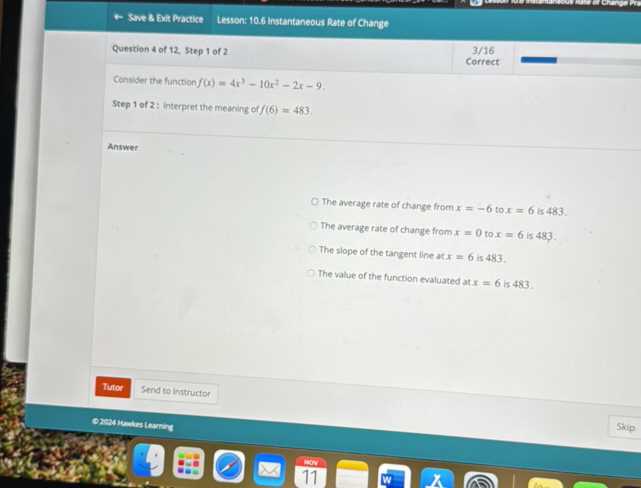
Rushing Through the Response: Trying to finish too quickly often leads to careless mistakes. Take your time to think through each step carefully.
Ignoring Units or Details: Small details like units of measurement or specific instructions are crucial. Failing to include them can lead to incomplete or incorrect answers.
Skipping Intermediate Steps: Don’t skip steps in your solution. Writing down intermediate steps can help you identify errors early and strengthen your explanation.

By implementing these techniques, you can significantly improve the quality and accuracy of your responses. The key to mastering problem-solving lies in consistent practice and attention to detail, so take the time to refine your approach with each new task.

Commonly Asked Questions About Lesson 10.6

When tackling complex exercises or concepts, it’s natural to have questions. Many learners encounter similar challenges when trying to understand the material, which is why reviewing common queries can provide clarity. Addressing frequently asked questions helps demystify the process and allows students to approach the tasks with greater confidence.

What is the best way to prepare for the tasks? The key to success lies in understanding the fundamental principles before attempting the exercises. Make sure you are comfortable with the core concepts and review any relevant examples to familiarize yourself with the structure.
How do I know if my solution is correct? After completing each problem, always double-check your work. Ensure that each step logically follows from the previous one, and if possible, use alternative methods or verification techniques to confirm your results.
What should I do if I get stuck on a particular problem? If you’re struggling with a specific part of the task, break it down into smaller, more manageable components. Look for patterns or revisit similar problems to identify the correct approach. If needed, consult additional resources or ask for clarification.
How important is the order in which I solve the problems? While the order can vary depending on the task, it’s generally a good idea to start with the simpler problems first. This helps build confidence and gives you a foundation to tackle more complex questions later.
How can I improve my speed while maintaining accuracy? Regular practice is the key to improving both speed and precision. As you work through more problems, you’ll become more familiar with the methods and develop a quicker response time without sacrificing the quality of your solutions.

By addressing these common concerns, you can reduce any anxiety and approach the challenges with a clearer understanding. Remember, persistence and practice are crucial in mastering any material, so stay focused and keep refining your techniques.

Improving Your Problem-Solving Skills

Enhancing your problem-solving abilities requires a combination of strategic thinking, consistent practice, and an understanding of core techniques. With the right approach, you can refine your ability to tackle even the most challenging questions. Building this skill set involves not just memorizing formulas or methods, but learning how to apply them effectively in various contexts. This section will explore practical ways to sharpen your problem-solving proficiency and boost your confidence in solving complex tasks.

Key Strategies for Better Problem-Solving

Understand the Problem Thoroughly: Before diving into solving, take the time to understand every aspect of the problem. Read through the instructions carefully and identify the goal.
Break It Down into Steps: Divide complex problems into smaller, manageable parts. This makes the overall solution easier to approach and helps you stay focused on each individual component.
Consider Multiple Approaches: Don’t settle on the first method that comes to mind. Explore different strategies and choose the one that makes the most sense given the circumstances.
Analyze and Learn from Mistakes: When things don’t go as planned, take time to review your errors. This analysis helps you learn from your mistakes and avoid repeating them in the future.

Practical Tips for Continuous Improvement

Tip	Benefit
Regular Practice	Improves familiarity with common techniques and increases speed and accuracy.
Work in a Timed Environment	Helps build efficiency under pressure, simulating real-world conditions.
Seek Feedback	Offers valuable insights that can help refine your approach and reduce errors.

By consistently applying these strategies, you can improve your problem-solving abilities and become more adept at tackling a wide variety of challenges. Remember, progress comes with practice, and refining these skills will enable you to approach tasks with greater ease and precision.

Detailed Explanations of Practice A Solutions

Understanding the reasoning behind each solution is a crucial aspect of mastering any problem. It’s not enough to simply arrive at the correct answer; grasping the steps and logic involved ensures you can apply the method to other situations. In this section, we will provide clear and comprehensive explanations of how to approach and solve the exercises step-by-step, breaking down the reasoning and calculations for each problem.

Step 1: Identify Key Information – Begin by extracting the relevant details from the problem statement. This includes numbers, variables, and specific conditions that will guide your solution process.
Step 2: Choose the Appropriate Method – Based on the problem type, select the best technique or formula to use. If there are multiple approaches, evaluate each one to determine the most efficient path.
Step 3: Execute the Calculations – Carefully perform the necessary operations. Double-check each step to avoid simple errors, especially when working with complex numbers or functions.
Step 4: Verify the Solution – Once you’ve arrived at a potential answer, verify it by plugging the result back into the problem or checking it against alternative methods. This confirms the solution’s accuracy.

Each of these steps plays a crucial role in solving the exercises correctly. By understanding how to systematically break down a problem and apply the correct methodology, you can approach any challenge with confidence and clarity.

Example Problem Breakdown

Problem: Solve for x in the equation 2x + 5 = 15
Step 1: Isolate the variable x – Subtract 5 from both sides: 2x = 10.
Step 2: Solve for x – Divide both sides by 2: x = 5.
Verification – Substitute x = 5 into the original equation: 2(5) + 5 = 15, confirming the solution is correct.

By following this methodical approach to problem-solving, you can ensure a deeper understanding of each solution and become more proficient in tackling similar questions in the future.

How Practice A Relates to Lesson 10.6

The exercises in this section are designed to reinforce and apply the key concepts introduced earlier. Each problem builds on foundational knowledge and challenges you to apply the skills learned to solve more complex situations. By connecting theory with practical application, this set of problems helps to solidify understanding and enhance your ability to approach similar tasks in the future.

The connection between these exercises and the previous material is essential for mastery. Here’s how these problems align with the lessons covered:

Reinforcement of Key Concepts: The tasks encourage you to revisit and apply the main ideas discussed earlier, ensuring that you grasp the core principles thoroughly.
Development of Problem-Solving Skills: As you work through these exercises, you enhance your ability to break down problems, identify necessary steps, and implement solutions efficiently.
Practice with Real-World Applications: Many of the exercises simulate real-life situations where the concepts you’ve learned can be applied, helping to bridge the gap between theory and practice.

In essence, these tasks not only test your understanding but also push you to refine your skills by working through progressively challenging scenarios. By doing so, they contribute to a deeper comprehension of the subject matter and prepare you for more advanced topics down the line.

Building on What You’ve Learned

Review the Concepts: Start by revisiting the main concepts from the previous sections before tackling these exercises.
Apply What You Know: Use the techniques you’ve already learned to approach each problem methodically, adapting them to the specific context of each task.
Check Your Work: Once you’ve solved the problem, verify your solution to ensure accuracy and reinforce your learning.

By actively engaging with these exercises, you will strengthen your grasp of the subject and develop the confidence needed to tackle even more complex challenges in the future.

Strategies for Tackling Difficult Questions

When faced with challenging problems, it’s important to approach them systematically rather than becoming overwhelmed. A structured approach can help break down the complexity and lead you toward a solution. By applying proven techniques, you can approach even the toughest questions with confidence and clarity.

Here are some strategies to consider when dealing with difficult problems:

Read the Problem Carefully: Take your time to thoroughly understand the question. Identify the key components and what exactly is being asked. Skimming or rushing can lead to missing important details.
Break it Down: Divide the problem into smaller, more manageable parts. Address each segment one at a time, which will make the entire task less intimidating.
Look for Patterns: Many problems follow certain patterns or structures. Recognizing these patterns can simplify the problem and suggest a method for solving it more efficiently.
Use a Step-by-Step Approach: Don’t attempt to jump to the solution. Methodically work through the problem, step by step, ensuring that you are building on each previous stage.
Eliminate Distractions: Focus your attention solely on the problem at hand. Minimize external distractions so that you can think more clearly and critically about the task.
Don’t Be Afraid to Make Mistakes: Trial and error is often part of the process. Making mistakes can help identify gaps in understanding and lead to better insights.

By implementing these strategies, you can improve your problem-solving skills and navigate even the most complex questions with a clearer, more organized mindset. With practice, you’ll become more adept at recognizing and applying these techniques, ultimately boosting your confidence and performance.

Key Takeaways from Practice A Answers

Reflecting on completed exercises can provide invaluable insights and help consolidate knowledge. By reviewing solutions carefully, learners can identify common strategies and improve their approach to problem-solving. These takeaways not only highlight the key concepts but also reveal how to approach similar challenges in the future with greater efficiency and confidence.

Understanding Core Concepts

One of the most important lessons learned is the deeper understanding of core principles. By breaking down each problem and examining the solution process, it becomes easier to recognize patterns and establish connections between different concepts. This helps build a solid foundation for tackling more complex topics in the future.

Enhancing Problem-Solving Skills

Another key takeaway is the enhancement of problem-solving techniques. By analyzing different approaches to the same problem, learners can develop a toolkit of strategies, such as step-by-step methods, logical reasoning, and pattern recognition. These techniques not only improve efficiency but also foster creativity in approaching various types of challenges.

Ultimately, these exercises provide critical practice that strengthens both theoretical knowledge and practical application. As a result, learners become more proficient in their ability to tackle similar questions and apply these skills in diverse contexts.

Resources for Further Learning

Continuing your education and deepening your understanding of the material can be achieved through various resources. These tools offer additional perspectives, practice, and insights to reinforce the concepts learned. Whether you are looking to strengthen your knowledge in specific areas or expand into new topics, there are a multitude of ways to keep progressing.

Online Courses and Tutorials

Many websites offer comprehensive courses that dive deeper into related topics. Platforms like Coursera, edX, and Udemy provide structured learning paths with video lectures, quizzes, and assignments. These courses often feature expert instructors who can offer additional explanations and clarifications.

Interactive Platforms

Interactive learning platforms such as Khan Academy and Codecademy allow students to practice directly on the platform. They offer a hands-on approach to mastering new concepts with instant feedback, helping you track progress and refine your skills effectively.

Books and eBooks

Books remain a reliable and detailed source for expanding knowledge. Many textbooks and guides provide step-by-step explanations, real-world applications, and exercises that help solidify your understanding. Look for textbooks from reputable authors or publishers to get in-depth insights into the subject.

Discussion Forums and Study Groups

Engage with other learners through online discussion forums such as Stack Exchange or Reddit, where you can ask questions, share insights, and find solutions to common problems. Joining study groups or attending live study sessions can also be beneficial for collaborative learning and gaining new perspectives.

By utilizing these resources, you can continue refining your skills, explore more complex concepts, and ensure a thorough mastery of the material.

Preparing for the Next Lesson

As you complete each stage of your learning, it’s essential to prepare for upcoming topics to ensure continued success. Building a solid foundation for what’s next helps you engage more effectively with new material and reinforces what you’ve already learned. Taking the time to review, plan, and set goals will make the transition to more advanced concepts smoother and more manageable.

Reviewing Key Concepts

Before moving forward, take a moment to reflect on the key ideas you’ve encountered. Reviewing your notes, revisiting exercises, and going over any challenging areas will strengthen your understanding. Pay attention to areas where you might have struggled to ensure you are fully prepared for future topics that may build on these foundations.

Setting Learning Goals

One way to stay on track is by setting specific, measurable goals for the upcoming lessons. Identify areas you’d like to explore in more depth or skills you aim to refine. Having a clear direction will help you maintain focus and stay motivated as you progress through the curriculum.

Additionally, make sure to gather any materials or resources that might be useful for the upcoming lessons. This could include reference books, online articles, or additional practice exercises. Being prepared will enable you to make the most of each lesson and tackle more advanced topics with confidence.