Lesson 2.3 Practice A Geometry Answers Guide

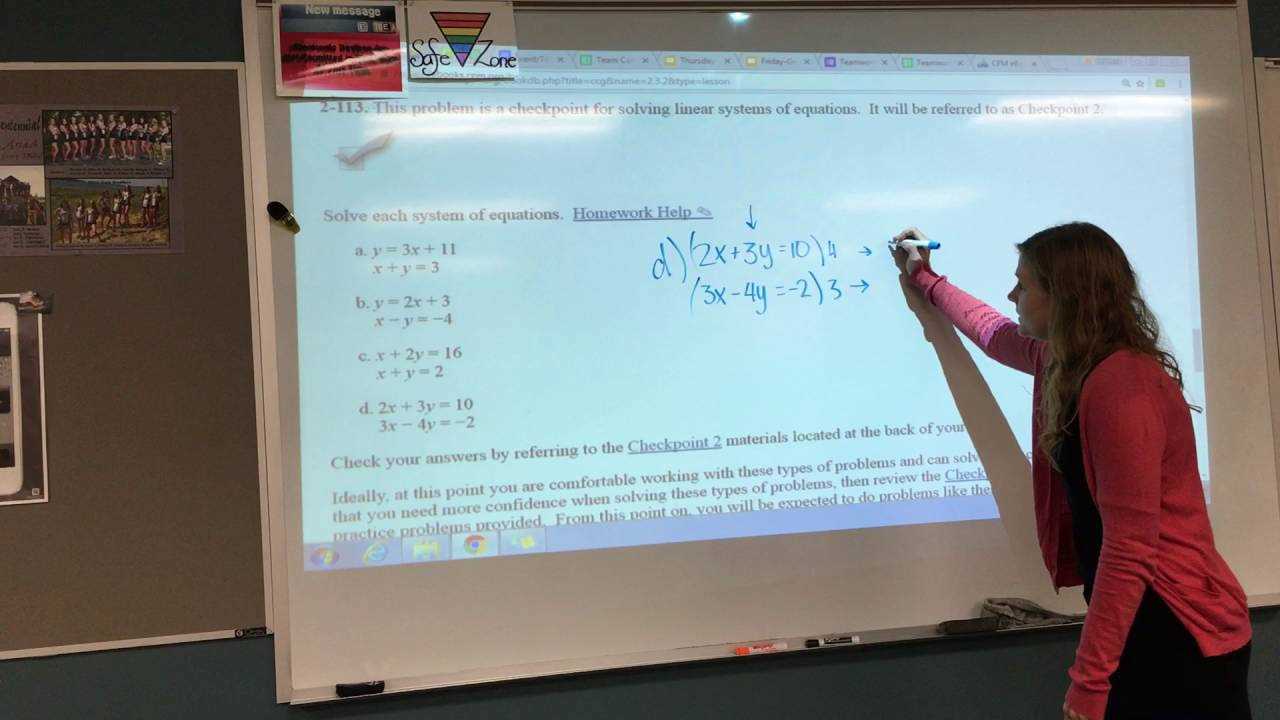
In this section, we will explore essential principles that form the foundation of advanced problem-solving techniques. The focus is on strengthening your ability to apply logical reasoning to complex tasks, ensuring that you can tackle various challenges effectively.

By the end of this guide, you will have a deeper understanding of how to break down mathematical problems, apply core formulas, and evaluate your results. This process will not only sharpen your skills but also boost your confidence in approaching similar topics in the future.

Critical thinking and careful analysis are at the heart of these exercises. As you work through them, you’ll develop a more intuitive grasp of the subject, allowing you to make connections and recognize patterns with ease.

Understanding Key Mathematical Solutions

This section delves into the process of interpreting and solving mathematical exercises that require logical reasoning and precision. The goal is to gain a clear understanding of each step involved in deriving the correct solutions. By breaking down the steps, you will be able to better comprehend the underlying concepts and approaches.

As you work through these examples, focus on how to identify the most effective strategies for solving each problem. Each task presents unique challenges that help refine your skills and enhance your ability to recognize patterns, apply formulas, and verify results accurately.

Familiarity with common techniques will help you approach similar problems with greater ease and confidence. Developing a methodical approach to these exercises not only improves your technical knowledge but also prepares you for more advanced topics in the subject.

Key Concepts in Advanced Mathematical Exercises

This section introduces the foundational principles and critical ideas that underpin the most common types of problems you will encounter. Understanding these core concepts is essential for solving complex tasks effectively. The focus is on recognizing patterns, applying relevant formulas, and mastering the techniques necessary for precise calculations and logical deductions.

Essential Techniques for Problem Solving

Effective problem-solving relies heavily on recognizing which techniques are best suited for each specific situation. Whether it’s identifying geometric relationships, applying algebraic operations, or using measurement tools, knowing the right approach allows for more efficient and accurate solutions.

Formulas and Theorems You Must Know

Several key formulas and theorems serve as the backbone for many exercises in this topic. Understanding their applications and the relationships between different concepts will empower you to solve problems with ease. Familiarity with these principles helps ensure that you can approach each problem from the most efficient angle.

How to Approach Mathematical Problems

When facing complex problems, having a structured approach is essential for finding solutions efficiently. The first step is to thoroughly analyze the task, identify what is being asked, and determine which methods or tools are most appropriate. By breaking down the problem into smaller parts, you can ensure each element is addressed properly, leading to a more accurate result.

Identifying Key Information

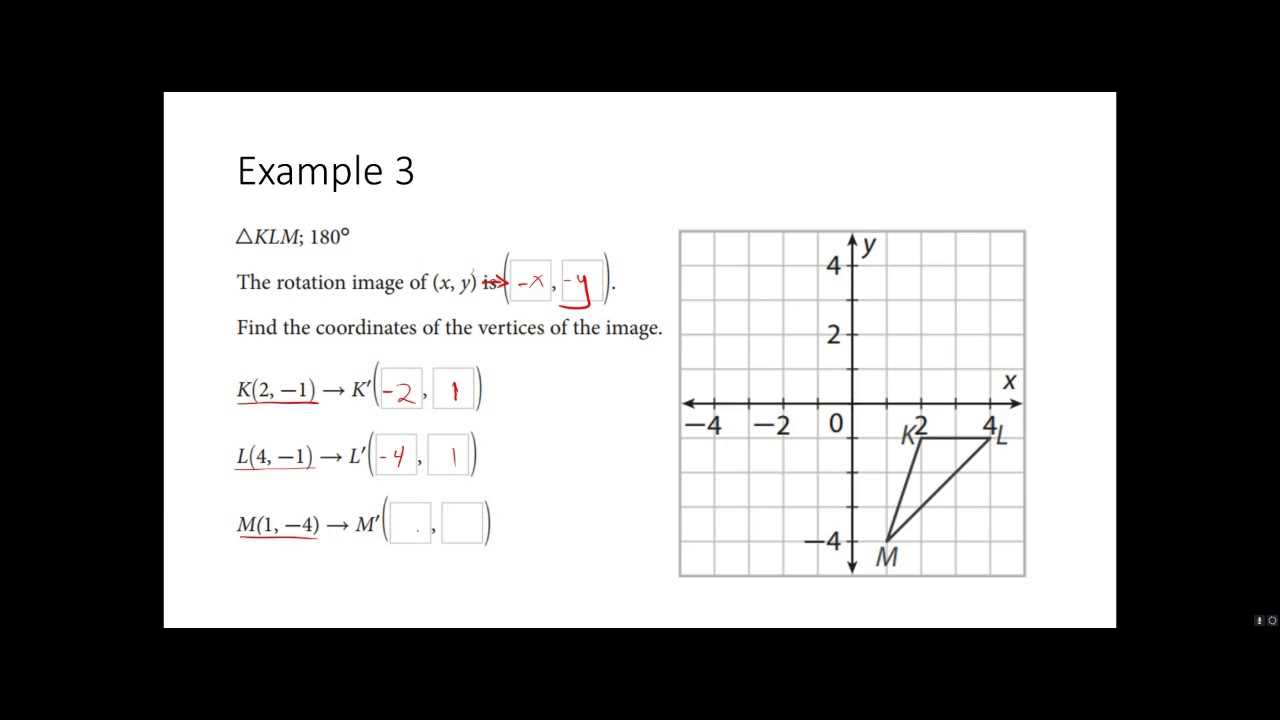
Start by highlighting the critical elements of the problem. Look for given data, such as measurements, relationships between shapes, and any constraints that are provided. Understanding these aspects will guide you in selecting the right method to proceed. Focusing on essential details helps eliminate unnecessary distractions and improves your focus.

Choosing the Right Strategy

Once you have a clear grasp of the problem, choose a strategy that aligns with the type of task you’re tackling. Whether it’s applying a theorem, performing calculations, or visualizing the situation through diagrams, using the correct technique will streamline your work. Practice helps you develop intuition for selecting the best approach, making problem-solving more efficient over time.

Breaking Down Mathematical Exercises

Approaching complex tasks requires breaking them into smaller, manageable parts. This method allows for a clear understanding of each element and helps identify the appropriate techniques needed to find solutions. By carefully analyzing each step, you can ensure that nothing is overlooked and that you stay on track throughout the process.

Start by identifying the main goal of the problem and the key relationships involved. Look for patterns and any given information that can be used to simplify the task. Breaking the problem into smaller components allows you to tackle each one individually, leading to a more organized and efficient approach.

It’s also important to keep track of any intermediate steps. Recording your progress ensures that you don’t miss any critical details and allows you to backtrack easily if necessary. This careful process enhances accuracy and makes it easier to double-check your work as you move forward.

Common Mistakes in Mathematical Solutions

Even experienced problem-solvers can make errors when working through complex tasks. These mistakes often arise from small oversights, misinterpretations, or rushed steps. Identifying common pitfalls is crucial for improving accuracy and avoiding repeated errors. By learning from these missteps, you can develop a more careful and methodical approach.

Misinterpreting the Problem

One of the most frequent mistakes is failing to fully understand what the problem is asking. Skipping over critical details or misreading instructions can lead to incorrect assumptions and flawed calculations. It’s important to read the problem carefully and identify exactly what is required before attempting to solve it.

Skipping Intermediate Steps

Another common error occurs when solvers skip intermediate steps in an attempt to save time. This often leads to incomplete or incorrect results. Each step should be documented to ensure accuracy and to provide a clear path to the final solution. Skipping these steps can also make it difficult to identify where mistakes occurred if the result is incorrect.

Effective Study Tips for Mathematical Success

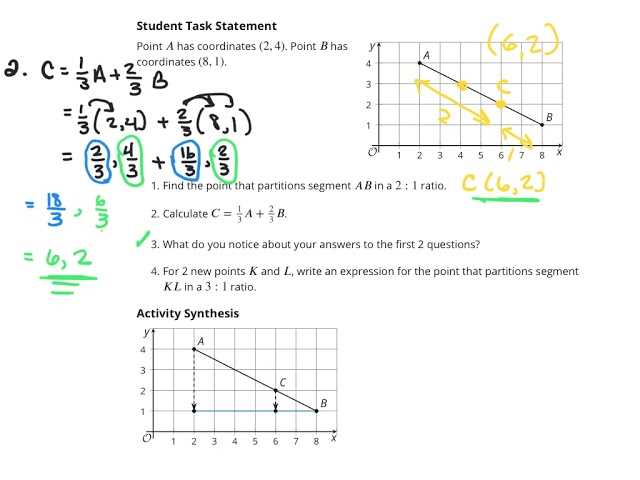
To excel in complex mathematical tasks, it’s important to develop effective study habits and strategies. A structured approach to learning can help reinforce understanding and improve problem-solving skills. By consistently practicing key concepts and following a well-organized study plan, you can achieve better results and deepen your comprehension.

Establish a Consistent Study Routine

Set aside dedicated time each day to focus on problem-solving exercises.
Break down study sessions into manageable chunks to avoid feeling overwhelmed.
Focus on one concept or technique at a time to master it thoroughly before moving on.

Utilize Visual Aids and Diagrams

Draw diagrams or sketches to help visualize complex relationships and shapes.
Use color-coding or labels to highlight key information in problems.
Review example problems to see how concepts are applied in real scenarios.

Practice Regularly and Review Mistakes

Work through various problems to reinforce learning and identify patterns.
Review mistakes carefully to understand where errors occurred and avoid repeating them.
Seek feedback from peers or instructors to gain different perspectives on your approach.

Mathematical Problem-Solving Strategies

When approaching mathematical problems, having a systematic strategy can significantly improve your ability to find accurate solutions. By using proven techniques, you can break down complex tasks into simpler steps, making the process more manageable and less intimidating. A structured approach helps you focus on key concepts, ensuring that each step is tackled with care.

Several strategies can be applied depending on the nature of the problem. These strategies can involve logical reasoning, using visual aids, or applying specific formulas. Each method helps simplify the problem and guides you toward an organized and correct solution.

Strategy	Description	When to Use
Drawing Diagrams	Visualizing the problem can provide clarity, making abstract concepts more concrete.	When working with shapes, angles, or spatial relationships.
Breaking the Problem into Parts	Dividing a complex task into smaller, more manageable components.	When the problem seems overwhelming or involves multiple steps.
Using Algebraic Methods	Applying algebraic formulas or equations to solve for unknowns.	When the problem involves unknown variables or linear relationships.
Testing Different Approaches	Trying different methods to see which yields the best result.	When you’re uncertain about the best strategy or need to confirm results.

Visualizing Mathematical Problems with Diagrams

One of the most effective ways to approach complex problems is by visualizing the situation. Diagrams serve as powerful tools, allowing you to represent relationships and structures clearly, which helps in understanding the problem more thoroughly. By converting abstract concepts into visual formats, you can identify key components, connections, and potential solutions more easily.

Benefits of Using Diagrams

Clarity: Diagrams make complex relationships easier to understand by providing a clear visual representation.
Problem Breakdown: Breaking the problem into manageable parts helps you focus on one element at a time.
Accuracy: Visual aids help reduce the chance of errors, ensuring that all critical components are considered.

Types of Diagrams to Use

Shapes and Figures: Basic geometric shapes like triangles, circles, and squares are useful for illustrating relationships and properties.
Graphs: Graphing can help represent numerical relationships or functions, allowing for easier analysis of trends and solutions.
Coordinate Systems: Plotting points on a coordinate plane provides insight into spatial relationships, distance, and angle measurements.

Utilizing these diagrams during problem-solving can enhance your understanding, clarify concepts, and lead to quicker and more reliable solutions.

Step-by-Step Guide to Solving Mathematical Problems

Approaching complex problems systematically is key to finding the correct solutions. By breaking down each task into manageable steps, you ensure that every aspect is addressed and that nothing is overlooked. This method provides clarity and direction, making even the most challenging problems more approachable.

The following table outlines a step-by-step approach to solving problems effectively. Each phase is designed to guide you through the process, helping you maintain focus and accuracy.

Step	Action	Purpose
Step 1	Understand the problem	Identify key information and what is being asked.
Step 2	Gather relevant formulas and concepts	Ensure you have the right tools and knowledge to approach the problem.
Step 3	Draw a diagram (if applicable)	Visualize the problem to make abstract relationships clearer.
Step 4	Work through the problem	Apply the appropriate methods and calculations, step by step.
Step 5	Review the solution	Check your work for errors and ensure the result makes sense.

By following this structured approach, you can tackle any mathematical problem more confidently and with greater precision.

Understanding Geometric Proofs in Practice

Mastering proofs is a fundamental aspect of solving mathematical problems. By constructing logical arguments based on established principles and definitions, you can demonstrate the truth of various statements. The process involves applying reasoning and systematic steps to support claims, making it an essential skill for any problem solver.

In practical terms, understanding how to approach and construct proofs involves recognizing key concepts, utilizing appropriate methods, and ensuring that each step follows logically from the previous one. It’s a skill that improves with practice, as familiarity with different types of reasoning and strategies helps build confidence and clarity.

Key Components of a Proof

Statements: The claims or assertions you aim to prove or justify within the proof.
Reasons: The justifications for each statement, often derived from definitions, axioms, or previously proven theorems.
Logical Flow: The step-by-step progression that leads from the given information to the conclusion.

Common Proof Strategies

Direct Proof: Starting with known facts and using logical steps to arrive at the desired conclusion.
Proof by Contradiction: Assuming the opposite of what you want to prove and showing that it leads to a contradiction.
Inductive Reasoning: Generalizing from specific examples or cases to make broader conclusions.

By practicing these methods and familiarizing yourself with different types of proofs, you can strengthen your problem-solving abilities and deepen your understanding of mathematical reasoning.

Key Formulas for Solving Mathematical Problems

When tackling mathematical challenges, having a solid grasp of essential formulas is crucial. These equations provide the foundation for solving a wide range of problems, whether you’re calculating areas, volumes, or angles. Understanding and applying these formulas correctly is the key to efficient problem-solving.

Below is a collection of important formulas commonly used in various problem types. Familiarizing yourself with these will help you approach calculations with confidence and clarity.

Basic Area and Perimeter Formulas

Area of a Square: ( A = s^2 ), where ( s ) is the side length.
Area of a Rectangle: ( A = l times w ), where ( l ) is the length and ( w ) is the width.
Perimeter of a Rectangle: ( P = 2l + 2w )
Area of a Triangle: ( A = frac{1}{2} times b times h ), where ( b ) is the base and ( h ) is the height.
Perimeter of a Triangle: ( P = a + b + c ), where ( a ), ( b ), and ( c ) are the lengths of the sides.

Key Volume Formulas

Volume of a Cube: ( V = s^3 ), where ( s ) is the side length.
Volume of a Rectangular Prism: ( V = l times w times h ), where ( l ), ( w ), and ( h ) are the length, width, and height.
Volume of a Cylinder: ( V = pi r^2 h ), where ( r ) is the radius and ( h ) is the height.

Angle and Trigonometric Formulas

Sum of Interior Angles of a Polygon: ( (n – 2) times 180^circ ), where ( n ) is the number of sides.
Pythagorean Theorem: ( a^2 + b^2 = c^2 ), for right-angled triangles.
Sine, Cosine, and Tangent Ratios: ( sin(theta) = frac{text{opposite}}{text{hypotenuse}}, cos(theta) = frac{text{adjacent}}{text{hypotenuse}}, tan(theta) = frac{text{opposite}}{text{adjacent}} ).

By consistently applying these formulas, you’ll develop a deeper understanding of mathematical concepts and improve your problem-solving skills.

Using Geometry Tools for Accuracy

In mathematical problem-solving, precision is key. To ensure that your results are accurate, it is essential to use the right tools for the task. Various instruments help you measure, draw, and calculate with greater exactness, which can make all the difference when working through complex problems.

In this section, we explore some of the most commonly used tools that support precise calculations and measurements. Understanding how and when to use each tool can streamline the process and improve the accuracy of your work.

Essential Tools for Accurate Measurements

Tool	Purpose	Common Uses
Ruler	Measures straight lines and distances	Used for measuring sides of shapes, drawing lines, and calculating lengths
Protractor	Measures angles	Helpful for determining angle measures in various geometric shapes
Compass	Draws circles and arcs	Used for constructing perpendicular bisectors, finding centers of circles, and more
Caliper	Measures the distance between two opposite sides of an object	Useful for measuring thicknesses or distances that cannot be measured directly with a ruler

Why Precision Matters

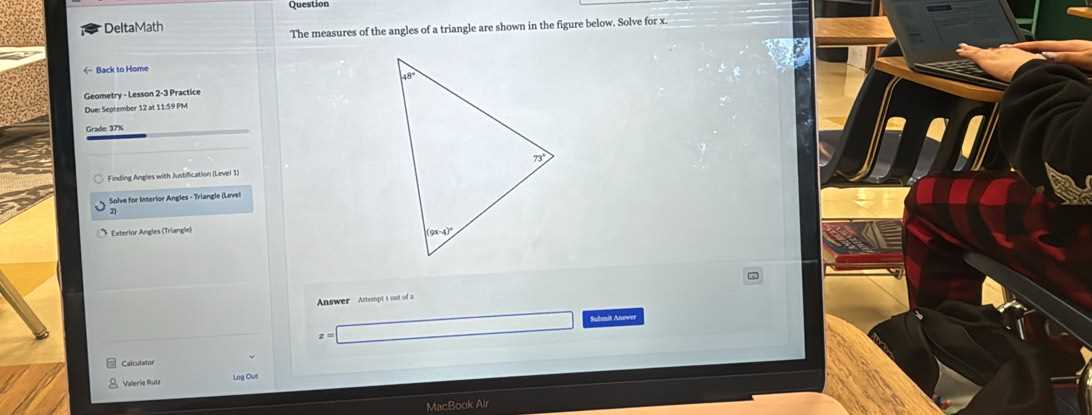
Accuracy in measurement is not only crucial for obtaining correct answers, but it also ensures consistency in results. Even small errors can lead to larger mistakes when working through multi-step problems. By utilizing the appropriate tools, you can minimize errors and work more efficiently.

In addition to physical tools, digital tools such as graphing calculators and software can also enhance accuracy by automating complex calculations and providing visual representations of geometric figures.

By mastering the use of these tools, you will improve both the quality and speed of your work, leading to better results in solving problems and applying mathematical concepts effectively.

How to Check Your Work

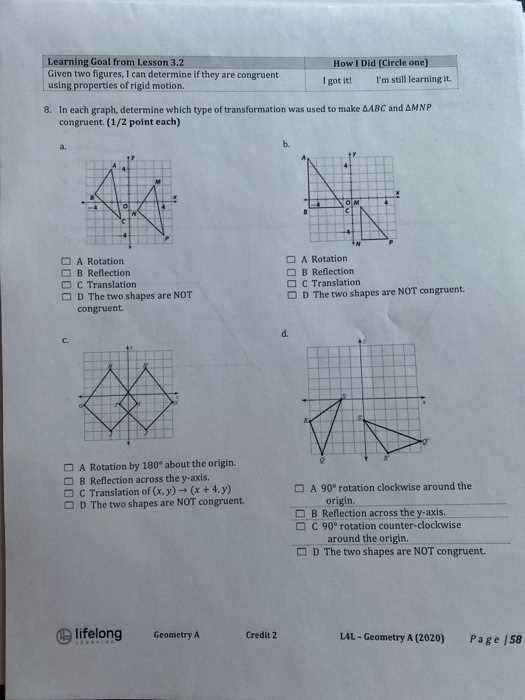
When working through mathematical problems, it’s crucial to ensure that your solutions are correct and precise. Reviewing your steps and results can help you identify errors and improve your problem-solving process. Checking your work is not just about finding mistakes–it’s also a way to reinforce your understanding and build confidence in your answers.

This section will guide you through some effective strategies to verify your calculations and reasoning. By following these steps, you can increase the accuracy of your solutions and reduce the likelihood of making common mistakes.

Steps to Verify Your Work

Review Each Step – Go through your work from the beginning, carefully checking each step of your process. Ensure that all calculations, formulas, and logic are applied correctly.
Double-Check Measurements – If your problem involves measuring or drawing, confirm that all dimensions, angles, and other values are accurate. Small errors in measurement can lead to incorrect answers.
Check for Consistency – Look for consistency in your work. For example, if you’re using a formula, ensure that all variables are consistent with the given information.
Recalculate Key Values – If you’ve performed any complex calculations, it’s a good idea to recalculate key values. This helps catch mistakes that might have been overlooked initially.
Use a Different Method – If possible, try solving the problem using a different approach or method. If both methods yield the same result, you can be more confident in your solution.

Common Tools for Verification

Calculator – A reliable calculator can help you verify complex calculations quickly.
Online Solvers – There are many tools available online that can check solutions for common mathematical problems.
Peer Review – Discuss your work with a classmate or teacher to get a fresh perspective and identify possible mistakes.

By incorporating these verification techniques into your study routine, you’ll not only catch errors but also improve your overall problem-solving skills. With practice, checking your work will become an integral part of your workflow, ensuring that your results are both accurate and reliable.

Lessons Learned from Practice A

When working through a set of exercises, the most valuable takeaways often come from the mistakes we make and the insights we gain from them. By carefully analyzing each problem, we can uncover patterns, refine our methods, and improve our understanding of key concepts. This process is essential not only for mastering specific skills but also for building confidence in solving similar challenges in the future.

In this section, we will explore some of the key lessons learned from completing the practice exercises. These insights will help you identify common pitfalls, better understand core principles, and apply these lessons to future problems.

Key Insights Gained

Attention to Detail – One of the main lessons learned is the importance of attention to detail. Small errors in calculation, measurement, or application of formulas can drastically affect the outcome. Ensuring every step is carefully executed is crucial for accuracy.
Critical Thinking – It’s easy to jump to conclusions based on previous experiences, but each problem can require a fresh approach. Developing critical thinking skills allows for more creative and efficient solutions.
Conceptual Understanding – Many times, the challenge is not in the mechanics of solving a problem, but in truly understanding the underlying concepts. Focusing on how the rules and relationships between elements work can make solving more complex problems easier.
Time Management – Practicing problems within a set time frame helps improve speed and efficiency. Learning how to pace yourself while maintaining accuracy is an essential skill that can be applied across various subjects.

Applying These Lessons

Review Mistakes – Take time to review errors and understand why they occurred. This reflection process is key to not repeating the same mistakes.
Practice Regularly – The more you practice, the more comfortable you will become with the material. This familiarity will lead to faster problem-solving and a deeper understanding.
Test New Approaches – Don’t be afraid to try new strategies. Whether it’s a different method of calculation or a new way to visualize the problem, experimentation can yield more efficient solutions.

By taking the lessons learned from these exercises and applying them to future challenges, you can continuously improve your skills and approach to solving complex problems.

Common Geometry Challenges and Solutions

When solving problems related to shapes, measurements, and spatial reasoning, certain obstacles tend to arise frequently. These challenges can often be traced back to misunderstandings of core concepts or errors in applying mathematical principles. Recognizing these common issues is the first step towards overcoming them, as it allows for targeted strategies to improve accuracy and efficiency.

In this section, we’ll explore some of the most common hurdles faced while working through geometric problems and provide effective solutions for each. By addressing these challenges head-on, students can build a stronger foundation for tackling more complex problems in the future.

Misunderstanding Angle Relationships – One frequent challenge is the confusion between different types of angles, such as complementary, supplementary, and vertical angles. To solve this, it’s essential to memorize key angle properties and practice identifying them within diagrams.
Incorrect Use of Theorems – Many problems require the application of geometric theorems, such as the Pythagorean theorem or properties of similar triangles. A common mistake is misapplying these theorems or using them in the wrong context. The best solution is to thoroughly review the conditions under which each theorem applies, and work through problems that highlight these specific situations.
Forgetting to Label Diagrams – Often, students rush through problems and neglect to label the parts of a diagram. This leads to confusion when solving for unknown variables. The solution is simple: always label diagrams clearly, and refer to these labels when setting up equations or identifying relationships.
Failing to Visualize 3D Shapes – Many students struggle with problems that involve three-dimensional objects, as they can be harder to visualize. A helpful approach is to sketch multiple views of the object or use physical models to better understand its structure and relationships between the parts.
Calculation Errors – Another common issue is making small arithmetic errors, especially when dealing with fractions or complex expressions. To minimize this, double-check all calculations, break down problems into smaller, manageable steps, and use estimation to verify the plausibility of the result.

By focusing on these common challenges and their corresponding solutions, students can strengthen their problem-solving skills and approach geometric problems with more confidence and clarity.

Preparing for Quizzes and Tests

Effective preparation for assessments involving shapes, angles, and measurements requires more than just reviewing notes. It’s about developing a solid understanding of key principles and practicing problem-solving techniques that allow for quick, accurate decision-making under timed conditions. Whether you are facing a quiz or a more comprehensive exam, a structured approach to studying can significantly boost your confidence and performance.

In this section, we will discuss strategies to help you prepare efficiently for quizzes and tests on topics related to spatial reasoning and mathematical reasoning. These methods will not only help you recall formulas and theorems but also ensure that you can apply them to solve problems successfully during the exam.

Review Key Concepts and Theorems

Start by identifying the most important topics covered in your course and focus your attention on understanding the core concepts. This includes reviewing key formulas, theorems, and their applications. Make sure you are comfortable with the following:

Fundamental properties of shapes – Knowing how to classify and apply properties of common figures such as triangles, quadrilaterals, and circles is crucial.
Essential theorems – Be prepared to use well-known theorems like the Pythagorean theorem, properties of parallel lines, and rules for calculating area and volume.
Relationships between angles – Understand concepts like complementary, supplementary, and vertical angles, and how to use them to solve problems.

Practice Problem-Solving Under Timed Conditions

One of the best ways to prepare for an exam is to simulate the testing environment. Practice solving problems under timed conditions to build speed and accuracy. Try to work through a variety of problems, including those that require multi-step solutions, as they are often the most challenging. Focus on:

Solving different types of problems – Include both conceptual questions and numerical ones that test your ability to apply formulas.
Reviewing past quizzes – If available, go over previous quizzes and tests to identify common question patterns and areas where you may need further review.
Double-checking your work – Develop the habit of reviewing your answers before submitting them to catch any mistakes you might have overlooked during the first pass.

By reinforcing your understanding of key principles and consistently practicing under test-like conditions, you’ll be well-equipped to tackle any challenge that comes your way on quiz or test day.

Improving Your Skills Over Time

Mastering mathematical concepts that involve shapes, sizes, and spatial reasoning is a gradual process. Over time, consistent effort and focused practice will lead to greater proficiency and confidence. Improving your skills in this area requires more than just understanding basic principles; it involves developing the ability to apply these principles to a variety of problems, refine your problem-solving strategies, and build on your knowledge continuously.

In this section, we’ll explore strategies for ongoing improvement and how to stay motivated as you strengthen your abilities. Whether you are aiming to perform better in exams or simply deepen your understanding, following a systematic approach will ensure steady progress.

1. Build a Solid Foundation

Before advancing to more complex topics, it’s essential to have a strong grasp of the fundamentals. Revisit basic concepts regularly to reinforce your knowledge. This foundational understanding provides a strong base for tackling more advanced problems later. Consider the following tips:

Review basic formulas – Ensure you understand and can recall key formulas like those for calculating area, perimeter, and volume of various shapes.
Understand core properties – Make sure you can identify the properties of common shapes such as triangles, circles, and polygons, and understand their geometric relationships.
Visualize concepts – Practice drawing shapes, diagrams, and graphs to visualize relationships and better understand the geometric properties at play.

2. Practice Regularly and Review Mistakes

Continuous practice is vital for improvement. The more problems you solve, the more you learn to recognize patterns and techniques that help you find solutions quickly and accurately. Also, focus on analyzing mistakes and understanding why they occurred. This reflection process helps avoid repeating the same errors. Some key strategies include:

Work through different types of problems – Practice a variety of problem types to strengthen your adaptability and problem-solving skills.
Set specific goals – Challenge yourself to master one concept or type of problem each week.
Review and learn from errors – After completing exercises or quizzes, go over any mistakes, understand the reasons behind them, and avoid similar errors in the future.

By consistently reinforcing your foundation and practicing regularly, you’ll notice steady improvements in your understanding and performance over time. This incremental progress will allow you to tackle more complex topics with confidence and skill.

Reviewing Fundamentals

A strong understanding of basic concepts is essential for success in more advanced topics. By revisiting core principles and practicing their application, students can build a solid foundation for tackling increasingly complex challenges. This section aims to help reinforce key ideas and strengthen your ability to approach problems with confidence and clarity.

Whether you’re reviewing for an assessment or simply reinforcing your knowledge, understanding fundamental principles is crucial. The following are some of the main concepts to focus on as you refresh your skills:

Key Concepts to Review

Concept	Description
Shapes and Properties	Familiarize yourself with the characteristics of basic shapes, such as triangles, circles, squares, and rectangles. Knowing their properties helps solve problems more effectively.
Formulas	Ensure you have the essential formulas memorized, like those for calculating area, perimeter, surface area, and volume for different objects.
Angles and Relationships	Understand the various types of angles (acute, obtuse, right) and their relationships within geometric figures (e.g., complementary and supplementary angles).
Symmetry	Review the concept of symmetry in different shapes and how it can be used to solve problems related to congruence and transformations.

Strategies for Effective Review

To fully grasp and retain the basics, it is important to regularly revisit the material and apply it in different contexts. Here are a few strategies that can help:

Practice problems – Work through problems that focus on basic concepts to build fluency.
Create diagrams – Drawing diagrams can help visualize relationships between different shapes and the properties they exhibit.
Teach the material – Explaining concepts to someone else can reinforce your own understanding.
Use resources – Leverage textbooks, online tools, and videos to clarify any areas of confusion and deepen your understanding.

By reviewing these fundamental concepts, you will build a strong mathematical foundation that will serve you well as you progress to more advanced topics. Regular practice and active engagement with the material are key to mastering these basics and improving your overall problem-solving abilities.