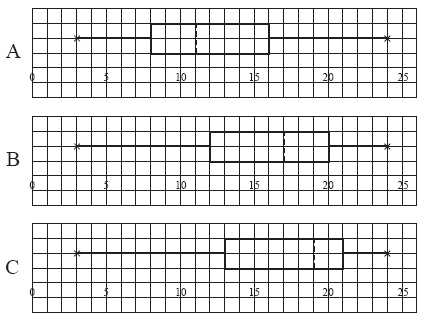
When preparing for assessments involving data visualization techniques, it’s essential to understand the key methods used to represent and analyze numerical information. These techniques help in simplifying complex data, allowing you to identify trends, compare distributions, and detect outliers with ease.
One of the most effective tools in this field is a graphical representation that highlights the spread and central tendency of data. It provides a clear picture of how data points are distributed across different ranges, making it easier to draw conclusions based on visual cues rather than raw numbers.
To succeed in these types of tasks, you need to be familiar with various representations and understand how to interpret the values they present. Whether you’re asked to analyze the distribution of data or assess the variation within a set, mastering these visual tools will give you the confidence needed to tackle any related challenges.
Understanding Data Visualization for Assessments
In many assessments, visual representations of data play a crucial role in helping you understand complex numerical information. These graphical tools allow you to see key patterns, distributions, and variations within a dataset, making it easier to analyze results and draw conclusions.
Key Components to Focus On
To effectively interpret visual data representations, it’s important to understand the various components that are commonly used to convey information. These elements include:
- Median – the middle value that divides the data into two equal halves.
- Quartiles – values that divide the data into quarters, providing insight into the spread.
- Range – the difference between the maximum and minimum values.
- Outliers – values that fall significantly outside the expected range, indicating unusual data points.
How to Interpret the Information

Interpreting these graphs involves recognizing how data is distributed and what that distribution reveals. Key aspects to pay attention to include:
- Identifying the central tendency of the data, which shows where the majority of data points are clustered.
- Understanding the spread of data, which gives insights into its variability.
- Detecting any outliers, which can indicate significant anomalies or important trends.
By familiarizing yourself with these elements, you will be better prepared to analyze and respond to tasks involving visual data representations in your assessments.
Key Concepts in Data Visualization Analysis

In analyzing data through graphical representations, it’s essential to focus on several key concepts that provide valuable insights into how information is distributed. These concepts allow you to evaluate data efficiently, identify patterns, and interpret the underlying structure of the dataset.
Here are the core elements that should be understood when performing analysis:
| Concept | Description |
|---|---|
| Median | The middle value that divides the dataset into two equal halves, representing the center of the distribution. |
| Quartiles | The values that divide the dataset into four equal parts, giving insight into how the data is spread across different ranges. |
| Range | The difference between the maximum and minimum values, showing the overall span of the data. |
| Interquartile Range (IQR) | The range between the first and third quartiles, providing a measure of data spread while excluding outliers. |
| Outliers | Data points that are significantly higher or lower than most others, indicating unusual or extreme values. |
Understanding these concepts is vital for correctly interpreting graphical representations, which in turn will enable you to draw accurate conclusions from the data and better understand the results of any analysis. Each element provides a unique perspective on the dataset, helping to highlight trends and detect any anomalies within the values presented.
Common Data Visualization Problems in Assessments
In assessments that involve graphical representations, you will often encounter tasks that require you to analyze data and extract key insights from visual displays. These problems typically test your ability to interpret values, identify patterns, and detect any anomalies within the dataset. Understanding the common types of problems that arise can help you better prepare for such tasks.
Some of the most frequently encountered challenges in these assessments include:
- Identifying the Median – Determine the central value of the dataset and understand its significance in terms of data distribution.
- Interpreting Quartiles – Find the first, second, and third quartiles, and explain what each quartile represents in the data set.
- Calculating the Range – Calculate the difference between the highest and lowest values to assess the spread of the data.
- Recognizing Outliers – Spot values that deviate significantly from the rest of the data, indicating potential anomalies or important outliers.
- Comparing Distributions – Compare multiple sets of data to assess their similarities, differences, or any trends that may appear in their graphical representations.
Being able to address these types of tasks accurately is crucial for succeeding in any assessment that includes visual data analysis. With proper practice, you will gain confidence in interpreting and solving these challenges effectively.
How to Interpret Data Visualizations
Interpreting visual representations of data involves understanding the key elements that reveal important information about the dataset. These graphical tools help you identify trends, assess variability, and detect anomalies, all of which are critical for accurate analysis. By learning how to interpret these visual cues, you can draw meaningful conclusions from complex data.
Here’s how to break down the key components when interpreting such graphs:
| Element | What to Look For |
|---|---|
| Median | The middle value that divides the dataset in half, representing the center of the distribution. |
| Quartiles | Values that divide the data into quarters, showing how the dataset is spread out across different ranges. |
| Range | The difference between the highest and lowest values, giving an indication of the data’s overall spread. |
| Interquartile Range (IQR) | The difference between the first and third quartiles, representing the middle 50% of the data. |
| Outliers | Data points that fall outside the expected range, often indicating unusual or extreme values. |
By focusing on these key aspects, you can gain a deeper understanding of how the data behaves and make more informed decisions based on your analysis.
Step-by-Step Guide to Data Visualization Calculations
To effectively interpret data through graphical displays, it’s essential to follow a clear process for calculating the key values that define the distribution and spread. This step-by-step guide will walk you through the essential calculations needed to create a comprehensive visual representation of a dataset.
Follow these steps to perform the necessary calculations:
- Sort the Data: Begin by organizing the data in ascending order from the smallest to the largest value.
- Find the Median: Locate the middle value of the dataset. If there is an even number of data points, calculate the average of the two middle values.
- Determine Quartiles:
- First Quartile (Q1) – The median of the lower half of the data, marking the 25th percentile.
- Third Quartile (Q3) – The median of the upper half of the data, marking the 75th percentile.
- Calculate the Interquartile Range (IQR): Subtract the first quartile (Q1) from the third quartile (Q3) to determine the spread of the middle 50% of the data.
- Identify Outliers: Any data points that fall below Q1 – 1.5 * IQR or above Q3 + 1.5 * IQR are considered outliers.
- Determine the Range: Subtract the smallest value from the largest value in the dataset to find the overall spread.
By following these steps, you can accurately calculate the key values that help you analyze the structure of a dataset and represent it visually. These calculations provide essential insights into the data’s central tendency, variability, and any potential anomalies present within the dataset.
Frequently Asked Data Visualization Problems
When preparing for tasks involving graphical representations of data, there are several common types of problems that often appear. These problems typically test your ability to analyze the distribution, central tendency, and spread of the data. Understanding these frequent challenges can help you feel more confident when approaching similar questions.
Key Topics to Focus On
- How to calculate the median: You may be asked to determine the middle value of a dataset, particularly when working with an odd or even number of data points.
- Understanding quartiles: Tasks often require finding the first, second, or third quartiles, helping to break down the data into meaningful segments.
- Outlier detection: Recognizing values that deviate significantly from the rest of the dataset is a key aspect of many problems.
- Data range calculation: You may need to find the difference between the highest and lowest values, helping to determine the overall spread of the data.
- Interpreting the spread of data: Problems may involve analyzing the range between quartiles or the spread of values across the dataset.
Practical Tips for Solving Problems
- Pay attention to the scale: Always be mindful of how the data is represented visually, as this can affect your interpretation.
- Don’t overlook outliers: These extreme values often carry important implications and can dramatically change the interpretation of the data.
- Check for symmetry: Understanding whether the data distribution is symmetrical or skewed can help with drawing conclusions about the dataset.
By focusing on these common areas, you can improve your ability to solve problems related to graphical data analysis and perform well in related tasks.
Common Mistakes in Data Visualization Problems
When working with graphical representations of data, it’s easy to make certain mistakes that can skew the analysis or lead to incorrect conclusions. These errors often stem from misunderstanding the underlying principles or misinterpreting key values that define the data’s distribution. Recognizing these pitfalls is essential for accurate data analysis and interpretation.
Frequent Errors to Avoid
- Misidentifying the Median: The middle value of the dataset should be carefully determined, especially in datasets with an even number of points. Confusing the median with the mean is a common mistake.
- Incorrect Quartile Calculations: Failure to divide the dataset properly when calculating quartiles can result in misleading representations of the data’s spread.
- Overlooking Outliers: Outliers often have a significant impact on the interpretation of the data but can easily be missed or ignored, leading to incorrect analysis.
- Confusing Range with Interquartile Range: The range represents the total spread from the smallest to the largest value, while the interquartile range focuses only on the spread of the central 50% of the data.
- Misinterpreting Data Symmetry: Assuming that the data is evenly distributed without checking for skewness can result in false conclusions about the nature of the dataset.
How to Avoid These Mistakes
- Double-check Your Calculations: Always verify your calculations for the median, quartiles, and range to ensure accuracy before interpreting the data.
- Focus on Data Distribution: Pay attention to whether the data is symmetric or skewed, as this can provide insight into the underlying trends and shape your conclusions.
- Examine Outliers Carefully: Outliers should not be dismissed but rather examined for their impact on the data’s overall trends.
By being mindful of these common mistakes, you can improve your ability to analyze data accurately and make well-informed decisions based on your findings.
How to Identify Outliers in Box Plots
Outliers are data points that stand out significantly from the rest of the values in a dataset. Identifying them is crucial for accurate analysis, as these unusual points can indicate errors, variability, or unique characteristics in the data. In the context of graphical representations, these outliers are typically located away from the central group of values, making them easy to spot once the overall distribution is understood.
The identification of outliers in graphical representations involves several key components. The first step is to examine the range of values and compare them against a defined threshold that separates typical data from extremes. Often, this threshold is based on the interquartile range, a measure of statistical spread. Points that fall far above or below the established limits are considered potential outliers.
| Measure | Calculation | Definition |
|---|---|---|
| Upper Limit | Q3 + 1.5 * IQR | Any point above this value is considered an outlier. |
| Lower Limit | Q1 – 1.5 * IQR | Any point below this value is considered an outlier. |
| IQR (Interquartile Range) | Q3 – Q1 | Range between the 25th and 75th percentiles. |
In practice, the identification process involves calculating these limits and marking points that lie outside of them. These extreme values are then carefully reviewed to determine whether they represent genuine outliers or if they are simply anomalies caused by errors or other factors in data collection.
Box Plot vs Histogram: Key Differences
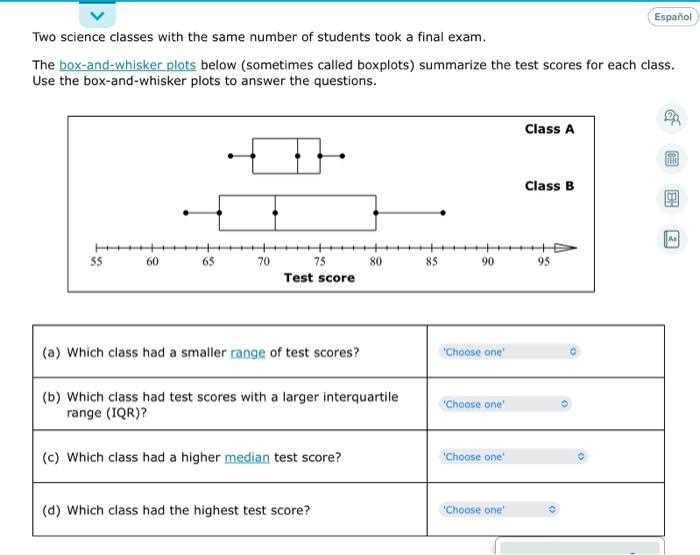
Both graphical tools are used to display the distribution of data, but they offer distinct insights. One focuses on showing the spread and central tendency of a dataset, while the other highlights the frequency of different ranges of values. While both serve the purpose of visualizing data, their methods and the types of information they convey differ significantly.
Box representations provide a summary of the data’s spread, including its central tendency, variability, and potential outliers. It offers a concise way to view the overall distribution without getting into the granular details of individual value frequencies. In contrast, histograms focus more on the frequency distribution, providing a detailed view of how values are distributed across different intervals or bins.
Box representations excel in showcasing key statistical metrics such as the median, quartiles, and potential extreme points. This makes them particularly useful for comparing multiple datasets at once. On the other hand, histograms are better suited for understanding the shape of the data distribution, highlighting patterns like skewness, modality, and the concentration of values.
Preparing for Box Plot Exam Questions
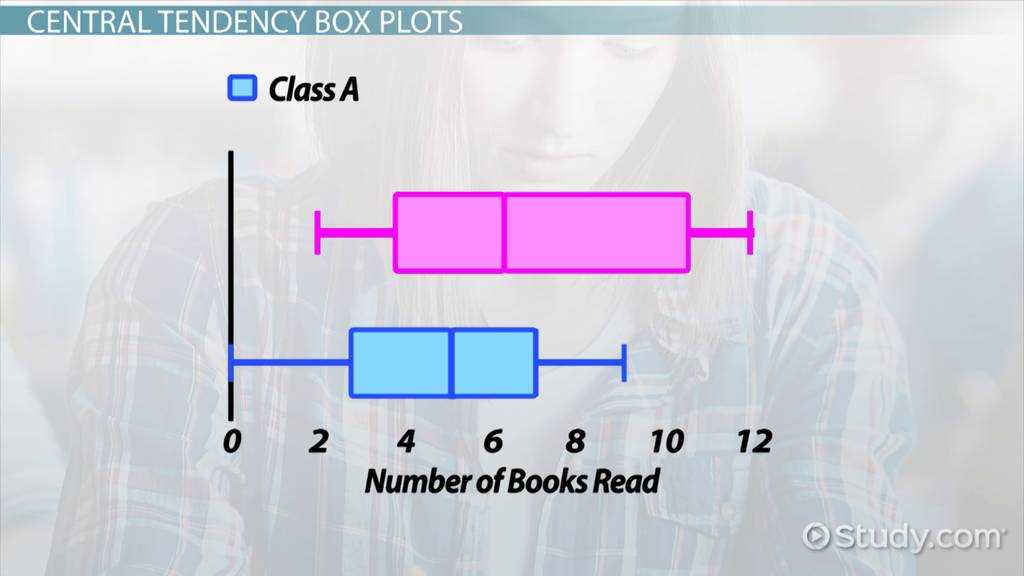
Preparing for assessments that focus on data visualization requires a solid understanding of how to interpret and analyze graphical representations of data. To succeed, one must become familiar with the key components of these visuals, how to extract meaningful insights from them, and how to apply statistical principles when making comparisons or drawing conclusions.
A strong foundation in understanding data distribution is essential, as many questions will require identifying central tendencies, spreads, and outliers. Practice interpreting various datasets and recognizing patterns. Ensure you are comfortable with interpreting the key markers such as quartiles, medians, and extremes, and understand their significance in the context of the overall dataset.
Additionally, it’s helpful to practice comparing different datasets. Being able to quickly assess relative differences in range, skewness, and concentration is an invaluable skill for tackling more complex questions. Developing a clear strategy for approaching such visual tasks will significantly improve accuracy and confidence during evaluations.
Practice Questions for Box Plot Exams
To master the interpretation of graphical representations of data, it’s important to regularly practice with various tasks that challenge your ability to identify key trends, outliers, and relationships. Working through practice scenarios will help you sharpen your analytical skills and become more efficient at interpreting different data sets under exam conditions.
Common Practice Tasks
- Identify the median, quartiles, and range from a given graph.
- Determine if there are any outliers in the dataset and explain their significance.
- Compare two or more datasets and describe their central tendencies and spreads.
- Interpret the skewness of the data based on visual representation.
- Analyze the concentration of data points and describe its implications.
Advanced Practice Problems
- Given a set of multiple visuals, explain the differences in spread and central tendency.
- Based on the graph, predict potential causes for extreme data points and suggest ways to handle them in analysis.
- Evaluate a distribution’s symmetry and discuss how this affects statistical analysis.
- Interpret how a change in the data set affects the overall representation.
Real-World Applications of Box Plots
Visualizing data distribution is a powerful tool for decision-making in various industries. By summarizing key statistical metrics, these visualizations allow professionals to quickly assess the spread, central tendency, and potential outliers within large datasets. This ability to interpret data in a concise format is invaluable in fields ranging from finance to healthcare.
In business and finance, these visuals are used to assess market trends, identify investment risks, and analyze stock performance. Investors rely on such representations to understand volatility and make informed decisions based on the overall spread and behavior of asset prices.
In healthcare, they assist researchers in analyzing patient data, identifying unusual cases, and ensuring the accuracy of clinical trials. By visualizing the distribution of various health metrics, professionals can detect trends and make data-driven recommendations for treatment plans or interventions.
In education, they help to visualize student performance across different metrics, such as exam scores or graduation rates. Educational institutions use these tools to detect outliers and address discrepancies in student achievement, guiding improvements in teaching methods and curriculum design.
Overall, these methods are essential in any field where data-driven decisions are made. The ability to quickly interpret the spread and variability of data allows for more effective analysis and better decision-making strategies.
Tips for Solving Box Plot Problems Quickly

Solving problems related to data visualizations requires both speed and accuracy. With the right approach, you can quickly extract the necessary information and make informed decisions. Focus on key steps that help you understand the distribution and identify critical elements like central tendency, variability, and outliers.
Key Steps to Follow
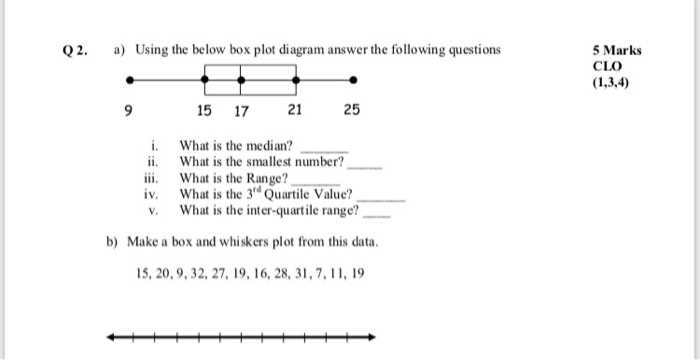
- Start by identifying the median, quartiles, and range, as these are the most crucial components.
- Look for any values that lie outside the normal range–these are often outliers that may require further attention.
- Always compare the spread of values to check for symmetry or skewness in the dataset.
- Make sure to interpret the scale of the graph correctly to avoid misreading the data.
Time-Saving Strategies
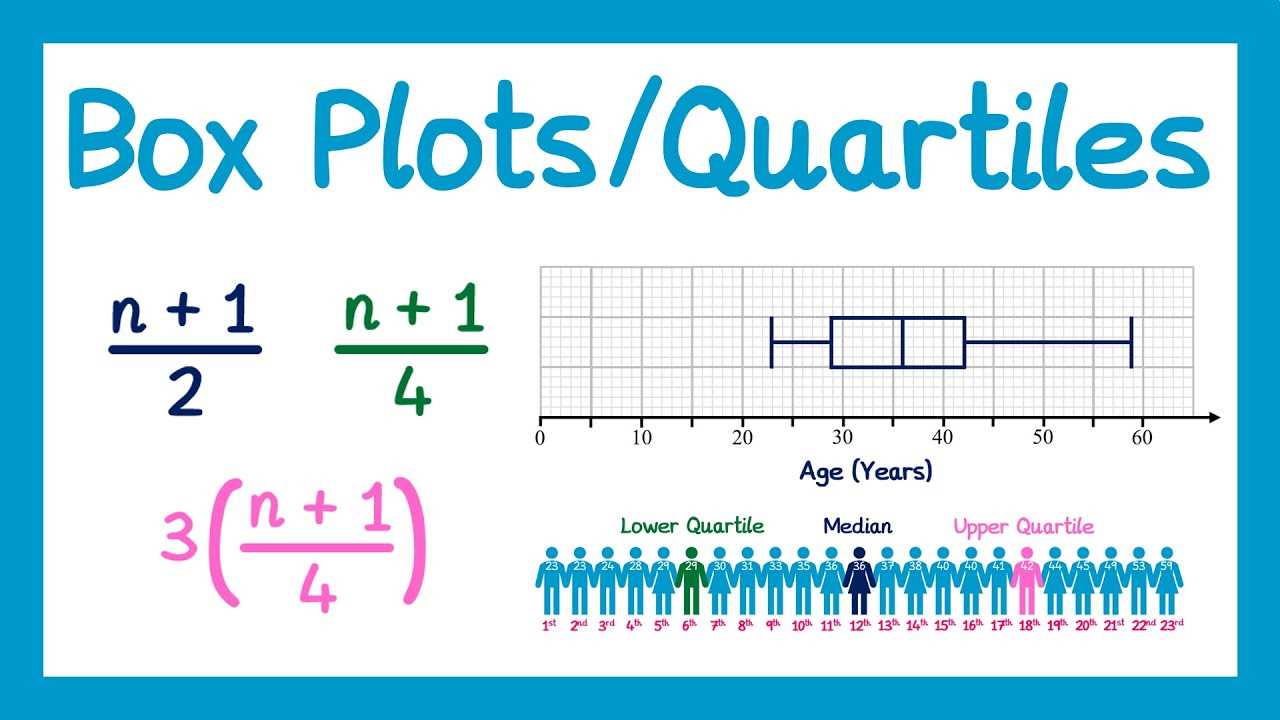
- Familiarize yourself with common patterns so you can quickly recognize them in the data.
- Practice identifying outliers without focusing on every individual value–focus on the extremes.
- Use shortcuts to identify the interquartile range and standard deviations to quickly assess spread.
- Stay calm and approach each problem systematically to avoid rushing through details.
How to Analyze Box Plot Variability
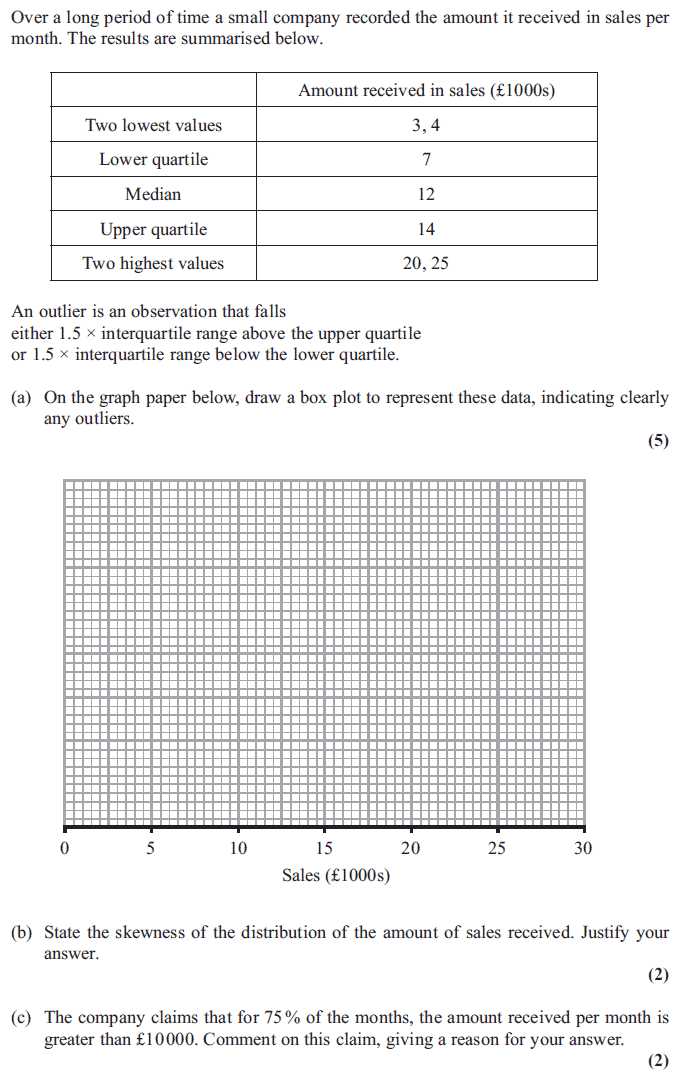
Understanding the variability within a dataset is essential for identifying patterns, trends, and outliers. Analyzing how data points spread around a central value can provide insights into the consistency or diversity of the dataset. By examining certain key features, you can gain a deeper understanding of how the data behaves and make more informed decisions.
Key Factors to Assess
- Range: The total spread from the smallest to the largest value. A wider range indicates more variability in the data.
- Interquartile Range (IQR): The distance between the first quartile (Q1) and the third quartile (Q3). This measures the spread of the middle 50% of the data, giving a clearer picture of variability than the total range.
- Outliers: Data points that lie outside the normal range, often beyond 1.5 times the IQR from the quartiles. These can indicate unusual observations that may significantly affect variability.
Assessing Data Distribution
Symmetry is another important aspect when analyzing variability. A symmetric distribution suggests that data points are evenly distributed around the central value, leading to lower variability. On the other hand, skewness can indicate higher variability on one side of the distribution. The larger the spread from the median to either end, the greater the variability in that part of the data.
Advanced Box Plot Exam Topics
When delving deeper into data visualizations, understanding more complex concepts becomes essential for thorough analysis. These advanced topics not only help you interpret more detailed visual representations, but they also prepare you to handle a broader range of problems. Mastering these concepts will enhance your ability to analyze data distributions critically and make more informed decisions based on statistical principles.
One advanced concept involves comparing multiple distributions simultaneously. This requires an understanding of how to identify subtle differences between datasets, such as shifts in central tendency, changes in variability, and the impact of outliers. Mastering this technique enables you to draw more sophisticated conclusions when dealing with real-world data.
Another important aspect is identifying and addressing skewness. Understanding how skewness affects the interpretation of data and adjusting for it accordingly is crucial in advanced analysis. Additionally, mastering the use of weighted measures and interpreting data through different percentiles adds depth to the analysis of data trends.
Box Plot Tricks for Exam Success
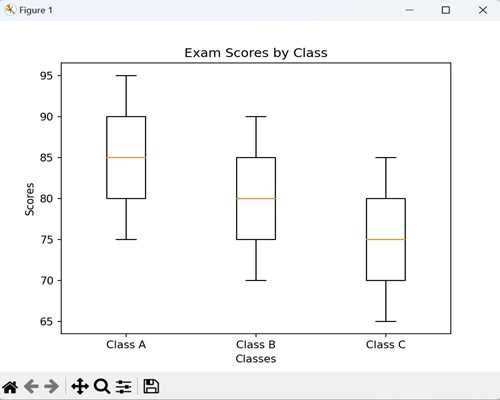
To excel in assessments involving data visualizations, it’s important to develop efficient strategies for interpreting and analyzing graphical representations. By mastering key techniques, you can quickly extract valuable insights from any dataset. These tricks will help you approach problems with confidence, saving time and improving accuracy in your analysis.
Focus on Key Components: Always begin by identifying the central value, quartiles, and potential outliers. Understanding these fundamental aspects is crucial for quickly evaluating the spread and tendencies of the data.
Look for Symmetry or Skewness: Pay attention to whether the distribution is symmetric or skewed. This can help you quickly identify whether the data follows a normal distribution or has significant deviations that might affect further analysis.
Use the IQR Rule for Outliers: The interquartile range (IQR) is one of the most effective ways to identify outliers. Quickly calculating 1.5 times the IQR and checking for data points beyond this range will help you spot extreme values with minimal effort.
Practice with Real Data: Familiarize yourself with real-world datasets to build intuition about typical distributions, spread, and patterns. The more you practice, the faster you’ll become at recognizing key features of any visualization.