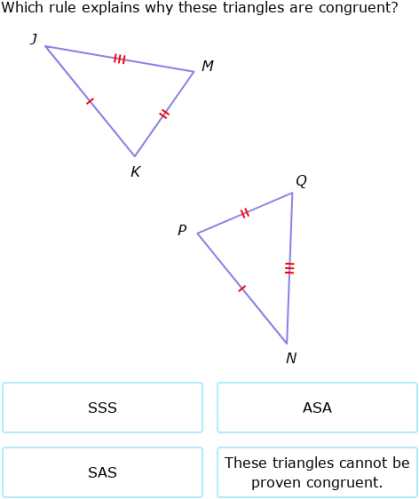
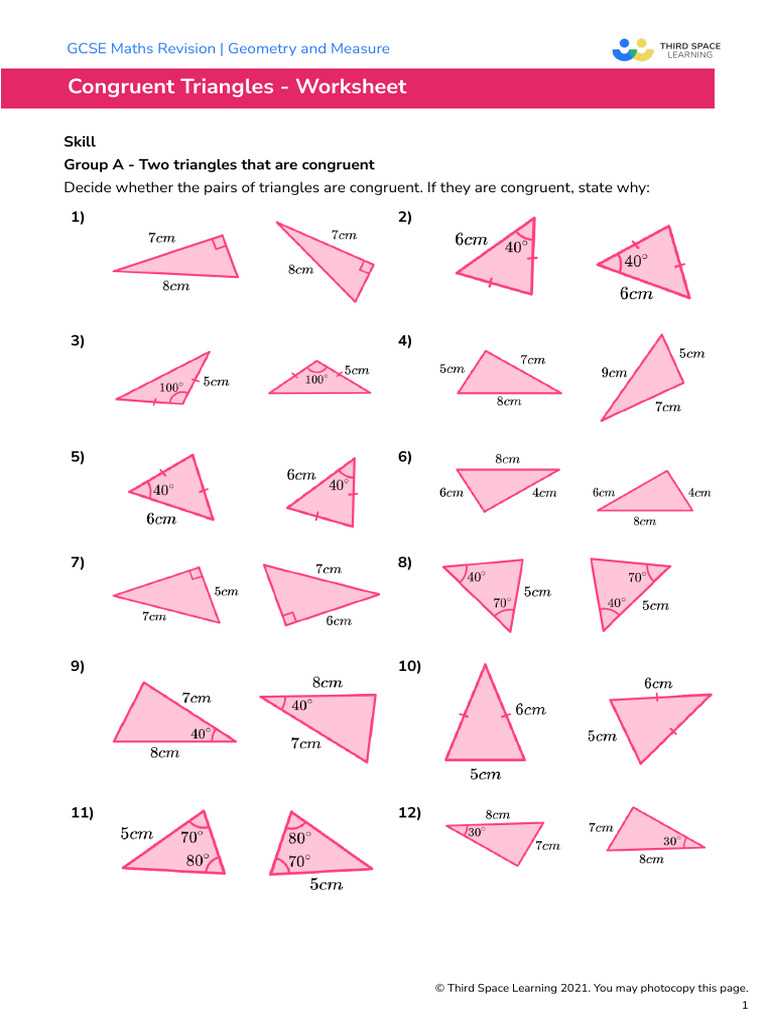
Geometry involves a range of fundamental principles that are essential for solving various problems. One of the core topics focuses on comparing shapes based on their properties and determining whether they share identical measurements and structures. Mastering this concept is crucial for students aiming to succeed in their studies.
In this section, we will explore various problems related to shape comparisons, providing effective methods and strategies to solve them. By examining typical exercises, you will gain a deeper understanding of how to apply theoretical knowledge to practical situations. Through clear explanations and helpful tips, you can enhance your problem-solving skills in geometry.
Congruent Shapes Problems and Solutions
Mastering the identification and comparison of similar geometric figures is an essential skill in geometry. In this section, we will discuss a variety of typical challenges involving shape comparison, focusing on identifying when two figures match in size and form. By practicing these types of problems, you will strengthen your understanding of key concepts and improve your ability to apply them in different contexts.
Identifying Matching Figures
One of the first tasks is recognizing when two figures are identical in size and shape. This involves checking whether their sides and angles correspond precisely, which can be proven through various methods such as measurement or calculation. Understanding these methods allows you to determine if the figures are indeed equal in all aspects.
Step-by-Step Solution Techniques
Once you’ve identified that the figures are identical, it’s time to apply specific techniques to demonstrate the match. These steps typically involve confirming that corresponding parts align perfectly, using logical proofs or algebraic calculations. By breaking down the process into manageable steps, the solution becomes clearer and more accessible.
Understanding Congruence in Geometry
In geometry, the concept of two shapes being identical in terms of size and form plays a crucial role. It’s essential to know how to compare different figures to determine if they match in every aspect, from their angles to the length of their sides. This process helps in understanding how geometric shapes relate to one another, ensuring that their properties align perfectly.
The concept applies to many areas of geometry, allowing students and professionals alike to classify and manipulate shapes more effectively. Whether working with polygons, circles, or other forms, recognizing when two objects are equal in all respects is a foundational skill that underpins much of geometric reasoning.
| Property | Definition |
|---|---|
| Sides | The corresponding sides of the shapes must be of equal length. |
| Angles | The corresponding angles must be of the same measure. |
| Overall Shape | The shape should be identical in size and orientation, though they may be flipped or rotated. |
Types of Congruent Triangle Theorems
In geometry, there are several key principles that help determine when two figures are identical in size and shape. These rules allow for the comparison of shapes based on specific properties, such as their sides and angles, to prove that they are equal. Understanding these theorems is essential for solving various geometric problems efficiently and accurately.
Each theorem provides a unique method for establishing equality between two shapes. Some focus on comparing side lengths, while others rely on angles or a combination of both. These theorems serve as foundational tools in geometric proofs and calculations, ensuring that relationships between shapes are well-defined.
Common Mistakes in Triangle Congruence
When solving problems related to shape equality, it’s easy to overlook key details that can lead to errors. Many students encounter challenges in determining when two figures are truly identical, often making assumptions based on incomplete information. Understanding where mistakes tend to occur can help avoid these pitfalls and improve overall problem-solving accuracy.
One common mistake is assuming two shapes are equal just because they look similar at first glance. In reality, specific properties need to align exactly, such as the precise measurement of corresponding sides and angles. In other cases, relying on visual comparisons without applying the correct rules can lead to incorrect conclusions.
| Common Mistake | Explanation |
|---|---|
| Assuming similarity means equality | Similarity does not guarantee identical size or shape; equal measurements are required. |
| Overlooking angle differences | Failing to check that corresponding angles match exactly can lead to incorrect results. |
| Misinterpreting side-length conditions | It’s essential to compare all corresponding sides to ensure they are of equal length. |
How to Prove Triangles are Congruent
Proving that two shapes are identical in size and form involves a systematic approach. It’s essential to examine their corresponding parts–sides and angles–and confirm that these measurements align perfectly. This process ensures that the figures meet the criteria for being considered equal, based on geometric properties.
To establish that two shapes are indeed the same, several methods can be used, depending on the information available. By applying specific theorems and carefully analyzing the relationships between the figures, it becomes possible to demonstrate their equality in a structured and logical manner.
Key Proof Methods
There are a few standard methods commonly used in geometry to prove the equality of two figures. The most common involve comparing specific sets of corresponding parts, such as sides and angles, using well-established theorems to confirm the match.
Step-by-Step Approach
The following steps outline the typical process for proving the equality of two figures:
| Step | Action |
|---|---|
| 1 | Identify and label corresponding sides and angles. |
| 2 | Apply appropriate theorems (e.g., SSS, SAS, ASA) based on the known information. |
| 3 | Use logical reasoning to show that all corresponding parts match. |
| 4 | Conclude the proof by confirming that the shapes are equal. |
Key Formulas for Congruent Triangles
In geometry, understanding the fundamental formulas for comparing shapes is essential for solving problems related to their equality. These formulas allow you to establish the necessary conditions that must be met for two figures to be considered identical in size and shape. By applying the right formula, you can determine if two shapes are equal based on their sides and angles.
The following list outlines the key formulas and theorems commonly used to establish the equality of geometric shapes. These principles are critical tools for solving a variety of related problems efficiently.
Commonly Used Formulas
- SSS (Side-Side-Side) Theorem: If all three sides of one figure are equal to the corresponding sides of another, the figures are identical.
- SAS (Side-Angle-Side) Theorem: If two sides and the angle between them in one shape match the corresponding parts of another, the figures are equal.
- ASA (Angle-Side-Angle) Theorem: If two angles and the side between them are equal in both shapes, the figures are identical.
- AAS (Angle-Angle-Side) Theorem: If two angles and a non-included side match between two shapes, they are equal.
When to Apply These Formulas
These formulas are used in different scenarios, depending on the information you are given. For example, when two sides and an angle are provided, the SAS theorem would be applied. Understanding which theorem to use based on the given conditions is crucial for solving problems correctly.
- Determine the known measurements in the problem.
- Select the appropriate theorem based on the available information.
- Apply the theorem and check for equality of the corresponding parts.
- Conclude that the figures are identical when all conditions are met.
Real-World Applications of Congruence

The concept of shape equality plays a crucial role in many fields beyond the classroom. Understanding when two objects match in size and form is essential for solving practical problems in various industries. This principle is used in everything from engineering to architecture, helping to ensure that designs are accurate and functional.
In everyday life, the ability to identify matching shapes helps with tasks ranging from manufacturing products to creating reliable blueprints. Whether it’s in construction, design, or technology, this skill is critical for ensuring that parts fit together precisely and systems function properly.
Applications in Engineering
In engineering, the concept of identical parts is essential for designing machinery and structures. When building mechanical systems, for instance, engineers need to ensure that all parts are precisely matched to avoid malfunctions. Knowing how to verify when parts are equal allows for efficient production and assembly.
Applications in Architecture and Construction
In architecture, matching shapes are vital when creating structural elements that must fit together perfectly. Builders rely on geometric principles to make sure that walls, windows, and doors align correctly. This accuracy ensures both the aesthetic appeal and the structural integrity of buildings.
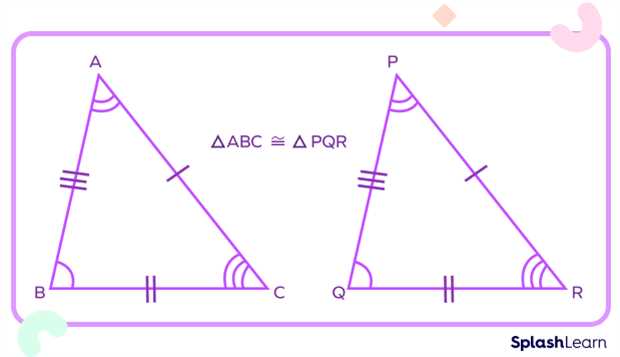
Visualizing Congruent Triangles with Diagrams
Diagrams are a powerful tool for understanding geometric relationships, especially when determining if two shapes are identical. By visually representing these figures, it becomes easier to compare their sides, angles, and overall structure. Visual aids simplify complex concepts, helping students grasp geometric principles more effectively.
When working with geometric shapes, a diagram allows you to clearly identify the corresponding parts of two objects. This visual approach supports the application of theorems and formulas by providing a direct comparison, making it easier to confirm equality between figures.
Benefits of Using Diagrams
One of the key advantages of using diagrams is that they provide a clear, visual reference for identifying corresponding elements. This visual clarity helps to avoid common mistakes and allows for more accurate reasoning. When two shapes are drawn with labeled sides and angles, it becomes simple to apply the appropriate geometric rules and verify their equality.
How to Interpret Diagrams
To interpret a diagram effectively, focus on the following elements:
- Corresponding Sides: Ensure the sides of the two figures match in length.
- Corresponding Angles: Check if the angles between the sides are identical.
- Labeling: Proper labeling helps in easily identifying the matching parts between the two shapes.
By using well-drawn diagrams, you can quickly identify whether the figures are indeed identical, and apply geometric reasoning more effectively to solve problems.
Step-by-Step Guide to Solving Problems
Solving geometric problems efficiently requires a structured approach. By following a logical sequence of steps, you can simplify the process and arrive at accurate solutions. Breaking down the problem into manageable tasks helps to ensure that no detail is overlooked and that you are using the correct methods to reach your conclusion.
This guide outlines a step-by-step method to tackle common geometric challenges, focusing on identifying relationships between shapes, applying appropriate theorems, and verifying the results. By following this approach, you can approach each problem systematically, making it easier to solve and understand.
Step 1: Analyze the Given Information
- Read the problem carefully and identify the known data.
- Label all relevant parts of the figures (sides, angles, etc.).
- Determine which geometric principles might apply to the problem.
Step 2: Apply Relevant Theorems
- Choose the correct theorem based on the given information (e.g., SSS, SAS, ASA).
- Use logical reasoning to apply the theorem to the situation.
- Work through the steps of the theorem to check for equality between the figures.
Step 3: Check for Consistency and Finalize the Solution
- Ensure that all corresponding parts are equal as per the theorem.
- Double-check your work for accuracy in labeling and application of theorems.
- Draw a conclusion based on the comparison and confirm if the shapes are indeed equal.
Frequently Asked Questions About Congruent Triangles
Many people encounter challenges when learning about the equality of geometric shapes. The concepts can seem complex at first, but understanding the basic principles and clarifying common doubts can make the topic much more approachable. This section addresses some of the most frequently asked questions regarding shape equality and aims to provide clear explanations and helpful insights.
What is the Definition of Shape Equality?
Shape equality means that two objects have the same size and form. When two figures are equal, every corresponding side and angle matches exactly. This property is essential when comparing geometric shapes to determine if they are identical or not.
How Can I Prove That Two Figures Are Equal?
- Ensure that the figures match in all corresponding sides and angles.
- Use geometric theorems such as SSS (side-side-side), SAS (side-angle-side), or ASA (angle-side-angle) to establish equality.
- Apply logical reasoning to check that all parts align according to the chosen theorem.
Are There Different Types of Equal Shapes?
- Yes, there are different types of shape equality based on the number and types of parts involved. For example, side-angle-side or angle-side-angle are specific conditions for establishing equality.
- The way the figures are compared (sides or angles) determines the method of proving equality.
Using Congruent Triangles in Proofs
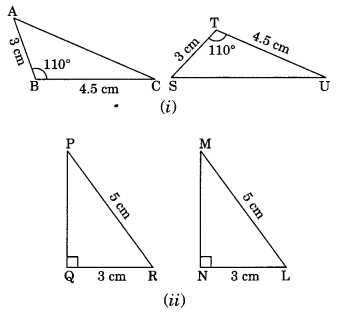
In geometry, proving the equality of shapes is a crucial part of solving problems and establishing relationships between different figures. The ability to demonstrate that two objects share identical properties–whether it be their sides, angles, or other elements–forms the foundation of many geometric proofs. By using equality theorems, we can build logical arguments and arrive at conclusive results.
When proving that two shapes are equal, one common approach involves showing that their parts align according to specific theorems. These steps provide a structured way to justify relationships between different elements within a proof, making the argument more robust and clear. This method is especially useful in both simple and complex geometric proofs.
Key Theorems for Proofs
- SSS (Side-Side-Side): If all three sides of one figure match the corresponding sides of another figure, they are equal.
- SAS (Side-Angle-Side): If two sides and the included angle of one figure match the corresponding parts of another figure, they are equal.
- ASA (Angle-Side-Angle): If two angles and the side between them in one figure match the corresponding parts of another figure, they are equal.
- AAS (Angle-Angle-Side): If two angles and a non-included side of one figure match the corresponding parts of another figure, they are equal.
Steps for Proving Shape Equality
- Identify and label all the parts of the figures involved in the proof (sides, angles, etc.).
- Determine the appropriate theorem (SSS, SAS, ASA, etc.) based on the available information.
- Apply the chosen theorem logically to show that the figures meet the conditions for equality.
- Conclude the proof by demonstrating that the figures are indeed equal, using the results from the theorem.
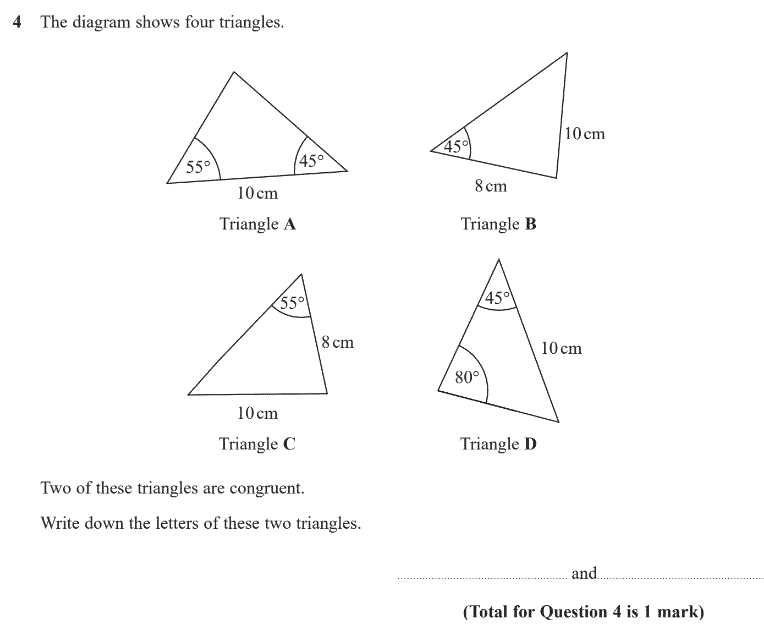
Comparing SSS, SAS, ASA, AAS Theorems
In geometry, various theorems help establish whether two figures are identical in shape and size. These theorems each focus on specific relationships between the sides and angles of the figures involved. Understanding the differences between these methods is crucial for solving problems that require proving shape equality. Each theorem has distinct criteria for determining if two objects match, offering different tools depending on the information available.
The four key theorems–SSS, SAS, ASA, and AAS–are essential for geometric proofs. Although they all serve the same purpose, they apply to different scenarios, depending on what parts of the figures are known to be equal. Here, we will compare and contrast these theorems, highlighting their conditions and when to use each one effectively.
Key Differences Between Theorems
| Theorem | Conditions for Equality | Usage |
|---|---|---|
| SSS | All three sides are equal | Use when all sides of the figures are known to be the same length |
| SAS | Two sides and the included angle are equal | Use when two sides and the angle between them are known to be the same |
| ASA | Two angles and the side between them are equal | Use when two angles and the side in between them are known to be identical |
| AAS | Two angles and a non-included side are equal | Use when two angles and a non-included side are the same between the figures |
When to Use Each Theorem
- SSS: Best used when the lengths of all three sides of both figures are known.
- SAS: Ideal when two sides and the included angle are given.
- ASA: Applied when two angles and the side between them are known to be identical.
- AAS: Suitable for situations where two angles and one non-included side match.
Common Geometry Theorems in Exams

Geometry is a fundamental branch of mathematics, and several theorems are frequently tested in assessments. These theorems serve as the building blocks for solving a wide variety of problems, from determining shape relationships to calculating angles and distances. Understanding the key principles and knowing when to apply them is essential for tackling geometric challenges effectively. In this section, we’ll explore some of the most commonly used theorems in geometric proofs and problem-solving tasks.
Whether dealing with figures in two-dimensional space or working through more complex scenarios, these theorems help students make critical connections. Mastery of these principles can simplify even the most complicated problems. Here, we will look at the theorems most likely to appear in tests and how they help solve common geometric questions.
Preparing for Geometry Assessments
Effective preparation is key to mastering geometric concepts and performing well on assessments. To excel in solving problems related to shape similarity and equality, it’s crucial to develop a strong understanding of key principles and theorems. By focusing on a strategic study plan, students can build the skills needed to approach geometry problems with confidence. Below are some helpful tips to guide your preparation.
- Understand the Theorems: Review fundamental rules, such as those governing side lengths, angles, and relationships between different geometric shapes. Make sure to grasp the logic behind each theorem and how it applies to various problems.
- Practice Problem-Solving: The more problems you solve, the better you’ll understand how to apply these concepts effectively. Practice both basic and more complex scenarios to build confidence and familiarity.
- Focus on Diagrams: Being able to interpret and draw accurate diagrams is crucial in solving problems. Make sure to practice sketching different geometric figures and labeling key components.
- Review Past Assessments: Go over previous practice problems or assessments to identify common question types and recurring concepts. This will help you anticipate what might appear in future tests.
- Seek Help When Needed: If any concepts seem unclear, don’t hesitate to ask for assistance. Whether it’s from a teacher, tutor, or fellow student, clarifying doubts early can prevent confusion later.
By integrating these strategies into your study routine, you’ll be well-equipped to solve even the most challenging problems and perform your best in any geometric assessment.
Tips for Mastering Triangle Congruence
Achieving a deep understanding of the relationships between geometric figures is essential for solving problems effectively. One of the key areas to focus on is the concept of equality in shapes, particularly when proving that two figures are identical in size and form. Mastering the rules and techniques for establishing these relationships can significantly improve problem-solving skills and boost confidence in tackling complex geometric challenges.
1. Know the Key Theorems

Understanding the fundamental principles is the foundation of mastering this topic. Familiarize yourself with the main theorems that establish when two shapes are identical. These include criteria based on side lengths, angles, and their interrelations. Having a solid grasp of these rules will make it easier to recognize when two figures are equal.
2. Visualize and Practice Regularly
Building proficiency requires hands-on practice and frequent engagement with geometric figures. Draw diagrams regularly, label parts accurately, and apply the theorems you’ve learned. Through consistent practice, you’ll gain the confidence to spot key patterns and quickly identify equal shapes in problems.
By focusing on these key areas and incorporating regular practice into your study routine, you’ll be able to master this important concept and improve your geometric reasoning skills overall.
Advanced Topics in Triangle Congruence
As you advance in your study of geometry, you’ll encounter more complex concepts that deepen your understanding of how shapes relate to one another. While basic principles provide the foundation, there are additional topics that explore the nuances of shape equality in greater depth. These concepts are essential for tackling advanced problems and developing a sophisticated understanding of geometric relationships.
1. Transformations and Their Role in Shape Equality
One of the more advanced areas in geometry involves understanding how transformations, such as translations, rotations, and reflections, can be used to prove that two figures are identical. These operations do not change the size or shape of the object, but they change its position or orientation in space. By applying transformations, you can demonstrate the equivalence of shapes in a more dynamic way, offering new tools for solving complex problems.
2. Coordinate Geometry and Proof Techniques
Another advanced topic is the use of coordinate geometry to prove that two figures are equal. By assigning coordinates to key points and using algebraic methods, you can prove that corresponding parts of two shapes are identical. This technique brings an analytical approach to geometric problems, adding precision to the proof process and allowing for more complex cases to be addressed with greater ease.
These advanced topics go beyond basic shape identification and provide powerful techniques for solving higher-level geometric problems. Mastering them will significantly expand your toolkit and prepare you for more challenging mathematical tasks.