Mathematics can often be a challenge for students, especially when it comes to mastering complex concepts. One area that frequently causes difficulty is solving problems that require a deep understanding of geometric relationships and functions. By practicing the fundamental principles, learners can improve their ability to solve problems with confidence and precision.
It is essential to develop a strong grasp of core principles and techniques, such as working with angles, understanding ratios, and applying identities. The key to success lies not just in memorization but in being able to recognize patterns and approach each problem systematically.
By focusing on effective strategies and practicing a variety of problems, students can gain the skills needed to perform well in assessments. This guide aims to provide helpful insights into how to approach various types of tasks, along with solutions that illustrate key methods and tricks for success.
Trigonometric Functions and Their Properties
Mathematical functions that relate angles to specific ratios play a crucial role in solving problems involving circles, waves, and oscillations. Understanding these functions is essential for tackling various challenges in geometry and physics. By grasping their characteristics, one can effectively approach a wide range of tasks that involve angle measures and relationships between sides of triangles.
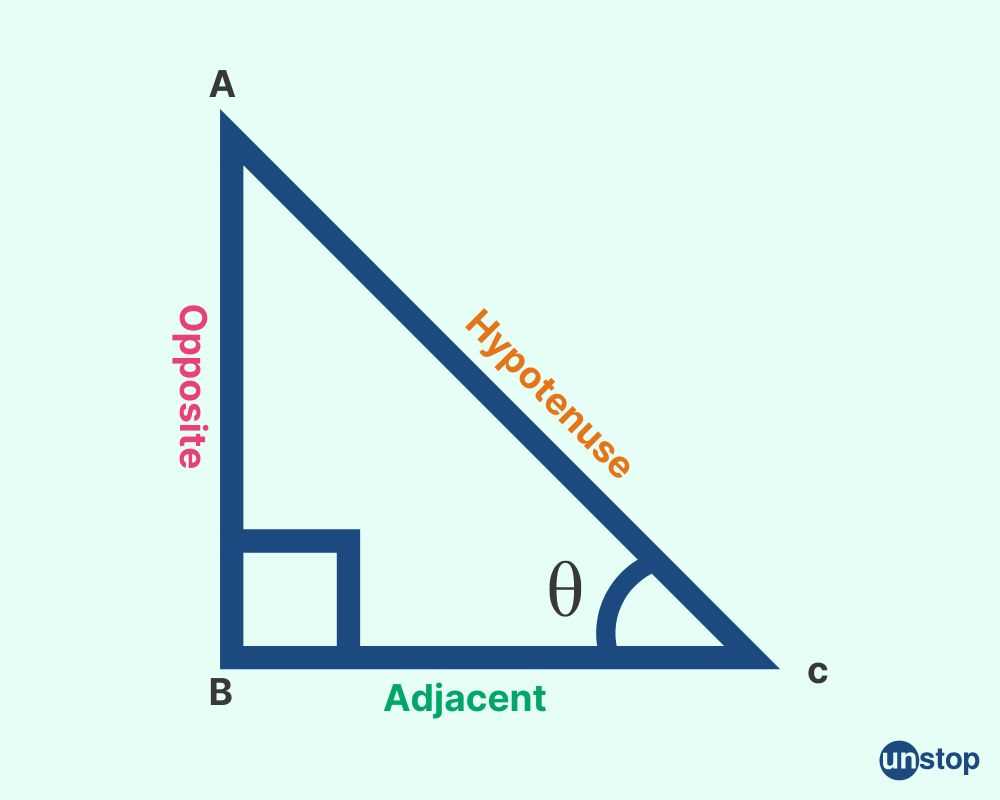
The most commonly used functions in this context are sine, cosine, tangent, secant, cosecant, and cotangent. These functions are not only fundamental in solving geometric problems but also in analyzing periodic behavior in real-world scenarios. Each function has distinct properties that make it useful for different types of calculations.
| Function | Definition | Range | Key Identity |
|---|---|---|---|
| Sine | Opposite side over hypotenuse | -1 to 1 | sin?(?) + cos?(?) = 1 |
| Cosine | Adjacent side over hypotenuse | -1 to 1 | sin?(?) + cos?(?) = 1 |
| Tangent | Opposite side over adjacent side | All real numbers | tan(?) = sin(?) / cos(?) |
| Secant | Hypotenuse over adjacent side | Less than -1 or greater than 1 | sec(?) = 1 / cos(?) |
| Cosecant | Hypotenuse over opposite side | Less than -1 or greater than 1 | csc(?) = 1 / sin(?) |
| Cotangent | Adjacent side over opposite side | All real numbers | cot(?) = 1 / tan(?) |
Each of these functions behaves differently depending on the angle, and understanding their properties allows for accurate problem-solving in both theoretical and applied contexts. With practice, one can learn how to manipulate these functions to simplify complex calculations and solve challenging geometric puzzles effectively.
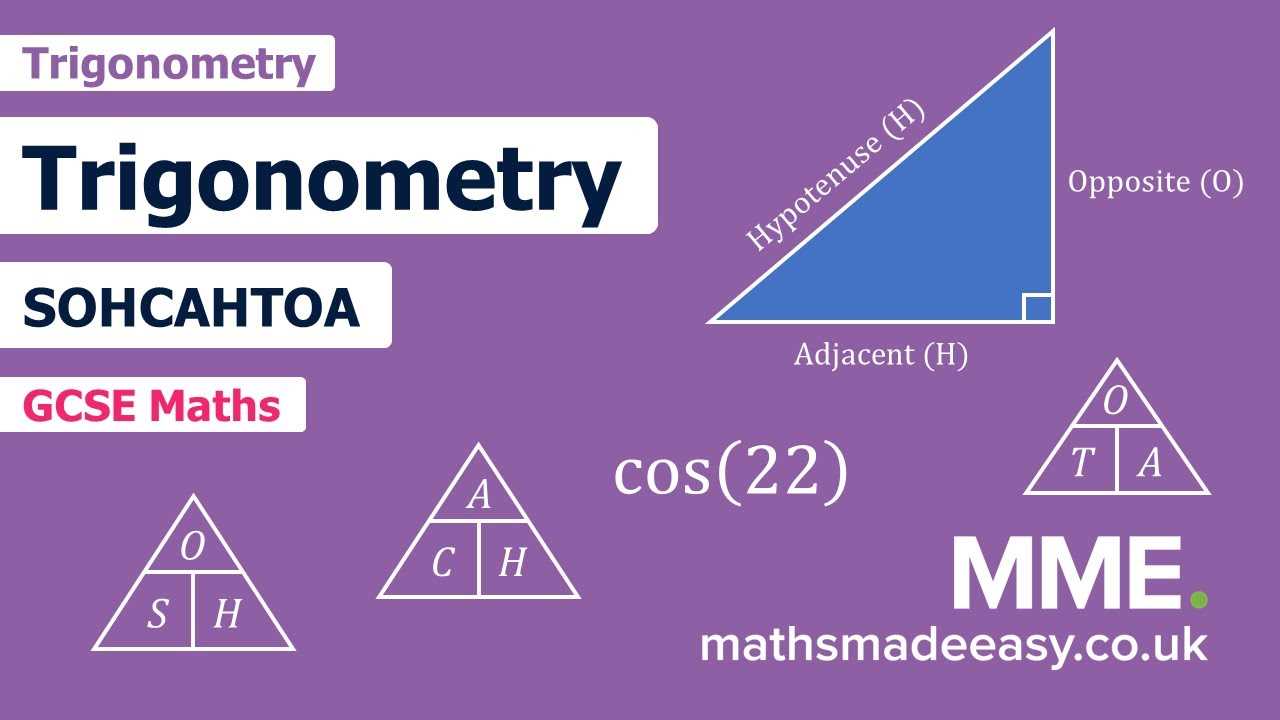
Understanding Basic Trigonometric Ratios
The relationships between the sides of a right triangle and its angles are central to many mathematical concepts. By learning the basic ratios, students can approach problems with greater clarity and precision. These ratios serve as the foundation for more advanced topics and help in solving real-world challenges involving angles and lengths.
There are three primary ratios that are essential to mastering this area of study:
- Sine (sin): The ratio of the opposite side to the hypotenuse.
- Cosine (cos): The ratio of the adjacent side to the hypotenuse.
- Tangent (tan): The ratio of the opposite side to the adjacent side.
Each of these ratios can be used to find unknown values in a triangle when given certain information, such as the measure of one angle or the length of one side. Understanding how these ratios work together allows for effective problem-solving across a wide range of scenarios.
For example, in a right triangle with an angle ?, the following relationships hold:
- sin(?) = opposite / hypotenuse
- cos(?) = adjacent / hypotenuse
- tan(?) = opposite / adjacent
These basic ratios are not only crucial for geometry, but they also lay the groundwork for more complex mathematical techniques used in fields like physics, engineering, and computer science. Mastery of these concepts opens up the path to solving more intricate problems with confidence.
How to Solve Right-Angle Triangles
Solving right-angle triangles is a fundamental skill in geometry and various applied fields. When dealing with such triangles, the goal is often to find unknown sides or angles based on the given information. With the right approach, these problems become straightforward by applying specific methods and principles that link the sides and angles of the triangle.
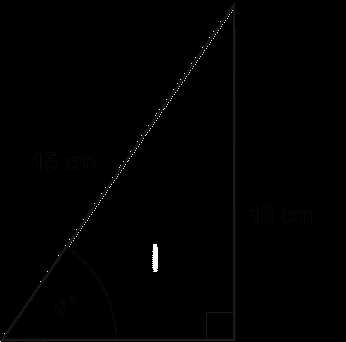
Using Pythagoras’ Theorem
One of the most powerful tools for solving right-angle triangles is Pythagoras’ theorem. This theorem states that for any right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The formula is:
c? = a? + b?
Where c is the hypotenuse, and a and b are the other two sides. This equation allows you to find an unknown side if the other two are known.
Using Basic Ratios
When one of the angles other than the right angle is known, the basic ratios (sine, cosine, tangent) can be applied to find the remaining unknowns. Here’s how:
- To find the opposite side, use: opposite = hypotenuse ? sin(?)
- To find the adjacent side, use: adjacent = hypotenuse ? cos(?)
- To find the opposite side using the adjacent side, use: opposite = adjacent ? tan(?)
These relationships allow you to solve for missing sides or angles as long as you have one angle or one side known. Remember, solving right-angle triangles relies heavily on understanding the interplay between the sides and angles, as well as applying the correct formulas.
Common Identities to Remember
In many mathematical problems, recognizing key relationships between different functions can significantly simplify the process of finding solutions. These fundamental identities are often the foundation for solving complex problems. By memorizing and understanding these identities, you can quickly manipulate expressions and make calculations easier.
Basic Pythagorean Identities
These identities are essential for simplifying expressions involving sine, cosine, and other functions. They are derived from the Pythagorean theorem and are frequently used to convert between functions or simplify equations.
- sin?(?) + cos?(?) = 1
- 1 + tan?(?) = sec?(?)
- 1 + cot?(?) = csc?(?)
Co-Function Identities
These identities show the relationship between the functions of complementary angles (angles that add up to 90°). Understanding them is helpful when working with angles that appear in pairs or require simplifications.
- sin(90° – ?) = cos(?)
- cos(90° – ?) = sin(?)
- tan(90° – ?) = cot(?)
- cot(90° – ?) = tan(?)
- sec(90° – ?) = csc(?)
- csc(90° – ?) = sec(?)
Memorizing these common identities not only helps simplify expressions but also improves efficiency when solving problems. With practice, you’ll be able to apply these identities seamlessly to find unknown values and solve more complex challenges.
Practical Applications of Trigonometry
The study of angles and their relationships is not only a theoretical pursuit but also a vital tool used in many real-world fields. From construction and navigation to physics and engineering, understanding how angles interact with distances and forces is crucial. By applying mathematical principles to practical situations, we can solve problems ranging from building structures to analyzing waves and forces.
One of the most common uses is in architecture and construction, where precise measurements are needed to ensure stability and safety. Whether it’s determining the height of a building, the slope of a roof, or the angle of a staircase, the ability to calculate angles and distances accurately is fundamental to the design and construction process.
In navigation, the ability to measure angles and distances helps to chart courses for ships, planes, and even satellites. Pilots, for instance, use angular measurements to calculate flight paths, while sailors rely on them to determine direction and distance over the seas. Similarly, in astronomy, astronomers use these principles to calculate the positions of celestial bodies and predict their movements.
Another key area where these concepts are applied is in physics, particularly when analyzing forces. When studying oscillations, waves, or the motion of objects, understanding the angle at which forces are applied allows for better predictions and solutions. This is essential for everything from engineering designs to understanding the behavior of light and sound waves.
Tips for Answering Trigonometric Problems

Approaching mathematical tasks involving angles and geometric relationships requires a structured strategy. With the right preparation and mindset, solving problems becomes much more manageable. The key is to stay organized, understand the concepts clearly, and apply them effectively to each situation.
Key Strategies for Success
- Understand the Problem: Carefully read each problem to identify the given information and what needs to be found. Highlight key numbers, angles, and relationships that can guide your solution process.
- Use Diagrams: Drawing a clear diagram of the situation can help visualize the problem, making it easier to apply formulas and identify missing values. Label all known and unknown variables.
- Know Your Identities: Familiarize yourself with the core mathematical relationships. Recognizing when to apply Pythagorean identities, co-function identities, or basic ratios can save valuable time during calculations.
- Choose the Right Formula: Based on the problem type, decide whether to use basic ratios (sine, cosine, tangent) or more advanced formulas like the law of sines or cosines. The correct choice can simplify the solution.
- Check Units: Ensure all measurements are in the same unit. Converting between radians and degrees is a common step that can prevent errors.
- Double-Check Calculations: After solving for an unknown, recheck the calculations. Small arithmetic mistakes can lead to incorrect results, so verifying each step helps avoid errors.
Time Management Tips
- Prioritize Simple Problems: Start with the questions that seem straightforward. Solving these first builds confidence and allows more time for difficult problems later.
- Don’t Get Stuck: If you encounter a particularly challenging problem, move on and return to it later. Spending too much time on one question can affect the rest of your performance.
- Practice Under Time Constraints: Practice solving problems within a set time limit to simulate the pressure of a real test. This will help you manage time more effectively during the actual task.
With consistent practice and a strategic approach, you can tackle even the most challenging tasks with confidence. Keep refining your skills, and remember that the more familiar you become with the concepts, the easier problem-solving becomes.
Identifying Key Information in Problems
When solving mathematical challenges involving angles and geometric shapes, it’s crucial to extract the most relevant details from the problem statement. The ability to identify key information quickly can significantly streamline the solution process. Often, problems present a mix of data, and determining what is essential helps to avoid unnecessary complexity and focus on what truly matters.
The first step is to carefully read the problem, paying close attention to the given values, relationships, and what needs to be found. Make sure to note all measurements such as side lengths, angles, and any additional instructions or constraints provided in the problem. These details guide the choice of formulas and techniques for solving the task.
Here are some tips to help identify important information:
- Look for Known Values: Identify all the given side lengths, angles, and any other relevant data. These are the starting points for applying mathematical principles.
- Note the Unknowns: Pay attention to what the problem is asking for–whether it’s an unknown side, angle, or a ratio between certain elements.
- Identify Key Relationships: Look for clues in the problem that suggest specific relationships between sides and angles. For example, if you’re dealing with a right triangle, recognize if Pythagorean theorem or sine/cosine ratios are applicable.
- Understand Any Special Conditions: Sometimes, problems come with special conditions such as angles being complementary or supplementary, or angles in different quadrants. These conditions can help direct the solution approach.
By focusing on these elements, you’ll quickly determine the most effective method for solving the problem. Identifying key information early on can save time and increase your chances of solving the problem correctly.
How to Use the Unit Circle
The unit circle is a powerful tool for understanding the relationships between angles and the values of basic functions. By using this circle, you can visualize the behavior of sine, cosine, and tangent for various angles, making it easier to solve a wide range of problems. The unit circle provides a geometric perspective that simplifies the calculation of function values for both familiar and less common angles.
To use the unit circle effectively, it’s important to understand its structure. The unit circle is a circle with a radius of one unit, centered at the origin of a coordinate plane. Each point on the circle corresponds to an angle, and the coordinates of that point represent the values of the cosine and sine of the angle.
Steps for Using the Unit Circle
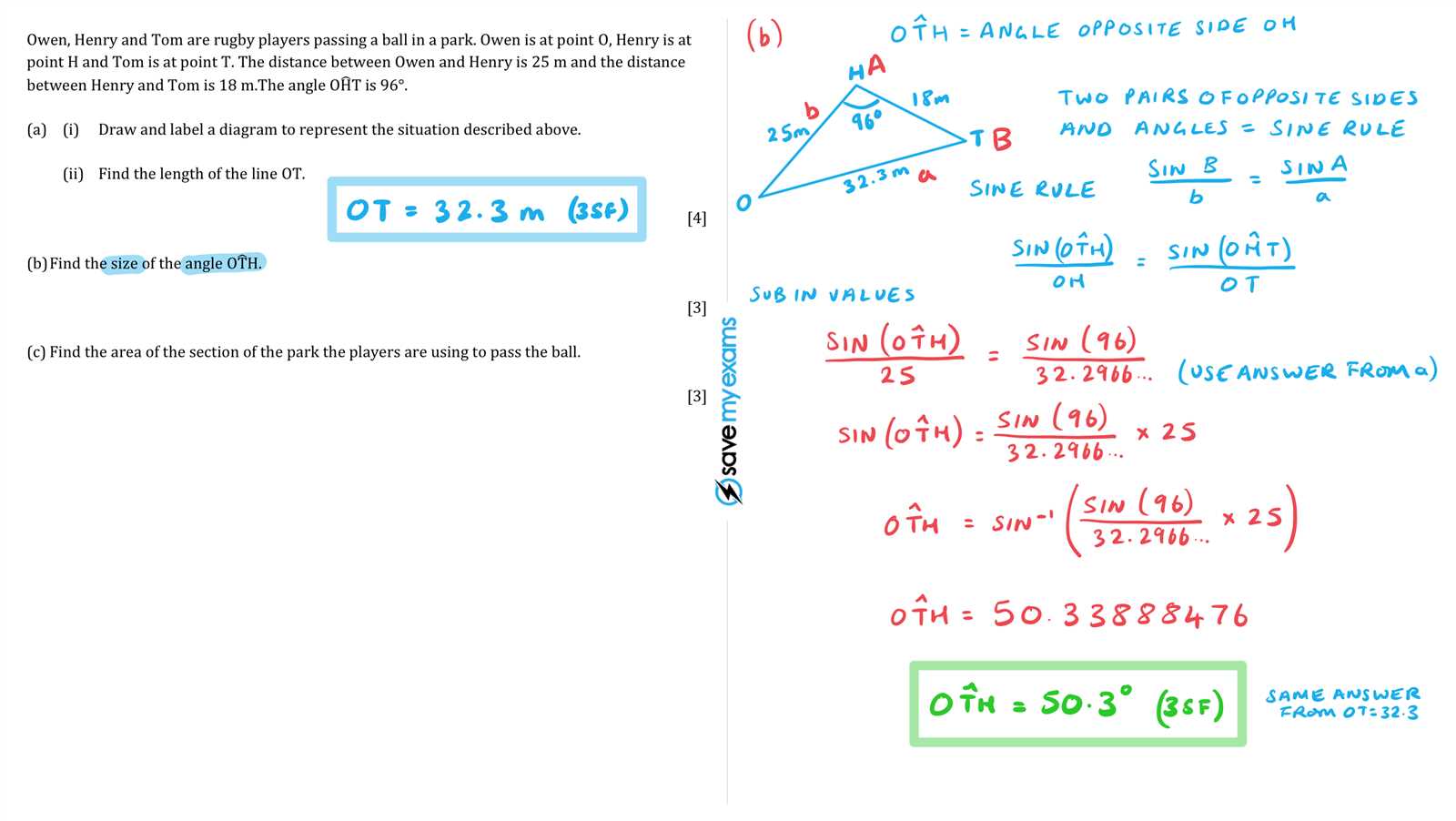
- Know the Key Angles: The most important angles to remember are 0°, 30°, 45°, 60°, 90°, and their corresponding values in radians (0, ?/6, ?/4, ?/3, ?/2). These angles appear frequently in problems.
- Understand the Coordinates: The coordinates of any point on the unit circle are (cos(?), sin(?)), where ? is the angle. For example, at 0°, the coordinates are (1, 0), meaning cos(0°) = 1 and sin(0°) = 0.
- Use Symmetry: The unit circle has symmetrical properties that make finding values easier. For instance, values of sine and cosine repeat in different quadrants, so memorizing the values for one quadrant can help deduce those for the others.
- Convert Between Radians and Degrees: Angles can be expressed in either radians or degrees. For example, 180° is equal to ? radians. Knowing these conversions helps to quickly identify angle measures on the unit circle.
- Apply the Functions: To find the sine or cosine of an angle, locate the corresponding point on the unit circle. The x-coordinate gives the cosine, and the y-coordinate gives the sine. For tangent, divide the sine by the cosine (tan(?) = sin(?) / cos(?)).
By practicing with the unit circle, you’ll become more comfortable identifying function values for different angles, simplifying calculations, and visualizing problems in a geometric context. This understanding will significantly enhance your ability to solve problems involving angles and circular motion.
Working with Angles in Different Units
Angles can be expressed in various units, the most common of which are degrees and radians. Understanding how to work with these different units is essential when solving problems involving angular measurement. Converting between units allows for flexibility and ensures that calculations are performed correctly, regardless of the unit being used. By mastering these conversions and understanding when each unit is appropriate, you can approach problems with confidence and accuracy.
Degrees and Radians: An Overview
Degrees are the most familiar unit for measuring angles, with a full circle consisting of 360°. Radians, however, are often preferred in more advanced mathematics and physics due to their direct relationship with the arc length of a circle. One radian is the angle subtended by an arc whose length is equal to the radius of the circle, and a full circle corresponds to 2? radians.
The key difference between degrees and radians lies in their relationship to the circle. Degrees divide the circle into 360 equal parts, while radians divide the circle based on the circumference. Understanding how to convert between these units is a crucial skill for solving a wide variety of angular problems.
Conversion Between Degrees and Radians
To convert between degrees and radians, the following formulas can be used:
| Conversion | Formula |
|---|---|
| Degrees to Radians | radians = degrees ? (? / 180) |
| Radians to Degrees | degrees = radians ? (180 / ?) |
For example, to convert 45° to radians, you would use the formula:
45 ? (? / 180) = ? / 4 radians
Similarly, to convert ?/3 radians to degrees, you would calculate:
? / 3 ? (180 / ?) = 60°
By practicing these conversions, you’ll become more comfortable working with both units and be able to switch between them as needed for various problems. Both degrees and radians are commonly used in different contexts, so knowing how to navigate between them will greatly enhance your problem-solving skills.
Trigonometric Equations and How to Solve Them
Mathematical problems involving angular relationships often require solving equations that contain trigonometric functions. These equations can seem complex at first, but with a systematic approach, they can be solved step by step. The key is recognizing the form of the equation, applying appropriate identities, and isolating the variable. Solving such equations is essential for finding unknown angles or side lengths in various real-world situations.
Steps for Solving Trigonometric Equations
When tackling an equation, it’s important to follow a clear set of steps to ensure accuracy and efficiency. Below are the general procedures that can help simplify the process:
- Step 1: Identify the function: Look at the given equation and determine which trigonometric function (sine, cosine, tangent, etc.) is involved. This will help you decide which strategies to apply.
- Step 2: Isolate the trigonometric function: If the equation involves more than one term, try to rearrange it so that the trigonometric function is by itself on one side of the equation.
- Step 3: Apply trigonometric identities: Use any relevant identities (such as Pythagorean, co-function, or double-angle identities) to simplify the equation further.
- Step 4: Solve for the angle: Once the trigonometric function is isolated, find the angle by taking the inverse of the function. This may involve using a calculator or recognizing special angles.
- Step 5: Check for multiple solutions: Depending on the domain of the problem, there may be more than one solution. Be sure to account for all possible values of the angle that satisfy the equation.
Example Problem
Consider the equation: sin(x) = 0.5.
- Step 1: Identify the function: We are dealing with the sine function.
- Step 2: Isolate the function: The sine function is already isolated on one side of the equation.
- Step 3: Apply identities: No additional identities are needed in this case.
- Step 4: Solve for the angle: Using the inverse sine function, x = sin??(0.5) = 30° or 150° (since sine is positive in both the first and second quadrants).
- Step 5: Check for other solutions: The solutions within the range 0° to 360° are x = 30° and x = 150°.
By following these steps and practicing with different types of equations, you can develop a solid understanding of how to solve problems involving angular relationships. With experience, solving these equations becomes quicker and more intuitive.
Graphing Sine, Cosine, and Tangent Functions
Graphing functions involving angles allows for a clear understanding of their periodic behavior and how they relate to each other. The sine, cosine, and tangent functions each have distinct shapes, but all exhibit repeating patterns known as periodicity. Understanding how to graph these functions provides insight into their behavior over different intervals, helping to solve a variety of problems related to oscillations, waves, and rotations.
Graphing the Sine and Cosine Functions
The sine and cosine functions are closely related, both having a periodic pattern with a period of 360° or 2? radians. The main difference is in their starting points: the sine function starts at 0, while the cosine function starts at its maximum value. These functions are often used to model oscillations and waves, making their graphical representation important in many fields.
- Sine Function: The sine curve begins at the origin (0,0) and moves upward toward 1, then downward to -1, completing one full cycle over 360° or 2? radians. It has the general form of y = sin(x).
- Cosine Function: The cosine curve begins at its maximum value of 1 at 0°, then decreases to -1 at 180° and returns to 1 at 360°. The equation for the cosine function is y = cos(x).
Graphing the Tangent Function
The tangent function behaves differently from sine and cosine. It has a periodicity of 180° or ? radians, and it’s known for its asymptotes, which occur at values where the cosine function equals zero (since tangent is the ratio of sine to cosine). The graph of the tangent function starts at 0, rises steeply, and has vertical asymptotes where the function is undefined.
- Tangent Function: The graph of the tangent function begins at the origin (0,0), rises rapidly, and approaches vertical asymptotes at ±90° (±?/2 radians), 180° (? radians), and so on. Its general form is y = tan(x).
When graphing these functions, it is crucial to understand their key features, such as amplitude, period, and phase shifts, which can be adjusted by modifying the function’s equation. Practicing with these graphs allows for a deeper understanding of their periodic nature and is helpful in solving many real-world problems.
Inverse Trigonometric Functions Explained
Inverse functions are crucial tools for determining unknown angles when given the values of trigonometric ratios. While standard trigonometric functions take an angle as input and return a ratio, their inverses work in the opposite way, returning an angle when given a ratio. Understanding these inverse functions is essential for solving problems involving angle determination from known ratios, especially when working with right triangles or circular motion.
Understanding Inverse Functions

The inverse of a trigonometric function “reverses” the operation of the original function. For example, while the sine function takes an angle and returns a ratio, its inverse (known as arcsine) takes a ratio and returns the angle. This inverse relationship allows us to solve for angles when only the ratios of the sides of a triangle are known.
- Inverse Sine (arcsin): Given a ratio (such as the opposite side divided by the hypotenuse), the inverse sine function returns the corresponding angle.
- Inverse Cosine (arccos): This function returns the angle when given the ratio of the adjacent side to the hypotenuse.
- Inverse Tangent (arctan): The inverse tangent function provides the angle based on the ratio of the opposite side to the adjacent side.
Key Values for Inverse Functions
When using inverse trigonometric functions, it’s important to remember that the results will always fall within specific ranges. These ranges ensure the functions return a unique angle for every possible ratio.
| Function | Range |
|---|---|
| arcsin(x) | -90° to 90° (-?/2 to ?/2 radians) |
| arccos(x) | 0° to 180° (0 to ? radians) |
| arctan(x) | -90° to 90° (-?/2 to ?/2 radians) |
These ranges are important because they restrict the values returned by the inverse functions to a single angle. This ensures that the inverse functions are well-defined, meaning there’s only one solution for each ratio.
Inverse functions are invaluable when solving real-world problems where the angle is unknown, but the trigonometric ratio is given. By applying these functions correctly, you can determine the precise angle in a variety of situations, from navigation and engineering to physics and architecture.
Special Triangles in Trigonometry
Certain types of triangles are fundamental when working with angular relationships, especially when solving for sides or angles. These special triangles, often encountered in geometry and physics, have unique properties that make them easier to work with. Understanding these triangles can simplify calculations and lead to quick solutions without requiring the use of complex formulas.
45°-45°-90° Triangle
One of the most important special triangles is the 45°-45°-90° triangle, which is an isosceles right triangle. In this triangle, the two legs are congruent, and the angles opposite these legs are both 45°. The hypotenuse is always v2 times the length of one leg. This property makes it simple to calculate the sides when one leg is known.
- Properties: The legs are equal in length, and the ratio of the hypotenuse to the leg is v2:1.
- Example: If the length of each leg is 1, then the length of the hypotenuse is v2.
30°-60°-90° Triangle
The 30°-60°-90° triangle is another important special triangle. It is a right triangle with angles of 30°, 60°, and 90°. In this triangle, the ratio of the sides is fixed: the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is v3 times the length of the shorter leg.
- Properties: The side opposite the 30° angle is half the length of the hypotenuse, while the side opposite the 60° angle is v3 times the shorter leg.
- Example: If the shortest leg is 1, then the hypotenuse is 2, and the longer leg is v3.
These special triangles provide a straightforward method for solving many problems involving angles and side lengths. Recognizing these triangles and understanding their properties is essential for anyone working with angular relationships, as they simplify the process and reduce the need for complex calculations.
Common Mistakes in Trigonometry Exams
When solving problems involving angles and ratios, students often make certain errors that can lead to incorrect results. These mistakes can stem from misunderstandings of key concepts, careless miscalculations, or failure to apply proper formulas. Recognizing these common pitfalls is essential for improving performance and avoiding frustration during problem-solving.
One frequent error is confusing the sine, cosine, and tangent functions, especially when switching between different formulas. Another mistake involves overlooking the domain and range of inverse functions, which can lead to incorrect angle values. Misapplying identities is also common, particularly when simplifying expressions or solving equations. Additionally, not paying attention to angle units–radians versus degrees–can result in incorrect answers. Finally, when working with special triangles, neglecting their inherent ratios can lead to incorrect side length calculations.
To minimize these mistakes, it’s important to thoroughly review the concepts and practice a wide range of problems. Familiarizing oneself with the properties of functions and identities can provide a solid foundation, and paying close attention to each step can help reduce careless errors. Taking the time to check work and review answers is a helpful strategy for catching mistakes before finalizing solutions.
How to Manage Time During the Exam
Effective time management is crucial when tackling complex problems under pressure. Without a proper strategy, it’s easy to become overwhelmed and fall behind on tasks, leading to incomplete answers and unnecessary stress. Managing time wisely allows for more thoughtful responses and ensures every part of the test is addressed.
One of the best strategies is to allocate a specific amount of time for each section of the test. This way, you can avoid spending too much time on a single problem, leaving enough time to address all questions. Start by quickly scanning the entire test, identifying easier problems that can be solved quickly. Starting with these helps build confidence and allows for more time on difficult tasks later.
Prioritize tasks based on difficulty and point value. If you encounter a particularly challenging problem, move on and return to it later if time permits. This prevents spending excessive time on one issue while potentially missing out on simpler questions. It’s also helpful to keep an eye on the clock and regularly check your progress, adjusting your pace as needed to stay on track.
Finally, avoid the temptation to overthink problems. Trust in your preparation and focus on applying the concepts you’ve studied. Taking brief mental breaks, if allowed, can also help to refresh your mind and maintain focus during longer tests.
Resources for Practice and Review
When preparing for assessments or deepening your understanding of angular relationships, having access to the right resources is crucial. A variety of tools and materials can help reinforce concepts, clarify doubts, and provide ample opportunities for hands-on practice. Whether you’re a beginner or looking to refine advanced techniques, these resources can support your learning journey.
There are several platforms available to practice solving problems and reviewing key concepts. Online tutorials, interactive problem sets, and textbooks can provide structured learning, while video lessons offer step-by-step explanations of challenging topics. Additionally, practice worksheets and online quizzes can help reinforce understanding and provide immediate feedback.
Types of Resources
| Resource Type | Benefits |
|---|---|
| Interactive Websites | Engage with problem-solving tools and receive instant feedback on solutions. |
| Textbooks | Offer detailed explanations, examples, and practice problems with solutions. |
| Video Tutorials | Provide visual explanations and demonstrations for various concepts. |
| Online Quizzes | Test your knowledge in real-time, with immediate feedback and explanations. |
| Practice Worksheets | Help you practice specific types of problems and improve problem-solving speed. |
By regularly using these resources, you can reinforce your understanding, practice essential skills, and build the confidence needed to perform well in assessments. Whether you prefer structured learning, hands-on practice, or visual aids, there is a wealth of materials available to support your review process.
Where to Find Practice Problems
Finding high-quality practice problems is key to improving your skills and mastering concepts related to angles and their relationships. The more problems you work through, the more comfortable you will become with the material. There are numerous places where you can access a wide range of problems, each tailored to different levels of difficulty and areas of focus.
- Online Educational Platforms – Websites like Khan Academy, Coursera, and edX offer a variety of practice exercises, complete with step-by-step explanations and solutions.
- Textbooks – Most textbooks provide exercises at the end of each chapter, covering basic to advanced problems with detailed solutions.
- Educational Apps – Mobile apps like Photomath and Wolfram Alpha allow users to solve problems and get instant feedback, making them a great option for on-the-go practice.
- University Websites – Many university websites provide access to past assignments and practice tests, which can be useful for preparing for similar topics.
- Online Forums – Platforms like Reddit, Stack Exchange, and various online communities host forums where users can share problems, discuss solutions, and work together to improve their skills.
- Interactive Problem Solving Tools – Websites such as Brilliant.org and Art of Problem Solving offer interactive problem-solving challenges, designed to stimulate thinking and reinforce concepts.
By using these resources, you can ensure that you are exposed to a broad variety of problems, covering all aspects of the material. Practice not only strengthens your understanding but also helps develop faster problem-solving skills, which are crucial for assessments and real-world applications.