
As you approach the final stages of your mathematical studies, it’s essential to consolidate your understanding of key concepts and strengthen your problem-solving skills. This guide is designed to help you focus on the areas that are most crucial for achieving success. With a systematic approach, you can confidently tackle any challenge that may arise during the evaluation process.
Familiarity with the underlying principles, as well as practice with a variety of problems, will enhance your ability to perform under pressure. Mastering the fundamentals and refining your techniques will make all the difference, whether you’re working with shapes, calculations, or abstract theories.
Throughout this guide, you’ll find tips, tricks, and practical advice to make your preparation more efficient and effective. By focusing on the most important topics and practicing diligently, you’ll be well-equipped to showcase your skills and knowledge when it matters most.
Mathematics Concepts Final Preparation
As the time approaches for your final assessment in the field of mathematics, it’s important to focus on the core principles and sharpen your problem-solving abilities. This section will guide you through the essential topics that will help ensure your success and build your confidence for the upcoming challenges. By reviewing key areas and practicing regularly, you’ll be well-prepared for any task presented during the evaluation.
Critical Concepts to Focus On
Key mathematical theories and formulas are central to solving problems quickly and accurately. Understanding the fundamental rules and their applications in various scenarios is crucial. Whether it’s working with angles, areas, or understanding complex relationships between shapes, strengthening your knowledge in these areas will allow you to navigate through any related problems efficiently.
Effective Problem-Solving Strategies

When preparing for the final stage, practicing a variety of problem types is essential. Develop strategies for approaching both simple and complex problems, ensuring that you can solve them step by step. Breaking down each task into smaller parts and applying logical reasoning will allow you to tackle even the most difficult challenges with ease.
Key Concepts to Master for Mathematics
To excel in the final stage of your mathematical studies, it is crucial to understand the foundational ideas that underpin the subject. Mastering these core principles will not only help you solve problems with greater ease but will also deepen your understanding of how various elements are interconnected. Focusing on these essential topics will provide a solid base for tackling more complex challenges.
Strengthening your knowledge in areas such as spatial relationships, measurement, and calculation methods is vital. Whether you are working with shapes, angles, or equations, each concept plays a significant role in solving tasks efficiently and accurately. With practice and focus, these key ideas will become second nature, giving you the confidence to approach any question with a clear strategy.
Essential Mathematical Formulas to Remember
When preparing for any assessment in this field, having a strong grasp of fundamental equations is crucial. These formulas serve as tools to solve a wide range of problems and should be memorized to ensure quick and accurate results. Whether you’re calculating areas, volumes, or relationships between various shapes, these core formulas will provide the foundation needed to tackle different challenges effectively.
Key equations, such as those for calculating the area of different shapes, the circumference of circles, and the Pythagorean theorem, are indispensable in solving many types of problems. Understanding when and how to apply each formula will enhance your ability to navigate complex tasks and ensure you’re well-prepared for any challenge that comes your way.
How to Approach Proofs in Mathematics
Solving proofs can seem challenging, but with a structured approach, they become more manageable. The key is to break down the problem into smaller steps, using logical reasoning and known principles to connect each part. A proof is essentially a way of demonstrating that something is true based on established facts, so understanding the connections between concepts is vital for success.
Steps to Tackle a Proof
When facing a proof, follow these general steps to ensure clarity and accuracy:
- Understand the Given Information: Carefully read through the problem and identify the given conditions.
- Identify What Needs to Be Proven: Clearly define the statement or property you are trying to prove.
- Choose Relevant Theorems: Select theorems or properties that relate to the problem and will help you build the proof.
- Work Step-by-Step: Use logical reasoning to connect each step, ensuring every conclusion is based on the previous one.
- Write Clearly: Present your argument in a clear, organized manner, showing all steps and justifications.
Common Proof Techniques

There are several techniques you can use to approach different types of proofs:
- Direct Proof: Start from the known facts and build your argument step by step until you reach the conclusion.
- Proof by Contradiction: Assume the opposite of what you need to prove, and show that it leads to a contradiction.
- Inductive Proof: Prove the statement for a base case, then prove it holds for the next case, continuing this pattern.
- Proof by Contrapositive: Prove the contrapositive of the statement instead, which is logically equivalent to proving the original statement.
Understanding Geometric Shapes and Properties
To succeed in mathematical assessments, it’s essential to have a deep understanding of different shapes and their characteristics. Recognizing how these forms behave and interact within various contexts allows you to solve complex problems efficiently. From simple polygons to more intricate figures, each shape has its unique properties that can be applied to a variety of tasks.
Familiarity with key shapes such as triangles, quadrilaterals, and circles is fundamental. Understanding the specific properties of each–like symmetry, angles, and side lengths–helps in determining relationships and solving related problems. Mastering these concepts provides a foundation for tackling more advanced topics and challenges.
Additionally, it’s important to understand how to manipulate these shapes, such as calculating areas, perimeters, and volumes, and recognizing their roles in more complex theorems. Each property plays a significant part in developing a clearer, more comprehensive understanding of spatial relationships.
Tips for Solving Word Problems in Mathematics
Word problems often present mathematical challenges in a real-world context, requiring both logical reasoning and the ability to translate the narrative into mathematical expressions. To solve these problems effectively, it’s important to approach them systematically, breaking down the information step by step. Following a clear strategy will help you identify the key elements and determine the best method for finding the solution.
Steps for Solving Word Problems
Here are some key steps to guide you through solving word problems:
- Read the Problem Carefully: Make sure you understand all the given information and what is being asked before proceeding.
- Identify Known and Unknown Values: Highlight the information provided and note what you need to find.
- Translate Words into Equations: Convert the verbal description into mathematical expressions or equations that represent the problem.
- Choose the Right Formula: Select the appropriate mathematical formula or method based on the information you’ve identified.
- Solve Step by Step: Work through the equation or formula, performing each step carefully to avoid mistakes.
- Check Your Work: After finding a solution, review each step and verify that the answer makes sense within the context of the problem.
Additional Tips for Success
When facing complex word problems, consider these helpful tips:
- Draw a Diagram: Visualizing the problem can help you better understand the relationships between the elements involved.
- Break Down Large Problems: If the problem feels overwhelming, break it into smaller, more manageable parts.
- Look for Key Words: Certain words often indicate specific operations, such as “sum,” “difference,” or “product,” which can guide your calculations.
- Practice Regularly: The more problems you solve, the better you’ll become at recognizing patterns and applying the correct methods quickly.
Common Mistakes to Avoid in Mathematics
While solving mathematical problems, certain errors can easily creep in, especially when dealing with complex tasks. Recognizing and avoiding these common pitfalls will not only help you improve your accuracy but also increase your overall efficiency. Whether it’s a small misstep in calculations or overlooking key concepts, being aware of frequent mistakes can save you valuable time and ensure more reliable results.
Key Mistakes to Watch Out For

Here are some of the most common mistakes students make, along with tips on how to avoid them:
| Common Mistake | How to Avoid It |
|---|---|
| Forgetting to label key elements (like sides or angles) | Always label every part of the diagram clearly and double-check your labels during each step. |
| Misapplying formulas or theorems | Ensure you understand when and how to use each formula or theorem. Review your formulas regularly. |
| Not simplifying the final answer | Always simplify your results, especially when dealing with fractions or square roots. |
| Skipping steps or rushing through problems | Take your time and work through problems methodically. It’s better to be thorough than to rush and make errors. |
| Overlooking units of measurement | Always check that your units are consistent throughout the problem and include them in your final answer. |
By paying attention to these common errors and following the tips to avoid them, you’ll be in a better position to perform accurately and effectively in mathematical tasks.
Reviewing Coordinate Geometry Techniques
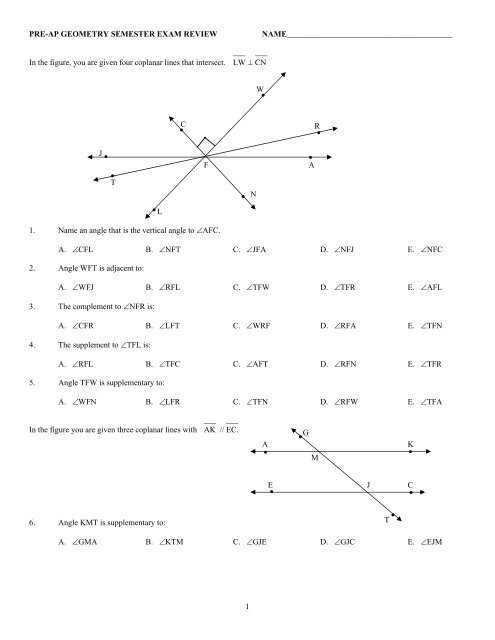
Understanding the relationship between algebra and spatial concepts is a crucial aspect of solving problems in this field. The key to mastering tasks involving points, lines, and distances is familiarity with essential methods that allow you to manipulate and analyze coordinates effectively. These techniques enable you to solve a variety of challenges, from finding the slope of a line to determining the distance between two points.
Important Techniques to Master
Here are the fundamental methods and formulas you should be familiar with:
- Distance Formula: This formula helps calculate the straight-line distance between two points, given their coordinates:
- d = √((x₂ – x₁)² + (y₂ – y₁)²)
- Slope Formula: The slope of a line is calculated using the difference in the y-values divided by the difference in the x-values:
- m = (y₂ – y₁) / (x₂ – x₁)
- Midpoint Formula: To find the midpoint between two points, average their x and y coordinates:
- Midpoint = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)
Practical Applications
These formulas play a crucial role in various problem-solving scenarios. By applying the distance formula, for example, you can determine how far apart two locations are, which is useful in navigation problems. The slope formula allows you to determine the steepness of a line, which can be applied in real-world contexts such as construction and design. Lastly, the midpoint formula is useful for finding the center point between two locations, aiding in tasks such as bisecting a segment.
Important Theorems for Mathematics Assessments
Mastering key theorems is essential for solving complex problems effectively. These fundamental concepts provide the foundation for understanding relationships between various shapes and their properties. By knowing when and how to apply these theorems, you can quickly find solutions and simplify seemingly difficult tasks. Below are some of the most important theorems you should be familiar with, which will greatly aid in your problem-solving process.
Key Theorems to Know
The following theorems are essential for solving a wide range of problems:
| Theorem | Description |
|---|---|
| Pythagorean Theorem | This theorem relates the sides of a right triangle: a² + b² = c², where c is the hypotenuse. |
| Triangle Sum Theorem | The sum of the interior angles of any triangle is always 180°. |
| Parallel Postulate | If a line is parallel to another, corresponding angles are equal when a transversal intersects them. |
| Angle Bisector Theorem | The angle bisector of an angle in a triangle divides the opposite side in proportion to the adjacent sides. |
| Congruence Theorems | These include SSS, SAS, ASA, and AAS, which help determine when two triangles are congruent. |
Understanding and applying these theorems will allow you to solve a variety of tasks efficiently and accurately. Whether calculating side lengths, angles, or area, these fundamental principles are indispensable for success in problem-solving scenarios.
Time Management Strategies for Mathematics Assessments
Efficiently managing your time during assessments is crucial for maximizing your performance. Proper preparation and planning allow you to complete tasks accurately within the given time frame. By organizing your approach and prioritizing questions, you can ensure that you allocate enough time to each section while avoiding unnecessary stress. The following strategies will help you optimize your time and approach each question with confidence.
Effective Time Management Tips
Here are some proven strategies to help you manage your time effectively during a mathematics assessment:
- Familiarize Yourself with the Format: Understand the structure of the assessment beforehand, so you know how many sections or questions to expect and how much time to allocate to each.
- Start with Easier Questions: Begin by answering the questions you find easiest. This will build confidence and save time for more challenging problems later.
- Use a Timer: Set a timer for each section or individual question to avoid spending too much time on any one problem. This helps keep track of time and ensures you don’t rush at the end.
- Prioritize Your Strongest Areas: Focus on sections or questions that align with your strengths. This ensures you complete them accurately and on time.
- Leave Difficult Questions for Later: If a question feels too time-consuming, skip it initially and come back to it later if time permits.
Reviewing Your Work
- Allocate Time for a Final Review: Always leave some time at the end of the assessment to review your answers. This helps catch any mistakes and ensures accuracy.
- Double-Check Critical Calculations: Focus on reviewing questions that require precise calculations, ensuring all formulas and steps are correctly applied.
By implementing these strategies, you can approach your assessment with a clear plan, manage your time efficiently, and ensure that you complete every task to the best of your ability.
Mathematics Practice Problems to Solve

Practicing various problems is one of the most effective ways to prepare for assessments. By solving a wide range of challenges, you can develop a deeper understanding of the concepts and improve your problem-solving skills. Below are some essential practice problems to help reinforce key ideas and techniques that are commonly tested. Regularly working through these types of problems will enhance your ability to approach any task with confidence.
Practice Problems to Try
The following set of problems covers different aspects of mathematics and will help sharpen your skills:
| Problem | Description |
|---|---|
| Problem 1: Triangle Area | Find the area of a triangle with base 10 units and height 5 units. |
| Problem 2: Distance Between Points | Calculate the distance between the points (2, 3) and (5, 7). |
| Problem 3: Line Slope | Determine the slope of the line passing through the points (1, 2) and (4, 6). |
| Problem 4: Angle Measurement | Find the measure of the angle between two intersecting lines, given their slopes. |
| Problem 5: Pythagorean Theorem | Use the Pythagorean theorem to find the length of the hypotenuse in a right triangle with legs of 6 and 8 units. |
Regularly practicing these problems will not only increase your speed but also help you recognize patterns and identify the best strategies to use when tackling similar challenges in an assessment.
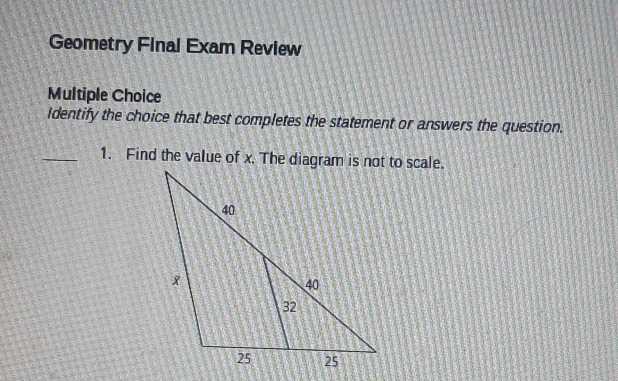
How to Tackle Diagrams Efficiently
Diagrams are often an essential part of problem-solving, helping to visualize relationships and key elements within a given scenario. Approaching them with the right mindset and techniques can significantly improve your ability to interpret and solve problems accurately. By focusing on the details of the diagram and applying appropriate methods, you can efficiently extract the necessary information and proceed with the solution.
Steps to Analyze Diagrams
Here are some effective steps to follow when working with diagrams:
- Label Key Elements: Start by labeling all known points, lines, and angles in the diagram. This helps to keep track of important information and ensures clarity as you proceed.
- Identify Known Relationships: Look for any geometric properties or relationships, such as parallel lines, perpendicular lines, symmetry, or congruence, which may assist in solving the problem.
- Highlight Important Sections: Use different colors or symbols to highlight critical areas such as angles, lengths, or intersections. This will help you quickly identify what needs to be calculated or proven.
- Draw Additional Lines: If necessary, draw auxiliary lines or shapes that might simplify the problem, such as altitudes, medians, or perpendicular bisectors.
Common Pitfalls to Avoid
- Overlooking Information: Make sure not to skip any given data in the diagram, even seemingly minor details could be critical.
- Relying Too Heavily on the Diagram: While diagrams are helpful, always check that the information you’ve drawn matches the conditions outlined in the problem.
- Misinterpreting Angles or Lengths: Double-check your angle and length measurements to avoid miscalculations that can lead to incorrect results.
By following these steps and being mindful of common mistakes, you can approach diagrams with confidence and efficiency, helping you solve problems with greater accuracy.
Using Graphing Tools in Assessments
Graphing tools are invaluable assets when it comes to solving complex problems that involve visualizing relationships between points, lines, and shapes. Mastering these tools can make it easier to interpret and analyze data, saving time and improving accuracy during a test. Knowing when and how to use graphing devices effectively can significantly enhance problem-solving efficiency, especially when dealing with coordinate-based challenges or visualizing spatial concepts.
When to Use Graphing Tools
Graphing tools should be employed strategically during problem-solving tasks. Consider using them in the following scenarios:
- When working with coordinates: Graphing points and lines on a coordinate plane can help visualize relationships and find distances or slopes more easily.
- For geometric shapes: When tasked with finding areas, perimeters, or angles in figures, graphing can provide a clear understanding of the problem’s layout and dimensions.
- To check the validity of results: Sometimes, graphing helps in verifying theoretical answers by providing a visual confirmation of your calculations.
Tips for Effective Use of Graphing Tools
- Label key points: Clearly mark all the relevant points and lines on the graph to avoid confusion.
- Use graphing scale consistently: Make sure to maintain a consistent scale to ensure accurate measurements and comparisons.
- Leverage gridlines for precision: Gridlines on graphing tools can assist in determining exact coordinates, angles, and distances.
- Use software or calculators when allowed: Many tools offer advanced functions like plotting multiple equations or calculating geometric properties, which can save time during tests.
With practice, using graphing tools efficiently will become second nature, helping you tackle problems with greater clarity and precision during your assessments.
How to Study Effectively
Studying for subjects that require a solid understanding of spatial relationships, measurements, and logical reasoning demands a structured and thoughtful approach. It’s not just about memorizing formulas but about building a deeper understanding of concepts, practicing regularly, and learning how to apply knowledge to solve various types of problems. Effective study strategies can help reinforce these principles and make problem-solving more intuitive.
The key to mastering this subject is consistency. Allocate time for regular practice, review your mistakes, and make sure you fully grasp the reasoning behind each solution. Active engagement, rather than passive reading, will lead to better retention and understanding.
Additionally, utilizing various resources like textbooks, online tutorials, and interactive problem sets can provide different perspectives on the material. Surrounding yourself with various methods can lead to breakthroughs in areas where you might be struggling.
Key Vocabulary for Your Assessment
Mastering the terminology used in subjects that focus on shapes, sizes, angles, and spatial relationships is crucial for success. Understanding the definitions of key terms enables you to recognize problem types, formulate strategies, and communicate solutions clearly. A strong grasp of relevant vocabulary not only improves comprehension but also ensures that you can interpret and solve problems more efficiently.
Make sure to familiarize yourself with terms related to lines, angles, figures, and transformations, as these will frequently appear in problems. Recognizing these terms and their properties will help you navigate questions with confidence.
What to Do on Assessment Day for Success
Success on test day involves more than just knowledge; it requires the right mindset, preparation, and approach. To perform at your best, it’s essential to manage both your mental and physical state. A calm, focused attitude paired with solid time management can significantly enhance your performance.
Start the day with a healthy breakfast to fuel your brain, and make sure to arrive early to avoid unnecessary stress. Bring all necessary materials, such as pens, calculators, or any other tools you may need. Take a few deep breaths before starting to help calm your nerves and clear your mind. Read through each question carefully and pace yourself throughout the test, ensuring you don’t rush through any sections.