Integrated Math 1 Semester 2 Final Exam Review Answers

Preparing for the end-of-term assessments in mathematics requires a solid understanding of key principles and problem-solving techniques. Whether you’re reviewing basic algebraic operations, mastering geometric concepts, or tackling complex equations, a structured approach can make all the difference in achieving your desired results.

Focus on essential topics that frequently appear in assessments, ensuring that you’re not only familiar with formulas but also comfortable applying them in various contexts. Each section builds upon prior knowledge, and strengthening your grasp of foundational skills will empower you to confidently tackle more advanced challenges.

To succeed, it is crucial to practice regularly, revisit difficult concepts, and develop strategies for identifying and correcting mistakes. By focusing on critical areas and utilizing available resources, you can approach the assessment with confidence and clarity.

Comprehensive Guide to Math 1 Exam

Achieving success in your upcoming test requires a clear understanding of key topics and consistent practice. This guide provides a structured approach to help you focus on the most important concepts, ensuring you’re prepared to solve problems with confidence. By breaking down the material into manageable sections, you’ll be able to tackle even the most complex problems more effectively.

Key Concepts to Focus On

To excel, it’s essential to focus on the core areas that frequently appear in assessments. These include algebraic manipulations, geometry basics, and functions. Mastery of these topics will not only prepare you for a wide range of questions but will also strengthen your problem-solving abilities. It’s important to practice both basic and advanced problems within each category to solidify your understanding.

Effective Problem-Solving Strategies

Developing a systematic approach to tackling problems is crucial. Break down each question into smaller, more manageable steps. Identify known values, recognize patterns, and carefully apply the correct methods to find the solution. Regular practice with timed drills can help you refine these skills and improve your efficiency under exam conditions.

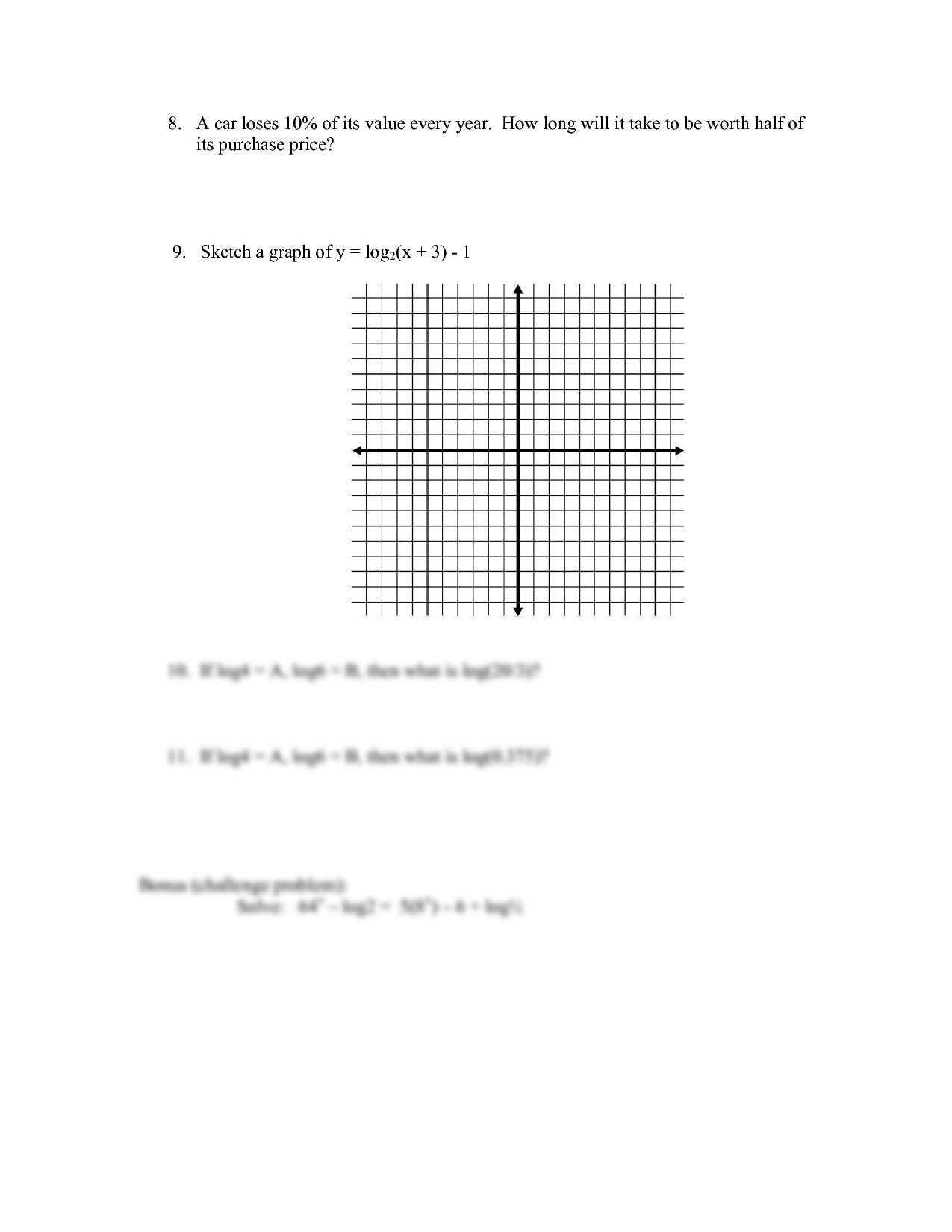
Key Topics for Semester 2 Review

To achieve success in your upcoming assessment, it’s essential to focus on the main concepts that will appear frequently. Understanding and mastering these key areas will allow you to approach the problems with confidence. Below is a list of critical topics to prioritize during your preparation, each representing a fundamental building block in the course material.

Topic	Description
Linear Equations	Understand how to solve equations involving variables on both sides, and work with different methods such as substitution and elimination.
Functions	Focus on understanding how to represent, analyze, and interpret different types of functions, including linear and quadratic functions.
Systems of Equations	Learn how to solve systems of equations using various methods like graphing, substitution, and elimination.
Polynomials	Review polynomial operations, including addition, subtraction, multiplication, and factoring techniques.
Quadratic Equations	Familiarize yourself with solving quadratic equations using factoring, completing the square, and the quadratic formula.
Inequalities	Work on solving and graphing linear and quadratic inequalities, including compound inequalities.

Understanding Core Mathematical Concepts

Mastering fundamental concepts is the key to succeeding in any mathematical assessment. By building a solid foundation, you ensure that you can solve a wide variety of problems with confidence. The core principles covered throughout the course form the basis for more advanced topics and are essential for problem-solving. This section will highlight the essential ideas you need to focus on to strengthen your understanding.

Concept	Description
Linear Equations	Learn how to manipulate equations involving variables, solve for unknowns, and understand the relationships between different types of linear expressions.
Functions and Relations	Understand the concept of functions as mappings between inputs and outputs, and practice identifying domain, range, and function types like linear and quadratic.
Systems of Equations	Explore methods to solve multiple equations simultaneously, focusing on both graphical and algebraic approaches like substitution and elimination.
Polynomials and Operations	Familiarize yourself with polynomial expressions, and practice performing operations such as addition, subtraction, multiplication, and factoring.
Inequalities	Study how to solve and graph inequalities, including linear and quadratic forms, and how to apply them to real-world problems.

Solving Linear Equations Effectively

Solving equations that involve variables on both sides is a fundamental skill that will appear in many types of problems. To handle these equations efficiently, it’s crucial to have a solid approach and clear understanding of the techniques involved. By applying systematic steps, you can reduce complexity and solve for the unknown with ease.

Steps to Solve Linear Equations

Follow these steps to effectively solve linear equations:

1. Isolate the variable on one side by using addition or subtraction.
2. Simplify both sides of the equation whenever possible.
3. Use multiplication or division to eliminate any coefficients that are attached to the variable.
4. Check your solution by substituting it back into the original equation.

Common Mistakes to Avoid

• Forgetting to apply the same operation on both sides of the equation.
• Mixing up the signs during simplification.
• Failing to check the solution after solving the equation.

With consistent practice and attention to detail, you will become proficient in solving these types of equations and develop a more intuitive understanding of their structure.

Working with Functions and Graphs

Understanding how to work with functions and their graphical representations is a critical skill in problem-solving. Functions provide a way to model relationships between variables, and graphs help visualize these relationships. Knowing how to interpret graphs, as well as how to manipulate and transform functions, is essential for solving complex problems.

Key Concepts in Functions

To work effectively with functions, it’s important to grasp the following concepts:

• Domain and Range: The domain represents all possible inputs, while the range refers to all possible outputs of the function.
• Types of Functions: Recognize different function types, such as linear, quadratic, and exponential, and understand their behaviors.
• Function Notation: Understand how to express a function using notation like f(x), and how to substitute values into the function to find corresponding outputs.

Graphing Functions

Graphing allows you to visualize the behavior of a function. Here’s how to approach graphing:

1. Identify the function type and its key features (intercepts, slopes, etc.).
2. Plot key points by substituting different values of x into the function.
3. Draw the graph, paying attention to the overall shape and key features of the function.

With practice, graphing functions will become intuitive, and you’ll be able to interpret and analyze them with ease. Whether it’s a simple linear graph or a more complex quadratic curve, mastering this skill is essential for progressing in mathematics.

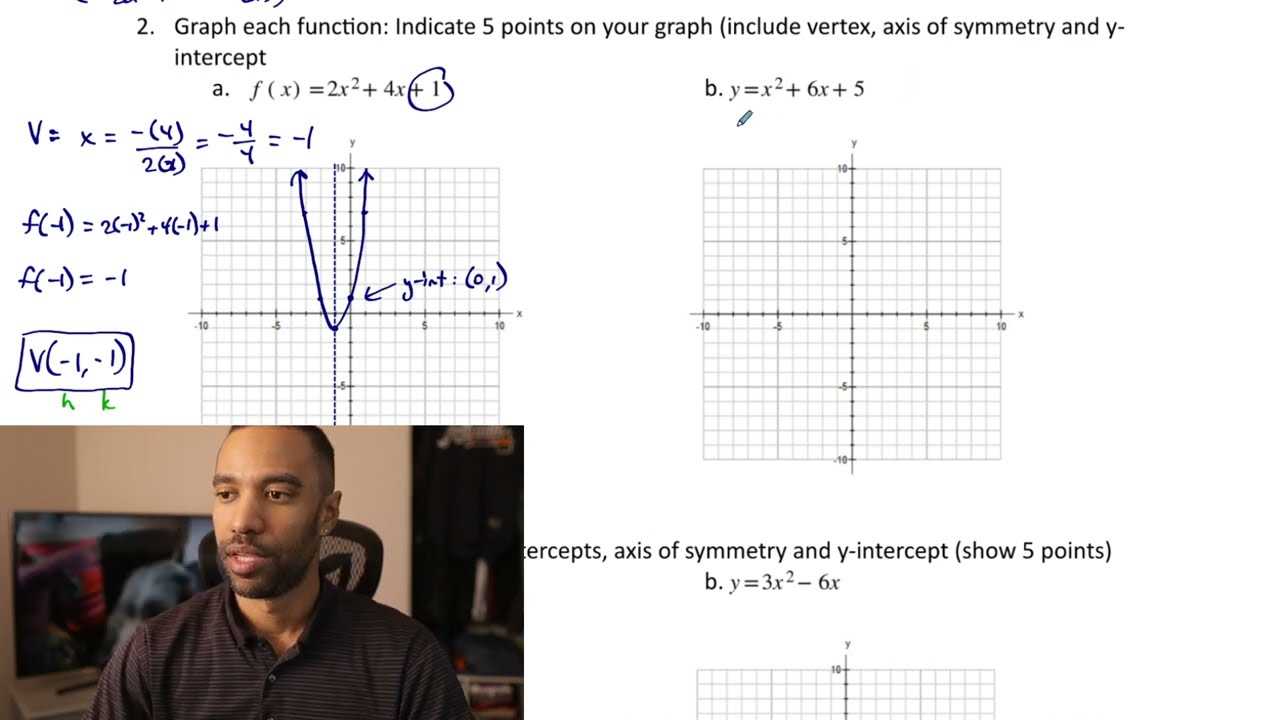
Quadratic Equations and Solutions

Quadratic equations are among the most important concepts in algebra. These equations involve a variable raised to the second power, and they often appear in various real-world problems. To solve these equations effectively, it’s essential to understand different methods and recognize when to use each one. Whether you’re solving for specific values or analyzing the properties of the equation, mastering the techniques is key to success.

Methods to Solve Quadratic Equations

There are several approaches to solving quadratic equations. The most commonly used methods include:

• Factoring: Express the equation as a product of two binomials and solve for the variable.
• Quadratic Formula: Use the formula x = (-b ± √(b² – 4ac)) / 2a to find the roots of the equation.
• Completing the Square: Rearrange the equation so that one side forms a perfect square trinomial, then solve for the variable.

Key Properties of Quadratic Equations

Understanding the properties of quadratic equations is also important for solving them:

1. Discriminant: The discriminant (b² – 4ac) helps determine the nature of the solutions. If it’s positive, there are two real solutions; if it’s zero, there is one real solution; if it’s negative, there are no real solutions.
2. Vertex Form: A quadratic equation can be expressed in vertex form y = a(x – h)² + k, where (h, k) represents the vertex of the parabola.
3. Graphing Quadratics: The graph of a quadratic equation is a parabola. The direction of the parabola (upward or downward) depends on the coefficient of the squared term.

By practicing these methods and understanding the key properties, you’ll be able to solve quadratic equations with confidence and accuracy.

Tips for Solving Word Problems

Word problems often seem intimidating at first, but they can be tackled with the right approach. The key to solving these types of problems is understanding the question, translating the given information into mathematical expressions, and applying the appropriate methods to find the solution. By following a structured process, you can break down complex scenarios into manageable steps.

Step-by-Step Approach

To solve word problems effectively, consider these steps:

1. Read the Problem Carefully: Understand the context and what is being asked. Highlight key information and identify what needs to be found.
2. Identify the Variables: Assign variables to the unknown quantities and define them clearly.
3. Translate Words into Equations: Convert the words into mathematical expressions or equations. Pay attention to keywords like “sum,” “difference,” “product,” and “quotient.”
4. Solve the Equation: Use the appropriate methods to solve for the unknowns.
5. Check the Solution: Once you have the solution, double-check it by plugging it back into the original problem to ensure it makes sense.

Common Mistakes to Avoid

• Misinterpreting the Question: Always ensure you understand what the problem is asking for before attempting to solve it.
• Skipping Units: Be sure to include units in your calculations and answer. Units can provide important context for the problem.
• Forgetting to Check the Answer: It’s crucial to verify your solution to avoid simple errors that can lead to incorrect results.

By practicing these strategies, you can develop a systematic approach to solving word problems and improve your problem-solving skills overall.

Exploring Systems of Equations

Systems of equations involve solving multiple equations simultaneously, where the goal is to find a set of values that satisfy all the equations at once. These systems can represent real-world scenarios, such as determining the intersection points of lines or balancing equations in various applications. Understanding how to solve these systems is crucial for addressing more complex problems that involve several variables.

Methods to Solve Systems of Equations

There are several techniques to solve systems of equations, each useful depending on the structure of the system:

• Graphing: Plot both equations on a coordinate plane and identify the point(s) where the lines intersect. This method works well when the equations are simple and easy to graph.
• Substitution: Solve one equation for one variable and then substitute that expression into the other equation. This method is particularly useful when one of the equations is easily solvable for a single variable.
• Elimination: Add or subtract the equations to eliminate one of the variables, making it easier to solve for the remaining variable. This method is effective when the equations are aligned in such a way that a variable can be easily canceled out.

Key Considerations

When solving systems, it’s important to keep a few key points in mind:

• Consistency: Some systems may have no solution (parallel lines) or infinitely many solutions (coincident lines). Understanding the graphical representation can help you determine the nature of the solutions.
• Accuracy: Always check your solution by substituting the values back into the original equations to ensure they satisfy all conditions.
• Scalability: Systems can involve more than two equations or variables. The methods described above can be extended to larger systems, though they may become more complex.

Mastering these techniques will allow you to confidently solve systems of equations, whether you’re solving for two variables or working with larger systems in more advanced scenarios.

Operations with Polynomials

Polynomials are expressions that consist of variables raised to various powers and are combined using addition, subtraction, and multiplication. Mastering the operations with polynomials is essential for simplifying expressions and solving algebraic problems. Understanding how to perform operations such as addition, subtraction, and multiplication can simplify complex problems and make solving them more straightforward.

Addition and Subtraction of Polynomials

When adding or subtracting polynomials, it’s important to combine like terms. Like terms are terms that have the same variable raised to the same power. Here are the steps to follow:

• Identify like terms: Look for terms with the same variable and exponent.
• Add or subtract the coefficients: Combine the coefficients of like terms while keeping the variables and exponents the same.
• Write the simplified expression: After combining all the like terms, write the final expression in standard form (terms in descending order of exponents).

Multiplication of Polynomials

Multiplying polynomials involves applying the distributive property. When multiplying two binomials or a binomial with a monomial, follow these steps:

• Distribute each term: Multiply each term in one polynomial by every term in the other polynomial.
• Combine like terms: After distributing, combine any like terms that appear in the result.
• Write the result: Simplify the expression by combining all like terms and arranging them in standard form.

By practicing these basic operations, you’ll gain a deeper understanding of how polynomials work and be able to solve more complex algebraic expressions with ease.

Reviewing Rational Expressions

Rational expressions consist of fractions where both the numerator and the denominator are polynomials. Understanding how to manipulate these expressions is essential for solving algebraic problems. Whether simplifying, adding, subtracting, or performing other operations, the key lies in managing the relationship between the numerator and denominator efficiently.

Simplifying Rational Expressions

To simplify a rational expression, it’s important to factor both the numerator and the denominator, then cancel out any common factors. Here’s how:

• Factor both terms: Look for common factors in both the numerator and the denominator and factor them out.
• Cancel out common factors: If the same term appears in both parts, you can cancel it out.
• Rewrite the simplified expression: Once the common factors are removed, rewrite the remaining expression as simplified.

Adding and Subtracting Rational Expressions

When adding or subtracting rational expressions, it’s crucial to have a common denominator. Here’s a step-by-step guide:

1. Identify the least common denominator (LCD): Find the smallest denominator that both fractions can share.
2. Rewrite the fractions with the LCD: Adjust the numerators so they are in terms of the LCD.
3. Perform the operation: Add or subtract the numerators, and keep the denominator the same.
4. Simplify the result: Factor the result if possible and reduce to the simplest form.

By mastering these operations, you will be able to handle complex rational expressions with greater ease and confidence.

Geometry Concepts in Algebra

Understanding the connection between geometric principles and algebraic expressions is essential for solving a wide range of problems. Many algebraic techniques are used to represent and solve geometric concepts, such as calculating the area, perimeter, or volume of shapes, and working with coordinates in the coordinate plane. This intersection allows for a deeper comprehension of both subjects, as algebraic methods are applied to solve geometric problems, and geometric reasoning aids in visualizing algebraic equations.

Using Coordinates in the Coordinate Plane

One of the most important ways geometry and algebra intersect is through the use of the coordinate plane. Points on this plane can be represented as ordered pairs (x, y), which are often used to express the relationship between two variables in an equation. This allows for the visualization of linear equations, curves, and other geometric shapes.

• Plotting points: Each point on the coordinate plane corresponds to a solution of an equation.
• Understanding slope: The slope of a line in the coordinate plane is calculated using the formula m = (y2 – y1) / (x2 – x1), which represents the ratio of vertical change to horizontal change.
• Equation of a line: A straight line in the plane is described by a linear equation, such as y = mx + b, where m is the slope and b is the y-intercept.

Geometry in Quadratic Equations

Quadratic equations, which describe parabolic shapes, have significant geometric interpretations. The solutions to a quadratic equation often correspond to the points where the parabola intersects the x-axis, known as the roots or zeros of the equation.

• Vertex form: The equation of a parabola can be written in vertex form y = a(x – h)^2 + k, where (h, k) represents the vertex, or the highest or lowest point of the curve.
• Graphing quadratics: The graph of a quadratic equation creates a U-shaped curve called a parabola, and understanding the relationship between the equation and its graph is a key skill in both geometry and algebra.

By mastering how geometric concepts are used in algebra, students can not only solve a variety of problems but also gain a greater appreciation for the interconnectivity of different mathematical fields.

Probability and Statistics Review

Probability and statistics are essential tools used to analyze data and make predictions about various situations. In this section, we focus on understanding key concepts related to the likelihood of events occurring, as well as how to interpret and organize data in a meaningful way. Mastering these concepts is crucial for solving real-world problems and making informed decisions based on numerical information.

Understanding Probability

Probability deals with the likelihood of an event happening. It is a way to quantify uncertainty, ranging from 0 (impossible) to 1 (certain). Knowing how to calculate the probability of simple and compound events is crucial for interpreting real-world scenarios, such as predicting weather patterns or analyzing games of chance.

• Simple probability: The probability of a single event is calculated as the ratio of favorable outcomes to the total number of possible outcomes. For example, the probability of rolling a 3 on a fair die is 1/6.
• Compound events: For multiple events happening together, you can use addition or multiplication rules. For example, the probability of rolling a 3 or a 5 is the sum of individual probabilities, while the probability of rolling a 3 and then a 5 on two dice is the product of individual probabilities.
• Independent events: Two events are independent if the occurrence of one does not affect the probability of the other. For example, flipping a coin and rolling a die are independent events.

Statistical Analysis and Interpretation

Statistics is concerned with collecting, organizing, analyzing, and interpreting data. It helps to summarize information, draw conclusions, and make predictions based on sample data. Key concepts in statistics include measures of central tendency, variability, and interpreting graphical data representations.

• Measures of central tendency: These include the mean, median, and mode, which describe the center of a data set. The mean is the average, the median is the middle value, and the mode is the most frequent value.
• Measures of spread: The range, variance, and standard deviation describe how spread out the data is. A large range or high standard deviation indicates that the data points are far apart, while a small range suggests that the data points are close to each other.
• Graphical representations: Data can be represented using various charts, such as bar graphs, histograms, and box plots. These visuals help to identify patterns, trends, and outliers in the data.

By understanding both probability and statistical analysis, you can better interpret data, make predictions, and solve problems based on numerical information. These skills are applicable in a wide range of fields, including science, economics, and everyday decision-making.

Analyzing Exponential Functions

Exponential functions model many natural processes, such as population growth, radioactive decay, and compound interest. These functions are characterized by a constant rate of growth or decay, and understanding their behavior is essential for solving problems in a wide variety of fields. By analyzing the properties and graph of an exponential function, we can predict future outcomes and understand how changes in parameters affect the results.

Key Features of Exponential Functions

Exponential functions have distinct characteristics that set them apart from linear and quadratic functions. These features help to define their behavior and guide the process of solving related problems.

• Exponential growth or decay: Exponential functions can model growth (when the base is greater than 1) or decay (when the base is between 0 and 1). For example, a population increasing at a constant rate follows an exponential growth pattern, while a substance decaying over time follows an exponential decay pattern.
• Base of the function: The base of an exponential function determines the rate of growth or decay. If the base is greater than 1, the function exhibits growth; if it is between 0 and 1, the function shows decay. The base affects the steepness of the graph.
• Horizontal asymptote: The graph of an exponential function typically has a horizontal asymptote, meaning that as the input values approach infinity, the output values get closer and closer to a specific value, but never quite reach it. For exponential decay, this asymptote is usually the x-axis (y = 0).
• Rate of change: The rate of change in an exponential function is constant when expressed in terms of percentages, which means the function grows or decays by a fixed percentage over equal time intervals.

Solving Exponential Equations

When solving exponential equations, the goal is to isolate the variable, typically using logarithms or properties of exponents. Below are steps to solve common exponential equations:

• Equations with the same base: If both sides of the equation have the same base, set the exponents equal to each other. For example, in the equation 2^x = 2^5, we can directly conclude that x = 5.
• Using logarithms: When the bases are not the same, take the logarithm of both sides. For instance, to solve 5^x = 125, take the logarithm of both sides and solve for x: x = log(125) / log(5).
• Exponential decay models: In situations where you are dealing with decay, such as population decrease or depreciation of an asset, apply the exponential decay formula and solve for the variable of interest, often time or initial value.

Understanding how to analyze and solve exponential functions equips you to handle real-world problems involving growth and decay. By mastering the key features of these functions, you can interpret the results and make accurate predictions based on the mathematical models.

Understanding Inequalities and Solutions

Inequalities describe relationships between expressions where one side is not necessarily equal to the other. These relationships are crucial for representing a variety of situations, such as limitations, conditions, and ranges of possible outcomes. By solving inequalities, we can determine a set of values that satisfy the conditions, and interpreting these solutions provides insight into practical problems across many fields.

Types of Inequalities

Inequalities can take several forms, each with distinct characteristics and methods of solution:

• Linear Inequalities: These involve expressions where the variable is raised to the first power, often resulting in a solution that can be represented on a number line.
• Quadratic Inequalities: These involve variables squared, and their solutions typically form a region on the graph shaped like a parabola.
• Rational Inequalities: These involve fractions with variables in the denominator, often requiring special attention to avoid division by zero.

Solving Inequalities

Solving inequalities involves isolating the variable, just like equations, but with some key differences. It’s important to keep in mind that multiplying or dividing both sides by a negative number reverses the inequality direction. Here’s a general approach to solving linear inequalities:

1. Isolate the variable: Simplify both sides of the inequality by adding, subtracting, multiplying, or dividing.
2. Reverse the sign when multiplying or dividing by a negative number: This step is crucial in maintaining the correct inequality.
3. Express the solution: The solution is often written in interval notation or shown on a graph.

For example, solving 2x + 3 involves the following steps:

Step 1: Subtract 3 from both sides	2x
Step 2: Divide both sides by 2	x

Thus, the solution is x , which means any value less than 2 satisfies the inequality.

Important Formulas to Remember

Formulas are essential tools in solving various types of problems, helping to simplify complex calculations and provide a structured approach to finding solutions. By mastering these key equations, you’ll be able to tackle a wide range of topics effectively. Below are some fundamental formulas that are often used in algebra, geometry, and other related areas.

Algebraic Formulas

• Quadratic Formula: Used to solve quadratic equations of the form ax² + bx + c = 0. The solution is given by: x = (-b ± √(b² – 4ac)) / 2a
• Slope Formula: For finding the slope of a line between two points (x₁, y₁) and (x₂, y₂): m = (y₂ – y₁) / (x₂ – x₁)
• Point-Slope Form: Used to write the equation of a line given a point (x₁, y₁) and the slope m: y – y₁ = m(x – x₁)

Geometric Formulas

• Area of a Triangle: A = 1/2 × base × height
• Area of a Rectangle: A = length × width
• Perimeter of a Rectangle: P = 2 × (length + width)
• Area of a Circle: A = πr² (where r is the radius)
• Circumference of a Circle: C = 2πr

Familiarizing yourself with these formulas will not only enhance your problem-solving skills but also help you apply them correctly in various scenarios, making them indispensable tools for success in this subject.

Test-Taking Strategies for Success

Approaching assessments with the right mindset and strategies can significantly improve your performance. While understanding the content is essential, having effective test-taking techniques can help you maximize your results. Here are some key strategies to keep in mind when preparing for and taking a test.

• Read Instructions Carefully: Ensure you understand what is being asked before attempting to answer any questions. This can help you avoid simple mistakes and ensure you address each part of the question.
• Manage Your Time: Allocate enough time for each section, but also leave room for review. If you are stuck on a question, move on and come back to it later.
• Start with the Easy Questions: Tackle the questions you are most confident about first. This will boost your confidence and help you accumulate points quickly.
• Eliminate Incorrect Options: When faced with multiple-choice questions, rule out obviously wrong answers. This increases your chances of guessing correctly if needed.
• Check Your Work: If time permits, always go back and review your answers. Look for calculation errors, misinterpretations, or overlooked details.
• Stay Calm: Test anxiety can impair your ability to think clearly. Take deep breaths and stay focused. A calm approach allows you to think more logically and make fewer mistakes.

By incorporating these strategies, you can enhance your test performance and approach assessments with greater confidence and efficiency. Effective time management, careful reading, and a calm mindset will go a long way toward ensuring success.