Semester Exam Review Algebra 2 Answers Guide

As you approach the final stages of your course, it’s essential to revisit the key concepts that will be tested. Whether you’re solving complex equations, working with functions, or simplifying expressions, understanding the foundational principles will ensure you perform at your best. Strengthening your skills in these areas can make a significant difference in how you tackle each problem.

Effective preparation requires more than just memorizing formulas. It involves honing problem-solving techniques and practicing various question types. By focusing on common challenges and recognizing patterns in problems, you can approach your assessment with confidence and clarity. The key to success is persistence and practice, ensuring you’re ready for any mathematical task that comes your way.

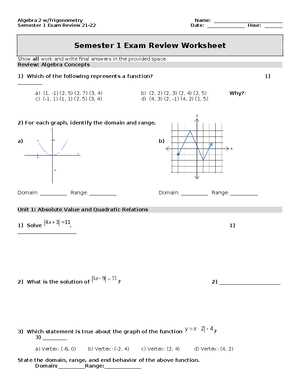
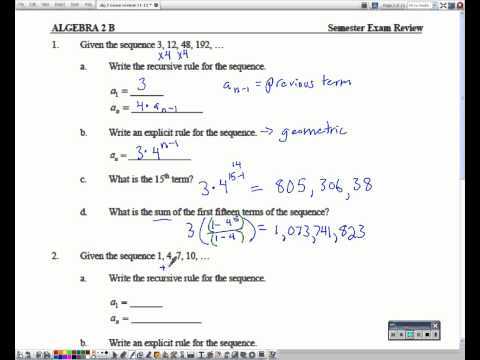
Semester Exam Review Algebra 2 Answers

When preparing for a challenging math assessment, focusing on key problem types and mastering the techniques needed to solve them is crucial. The goal is to develop a strong grasp of the concepts and be able to apply them efficiently under timed conditions. This section will help you identify the essential topics and provide strategies for tackling various types of questions with confidence.

Start by reviewing the core topics that frequently appear in these types of assessments. The following areas are fundamental to your success:

Quadratic Equations: Know how to solve using factoring, completing the square, and the quadratic formula.
Functions: Understand their properties and how to graph linear, exponential, and polynomial functions.
Rational Expressions: Practice simplifying and solving equations that involve fractions with variables.
Systems of Equations: Be prepared to solve systems using substitution, elimination, and graphical methods.
Inequalities: Learn how to solve and graph both linear and quadratic inequalities.

To help reinforce your understanding, make sure to practice problems that cover a wide range of difficulty levels. Here are a few tips to guide your study sessions:

Practice Regularly: Consistent practice will improve your problem-solving speed and accuracy.
Work on Word Problems: These often require you to apply multiple concepts and techniques at once.
Check Your Work: Take the time to verify your solutions and ensure no mistakes have been made during the process.
Use Study Groups: Collaborating with peers can help reinforce understanding and provide new insights.

By focusing on these areas and incorporating the recommended strategies, you’ll be well-prepared to handle any challenge that comes your way during the assessment. The key is to stay organized, review thoroughly, and approach each problem systematically.

Key Concepts to Focus On

When preparing for a mathematics assessment, it’s important to prioritize the most critical topics that are essential for solving a variety of problems. By concentrating on the fundamental concepts, you can improve your ability to tackle a wide range of questions with confidence and precision. These core ideas form the foundation for more complex problem-solving tasks and should be mastered before moving on to advanced techniques.

Here are some of the key areas to concentrate on:

Equations and Inequalities: Understanding how to manipulate and solve both linear and quadratic equations is essential. Pay attention to systems of equations and how to solve them using different methods like substitution and elimination.
Functions and Graphing: Be familiar with the different types of functions, such as linear, exponential, and polynomial. Practice plotting and interpreting their graphs to understand their behavior and properties.
Factoring and Simplification: Mastering factoring techniques and simplifying expressions will help you solve problems more efficiently. This includes factoring trinomials, difference of squares, and grouping methods.
Rational Expressions: Be comfortable working with fractions that involve variables. Know how to simplify, add, subtract, multiply, and divide rational expressions, and solve equations that contain them.
Word Problems: These types of questions test your ability to apply mathematical concepts in real-world situations. Practice translating word problems into mathematical expressions and equations.

Focusing on these key areas will give you a solid foundation for approaching a variety of problems. It’s important to practice regularly and work through problems of varying difficulty to ensure you’re prepared for all aspects of the assessment.

Understanding Algebra 2 Equations

Grasping the fundamentals of mathematical equations is key to solving a wide range of problems efficiently. Whether you’re dealing with linear, quadratic, or more complex expressions, understanding how to manipulate and solve these equations is crucial. Mastering these skills will allow you to approach problems with confidence and apply the correct methods to find solutions.

Start by familiarizing yourself with the different types of equations and their specific properties:

Linear Equations: These involve variables with exponents of one and can typically be solved by isolating the variable on one side. Ensure you practice solving for x and interpreting solutions in the context of real-world problems.
Quadratic Equations: These involve variables raised to the power of two and are often solved using methods like factoring, completing the square, or using the quadratic formula. Understanding how to recognize and solve these types of problems is vital.
Exponential Equations: These equations include variables in the exponent position and often require logarithmic methods to solve. Knowing how to apply logarithms is essential for working with such problems.
Rational Equations: Equations involving fractions with variables in the numerator or denominator. It’s important to simplify these expressions and avoid undefined values when solving.

As you solve these equations, focus on the techniques that will allow you to isolate the variable, factor correctly, and check your solutions. Regular practice with varied examples will strengthen your understanding and make solving these problems more intuitive.

Common Mistakes in Algebra 2 Exams

Even the most prepared students can make mistakes when tackling challenging math problems. Often, these errors are simple oversights but can have a significant impact on the final result. By recognizing and understanding the most frequent mistakes, you can avoid them and improve your overall performance. Developing attention to detail and applying consistent problem-solving strategies will help you minimize these errors during assessments.

Here are some of the most common mistakes to watch out for:

Sign Errors: A common mistake is mishandling negative signs when adding or subtracting terms. Always double-check your work when working with positive and negative numbers.
Forgetting to Simplify: It’s easy to overlook simplifying expressions, especially in complex equations. Always ensure that you’ve simplified as much as possible before moving on to the next step.
Incorrectly Applying Formulas: Misapplying formulas or using the wrong method for certain types of problems can lead to incorrect results. Make sure you’re familiar with the appropriate formulas for each equation type.
Skipping Steps: Rushing through problems can result in skipped steps, leading to errors in the final solution. Take your time and solve each problem step by step.
Overlooking Units in Word Problems: Failing to convert or keep track of units in real-world problems can lead to incorrect answers. Pay careful attention to the units and what they represent.

By being aware of these pitfalls, you can take proactive steps to avoid them. Double-check your calculations, take your time with each problem, and practice regularly to build confidence and accuracy.

How to Solve Quadratic Equations

Solving equations that involve a variable raised to the second power is a fundamental skill in mathematics. These types of problems are common and can be approached in several different ways, depending on the equation’s form. By mastering the various methods, you can quickly identify the best strategy for solving each problem and reach the correct solution.

Factoring Method

The factoring method is one of the most straightforward techniques for solving quadratic equations. To use this approach, first express the equation in standard form, ax² + bx + c = 0. Then, factor the quadratic expression into two binomials. Once factored, set each factor equal to zero and solve for the variable. This method works well when the equation factors neatly into two terms.

Quadratic Formula

If the equation cannot be easily factored, the quadratic formula provides a reliable solution. The formula is x = (-b ± √(b² – 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation. By substituting the values of a, b, and c into the formula, you can find the roots of the equation, whether they are real or complex.

Using either of these methods, you’ll be able to solve quadratic equations effectively and apply the solutions to a variety of problems. Practicing both approaches will help you become more efficient and accurate when dealing with these types of equations.

Working with Polynomial Functions

Polynomial functions are an essential part of advanced mathematics and often appear in a wide range of problems. These functions are made up of terms with variables raised to various powers, and their behavior can be analyzed by studying their structure and the relationships between the terms. Understanding how to work with polynomials is crucial for solving more complex equations and for understanding how these functions behave on a graph.

When working with polynomial functions, it’s important to focus on the following key aspects:

Identifying Degree and Leading Coefficient: The degree of the polynomial tells you the highest power of the variable, while the leading coefficient is the number in front of that term. These two elements help determine the general behavior of the function.
Operations with Polynomials: Addition, subtraction, multiplication, and division are fundamental operations you’ll need to perform when working with polynomials. Knowing how to combine terms and factor polynomials is essential.
Factoring Polynomials: Factoring is a key skill when solving equations involving polynomials. Understanding how to break down complex expressions into simpler binomials or other factors can simplify the problem-solving process.
Graphing Polynomial Functions: Understanding how the degree and leading coefficient affect the shape and direction of the graph is crucial. For example, polynomials with even degrees have specific end behaviors, while those with odd degrees behave differently at both ends.
Finding Roots and Zeros: Solving for the values of x that make the polynomial equal to zero (the roots or zeros) is an important skill. You can find these by factoring or using numerical methods like synthetic division or the Rational Root Theorem.

By focusing on these areas and practicing regularly, you’ll develop a strong understanding of polynomial functions and be able to solve a wide range of problems efficiently. These concepts will be key in tackling more complex mathematical challenges.

Mastering Rational Expressions

Working with rational expressions involves understanding how to manipulate fractions that contain variables. These expressions can seem complex at first, but with a solid grasp of fundamental principles, you can simplify, add, subtract, multiply, and divide them effectively. Mastering these skills is essential for solving a wide variety of problems in advanced mathematics.

Simplifying Rational Expressions

To simplify a rational expression, begin by factoring both the numerator and the denominator, if possible. Once the expression is factored, look for common factors in both parts and cancel them out. This will reduce the expression to its simplest form. Remember that simplifying an expression is crucial for making calculations easier and for avoiding unnecessary complexity.

Operations with Rational Expressions

When performing operations with rational expressions, it’s important to follow the correct steps:

Addition and Subtraction: To add or subtract rational expressions, you must first find a common denominator. After that, you can combine the numerators and simplify the resulting expression.
Multiplication: To multiply rational expressions, simply multiply the numerators together and the denominators together. Then, simplify the result by canceling out any common factors.
Division: Dividing one rational expression by another is equivalent to multiplying the first expression by the reciprocal of the second. Again, simplify the resulting expression where possible.

By practicing these techniques and mastering the rules for handling rational expressions, you will be able to solve more complex problems with confidence and accuracy. Regular practice is key to becoming proficient in manipulating and simplifying these types of expressions.

Tips for Graphing Functions

Graphing mathematical functions is a fundamental skill that helps visualize relationships between variables. Understanding the key characteristics of a function and how to interpret them on a graph can make the process much more efficient. By applying the right strategies, you can plot functions accurately and gain deeper insights into their behavior.

Key Steps for Graphing

Before plotting a function, it’s important to follow these essential steps:

Identify the Function Type: Recognizing whether you’re dealing with a linear, quadratic, exponential, or other type of function will guide you in understanding its general shape and behavior.
Find Key Points: Always determine key points like intercepts, critical points, and asymptotes. These points will serve as anchors when drawing the graph.
Choose a Range of Values: Select a range of values for the variable and plug them into the function to find corresponding outputs. Plot these points on the coordinate plane to form a clear representation of the function.

Common Graphing Tips

Here are additional tips to improve the accuracy and clarity of your graphs:

Use Symmetry: Many functions, especially quadratics, are symmetric. Recognizing symmetry can save you time and help you accurately complete half of the graph, reflecting it to the other side.
Label Important Points: Clearly label intercepts, turning points, and any other important points on your graph. This will help in interpreting the graph and verifying your work.
Check End Behavior: Pay attention to the behavior of the function as the values of the variables increase or decrease. Understanding the end behavior can help predict the direction the graph will take.
Scale the Axes Appropriately: Make sure the axes are scaled correctly to accommodate the function’s range. A well-chosen scale will make your graph more readable and accurate.

By practicing these strategies, you’ll improve your graphing skills and be able to plot functions more quickly and accurately. Consistent practice and understanding key function behaviors are the keys to mastering graphing techniques.

Understanding Systems of Equations

Solving systems of equations involves finding values for variables that satisfy multiple equations simultaneously. These problems arise when you need to determine where two or more mathematical relationships intersect. Approaching these systems systematically can make solving them more straightforward and help you understand the connections between different expressions.

There are several methods to solve systems of equations, each suited to different types of problems. The key is to recognize the method that will simplify the process and lead you to the solution quickly.

Graphing Method: One way to solve a system of equations is to graph both equations on the same coordinate plane and find the point of intersection. This method works well for visualizing the solution but may be less precise for complex systems.
Substitution Method: In this approach, solve one of the equations for one variable and substitute that expression into the other equation. This can help eliminate one variable and simplify the system to a single equation with one unknown.
Elimination Method: This technique involves adding or subtracting the equations to eliminate one of the variables. It is often used when the coefficients of one variable are already the same or can be easily made the same through multiplication.

By practicing these techniques, you can improve your ability to solve systems of equations efficiently and apply this knowledge to more complex problems in various areas of mathematics.

Strategies for Simplifying Expressions

Simplifying mathematical expressions is an essential skill that helps to make complex problems more manageable. The goal is to rewrite the expression in a more concise and efficient form, often by combining like terms, factoring, or applying mathematical rules. With the right techniques, you can reduce complicated expressions to simpler forms that are easier to work with in equations and problems.

Here are some key strategies to help simplify expressions effectively:

Combine Like Terms: One of the first steps in simplifying an expression is to group and combine terms that have the same variables raised to the same powers. This eliminates redundancy and makes the expression more compact.
Factor Common Factors: Look for common factors in the terms of the expression. Factoring out the greatest common factor (GCF) can make the expression simpler and often reveals a more manageable form.
Apply Distribution: Use the distributive property to eliminate parentheses and combine terms. This helps break down more complex expressions and allows you to simplify them step-by-step.
Reduce Fractions: When dealing with rational expressions, simplify by canceling out common factors in the numerator and denominator. This step is crucial for making fractions easier to work with.
Use Exponent Rules: Applying exponent rules, such as the power of a product or quotient rule, can significantly simplify expressions with exponents. This includes rules for multiplying and dividing terms with exponents, as well as raising a power to a power.

By mastering these strategies, you’ll be able to handle a wide range of expressions with confidence, making them more manageable and easier to solve in different mathematical contexts.

Factoring Techniques You Need

Factoring is a powerful tool for simplifying mathematical expressions and solving equations. By breaking down complex expressions into simpler components, you can make problems easier to solve and understand. Mastering various factoring methods will give you the flexibility to tackle a wide range of problems efficiently and accurately.

Key Factoring Methods

There are several essential techniques to keep in mind when factoring. Each method has its specific use depending on the form of the expression you’re dealing with:

Factoring Out the Greatest Common Factor (GCF): Always start by identifying and factoring out the greatest common factor of all terms in the expression. This reduces the expression to a simpler form and can reveal further factoring opportunities.
Factoring Trinomials: For quadratic trinomials, use methods such as trial and error or the “ac method” to find two numbers that multiply to the product of the leading coefficient and constant, and add up to the middle coefficient. This will help split the middle term and factor the trinomial.
Difference of Squares: When you encounter an expression in the form of a² – b², recognize it as a difference of squares. This can be factored into (a + b)(a – b), a quick and efficient method for simplification.

Advanced Factoring Techniques

Once you’re comfortable with basic factoring methods, there are a few more advanced techniques to handle more complex expressions:

Factoring Perfect Square Trinomials: When you have an expression like a² + 2ab + b², you can factor it as (a + b)². Recognizing these patterns can speed up the factoring process.
Factoring by Grouping: If an expression has four terms, you can often factor by grouping. This involves splitting the expression into two groups, factoring each group separately, and then factoring out the common binomial factor.

Mastering these factoring techniques will not only help you simplify expressions but also provide the foundation for solving more complex equations and mathematical problems efficiently.

Solving Exponential and Logarithmic Problems

Exponential and logarithmic equations are crucial in many areas of mathematics, often used to model real-world phenomena like population growth, radioactive decay, and financial calculations. Solving these problems requires understanding the relationship between exponents and their inverse, logarithms. By mastering the techniques for solving these types of equations, you can tackle complex problems with ease and precision.

Exponential equations involve variables in the exponent, while logarithmic equations are the inverse, with the variable inside the logarithmic function. Understanding how to manipulate these forms is essential to finding the unknowns in both types of equations.

Solving Exponential Equations: To solve an exponential equation, first ensure that both sides of the equation have the same base. If they do, you can set the exponents equal to each other and solve for the variable. If the bases are different, you may need to take the logarithm of both sides to simplify the equation.
Solving Logarithmic Equations: When solving logarithmic equations, the goal is to isolate the logarithmic term. Once the logarithmic term is isolated, rewrite the equation in exponential form to solve for the variable. Understanding the properties of logarithms, such as the product, quotient, and power rules, is key to simplifying and solving these equations.
Using Logarithmic Properties: Apply the logarithmic properties to simplify the expression and solve for the unknown. For example, use the product rule log(a) + log(b) = log(ab) or the power rule n * log(a) = log(a^n) to manipulate the equation into a more solvable form.

By practicing these techniques, you can confidently solve exponential and logarithmic equations and apply them to a variety of problems. Whether it’s dealing with growth rates or analyzing data trends, these methods are invaluable for finding solutions efficiently.

Preparing for Word Problems

Word problems are an essential part of mathematical problem-solving, requiring the ability to translate real-world scenarios into mathematical expressions. The key to solving these problems lies in understanding the context and identifying the relevant information. By breaking down the problem step by step and choosing the right mathematical tools, you can solve even the most complex word problems effectively.

To approach word problems successfully, follow a systematic process that includes interpreting the question, identifying variables, setting up equations, and solving. Practicing this process will help you become more confident in approaching word problems of any kind.

Step	Description
Step 1: Understand the Problem	Read the problem carefully to determine what is being asked. Identify the known and unknown quantities, and highlight the key information.
Step 2: Define Variables	Assign variables to the unknown quantities, ensuring that you clearly understand what each variable represents.
Step 3: Translate to an Equation	Convert the information from the word problem into a mathematical equation or system of equations.
Step 4: Solve the Equation	Use appropriate techniques, such as solving for variables or simplifying expressions, to find the solution.
Step 5: Interpret the Solution	Once the solution is found, make sure to interpret it in the context of the original problem to ensure that the answer makes sense.

With regular practice and a methodical approach, solving word problems becomes much easier. By following these steps and staying organized, you can tackle any word problem confidently and efficiently.

Reviewing Inequalities in Algebra

Understanding the behavior of relationships between numbers is crucial in solving mathematical problems. Inequalities play an important role in this, as they allow us to express conditions where values are not strictly equal but instead follow certain comparative relationships. Being comfortable with manipulating and interpreting these expressions is key to solving a wide variety of problems in mathematics.

Types of Inequalities

There are several different types of inequalities, each with its own rules for solving and interpreting solutions. The most common inequality symbols include:

<: less than
>: greater than
≤: less than or equal to
≥: greater than or equal to
≠: not equal to

Each of these symbols helps to describe the relationship between two expressions, and understanding them allows you to solve problems more effectively. Pay close attention to the symbol used when solving an inequality, as it dictates the method of solving and the interpretation of the solution.

Solving and Graphing Inequalities

When solving inequalities, the same basic principles apply as with equations, but there are a few important differences. One key rule to remember is that when multiplying or dividing both sides of an inequality by a negative number, the direction of the inequality sign must be reversed.

Graphing the solution to an inequality on a number line can also help visualize the solution set. Open and closed circles are used to indicate whether the endpoints are included in the solution set. An open circle represents that the number is not included, while a closed circle indicates that the number is part of the solution.

By practicing these techniques, you can gain confidence in solving inequalities and applying them to a wide range of mathematical problems.

Using the Discriminant in Quadratics

When dealing with quadratic equations, determining the nature of the solutions is an important step. The discriminant, a specific part of the quadratic formula, helps us understand whether the solutions will be real, complex, or repeated. By analyzing the value of the discriminant, we can gain valuable insights into the behavior of the equation without actually solving it completely.

The discriminant is represented by the expression under the square root in the quadratic formula: b² – 4ac. The value of this expression dictates the number and type of solutions the equation will have:

If b² – 4ac > 0, the equation has two distinct real solutions.
If b² – 4ac = 0, there is exactly one real solution (also called a repeated or double root).
If b² – 4ac < 0, the equation has two complex solutions, which are conjugates of each other.

Understanding the discriminant can save time when solving quadratic equations, as it allows us to predict the nature of the roots before proceeding with the full calculation. This concept is useful in various applications, such as graphing parabolas and solving real-world problems involving quadratic relationships.

Applications of Algebra 2 Concepts

The skills learned in advanced mathematics can be applied to a wide range of real-world situations. These concepts extend beyond the classroom and are used to model and solve problems in science, economics, engineering, and even everyday life. Understanding how to manipulate equations, functions, and graphs allows for a deeper comprehension of the world around us, from predicting outcomes to analyzing patterns.

Real-World Applications

Here are some practical applications of the concepts learned in advanced mathematics:

Concept	Application
Quadratic Equations	Used in projectile motion to model the height of an object over time, such as when calculating the trajectory of a ball or the flight path of a rocket.
Exponential Functions	Commonly used in population growth models, as well as in finance for calculating compound interest or growth of investments.
Systems of Equations	Applied in various fields such as economics for supply-demand models, as well as in engineering for analyzing circuits or mechanical systems.
Logarithms	Important in measuring the intensity of earthquakes, sound levels, and the pH of substances, as well as in finance for calculating depreciation and loan payments.

Benefits in Problem Solving

By applying these mathematical concepts to real-life scenarios, individuals can solve complex problems and make informed decisions. Whether it’s optimizing a business strategy, understanding scientific data, or simply making sense of everyday occurrences, the power of advanced mathematical reasoning is invaluable. With practice, these skills become essential tools for addressing a wide range of challenges across various fields.

Time Management for Algebra Exams

Effective time management plays a crucial role in achieving success during a test. When tackling mathematical problems, it’s important to allocate time wisely to each question, ensuring that enough focus is given to all parts of the test. Having a strategy in place can reduce stress, increase confidence, and lead to better performance. By following specific time-saving techniques, you can make the most out of your allotted time and tackle each problem efficiently.

Creating a Time Management Plan

Here are some key tips to help manage your time effectively during a math test:

Know the test structure: Before the test, familiarize yourself with the types of problems that will appear. This will help you allocate time appropriately based on the difficulty and length of each section.
Prioritize easier questions: Begin with questions that you find the most straightforward. This will help you build momentum and boost your confidence as you progress through the test.
Set a time limit for each question: Decide on a maximum amount of time to spend on each problem. If you’re stuck, move on to the next one and come back later if time allows.
Leave room for review: Always set aside some time at the end of the test to review your answers, double-check your work, and make sure that you haven’t missed anything important.

Improving Efficiency

To improve your speed and accuracy, it’s essential to practice time management regularly. Here are a few additional strategies:

Practice under timed conditions: Simulate the testing environment by practicing with timed quizzes or past problems. This will help you become more familiar with working under pressure and improve your pacing.
Use shortcuts and formulas: Memorize essential formulas and methods to quickly apply them when needed. This will save you time on calculations and ensure that you’re solving problems more efficiently.
Stay calm and focused: Stress can negatively impact your ability to solve problems quickly. Take deep breaths and stay calm, especially when facing challenging questions. A clear mind helps in making better decisions during the test.

How to Check Your Work

Reviewing your work thoroughly is an essential step to ensure the accuracy and completeness of your solutions. Often, small errors can slip through unnoticed during the first pass, so it’s important to double-check your calculations, reasoning, and answers. A methodical approach to checking your work can save you from missing crucial details and help improve your final performance.

Steps to Effectively Review Your Solutions

Here are some strategies you can follow to check your work efficiently:

Revisit the Problem Statement: Ensure that you understand the question correctly before diving into the review process. Double-check the problem to make sure you haven’t overlooked any specific requirements or instructions.
Recalculate Your Answers: Go through your steps again to verify the results. Pay close attention to each calculation and operation, as even small arithmetic mistakes can affect your final answer.
Check for Common Mistakes: Look out for frequent errors such as sign mistakes, misplacing decimal points, or misunderstanding the order of operations. These mistakes can be easily overlooked but can have a significant impact on your solution.
Use a Different Method: If possible, try solving the problem using an alternative approach or method. A different perspective can often reveal any inconsistencies or mistakes in your original solution.

Tips for a Thorough Review

To ensure a more comprehensive review, keep these tips in mind:

Check Units and Labels: If your problem involves units or variables, ensure that you’ve used the correct ones throughout. Pay attention to any conversions and verify that your units align correctly in the final result.
Look for Logical Consistency: Review your reasoning and ensure each step logically follows the previous one. If something seems unclear or inconsistent, take a moment to reassess that part of your solution.
Leave Time for the Final Check: Allocate time towards the end of the test for a full review. Having a few minutes to check all your answers will give you the opportunity to spot any errors or incomplete steps before submitting your work.