
Geometry can often be challenging, especially when dealing with specific shapes and their unique characteristics. When exploring quadrilaterals, it’s important to understand the distinct features that set each type apart. This section delves into the fundamental principles that govern these figures, helping learners to recognize and solve related problems effectively.
By examining how certain sides, angles, and diagonals interact within these shapes, you will gain a deeper understanding of their structure. Through problem-solving exercises, you’ll learn to apply these concepts, enhancing your ability to identify and work with them in different contexts.
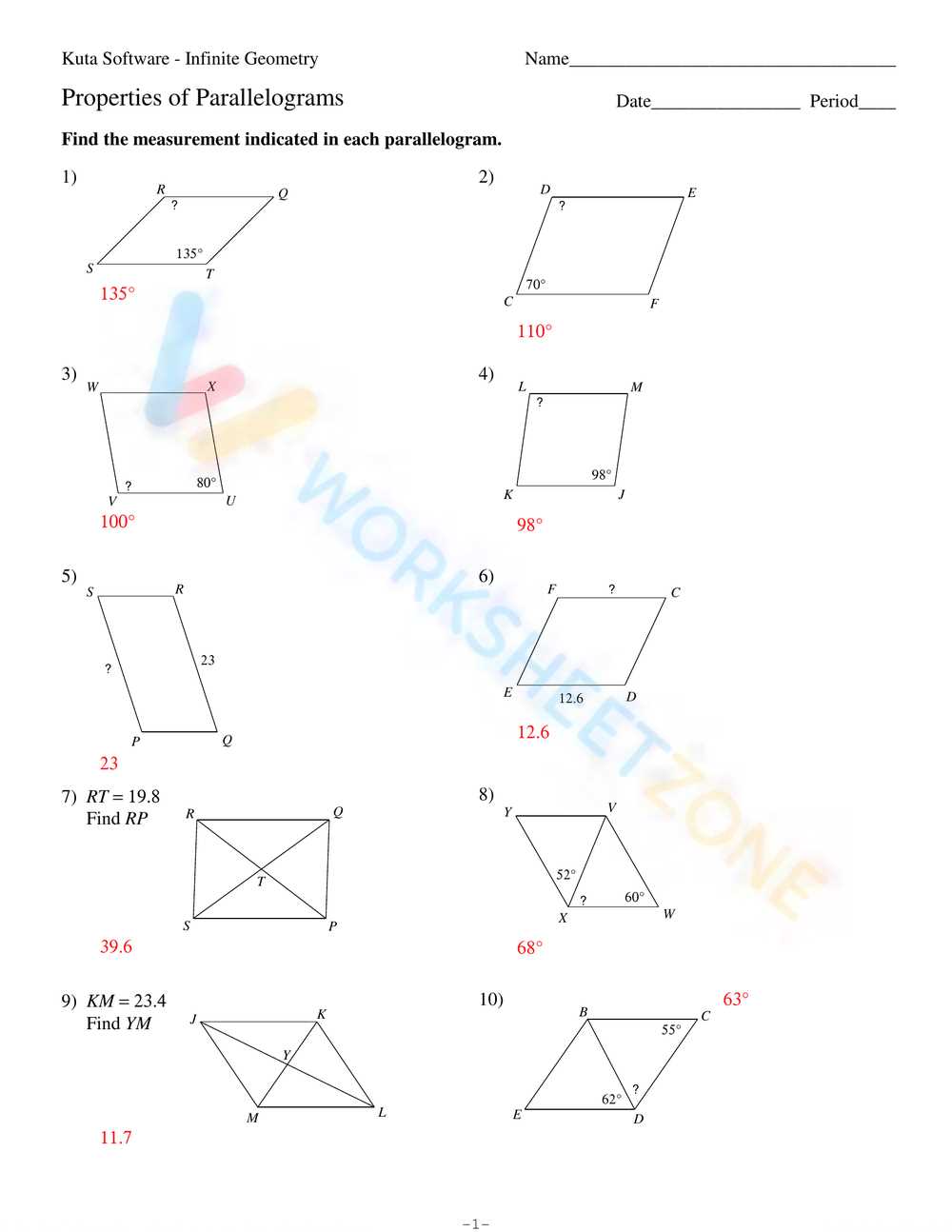
Properties of Parallelograms Worksheet Answers
Understanding the fundamental characteristics of specific quadrilaterals is crucial for solving geometry problems. In this section, we will explore key aspects of these shapes and provide solutions to common exercises that involve calculating angles, sides, and diagonals. The goal is to break down complex questions into manageable steps, ensuring clarity and accuracy in the problem-solving process.
Key Features of These Shapes
Each shape has distinct qualities that must be understood to effectively tackle any related questions. The main features to focus on include:
- Opposite sides being equal in length
- Opposite angles being congruent
- Diagonals that bisect each other
- Adjacent angles summing to 180 degrees
Steps for Solving Common Problems
When approaching problems that involve these shapes, follow these essential steps:
- Identify the given information from the problem.
- Use the known relationships between sides, angles, and diagonals to establish connections.
- Apply appropriate formulas, such as those for calculating area or finding unknown side lengths.
- Double-check your results by verifying each step logically.
By practicing these strategies, you can gain confidence in solving similar geometry problems, reinforcing your understanding of shape properties and their applications.
Understanding Parallelograms in Geometry
In geometry, specific quadrilaterals have unique characteristics that help distinguish them from other shapes. These figures have important properties that govern the relationships between their sides, angles, and diagonals. By understanding these key traits, learners can solve various geometric problems more effectively and recognize these shapes in different contexts.
Key Features of These Quadrilaterals
The defining qualities of these shapes make them an essential topic in geometry. Key aspects include:
- Opposite sides are parallel and equal in length.
- Opposite angles are congruent.
- Diagonals bisect each other at their midpoint.
- Adjacent angles are supplementary, meaning their sum equals 180 degrees.
Recognizing These Shapes in Various Problems
When encountering these shapes in exercises, it’s essential to look for specific clues. Here are some steps to identify them:
- Check if opposite sides are parallel.
- Verify that opposite sides are of equal length.
- Look for angles that match in pairs.
- Examine diagonals to ensure they divide the shape evenly.
By identifying these features, it becomes easier to understand the structure and solve problems related to these specific quadrilaterals. Recognizing these key characteristics will aid in applying the right methods to compute various geometric quantities.
Key Properties of Parallelograms Explained

Understanding the essential characteristics of specific quadrilaterals is crucial for solving geometry problems. These figures have several unique features that influence the relationships between their sides, angles, and diagonals. In this section, we will break down these fundamental traits, which are key to recognizing and working with these shapes in mathematical problems.
One of the most important aspects is that opposite sides are not only equal in length but also run parallel to each other. This parallelism creates a balanced structure, ensuring that angles on the same side of the shape remain congruent. Additionally, the diagonals of these figures have a special relationship, as they bisect each other at their midpoint, dividing the shape symmetrically. Understanding these traits is essential for accurately solving any related geometric tasks.
How to Identify Parallelograms

Recognizing specific quadrilaterals in geometry involves looking for key traits that define their structure. These figures share distinct characteristics that set them apart from other types of quadrilaterals. By understanding these defining features, it becomes easier to identify them in both visual diagrams and problem-solving tasks.
Key Identification Clues
Here are the most important indicators to look for when identifying these shapes:
- Parallel Sides: The opposite sides of these shapes must be parallel to one another.
- Equal Length Sides: Opposite sides not only run parallel but are also equal in length.
- Angle Consistency: Opposite angles are congruent, meaning they are identical in size.
Visual Cues to Look For
When visually analyzing a shape, these clues help confirm its identity:
- Check if the figure has two pairs of opposite sides that appear to run in the same direction.
- Look for parallel lines or marks indicating that opposite sides are equal in length.
- Ensure the angles match across from each other.
By recognizing these key visual and mathematical clues, you can confidently identify these specific quadrilaterals in a variety of geometric problems.
Solving Parallelogram Problems Step by Step
To tackle geometry problems involving specific quadrilaterals, it’s essential to approach them methodically. Each problem can be broken down into smaller steps that allow for a clear path to the solution. By following a structured approach, you can efficiently solve for unknown values such as side lengths, angles, or areas, using the relationships that define these shapes.
Step 1: Analyze the Given Information
Start by carefully reading the problem and identifying all the known values. These could include side lengths, angles, or other geometric properties that are provided. Understanding what is already given is crucial for determining the relationships between different elements in the shape.
Step 2: Apply Relevant Formulas
Once the known values are identified, the next step is to apply the appropriate geometric formulas. For example, if calculating area, you might use the formula involving base and height. If finding missing side lengths, look for parallelism and equal-length side relationships.
In some cases, you may need to use additional properties, such as the fact that opposite angles are congruent or that the diagonals bisect each other. Apply these rules step by step to isolate and solve for the unknown values.
Step 3: Verify Your Results
After calculating the unknowns, double-check your work. Verify that your solution satisfies all the relationships and conditions presented in the problem. For example, if you calculated an angle, ensure that it complements adjacent angles to add up to 180 degrees.
By following these steps, you can approach each problem systematically and solve it with confidence.
Angles and Sides in Parallelograms
In geometry, understanding the relationships between angles and sides is key to solving problems involving specific quadrilaterals. These figures have unique rules that govern how their sides and angles interact. Recognizing these connections helps in determining missing values, such as the length of a side or the size of an angle, and can simplify complex geometric tasks.
Relationship Between Sides and Angles
In these shapes, there are several important relationships to consider:
- Opposite sides are equal in length and run parallel to one another.
- Adjacent angles are supplementary, meaning their sum equals 180 degrees.
- Opposite angles are congruent, meaning they are identical in size.
Example: Solving for Sides and Angles

Below is an example table showing how different values of sides and angles can be solved based on the relationships above:
| Given Information | What Can Be Determined |
|---|---|
| One angle is 70° | The adjacent angle is 110° (since 180° – 70° = 110°) |
| One side length is 5 cm | The opposite side is also 5 cm (since opposite sides are equal) |
| Two adjacent sides are equal | Both opposite sides will also be equal (parallel sides rule) |
By using these relationships, you can solve for unknown values and confirm the consistency of the shape’s properties.
Understanding Diagonals of Parallelograms
In geometry, the diagonals of specific quadrilaterals have important properties that play a key role in solving problems. These line segments, which connect opposite corners, offer valuable insights into the shape’s symmetry and structure. By understanding how the diagonals behave, you can uncover hidden relationships and calculate unknown values more easily.
Key Features of Diagonals
There are several key characteristics that define the diagonals in these shapes:
- Bisect Each Other: The diagonals always intersect at their midpoint, dividing each diagonal into two equal parts.
- Non-Perpendicular: Unlike rectangles or squares, the diagonals of these shapes do not meet at right angles.
- Symmetry: The intersection of the diagonals creates a point of symmetry, splitting the shape into two equal halves.
How Diagonals Help Solve Problems
By utilizing the properties of diagonals, you can solve for unknown angles or lengths. Here’s how to apply the key features:
- If you know the length of one diagonal, you can calculate the lengths of the two segments created by the intersection.
- In some cases, you can use the diagonals’ intersection point to find missing angles, especially when dealing with congruent triangles formed by the diagonals.
- Knowing that the diagonals bisect each other can also help in verifying the symmetry of a given shape or confirming that opposite sides are equal.
Understanding the role of diagonals in these shapes simplifies the problem-solving process and strengthens your geometric knowledge.
Common Mistakes in Parallelogram Questions
When solving geometry problems involving specific quadrilaterals, there are several common errors that can lead to incorrect answers. These mistakes often arise from misunderstanding key properties or overlooking important relationships between the sides, angles, and diagonals. By being aware of these pitfalls, you can improve your problem-solving skills and avoid errors that could derail your work.
Misunderstanding Side and Angle Relationships

One of the most frequent mistakes is assuming that all angles in these shapes are right angles or that adjacent sides are not equal. In reality, only opposite angles are congruent, and adjacent angles are supplementary. Here are some common errors:
- Assuming all angles are 90°: This is only true for rectangles, not all shapes of this type.
- Confusing adjacent and opposite sides: Only opposite sides are equal, not adjacent ones.
Incorrect Use of Diagonals
Another common mistake involves the properties of the diagonals. Many assume that the diagonals are perpendicular or that they are equal in length. However, this is not always the case. The following errors are typical:
- Misunderstanding diagonal intersection: While diagonals bisect each other, they do not necessarily divide the shape into two identical halves unless additional properties apply.
- Incorrect diagonal length assumptions: Diagonals are not always equal in length unless the shape is a rectangle or square.
Avoiding these mistakes involves careful attention to the relationships between the sides, angles, and diagonals. By reviewing these properties and applying them correctly, you’ll be able to solve problems with greater accuracy and confidence.
Visualizing Parallelogram Geometry
Understanding the geometry of certain quadrilaterals can be challenging without a clear visual representation. By visualizing these shapes, you can better grasp their properties and how different elements like angles, sides, and diagonals interact. A strong mental image of the structure allows for more efficient problem-solving and helps in recognizing key relationships when tackling geometric questions.
When visualizing, it is important to focus on the following aspects:
- Parallel Sides: The opposite sides of the shape always run parallel to each other. This basic property helps in understanding the overall symmetry and balance of the figure.
- Equal Angles: Opposite angles are congruent. Seeing this symmetry can simplify calculations involving angles and assist in determining unknown angle measures.
- Diagonal Intersection: The diagonals bisect each other at their midpoints. Recognizing how they divide the shape into smaller triangles can be especially useful when solving for unknown areas or angles.
Having a mental or physical diagram of the figure, with all the important features labeled, can greatly enhance your understanding and make it easier to apply mathematical concepts to find solutions. Visualizing the geometry of these shapes not only aids in solving problems but also deepens your overall understanding of geometric principles.
Properties of Opposite Sides and Angles

In the study of specific quadrilaterals, the relationship between opposite sides and angles plays a crucial role in understanding their structure. These figures exhibit distinct patterns that help identify and solve geometric problems. The key to mastering these shapes lies in recognizing how opposite elements behave consistently, regardless of the shape’s size or orientation.
For example, opposite sides of these shapes are always equal in length, which means that no matter the dimensions of the figure, each pair of opposite sides will match in measurement. This fundamental property provides a strong basis for calculations involving side lengths and allows for comparisons between different quadrilaterals.
Similarly, opposite angles are congruent, meaning that they are always equal. This property simplifies the process of finding unknown angles, as knowing one angle in a pair directly reveals the measure of the other. Whether the shape is tilted or rotated, this relationship remains constant and is a powerful tool in problem-solving.
Key Points:
- Opposite sides: Always congruent and parallel to each other, ensuring symmetry.
- Opposite angles: Always equal, providing valuable information for angle-related calculations.
By understanding these essential characteristics, solving problems involving such quadrilaterals becomes more straightforward. The consistency of opposite sides and angles allows for the application of algebraic and geometric methods to find missing measurements or verify given information.
Real-World Applications of Parallelograms
The concepts of geometry are not just confined to the classroom; they play a crucial role in various real-life scenarios. The shapes we study, particularly certain types of quadrilaterals, can be found in everyday objects, architectural designs, and even engineering projects. Understanding the properties of these shapes can help solve practical problems and optimize designs in numerous fields.
One common example is in construction and design, where these geometric figures are used in creating stable structures. Beams, roofs, and windows often rely on the characteristics of these shapes to maintain balance and durability. For instance, the opposite sides being equal in length ensures even distribution of forces, which is vital in the design of load-bearing structures.
Applications in Engineering and Architecture:
- Building Frames: The properties of opposite sides being parallel and equal make these shapes ideal for creating strong, symmetrical frames for buildings and bridges.
- Roof Design: The geometric structure helps ensure that force and weight are evenly distributed, particularly in slanted or gabled roofs.
- Window Frames: These shapes are commonly used in window designs, where stability and even pressure distribution are necessary.
In addition to architecture, these shapes also appear in various everyday objects, such as tiles, carpets, and artwork. Their predictable characteristics make them easy to use in design, ensuring that materials fit together seamlessly and provide a visually balanced result.
By applying geometric principles to practical problems, engineers and designers can make informed decisions that improve both functionality and aesthetics in real-world applications.
Using Formulas in Parallelogram Problems
When solving geometry problems involving certain quadrilaterals, applying the right formulas can simplify complex calculations and provide quick solutions. These formulas are essential for finding various unknown quantities such as area, side lengths, and angles. By understanding the relationships between the sides and angles of these shapes, you can confidently apply formulas to solve problems accurately.
One of the most commonly used formulas is for calculating the area. The area of a figure like this can be determined by multiplying the length of one of its sides by the height, or the perpendicular distance between two opposite sides. This formula is effective because it accounts for the shape’s inherent symmetry and structure.
Key Formulas:
- Area Formula: Area = Base × Height – where the base is the length of one side and the height is the perpendicular distance between opposite sides.
- Perimeter Formula: Perimeter = 2 × (Base + Side) – used to find the total length around the figure.
- Angle Calculation: Use known angle relationships, such as opposite angles being equal, to calculate unknown angles.
In problems involving unknown side lengths or angles, these formulas allow for step-by-step solutions. By using the known dimensions of a shape, you can substitute values into the formulas to calculate missing parts. For example, if the height or one of the angles is given, you can use these details to solve for other unknown quantities using algebraic methods.
By mastering these formulas, students and professionals alike can confidently approach various geometric challenges, from basic classroom exercises to real-world engineering problems. Understanding how to apply these formulas ensures accurate results and a deeper understanding of geometric principles.
Exploring Parallelogram Symmetry
Symmetry plays a key role in understanding the structure and properties of geometric shapes. In certain quadrilaterals, symmetry provides insight into their balanced and orderly characteristics, helping to predict the behavior of their sides, angles, and diagonals. Recognizing the symmetry within these shapes is essential for solving geometric problems and understanding their behavior in real-world applications.
These shapes exhibit specific types of symmetry, particularly with regard to their opposite sides and angles. The symmetry is not just a visual or aesthetic feature but a fundamental property that governs how the shape behaves under transformations, such as reflection and rotation. Understanding these symmetrical relationships is crucial for geometric analysis and problem-solving.
Types of Symmetry:
- Reflection Symmetry: These shapes have a line of symmetry that divides them into two identical halves. If one half is folded over the other, they match perfectly.
- Rotational Symmetry: Some shapes can be rotated around a central point and still match their original position after a certain degree of rotation. This feature is particularly useful when dealing with designs that require repetitive patterns.
Symmetry in Action: When studying symmetry, it is important to consider how opposite sides are congruent and parallel, which leads to predictable and repeatable patterns. This symmetry is often utilized in architectural designs, where stability and balance are essential. By leveraging symmetry, engineers and designers can create more efficient and aesthetically pleasing structures.
Exploring the symmetry of these shapes helps develop a deeper understanding of their characteristics and applications. By recognizing and applying the principles of symmetry, one can solve problems more effectively and appreciate the inherent beauty of geometric designs.
Tips for Solving Parallelogram Worksheet
When tackling geometric problems involving specific quadrilaterals, understanding the key concepts and applying systematic approaches is crucial for success. Whether you’re working with a set of equations, angle measurements, or side lengths, having a solid strategy can help simplify even the most complex problems. This section offers practical advice to guide you through solving problems effectively and efficiently.
One of the most important tips is to break down each problem into smaller, more manageable steps. Start by identifying the given information and what you’re being asked to find. This helps to structure your thinking and ensures that you don’t overlook any essential details. Additionally, always keep the fundamental characteristics of the shape in mind, such as the relationships between opposite sides and angles, as they will often be key to finding the solution.
Step-by-Step Approach:
- Visualize the Shape: Drawing a diagram can significantly clarify the relationships between different parts of the shape. It also helps you spot any missing information that can be inferred from the given data.
- Use Known Formulas: Make sure you’re familiar with the formulas that apply to the shape’s area, perimeter, and other relevant properties. Using the right formula can save time and lead to quicker solutions.
- Check Units: Ensure all measurements are in the same unit. Converting units when necessary prevents errors in calculations and ensures accuracy in your final answer.
By staying organized and methodical, you can reduce the likelihood of errors and increase your efficiency in solving these problems. Always double-check your work, especially when working with angle measures or side lengths, as small mistakes can lead to incorrect results. With practice, you’ll find that solving these problems becomes more intuitive and less daunting.
Interactive Resources for Parallelogram Learning
In the digital age, there are many tools and platforms available that can help enhance your understanding of geometric concepts. Interactive resources are particularly valuable for engaging with complex shapes and their properties in a hands-on way. These tools allow learners to visualize, manipulate, and experiment with various geometric figures, making abstract ideas more concrete and easier to grasp.
Whether you’re a student trying to improve your understanding or a teacher looking to supplement your lessons, interactive resources can offer a dynamic learning experience. These tools range from online simulations to apps that allow for real-time problem-solving and instant feedback. By using them, learners can explore various scenarios, adjust dimensions, and observe how different changes affect the figure in real-time.
Recommended Interactive Tools:
- Geometry Software: Programs like GeoGebra allow users to draw shapes, measure angles, and explore the relationships between different geometric elements.
- Online Quizzes: Many websites offer quizzes with interactive problems that challenge users to apply their knowledge and receive immediate feedback on their solutions.
- Virtual Whiteboards: Tools like Jamboard or Miro can be used for collaborative problem-solving, allowing multiple users to work together in real time on geometric tasks.
By incorporating these resources into your study routine, you can deepen your understanding and improve your ability to solve geometric problems. The interactive nature of these tools makes learning both enjoyable and effective, ensuring that key concepts stick in your memory.
Challenges in Parallelogram Problem Solving
Solving geometric problems involving quadrilaterals can sometimes be tricky, even for those with a solid understanding of basic shapes. The challenges often arise when working with figures that have multiple properties and require a deeper analysis of their components. Identifying key relationships, applying the right formulas, and recognizing hidden symmetries can pose difficulties for learners and practitioners alike.
One of the main difficulties comes from understanding how different aspects of the shape relate to one another. For instance, the angles, sides, and diagonals all have specific properties that must be considered in conjunction. Additionally, visualizing these relationships and translating them into mathematical expressions can be a complex process that requires both critical thinking and spatial awareness.
Common Struggles in Problem Solving:
- Identifying Correct Formulae: Sometimes, choosing the right formula for area, perimeter, or angles can be confusing, especially when there are multiple ways to approach a problem.
- Misinterpreting the Given Data: Incorrectly understanding or missing key information from the problem, such as side lengths or angle measures, can lead to errors in the solution.
- Visualizing Relationships: The ability to clearly visualize the geometric relationships between sides, angles, and diagonals is crucial but can be challenging, especially for complex figures.
These challenges can be overcome with practice and a systematic approach. Developing a strong foundation in geometry and honing problem-solving skills are key steps toward becoming more confident and efficient when working with geometric figures.
How to Approach Parallelogram Proofs
Proving geometric statements about quadrilaterals can be a challenging but rewarding experience. A structured approach is key to successfully solving these problems, particularly when it comes to showing that certain relationships hold within a shape. Whether it’s proving that opposite sides are equal, angles are congruent, or diagonals bisect each other, the process involves logical steps and careful attention to detail. Understanding the inherent properties of the figure is essential before diving into the proof process.
When tackling a geometric proof, it’s important to follow a methodical approach. The first step is often to identify the given information and what needs to be proven. Then, you can build on this information step by step, applying relevant theorems and properties along the way. Using a combination of geometric reasoning and algebraic manipulation can often simplify complex problems and lead to the desired result.
Steps to Approach a Proof:
- Step 1: Identify the Given and the Required: Start by clearly understanding what information is provided and what you need to prove. This will guide your logical reasoning throughout the proof.
- Step 2: Use Known Properties: Apply known facts about geometric figures, such as the relationships between sides and angles, to set up your proof.
- Step 3: Logical Deduction: Use logical steps and theorems to build upon what has been established so far, showing how the given leads to the conclusion.
- Step 4: Conclude the Proof: Once all necessary steps have been demonstrated, restate your result clearly, showing that the proof is complete.
Example Proof Table:
| Step | Explanation | Justification |
|---|---|---|
| 1 | Identify the given and required | Clarify the information provided and what is needed to prove |
| 2 | Apply properties of angles and sides | Use known geometric theorems (e.g., opposite sides are equal, adjacent angles are supplementary) |
| 3 | Use logical steps to connect information | Make deductions based on geometric relationships, applying theorems as needed |
| 4 | Conclude the proof | Restate the result and ensure all steps are verified |
By carefully following these steps, you can systematically approach and complete geometric proofs. Practice and familiarity with the different properties of quadrilaterals will improve both your understanding and confidence in solving similar problems in the future.