Geometry Homework Worksheet Answers for Students

Mathematical exercises can often seem intimidating, but with the right strategies, anyone can improve their skills and solve even the most challenging tasks. The key is to break down complex problems into simpler steps, allowing for a clearer path to the solution. Whether you’re dealing with shapes, angles, or numerical relationships, a methodical approach makes all the difference.

Step-by-step guidance is crucial for understanding how to navigate through different types of problems. Learning how to apply rules effectively and use logical reasoning can lead to faster and more accurate results. Emphasizing clarity and precision at every stage is the best way to build confidence and mastery.

With the right resources, you can gradually sharpen your skills and develop a deeper understanding of the subject. Utilizing various study materials, practicing regularly, and checking your work will significantly boost your ability to tackle mathematical exercises with ease and efficiency.

Geometry Homework Worksheet Answers

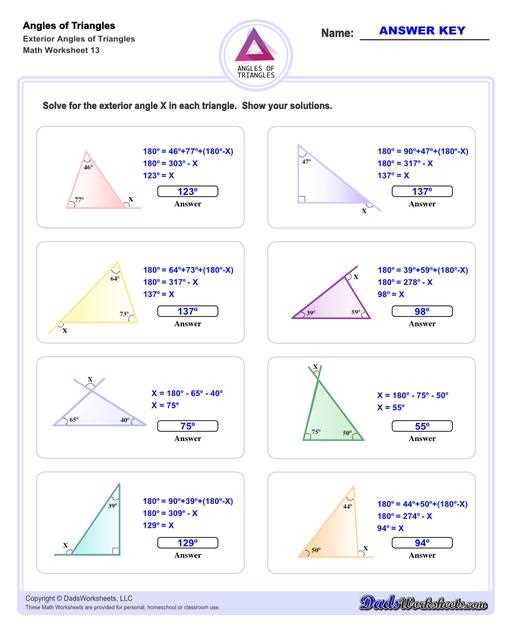
Solving mathematical problems requires a combination of practice, understanding key concepts, and using the right approach to reach the correct solution. With the right set of tools and a methodical process, tackling challenging questions becomes more manageable. By following a structured plan, you can effectively solve each problem and verify your work step by step.

When faced with exercises, it’s essential to:

Identify the problem’s core concept
Break the problem into smaller, more manageable parts
Apply relevant formulas or rules
Double-check calculations and logic

One of the most important steps in improving your skills is checking your results. Ensuring that every answer aligns with expected outcomes helps solidify your understanding and prevent errors. Additionally, if your answer is not correct, revisiting the steps will help pinpoint where things went wrong and improve your future performance.

By practicing consistently and approaching each task with confidence, you will gradually build proficiency and reduce the time spent on solving complex problems. Using available resources like guides and solutions for review can further enhance learning and accuracy.

Ultimately, mastering the techniques to solve these exercises not only boosts your grade but strengthens your analytical skills, which are crucial for tackling more advanced topics in the future.

Understanding Geometry Homework Problems

Mathematical exercises often present a series of challenges that require a clear understanding of both concepts and methods. These tasks typically involve applying formulas, recognizing patterns, and using logical reasoning to find solutions. The key to overcoming these challenges lies in breaking down each question into manageable parts, ensuring that every step follows a logical progression.

When approaching such problems, it’s important to first identify the main objective. Is the goal to find a specific value, prove a relationship, or demonstrate a particular concept? Understanding the task at hand will guide your approach and help you focus on the most relevant principles and techniques. Once the problem’s core idea is clear, you can begin to map out your solution.

Another critical aspect is recognizing common problem structures. Many tasks share similarities in their setup, so learning to identify these patterns can significantly reduce the time spent analyzing each question. With enough practice, you will start to notice recurring strategies that can be applied to a wide range of problems, making your approach more efficient.

Tips for Solving Geometry Questions

Successfully tackling mathematical problems requires a strategic approach. Whether dealing with shapes, angles, or spatial relationships, applying the right techniques can make a significant difference in your ability to solve each task efficiently and accurately. Below are several tips that will help streamline the process and improve your problem-solving skills.

Focus on Key Concepts

Understand the core principles before diving into the problem.
Familiarize yourself with the most common formulas and theorems.
Identify the type of problem and determine which concepts are most relevant.

Step-by-Step Problem Solving

Read the question carefully and identify what is being asked.
Sketch diagrams when applicable to visualize the problem better.
Work through each part of the problem one step at a time.
Double-check your work before finalizing your answer.

By mastering these strategies and practicing consistently, you’ll become more confident and efficient at solving complex problems in the future.

Common Geometry Homework Challenges

Mathematical problems often present various challenges that can make finding solutions difficult. These challenges stem from the need to grasp abstract concepts, apply specific rules, and accurately interpret information. Whether it’s understanding relationships between shapes or working with complex formulas, many students encounter obstacles that hinder their progress.

One of the most common difficulties is misinterpreting the problem. Often, it’s easy to overlook key details or make assumptions that lead to incorrect results. Additionally, some problems require the use of multiple concepts simultaneously, which can be overwhelming without a clear plan of action. Another frequent issue is making calculation errors, especially when working with measurements or geometric properties.

Finally, lack of practice can contribute to struggling with tasks. Without sufficient experience, it becomes harder to recognize patterns or quickly apply the right methods. Building confidence and improving skills takes time and repetition, but these challenges can be overcome with persistence and the right strategies.

How to Approach Geometry Word Problems

Word problems can often seem daunting due to their complex descriptions and the need to extract the relevant information. However, with a structured approach, these types of tasks become much more manageable. The key is to carefully analyze the problem, identify important data, and translate the verbal description into a mathematical model that can be worked through step by step.

Read and Understand the Problem

Start by reading the problem thoroughly, making sure to understand the context and what is being asked.
Highlight or underline key information such as numbers, relationships, and any conditions provided.
Look for clues that will indicate which concepts or formulas are needed.

Visualize and Organize the Information

Draw a diagram to represent the problem whenever possible. This helps clarify the relationships between different elements.
Label all known values and variables clearly, making sure nothing is overlooked.
Break down the problem into smaller, more manageable parts that can be solved step by step.

By following these strategies, you will be able to convert word problems into solvable tasks and improve your accuracy in finding solutions.

Step-by-Step Geometry Solutions

Breaking down complex problems into smaller, manageable steps is one of the most effective ways to ensure accuracy and clarity. By following a structured approach, you can solve even the most challenging tasks systematically. Each step serves as a checkpoint, allowing you to verify progress and make adjustments before moving forward.

To start, carefully read through the problem and identify the key elements that need to be solved. Once the main objective is clear, follow these general steps:

Step 1: Identify all given values and relationships in the problem. This could include measurements, angles, or other key data.
Step 2: Choose the appropriate formulas or rules that apply to the situation. Familiarity with these is essential for solving efficiently.
Step 3: Begin applying the formulas or methods step by step. Perform calculations carefully, showing all work to avoid mistakes.
Step 4: After completing the solution, double-check your results. Make sure the answer aligns with the given conditions and that all steps are logical and consistent.

Following a consistent, step-by-step process not only ensures correctness but also builds confidence, helping you approach similar tasks in the future with greater ease.

Key Geometry Concepts to Master

Mastering fundamental principles is essential for solving complex problems with confidence. A strong grasp of basic concepts serves as the foundation for tackling more advanced topics and enables you to recognize patterns and relationships in various tasks. Focused practice on core ideas allows you to approach different challenges with ease and accuracy.

Some of the most important concepts to understand include:

Shapes and Properties: Understanding the characteristics of different shapes, including triangles, quadrilaterals, and circles, is crucial for solving related problems.
Angles and Their Relationships: Knowing how to calculate and apply angles in different configurations is a key skill for many types of problems.
Perimeter, Area, and Volume: Calculating the perimeter of polygons, the area of two-dimensional shapes, and the volume of three-dimensional objects is fundamental to many exercises.
Coordinate Systems: Understanding how to work with points, lines, and equations on a coordinate plane is essential for graphing and solving spatial problems.
Transformations: Mastering concepts like translation, rotation, reflection, and dilation helps in solving problems involving symmetry and motion.

By gaining a deep understanding of these essential principles, you will be well-equipped to solve a wide range of problems efficiently and accurately.

Effective Geometry Study Techniques

Studying mathematical concepts effectively requires a combination of focus, structured methods, and consistent practice. The right study habits not only help you understand complex topics but also improve your ability to solve problems quickly and accurately. By incorporating various strategies into your routine, you can enhance both your understanding and performance.

Active Learning and Practice

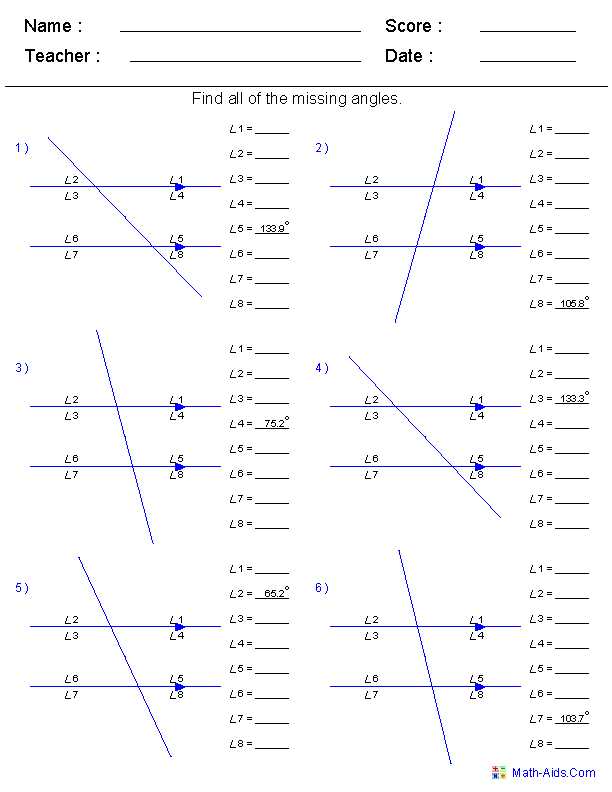
Work through problems regularly to reinforce concepts and improve problem-solving speed.
Break down complex problems into smaller steps and focus on one aspect at a time.
Seek out a variety of exercises to cover different types of problems and scenarios.

Utilizing Visual Aids and Resources

Create diagrams to visually represent problems and clarify relationships between elements.
Use online resources or textbooks that offer additional explanations, examples, and practice exercises.
Review solved problems to understand the methods used and apply them to new tasks.

By combining active practice with visual learning techniques, you can deepen your understanding and develop stronger skills for solving a wide range of mathematical challenges.

Geometry Formulas for Homework Success

Understanding and memorizing key formulas is crucial for solving many mathematical problems efficiently. Formulas provide a structured approach, enabling you to find the correct solutions quickly and accurately. Whether you are working with shapes, angles, or measurements, having the right formulas at your fingertips can significantly improve your problem-solving process.

Essential Formulas to Master

Area of a Circle: A = πr² – Useful for calculating the surface of circular shapes.
Perimeter of a Rectangle: P = 2(l + w) – Important for finding the boundary length of rectangles.
Volume of a Cube: V = s³ – Necessary for working with three-dimensional shapes.
Pythagorean Theorem: a² + b² = c² – Key for finding missing sides of right-angled triangles.
Surface Area of a Sphere: A = 4πr² – Used to calculate the surface area of spherical objects.

How to Apply Formulas Effectively

Always identify the type of problem to determine which formula to use.
Write down the formula before applying it to ensure all variables are accounted for.
Check your units and ensure they are consistent before calculating results.

By regularly practicing these formulas and applying them correctly, you’ll be able to solve problems with greater speed and confidence, making your study sessions more effective and efficient.

How to Check Geometry Answers

Verifying the correctness of your results is a critical step in solving mathematical problems. Ensuring that your calculations are accurate and that you’ve applied the right principles can help prevent mistakes and reinforce your understanding. There are several methods you can use to check your work and confirm that the solution is correct.

One effective way to check your solutions is to reverse the process. After obtaining an answer, work backward to see if the original conditions of the problem still hold true. Additionally, comparing your answer with different methods or cross-referencing with other problems can provide further validation.

Common Verification Techniques

Method	Description
Revisit the Steps	Go through the problem-solving process again, checking each calculation and ensuring the correct formulas were applied.
Estimate Results	If possible, estimate the expected range of the answer before performing detailed calculations to ensure it makes sense.
Cross-Check with Known Results	Compare your solution with similar problems or known formulas to see if the result aligns with what is expected.
Use a Calculator	For more complex calculations, using a calculator or a computational tool can help confirm accuracy.

By regularly applying these verification techniques, you can boost your confidence in your results and identify potential errors before finalizing your work.

Using Visual Aids in Geometry

Visual aids play a crucial role in understanding complex concepts, especially when dealing with spatial relationships and measurements. Diagrams, graphs, and drawings can help clarify abstract ideas, making them easier to grasp. When solving problems, having a visual representation allows you to see connections between elements, identify patterns, and guide your reasoning process.

One of the most effective ways to enhance your problem-solving ability is to draw diagrams. These illustrations can help you visualize the problem, making it easier to apply the right formulas or methods. Labeling key points, angles, and measurements in your diagrams ensures that all relevant information is accessible and visible, which reduces the risk of making mistakes.

Other useful visual tools include:

Graphs: Plotting data on a coordinate plane allows you to analyze relationships and trends more effectively.
Charts: Summarizing information in a chart can help organize complex data and highlight important connections.
Color Coding: Using colors to distinguish different elements or values can improve clarity and make it easier to track steps in a solution.

By incorporating visual aids into your study routine, you’ll find it easier to break down difficult problems and improve both understanding and accuracy in your work.

How to Avoid Common Mistakes

When solving mathematical problems, it’s easy to make small errors that can lead to incorrect results. These mistakes often occur due to oversight, rushing through the steps, or misapplying principles. Being mindful of common pitfalls can help you minimize these errors and improve the accuracy of your solutions.

Common Mistakes to Watch Out For

Skipping Steps: Rushing through the process without taking time to carefully complete each step can lead to missed details and incorrect answers.
Incorrect Formula Application: Misapplying formulas or using the wrong one for the given problem is a common mistake. Always double-check that you’re using the right equation.
Not Labeling Diagrams: Failing to label important points, angles, or lengths in diagrams can lead to confusion and incorrect reasoning.
Calculation Errors: Simple arithmetic mistakes, such as incorrect addition, subtraction, multiplication, or division, can easily skew results. Double-check calculations to avoid these errors.
Misinterpreting the Problem: Not fully understanding the problem’s requirements can lead to incorrect approaches. Read the question carefully to ensure you’re addressing the right issue.

Tips for Avoiding Mistakes

Review Each Step: Before moving on to the next part of the problem, pause and verify that each step is correct.
Double-Check Your Work: After completing the problem, go back over your calculations, diagrams, and formulas to ensure everything is accurate.
Take Your Time: Avoid rushing through the process. Allow yourself time to think critically and apply the correct methods.

By staying mindful of these common mistakes and following these strategies, you can improve both your efficiency and accuracy, leading to more consistent and reliable results.

Geometry Resources for Extra Help

When tackling mathematical challenges, sometimes additional resources are needed to clarify concepts and provide further explanations. Accessing the right tools and materials can make a significant difference in how well you understand and apply key principles. Whether through online platforms, textbooks, or tutoring services, there are numerous options available to help reinforce your knowledge and improve your problem-solving skills.

Online Resources

Khan Academy: Offers free video lessons and practice problems on a wide range of topics, including those related to shapes, measurements, and spatial reasoning.
Brilliant: An interactive platform providing courses and challenges that allow you to practice and apply various mathematical concepts in a hands-on way.
Wolfram Alpha: A computational tool that helps solve problems step-by-step and explains the solutions in detail.
Mathway: A tool for solving mathematical problems with step-by-step explanations that break down each calculation.

In-Person Help and Support

Tutoring Services: Many schools offer tutoring programs or access to peer tutors who can provide one-on-one assistance.
Study Groups: Collaborating with classmates or joining study groups can help you gain different perspectives and learn new strategies for solving problems.
Teacher Assistance: Don’t hesitate to ask your instructor for additional help or clarification on challenging topics.

By utilizing these resources, you can strengthen your understanding, clarify difficult concepts, and ensure you are fully prepared to tackle any problems that come your way.

Time Management for Geometry Homework

Effective time management is key to completing mathematical tasks efficiently and accurately. By organizing your study time and breaking down tasks into manageable parts, you can ensure that you cover all necessary material without feeling overwhelmed. The ability to allocate sufficient time for each problem, review your work, and stay focused is crucial for mastering concepts and performing well on assignments.

Strategies for Managing Your Time

Create a Schedule: Plan out your study sessions in advance. Set aside dedicated time blocks for working on problems to stay on track.
Break Tasks into Smaller Chunks: Divide large assignments into smaller, more manageable tasks. Focus on one part at a time to avoid feeling overwhelmed.
Set Time Limits: Allocate a specific amount of time for each problem or section. This prevents spending too much time on any one task and helps keep you moving forward.
Prioritize Difficult Tasks: Tackle the most challenging problems first, when your focus and energy are at their peak.
Avoid Multitasking: Concentrate on one task at a time to ensure you’re fully focused and performing each step correctly.

Maximizing Your Productivity

Use Breaks Wisely: Take short breaks between tasks to refresh your mind. This will help maintain focus and productivity over longer study sessions.
Review Your Work: After completing a problem, take a few minutes to review it before moving on to the next one to catch any potential mistakes.
Stay Organized: Keep your workspace tidy and your materials organized to minimize distractions and save time.

By applying these time management strategies, you can improve your productivity, reduce stress, and ensure that you’re well-prepared to tackle mathematical challenges effectively.

Breaking Down Geometry Proofs

Mathematical proofs can often seem daunting, but by breaking them down into smaller, logical steps, the process becomes more manageable. A proof involves demonstrating the truth of a statement using established facts, definitions, and logical reasoning. Understanding how to approach a proof systematically can make solving these problems both easier and more intuitive.

Key Steps in Constructing a Proof

To effectively break down a proof, it’s essential to follow a structured approach. The steps typically involve analyzing the given information, making logical deductions, and concluding with a clear statement that supports the original claim.

Step	Description
Identify Given Information	Begin by listing all the information provided in the problem. This includes known values, relationships, and any visual representations.
State What Needs to Be Proved	Clearly define the statement you need to prove. This helps to keep the goal in focus.
Apply Logical Reasoning	Use theorems, definitions, and properties to logically deduce intermediate steps that connect the given information to the statement you are proving.
Draw Conclusions	Summarize the logical steps to arrive at a final conclusion that confirms the validity of the statement.

Tips for Successfully Completing Proofs

Start with a Diagram: A well-labeled diagram can help visualize relationships between elements and provide insights into how to proceed.
Use Established Theorems: Leverage known theorems and properties, such as the Pythagorean Theorem or angle relationships, to strengthen your argument.
Work Backwards: If the proof seems complex, try working backward from the desired conclusion to uncover intermediate steps.
Be Thorough: Ensure that each step in the proof is backed by a valid reason, whether it’s a definition, postulate, or previously proven theorem.

By following these steps and tips, you’ll be able to approach proofs with confidence, systematically demonstrating the validity of each mathematical claim.

How Geometry Builds Problem-Solving Skills

Mathematics fosters critical thinking and strengthens problem-solving abilities by encouraging logical reasoning and pattern recognition. When engaging with tasks involving shapes, measurements, and spatial relationships, individuals are challenged to approach problems from multiple angles, refining their analytical skills. These exercises not only enhance understanding but also build the capacity to break down complex issues into manageable parts.

One of the primary ways mathematical concepts improve problem-solving skills is through the development of structured thinking. By learning to identify relevant information, make logical connections, and follow a step-by-step approach, individuals learn how to tackle unfamiliar challenges. The systematic nature of solving mathematical problems promotes the ability to think clearly and make sound decisions based on evidence and reasoning.

Furthermore, the discipline teaches perseverance and patience. As you encounter obstacles, you learn how to reassess the problem, consider alternative strategies, and remain persistent in seeking a solution. These skills extend beyond mathematics and can be applied to real-world scenarios, improving your ability to approach challenges in other fields with the same methodical approach.

Improving Homework Accuracy

Achieving accuracy in mathematical tasks requires attention to detail, careful application of principles, and a systematic approach to solving problems. The process of working through complex tasks involves multiple steps, and errors can easily slip in if one isn’t diligent. Developing habits that promote precision can help minimize mistakes and lead to more reliable solutions.

Key Strategies to Improve Accuracy

Strategy	Description
Understand the Problem Thoroughly	Before starting, take time to carefully read the problem and identify all the given information. Clarify what needs to be solved before proceeding.
Use Proper Notation	Consistently use correct symbols and terminology to avoid confusion. Proper labeling of elements, such as points, lines, and angles, helps keep your work organized and reduces errors.
Check Each Step	As you work through the solution, check your logic and calculations at each step. This will help catch any small mistakes before they accumulate.
Review Your Work	After completing a problem, review your solution from start to finish. Recheck the steps and verify your final result to ensure everything aligns correctly.

Additional Tips for Enhanced Precision

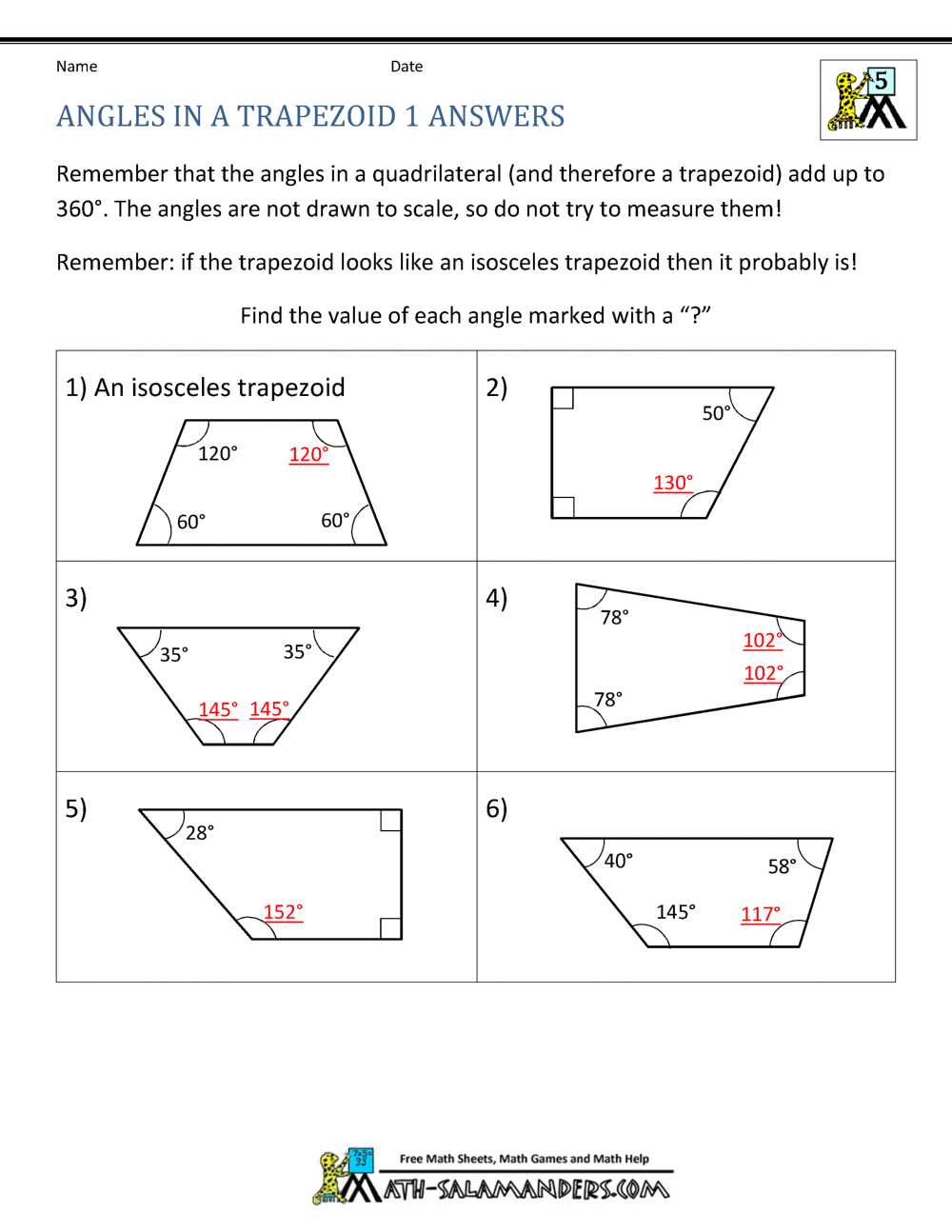
Double-Check Calculations: Recalculate your intermediate values to confirm that no arithmetic errors have been made.
Work Neatly: Clear and organized work reduces the likelihood of overlooking key steps or misinterpreting values.
Use Visual Aids: Diagrams and sketches can help visualize relationships between elements, making it easier to spot errors and guide your reasoning.

By adopting these practices, you can improve the accuracy of your mathematical solutions and gain a deeper understanding of the concepts you are working with.